Ευθύγραμμη
Ομαλά Μεταβαλλόμενη
Κίνηση
Μεγέθη
Θέση, μετατόπιση:
\vec{x}, \Delta\vec{x}
x⃗,Δx⃗
\vec{\upsilon }=\frac{\Delta \vec{x}}{\Delta t}
υ⃗=ΔtΔx⃗
Ταχύτητα:
Επιτάχυνση:
\vec{\alpha }=\frac{\Delta \vec{\upsilon}}{\Delta t}
α⃗=ΔtΔυ⃗
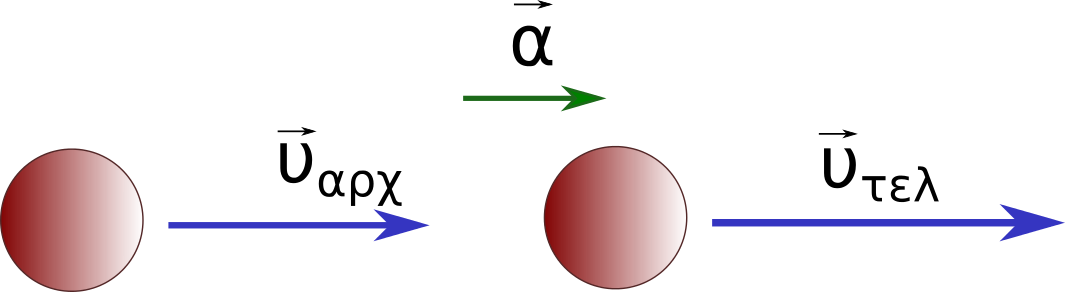
Κίνηση
Επιταχυνόμενη
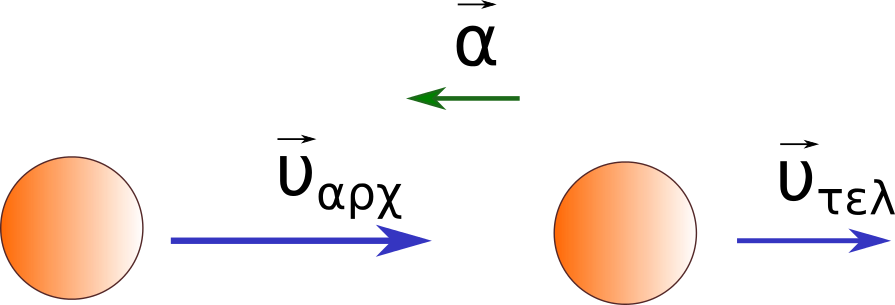
Επιβραδυνόμενη
Εξισώσεις Κίνησης
Μετατόπιση - χρόνος
\Delta x = \upsilon _{\alpha \rho \chi} \cdot \Delta t \pm{\frac{1}{2}\alpha \cdot \Delta t^2}
Δx=υαρχ⋅Δt±21α⋅Δt2
\upsilon =\upsilon _{\alpha \varrho \chi}\pm \alpha \cdot \Delta t
υ=υαϱχ±α⋅Δt
Ταχύτητα - χρόνος
Επιτάχυνση
\alpha = \sigma \tau \alpha \theta \varepsilon \rho \eta
α=σταθερη
Εφαρμογή
Ένα αυτοκίνητο κινείται με αρχικά με ταχύτητα μέτρου υαρχ = 20m/s σε ευθεία τροχιά. Την χρoνική στιγμή t = 0 αποκτάει επιβράδυνση μέτρου α = 4m/s.
- Γράψτε τις εξισώσεις μετατόπισης - χρόνου και ταχύτητας - χρόνου για την κίνηση του
- Υπολόγισε την ταχύτητα και την μετατόπισή του την χρονική στιγμή t = 2s
- Σε πόσο χρόνο η ταχύτητα του θα έχει γίνει υ = 2m/s
- Σε πόσο χρόνο η ταχύτητα του θα έχει σταματήσει;
- Πόση απόσταση χρειάζεται για να σταματήσει;
- Αν ένα εμπόδιο βρίσκεται σε απόσταση d= 55m, θα συγκρουστεί;
- Να φτιάξετε το διάγραμμα της ταχύτητας του αυτοκινήτου σε συνάρτηση με τον χρόνο.
- Υπολογίστε το εμβαδόν που περικλείεται από την γραφική παράσταση και τον άξονα των χρόνων; Τι εκφράζει αυτό το εμβαδόν;
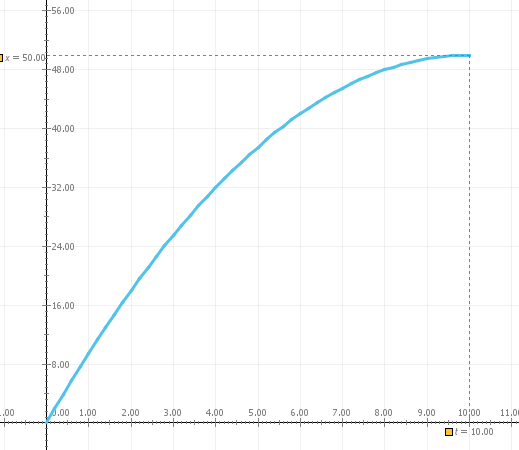
Επιταχυνόμενη
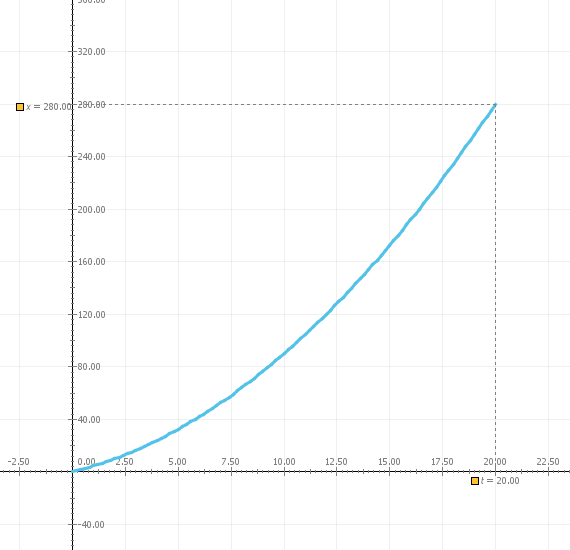
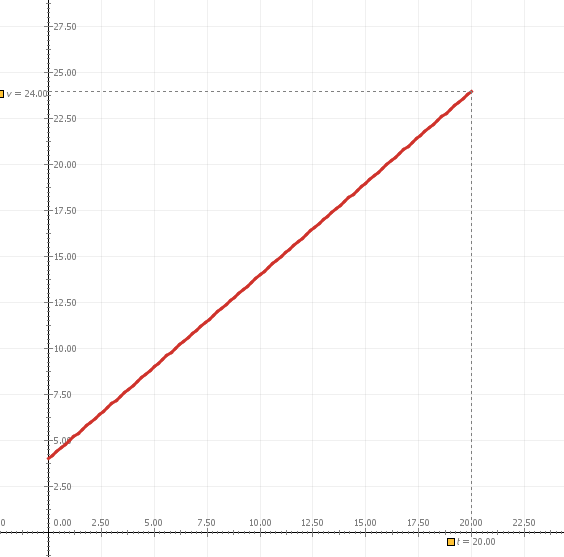
Διαγράμματα
Δx
t
t
υ
Κλίση: Ταχύτητα
Κλίση: Επιτάχυνση
Εμβαδόν: Μετατόπιση
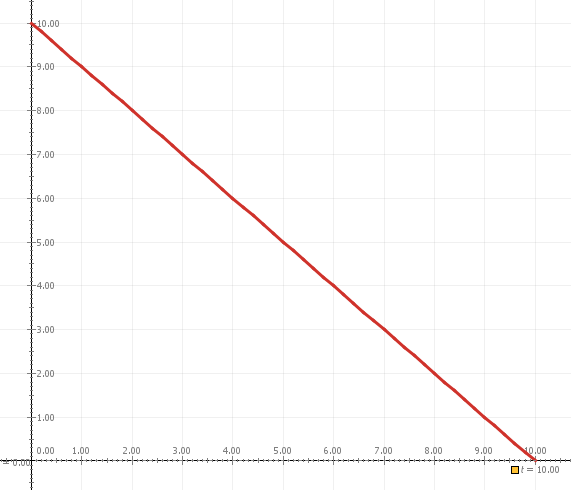
Επιβραδυνόμενη
Δx
t
t
υ