Διαγράμματα στην ευθύγραμμη

ομαλά μεταβαλλόμενη κίνηση

Tαχύτητα  σε συνάρτηση με τον χρόνο...

\upsilon - t

...όταν η ταχύτητα αλλάζει, με σταθερό ρυθμό...

  • το αντικείμενο κινείται όλο και πιο γρήγορα (επιταχυνόμενη)
  • ή όλο και πιο αργά (επιβραδυνόμενη)

 

  • όσο αλλάζει η ταχύτητα στο πρώτο δευτερόλεπτο, τόσο αλλάζει και στο δεύτερο, και στο τρίτο κ.λ.π.  
\upsilon
t

Η κλίση ισούται με:

 

 

 

\alpha = \frac{\Delta \upsilon }{\Delta t}
\Delta \upsilon
\Delta t

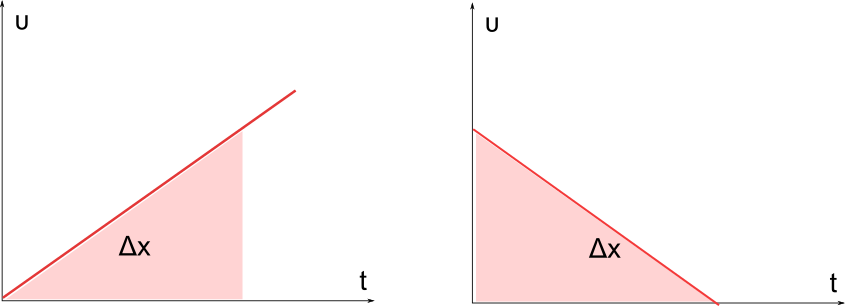
Η γραφική παράσταση της ταχύτητας, είναι ευθεία

άρα η κλίση το διάγραμμα υ-t, δίνει την επιτάχυνση

 

Το εμβαδόν της γραφικής παράστασης, δίνει την μετατόπιση του αντικειμένου

\Delta x=v_{\alpha \rho \chi} \cdot \Delta t+\frac{1}{2}\alpha \cdot \Delta t^2

Εφαρμογή

Μία μοτοσικλέτα αρχίζει να κινείται ευθύγραμμα,  με σταθερή  επιτάχυνση μέτρου                      .

A

  • Πόση είναι η ταχύτητα της την χρονική στιγμή t1 = 0;
  • Πόση είναι η ταχύτητα του την χρονική στιγμή t2 = 1s;
  • Πόση είναι η ταχύτητα του την χρονική στιγμή t3 = 2s;

B

  • Φτιάξε σε αριθμημένους άξονες την γραφική παράσταση της ταχύτητας της μοτοσικλέτας συναρτήσει του χρόνου  

 

 

\alpha =2m/s^2

Η επιτάχυνση παραμένει σταθερή:

  • ...δηλ., όποια στιγμή και αν την μετρήσουμε,  θα είναι η ίδια...

 

  • ... η αλλιώς:  Η ταχύτητα αλλάζει σε κάθε δευτερόλεπτο κατά το ίδιο ποσό

Η θέση του αντικειμένου σαν συνάρτηση του χρόνου

...μετράμε την απόσταση του από την θέση που βρισκόταν την χρονική στιγμή t=0

Αν η ταχύτητα αυξάνεται (επιταχυνόμενη κίνηση):

  • Σε ίσες χρονικές διάρκειες διανύει όλο και μεγαλύτερες αποστάσεις (αφού, "τρέχει πιο γρήγορα"...)
x=v_{\alpha \rho \chi} \cdot \Delta t+\frac{1}{2}\alpha \cdot \Delta t^2
x
\Delta t
\alpha

Εξίσωση:

 

 

   

         η απόσταση από την αρχική θέση,

         η ταχύτητα

           η χρονική διάρκεια της κίνησης που μελετάμε

 

Αν η ταχύτητα ελαττώνεται (επιβραδυνόμενη κίνηση):

  • Σε ίσες χρονικές διάρκειες διανύει όλο και μικρότερες αποστάσεις (αφού, "πάει πιο αργά"...)
x=v_{\alpha \rho \chi} \cdot \Delta t-\frac{1}{2}\alpha \cdot \Delta t^2

Εξίσωση

x
\Delta t
\alpha

 

 

 

   

         η απόσταση από την αρχική θέση,

         η ταχύτητα

         η χρονική διάρκεια της κίνησης που μελετάμε

 

\color{DarkBlue}x
\color{DarkBlue}t

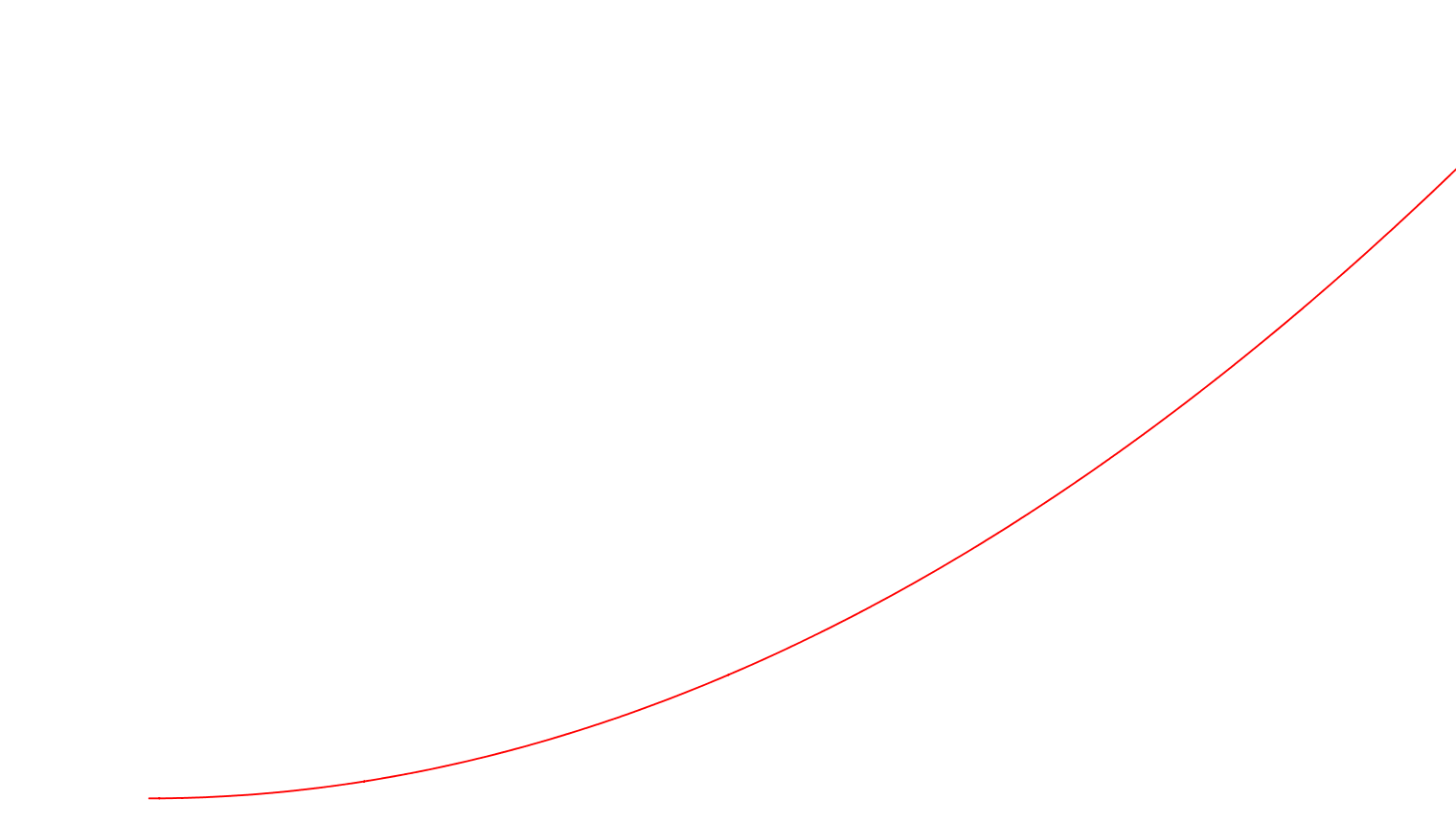
στην επιταχυνόμενη, οι αποστάσεις που διανύονται, είναι όλο και πιο μεγάλες

\color{DarkBlue}x
\color{DarkBlue}t

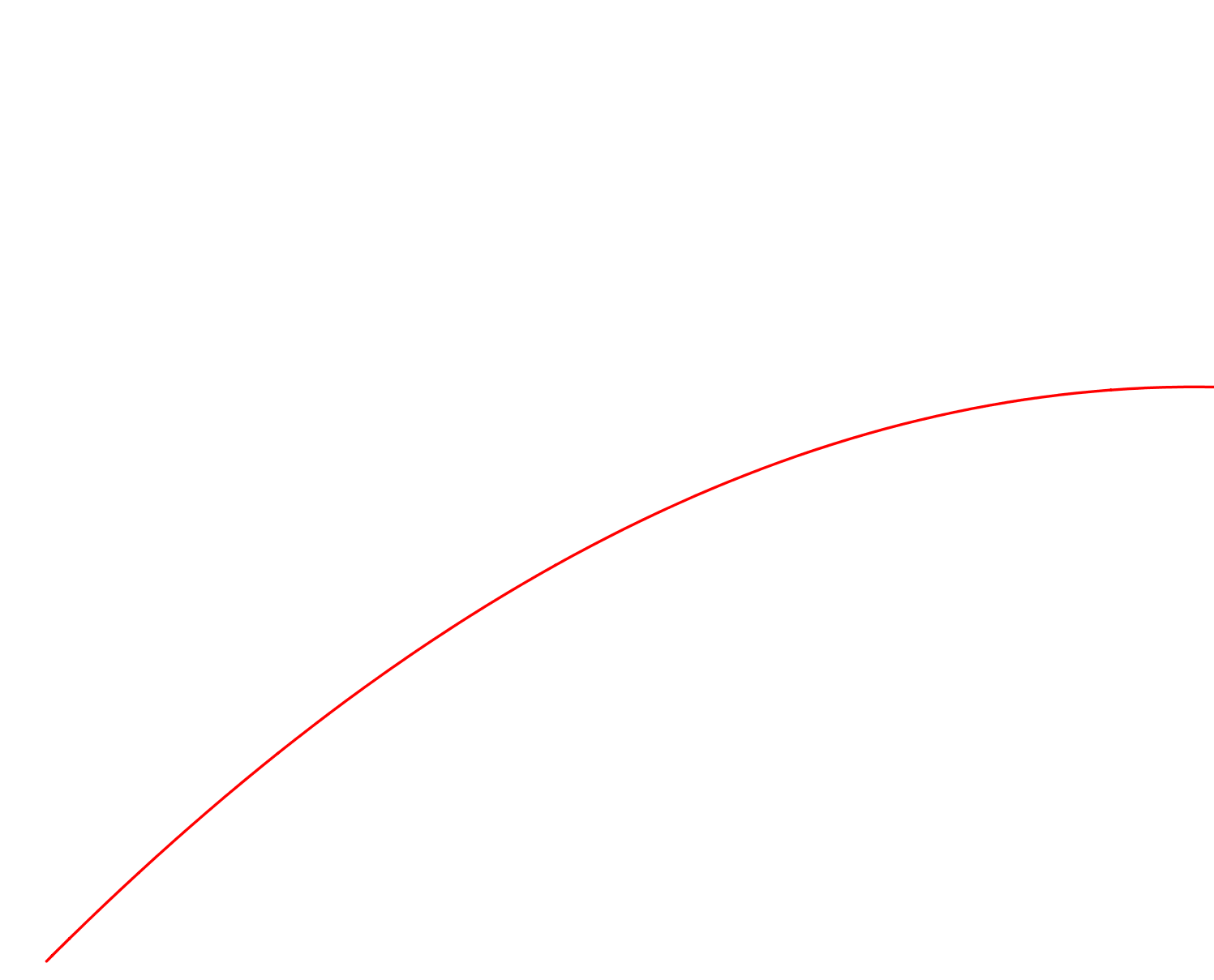
στην επιβραδυνόμενη, οι αποστάσεις που διανύονται, είναι όλο και πιο μικρές

  • Η γραφική παράσταση θα είναι ίδια με αυτήν της εξίσωσης "δεύτερου βαθμού" ("παραβολή")

Εφαρμογή

Για την μοτοσικλέτα του προηγούμενου παραδείγματος (                  ):


A

Θεωρώντας αρχική θέση την x = 0, υπολόγισε την θέση της τις χρονικές στιγμές t0=0s, t1=2s, t2=4s.


B

Σχεδίασε σε αριθμημένους άξονες το διάγραμμα επιτάχυνσης χρόνου (α-t)

Γ

Σχεδίασε σε αριθμημένους άξονες το διάγραμμα θέσης χρόνου (x-t)

\alpha = 2 m/s^2
Made with Slides.com