Введение в теорию экстремального значения
29.11.2024 - 06.12.2024, «Институт "Вега"»
CTO фонда алгоритмической торговли "Powerhouse"
Ранее:
- глава IT программы 200 тысяч геномов ФМБА
- архитектор АС СПОД в Сбере
- тимлид разработки в стартапе-единороге BostonGene
- разработчик и сотрудник ряда НИИ в России и Европе
- выпускник ФББ МГУ и лаборатории математических методов в биологии
О себе:
Лекция 1
1. Гаусс и не-Гаусс
2. Центральная предельная теорема
3. Экстремальная теорема и обобщенное EVD
4. EVD type I: распределение Гумбеля, закон двойного логарифма при экспоненциальном износе
5. EVD type II: распределение Фреше как распределения максимума из Парето
6. Пример Гнеденко и получение Гумбеля как максимума из распределения с ограниченной областью определения
7. EVD type III: распределение Вейбулла из распределений с толстыми хвостами и ограниченной областью определения
8. Формулировка теоремы Фишера-Типпетта-Гнеденко
9. Как подойти к доказательству? Max-стабильность.
10. Домены притяжения распределений как классы эквивалентности
11. Лемма Хинчина и вспомогательная лемма
12. Формальное доказательство
13. Примеры распределений: кто к чему сходится и что не сходится ни к чему.
Лекция 2
15. Основные понятия из анализа выживаемости
16. Достаточные признаки сходимости фон Мизеса
17. Достаточный признак сходимости к Гумбелю
16. Достаточный признак сходимости к Вейбуллу
17. Достаточный признак сходимости к Фреше
18. Необходимые признаки сходимости
19. Теория Караматы о медленно и регулярно изменяющихся функциях
20. Примеры медленно изменяющейся функции
21. Схематически доказательство для II и III типов
22. Схематически доказательство для I типа
23. Вторая теорема Пикандса-Балкемы-де Гаана
24. Обобщенное распределение Парето
25. Здача оценки хвостового индекса или параметра shape
26. Пример: почему вы умрете, а голый землекоп - может, и нет; как устроен конец вашей жизни
27. Пример: полуэмпирическое Value-at-Risk
28. Пример: Каховская ГЭС и dykes в Голландии
29. Пример: BLAST и статистика Карлина-Альтшуля
Extreme Value Theory: наука о хвостах распределений
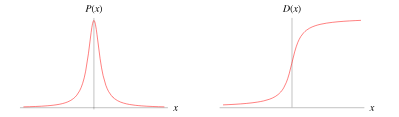
Есть ли среди слушателей кто-то, кому незнакомо данное распределение?
Extreme Value Theory: наука о хвостах распределений

Распределение Коши: \( f(x) = \frac{1}{1 + x^2} \)
Extreme Value Theory: наука о хвостах распределений
https://en.wikipedia.org/wiki/Witch_of_Agnesi
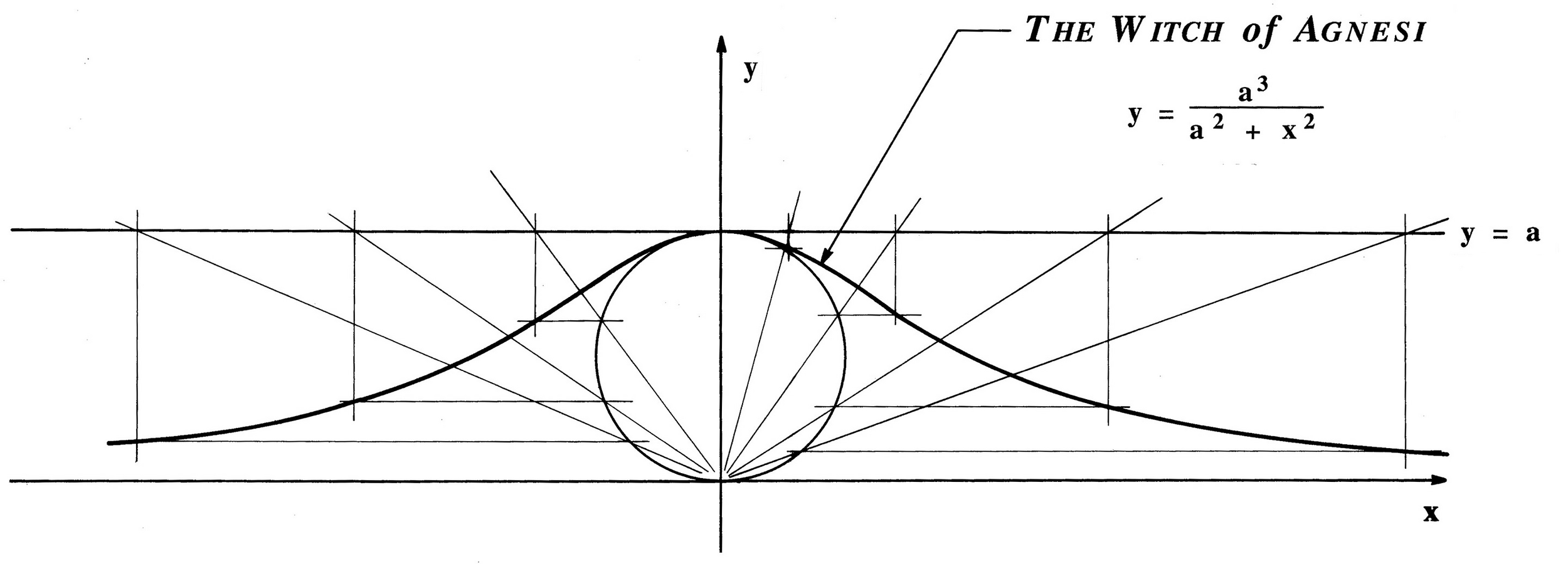
Локон/верзьера/ведьма Аньези
(la versiera di Agnesi / l’avversiera di Agnesi).


Maria Gaetana Agnesi (1718-1799)

John Colson (1680 -1760)

Extreme Value Theory: наука о хвостах распределений
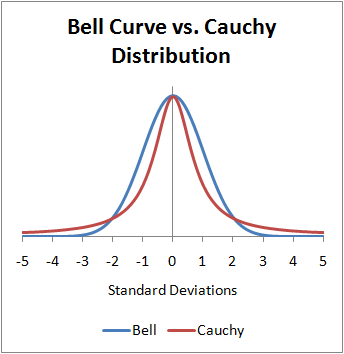

Extreme Value Theory: наука о хвостах распределений

Моменты не определены - посмотрим на матожидание:
Extreme Value Theory: наука о хвостах распределений

Вроде бы функция плотности
симметрична, поэтому матожидание равно 0?
Нет моментов - нет сходимости ЦПТ, ЗБЧ и т.д.
Но хотя A и B оба стремятся к бесконечности, они не обязаны делать это с равной скоростью. А тогда матожидание может принимать любое значение. Поэтому
от матожидания требуют абсолютной сходимости, а ее тут нет.
Extreme Value Theory: наука о хвостах распределений


Распределение Коши a.k.a. распределение
t-Стьюдента с 1 степенью свободы: \( f(x) = \frac{1}{1 + x^2} \)
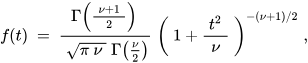
t-SNE CauchySNE
Extreme Value Theory: наука о хвостах распределений




Адмирал Кузнецов
Ляонин
Шаньдун
Викрамадитья
Центральная предельная теорема
Пусть \( \xi_1...\xi_n \) есть последовательность независимых одинаково распределённых случайных величин (далее н.о.р.с.в.), имеющих конечные матожидание \( \mu \) и дисперсию \( \sigma^2 \). Тогда \( \frac{S_n - n\mu}{\sqrt{n\sigma^2}} \xrightarrow{n \to \infty} \mathcal{N}(0, 1) \).
Центральная предельная теорема
"Душа" ЦПТ - в том, что гауссиана является собственной функцией для преобразования Фурье:
Центральная предельная теорема
Функция плотности суммы норсв - это свертка плотностей отдельных случайных величин:
Вспоминаем, что под преобразованием Фурье циклическая свертка переходит в адамарово произведение:
Центральная предельная теорема
Таким образом видим, что спектр функции плотности суммы есть адамарово произведение спектров плотностей отдельных функций плотностей. Раскладываем его по Тейлору, видим, что раз матожидание - нулевое, то и член первой степени нулевой, остается член второй степени.
Центральная предельная теорема
Значит, центральная часть спектра (для не безумно больших t) сходится к гауссиане, а поскольку хвосты распределения достаточно легкие, а гауссиана - собственная функция для Фурье, то и само распределение сходится к гауссиане при \( n \to \infty \).
Экстремальная теорема (Extreme Value Theorem, EVT)
Заменим сумму на максимум в формулировке ЦПТ. Можем ли мы что-то сказать о максимуме \( M_n \) н.о.р.с.в.?
Существует аналог центральной предельной теоремы, который называется теоремой об экстремальном значении.
"Центрированный" "нормированный" максимум невырожденных н.о.р.с.в. при достаточно большом \( n \) сходится к обобщенному распределению экстремального значения (Generalized Extreme Value Distribution, EVD):
Экстремальная теорема (Extreme Value Theorem, EVT)
На практике обобщенное распределение экстремального значения \( G_\gamma(x) = exp(-(1 + \gamma x)^{-\frac{1}{\gamma}}) \) принимает одну из трех форм:
- Распределение Гумбеля (EVD type I): \( G(x) = exp(-e^{-x}) \), \( \gamma = 0 \)
- Распределение Фреше (EVD type II): \( G(x) = exp(-(\frac{\lambda}{x})^{\frac{1}{\gamma}}) \), \( \gamma > 0 \)
- Распределение обратного Вейбулла (EVD type III): \( G(x) = exp(-(\frac{\lambda}{-x})^{ \frac{1}{\gamma} }) \), \( \gamma < 0 \)
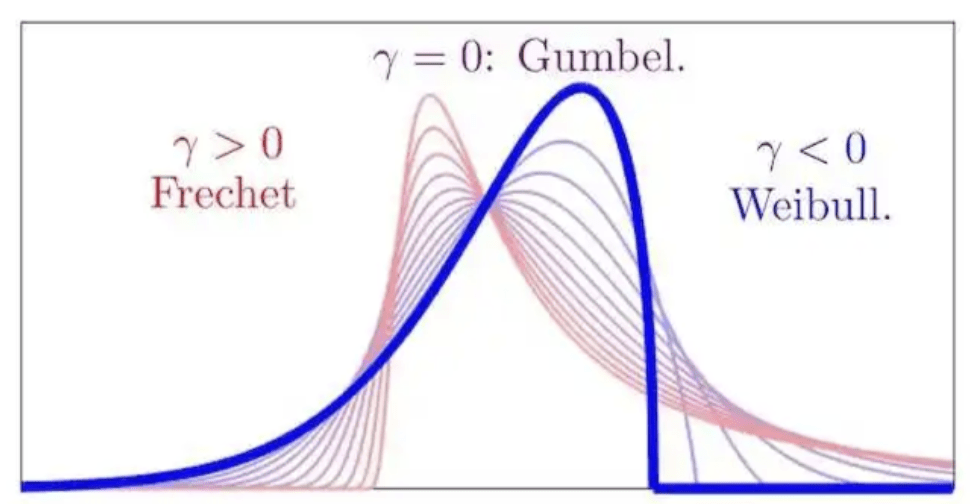
Распределение Гумбеля
(EVD type I) и закон двойного логарифма
Интуиция: телеги ломаются экспоненциально.
Какова вероятность, что хоть последняя из n сломается через x лет?
Распределение Гумбеля
(EVD type I) и закон двойного логарифма
Итак, в данном случае нам нужно вместо исходной случайной величины \( \xi \) рассмотреть "центрированную" случайную величину \( \eta = \xi - \ln n \), и вот она будет распределена по стандартному нормальному Гумбелю:
Распределение Гумбеля
(EVD type I) и закон двойного логарифма
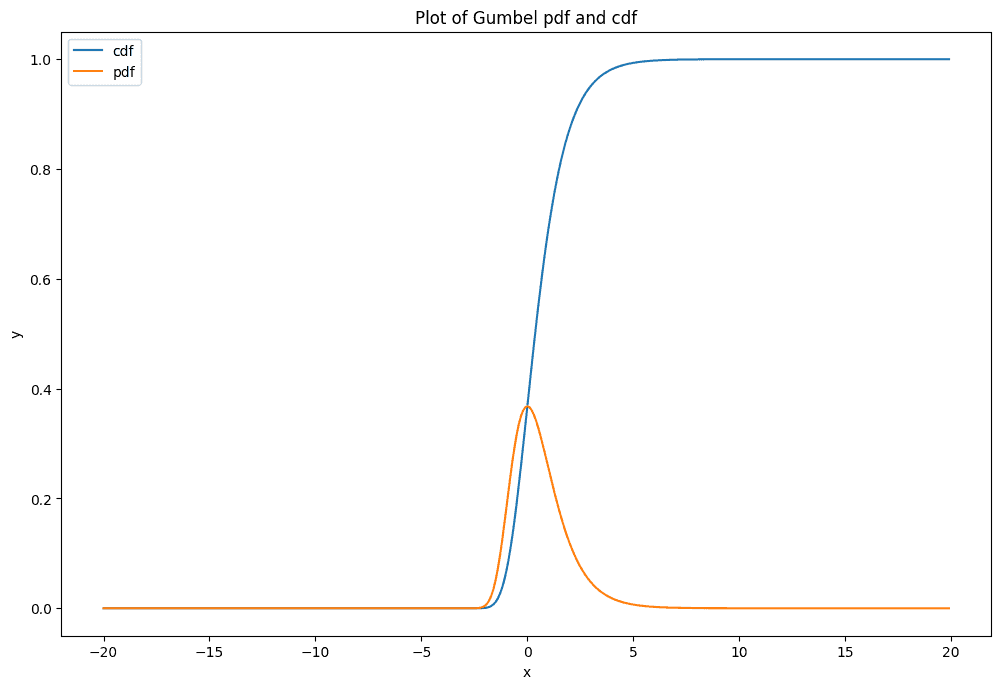
Распределение Гумбеля
(EVD type I) и закон двойного логарифма
Распределение Гумбеля получается из обобщенного распределения экстремального значения при параметре shape \( \gamma \) = 0.
Распределение Фреше
(EVD type II)
Интуиция:
В случае Гумбеля (тип I) исходное распределение имело легкий хвост (т.е. ограниченный сверху хвостом экспоненциального распределения). Что если распределение имеет тяжелый хвост (например, толстый гиперболический хвост вида 1/x)?
Disclaimer: ложные друзья переводчика
Я люблю начать называть хвосты распределений, которые ограничены сверху хвостами экспоненциального распределения, "субэкспоненциальными". Это НЕВЕРНО! Хвосты, ограниченные сверху хвостами экспоненциального распределения, называются легкими хвостами.
Я также люблю назвать тяжелые хвосты толстыми/жирными и наоборот. Это тоже НЕВЕРНО. Heavy tails - это все, что не легкие. Fat tails - это самый жесткий частный случай heavy tails - это хвосты, сходящиеся к гиперболам типа \( 1/x^\alpha \), "гиперболические" или "полиномиально-гиперболические".
Распределения с субэкспоненциальными хвостами - это частный случай тяжелых (heavy) хвостов, но все-таки не такой тяжелый случай, как толстые (fat).
https://en.wikipedia.org/wiki/Heavy-tailed_distribution
Распределение Фреше
(EVD type II)
Распределение в следующем уравнении не обязано быть экспоненциальным:
Что если, например, это распределение Парето:
Распределение Фреше
(EVD type II)
Распределение Парето описывает распределение капитала, числа подписчиков в соцсетях, величины трейдов на бирже и т.д.
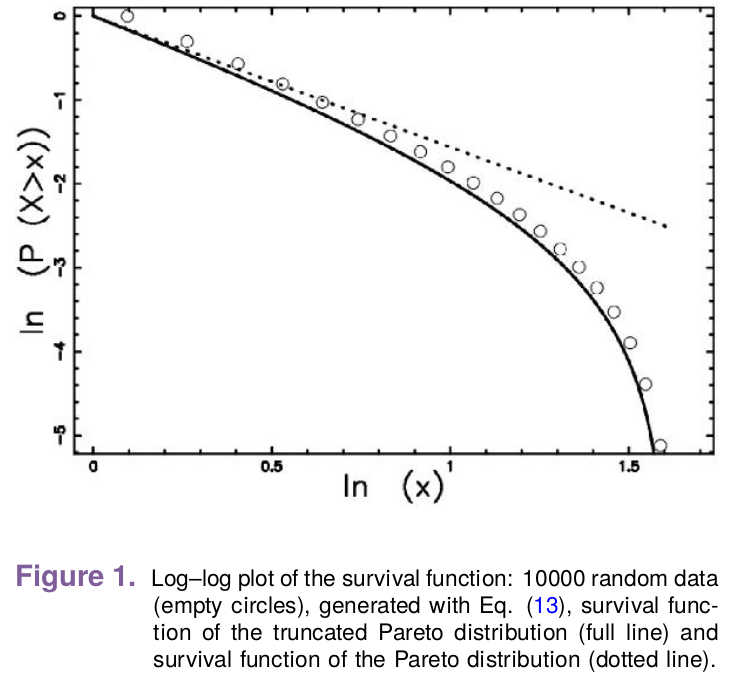
Распределение Фреше
(EVD type II)
Распределение Фреше
(EVD type II)
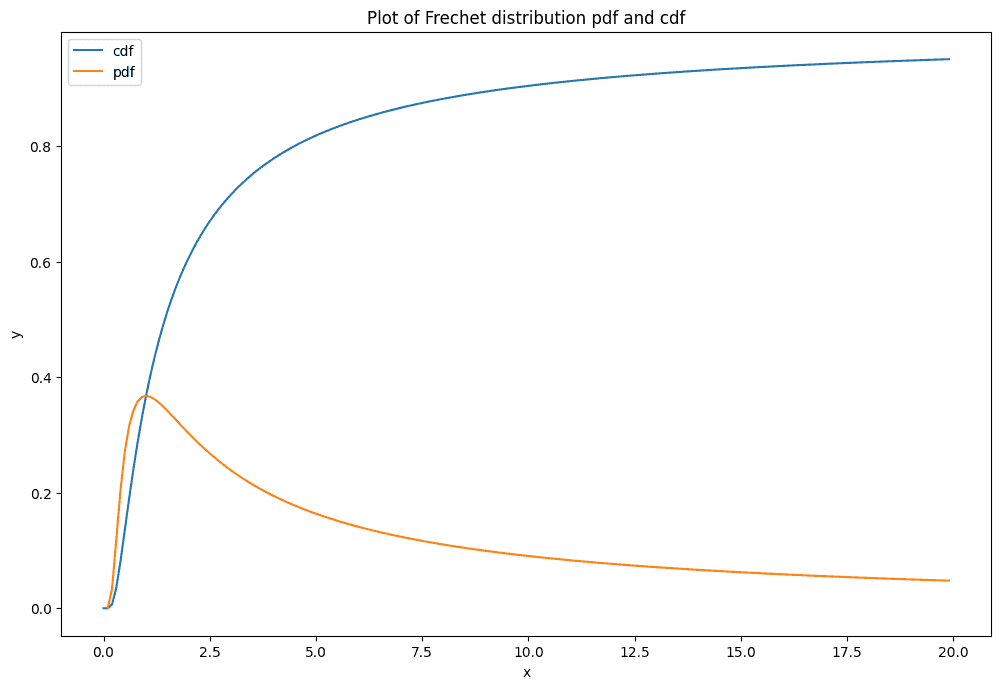
Распределение Фреше
(EVD type II)
Распределение Фреше получается из обобщенного распределения экстремального значения при параметре shape \( \gamma \) > 0.
Распределения с верхней границей
Мы можем рассмотреть распределения, аналогичные и распределению Гумбеля, и распределению Фреше,
но имеющие точный верхний предел, который обозначают \( x_F \) или \( \omega \). Их хвост мог быть легким или тяжелым. Что будет с их максимумом?
Трюк Гнеденко
В машинном обучении мы часто пользуемся трюком с сигмоидой/логитом, когда нам нужно превратить величину y ∈ [-∞, ∞] в величину x ∈ [0, 1].
Что если нам нужно превратить величину y ∈ [0, ∞] в величину x ∈ [0, 1]?
Рассмотрим пример Гнеденко (1943), который похож на половину трюка с сигмоидой.
Пример Гнеденко (1943)
Пример распределения с конечным хвостом \( x_F \) из работы Гнеденко (1943):
и наоборот, \( y - yx = x \), так что
Пример Гнеденко (1943)
Рассмотрим случайную величину \( \eta \) с экспоненицальным распределением:
Переобозначим \( \xi = \frac{\eta}{1 + \eta} \) и отыщем максимум \( \max \xi_n \) этих величин. Мы знаем, что нам нужно сдвинуть \( \xi \) на \( \ln n \), и нам нужно понять, к каким последствиям для \( \eta \) это приведет:
Пример Гнеденко (1943)
Нам нужно выразить \( a_n \xi + b_n \) через \( \eta - \eta_0 \), зная, что \( \xi = \frac{\eta}{1 + \eta} \).
Обозначим \( g(y) = \frac{y}{1+y} \). Мы знаем, что \( \xi = g(\eta) \).
Через ряд Тейлора или теорему о среднем значении на интервале \( \xi - \xi_0 = g(\eta) - g(\eta_0) = g'(\eta_0) (\eta - \eta_0) + O(\eta - \eta_o)^2 \).
Тогда \( \xi - \xi_0 = \frac{1}{(1 + \ln n)^2} (\eta - \eta_0) \) и \( (\xi - \xi_0) (1+\ln n)^2 \to \eta - \eta_0 \),
где \( \xi_0 = g(\eta_0) = \frac{\ln n}{1 + \ln n} \).
Итак, \( \max (\xi - \frac{\ln n}{1 + \ln n}) (1 + \ln n)^2 \sim e^{-e^{-x}} \).
Вспомним, как мы доказывали сходимость максимума экспоенциальный норсв к распределению Гумбеля:
\( p(\eta \le (y + \ln n)) = 1 - e^{-y - \ln n} = 1 - e^{-y}/n \)
Тут нам тоже нужно "центрировать" на логарифм.
Пример Гнеденко (1943)
Итак, мы нашли способ заменить нашу случайную
величину \( \xi \) на величину \( a_n \xi + b_n \), максимум которой явно сходится к распределению Гумбеля, где в данном случае:
и
Таким образом мы имеем распределение с верхней границей,
максимум из которого тоже сходится к типу I EVD (забегая вперед, скажем, что это так, потому что хвосты его все еще мажорируются экспонентой).
Распределение обратного Вейбулла (EVD type III)
В примере Гнеденко мы видели, что можно сплющить распределение так, что его правый край (бесконечность) перейдет в приближение к константе. Но если хвост при этом остался мажроируемым экспонентой, то распределение продолжит сходиться к I типу.
Распределение обратного Вейбулла (EVD type III)
А что будет, если теперь мы возмьем распределение с толстым гиперболическим хвостом, сходящееся ко II типу EVD, и его тоже "сплющим", так что его \( x_F = \infty \) перейдет в \( x_F = c \) ?
Оказывается, максимум такого распределения сойдется к распределению обратного Вейбулла (type III)
Распределение обратного Вейбулла (EVD type III)
\( F(x) = e^{-(\frac{-x}{\lambda})^{\gamma}} \), где x < 0 и 1 for \( x \ge 0 \).
Мы поймем, как прийти к нему позднее.
Распределение обратного Вейбулла (EVD type III)
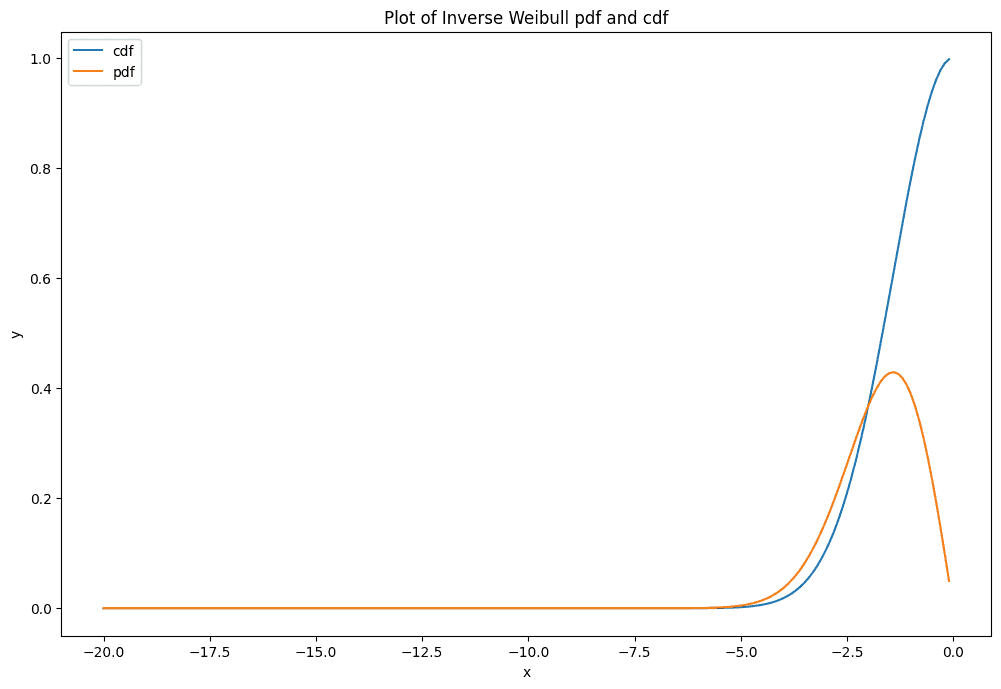
Распределение обратного Вейбулла (EVD type III)
Распределение Фреше получается из обобщенного распределения экстремального значения при параметре shape \( \gamma \) < 0.
Теорема Фишера-Типпета-Гнеденко a.k.a. первая теорема теории экстремального значения



Sir Ronald Aylmer Fisher
(1890-1962)
Борис Владимирович Гнеденко
(1912-1995)
Leonard Henry Caleb Tippett
(1902-1985)
Теорема Фишера-Типпета-Гнеденко a.k.a. первая теорема теории экстремального значения
Других распределений экстремального значения нет.
Если максимум "нормированных" "центрированных" н.о.р.с.в. из распределения вообще к чему-то сходится, он может сходиться только к Гумбелю, Фреше или обратному Вейбуллу.
Теорема Фишера-Типпета-Гнеденко a.k.a. первая теорема теории экстремального значения
Как же так?
Мы же видим общую логику, что \( (1 - F(x)/n)^{n} \xrightarrow{n \to \infty} e^{- F(x)} \) для любых F(x).
Например, кажется, что если подставить нормальное распределение \( f(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \), выйдет что-то вроде \( e^{-e^{-x^2/2}} \)?
А вот и нет...
Теорема Фишера-Типпета-Гнеденко a.k.a. первая теорема теории экстремального значения
\( F(x) = \frac{1}{\sqrt{2\pi}} \int \limits_{x \to \infty}^{\infty} e^{-\frac{t^2}{2}} dt \). Применяем интегрирование по частям:
Дальше вспоминаем, что нам-то нужно не просто F(x), а \( F(b_n x + a_n) \), и возможность выбора \( a_n, b_n \) дает нам достаточную свободу действия, чтобы мы смогли организовать сводимость \( \frac{e^{-(a_n x + b_n)^2/2}}{(a_n x +b_n)\sqrt{2\pi}}\sim \frac{e^{-x}}{n} \)
Теорема Фишера-Типпета-Гнеденко a.k.a. первая теорема теории экстремального значения
\( \frac{e^{-(a_nx+b_n)^2/2}}{(a_nx+b_n)\sqrt{2\pi}} = \frac{e^{-x^2/2b_n^2}e^{-x}}{x/b_n^2+1}\frac{e^{-b_n^2/2}}{b_n\sqrt{2\pi}} \)
Дальше - 2 манипуляции. Сначала выберем \( a_n = 1 / b_n \), и при этом \( b_n \to \infty \). Это позволяет раскрыть скобки и получить \( e^{-x} \):
Здесь удобно, что \( \frac{e^{-x^2/2b_n^2}e^{-x}}{x/b_n^2+1} \to e^{-x} \). Остается сконструировать конкретное \( b_n \) так, чтобы второй сомножитель \( \frac{e^{-b_n^2/2}}{b_n\sqrt{2\pi}} \to \frac{1}{n} \). Это достигается при выборе \( b_n = F^{-1}(1 - 1/n) \):
Итак, вопреки интуиции получаем: \( \frac{e^{-(a_n x + b_n)^2/2}}{(a_n x +b_n)\sqrt{2\pi}}\sim \frac{e^{-x}}{n} \)
Теорема Фишера-Типпета-Гнеденко
С какой стороны вообще подобраться к доказательству?
Теорема Фишера-Типпета-Гнеденко
Максимум-стабильные распределения и слабое/сильное звено
Максимум-стабильные распределения - это такие аналоги собственных векторов. Это распределения, для которых распределение максимума выборки из них сходится к ним самим. Например, максимум распределенных по Вейбуллу случайных величин после их "центрирования" и "нормирования" сойдется к Вейбулла.
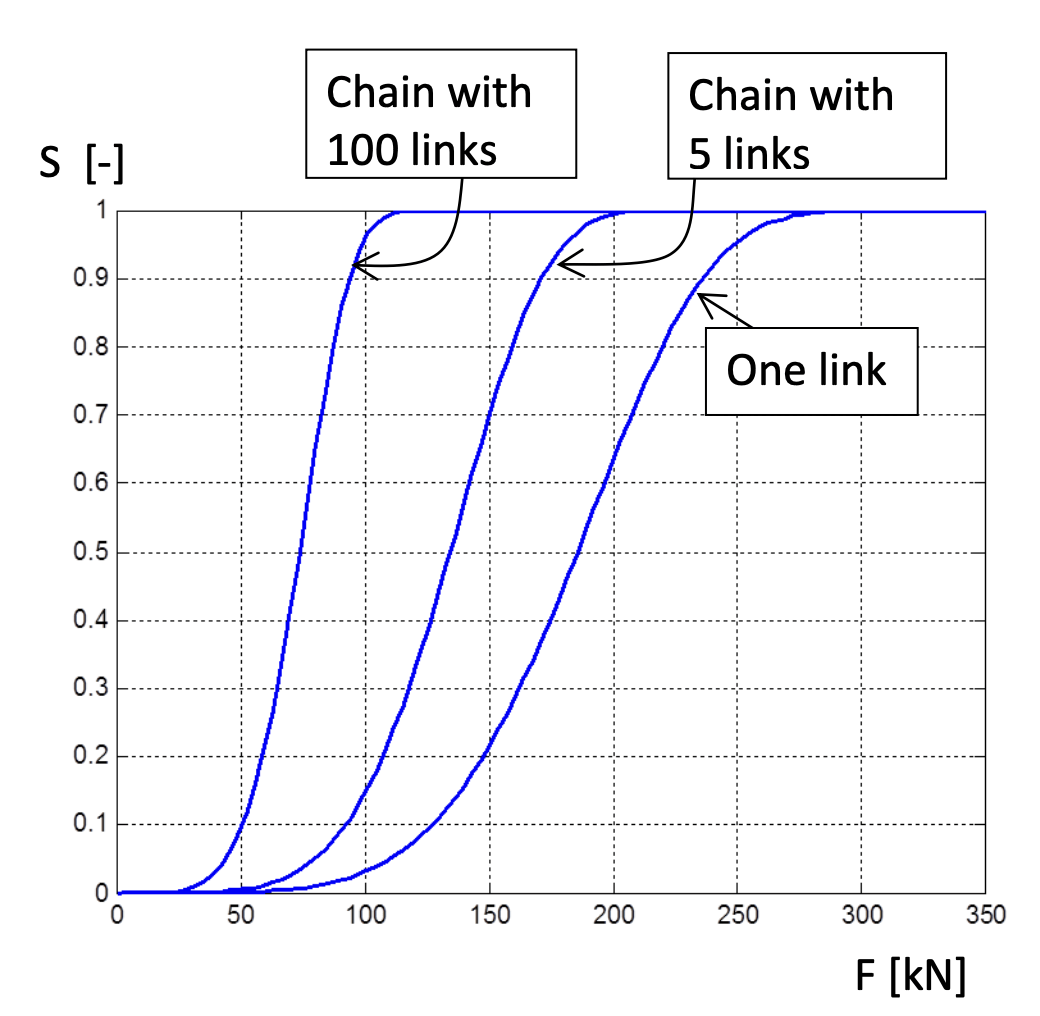
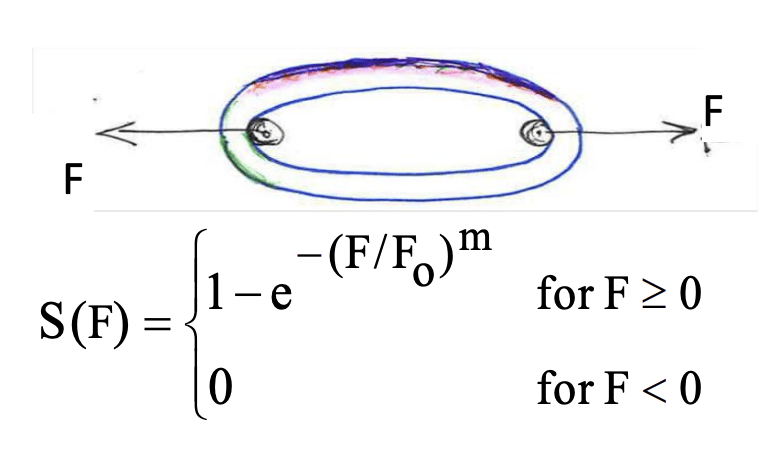


Теорема Фишера-Типпета-Гнеденко
Вспомогательные определения
Максимум-стабильная функция распределения (max-stable cumulative distribution function) - распределение G(x) называется максимум-стабильным, если для любых \( n \in 1..N \) существуют числовые ряды \( \{a_n\} \) и \( \{b_n\} \) такие, что для всех \( x \) соблюдается \( G(x) = G(a_n x + b_n) \).
Теорема Фишера-Типпета-Гнеденко
Вспомогательные определения
Как показать, что максимумы всех остальных распределений со временем свалятся в одно из максимум-стабильных распределений? Воспользуемся другим привычным инструментом - отношениями и классами эквивалентности. Например, все нечетные числа эквивалентны относительно операции деления по модулю 2, так как дают остаток 1 (например, 3∼5, где ∼ означает отношение эквивалентности при делении по модулю 2).
Мы покажем, что типы EVD образуют классы эквивалентности относительно операции максимума при n→∞ для норсв, и каждое распределение, максимум норсв из которого к чему-то сходится, в один из них попадает. Например, распределение Парето эквивалентно распределению Коши в отношении сходимости максимума n→∞норсв - обе сваливаются в распределение Фреше (тип II EVD).
Теорема Фишера-Типпета-Гнеденко
Вспомогательные определения
Область притяжения (Domain of attraction) - если F(x) - функция распределения, то F лежит в области притяжения распределения экстремального значения G (пишется \( F \in \mathcal{D}(G) \) ), если существуют числовые ряды \( \{a_n\} \) и \( \{b_n\} \) такие, что \( F^n(a_n x + b_n) \xrightarrow[n \to \infty]{w} G(x) \).
Тип сходимости (Type of convergence) - если \( G^*(x), G(x) \) - два распределения, то у них один тип сходимости, если для всех x существуют a, b, такие что \( G^*(ax + b) = G(x) \).
Лемма Хинчина
Александр Яковлевич Хинчин
(1894-1959)

Лемма Хинчина (закон Сходимости Типов)
Пусть дана функция распределения \( F_n \).
Пусть для этой функции распределения при \( n \to \infty \) существует пара рядов констант \( \{a_n\}, \{b_n\} \) такая, что максимум \( F(a_n x + b_n) \) сходится к G(x).
Пусть с другой стороны существует другая пара рядов констант \( \{\alpha_n\}, \{\beta_n\} \), такая что максимум последовательности \( F(\alpha_n x + \beta_n) \) сходится к другой функции H(x).
Тогда \( H(x) = G(Ax+B) \), где \( A = \frac{\alpha_n}{a_n}, B = \frac{\beta_n - b_n}{a_n} \).
Лемма Хинчина
Доказательство

Лемма о необходимом условии максимум-стабильности
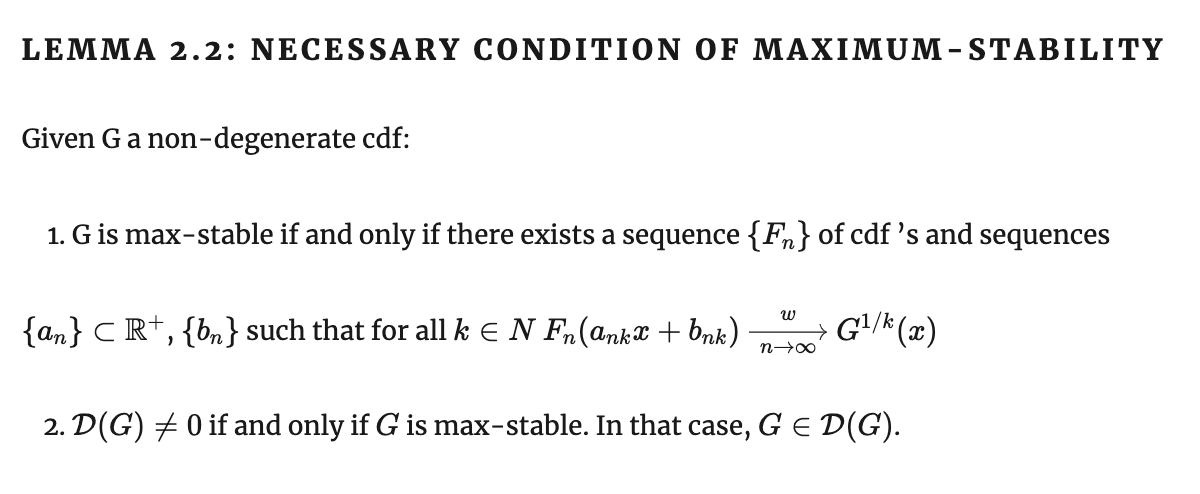
Лемма о необходимом условии максимум-стабильности

Лемма о необходимом условии максимум-стабильности

Лемма о необходимом условии максимум-стабильности
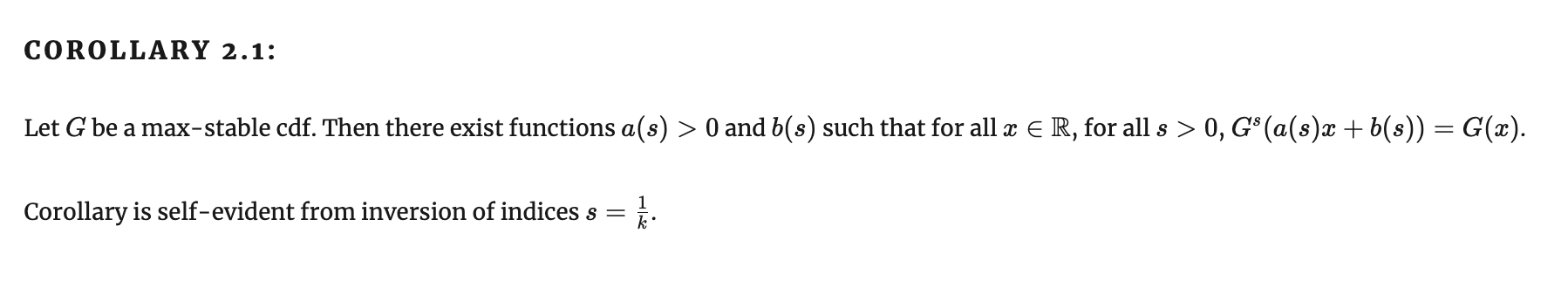
Теорема Фишера-Типпета-Гнеденко
Формулировка

Теорема Фишера-Типпета-Гнеденко
Доказательство

Теорема Фишера-Типпета-Гнеденко
Доказательство
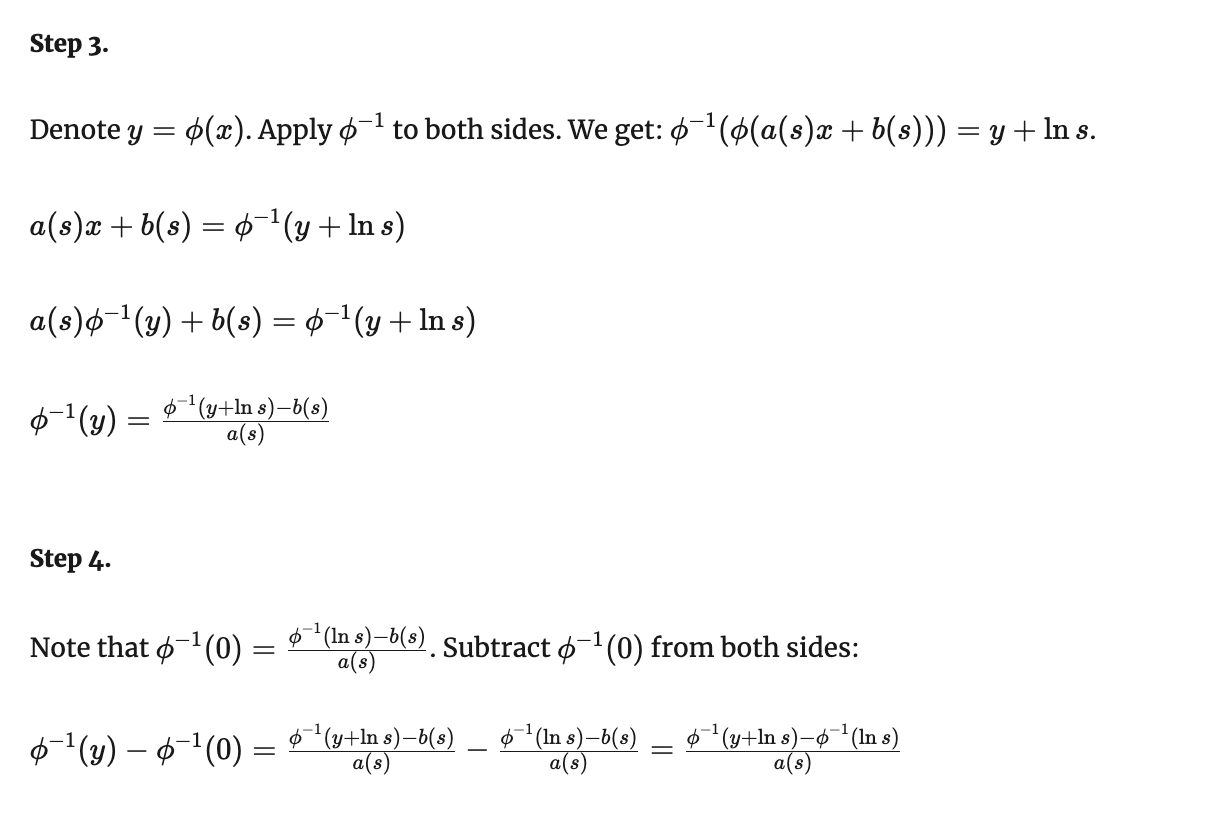
Теорема Фишера-Типпета-Гнеденко
Доказательство

Теорема Фишера-Типпета-Гнеденко
Доказательство

Теорема Фишера-Типпета-Гнеденко
Доказательство

Притяжение известных распределений к доменам EVD
EVD type I (Гумбель): экспоненциальное, нормальное, логнормальное, Вейбулл, Гумбель, Гомперц
EVD type II (Фреше): Парето, обобщенное Парето, Коши, Фреше, Стьюдент
EVD type III (обратный Вейбулл): равномерное, бета
Ни к одному: геометрическое, Пуассон
Лекция 1
1. Гаусс против Коши/Аньези
2. Центральная предельная теорема
3. Экстремальная теорема: постановка
4. Пример с жесткими дисками и экспоненциальным износом
5. Пример распределения Гумбеля, закон двойного логарифма, слабое звено в цепи
6. Распределение обратного Вейбулла как распределение с толстым хвостом
7. Пример Гнеденко как "половинка" трюка с сигмоидой и получение Фреше из Вейбулла
8. Тот же трюк, но с Гумбелем, который может иметь или не иметь точный верхний предел
9. Формулировка теоремы Фишера-Типпетта-Гнеденко
10. С какой стороны подойти к доказательству? Домены притяжения распределений как классы эквивалентности
11. Лемма Хинчина
12. Формальное доказательство
13. Примеры распределений, кто к чему сходится: Парето, Коши, Хи-квадрат, гамма...
Лекция 2
15. Основные понятия из анализа выживаемости
16. Достаточные признаки сходимости фон Мизеса
17. Достаточный признак сходимости к Гумбелю
16. Достаточный признак сходимости к Вейбуллу
17. Достаточный признак сходимости к Фреше
18. Необходимые признаки сходимости
19. Теория Караматы о медленно и регулярно изменяющихся функциях
20. Примеры медленно изменяющейся функции
21. Схематически доказательство для II и III типов
22. Схематически доказательство для I типа
23. Вторая теорема Пикандса-Балкемы-де Гаана
24. Обобщенное распределение Парето
25. Здача оценки хвостового индекса или параметра shape
26. Пример: почему вы умрете, а голый землекоп - может, и нет; как устроен конец вашей жизни
27. Пример: полуэмпирическое Value-at-Risk
28. Пример: Каховская ГЭС и dykes в Голландии
29. Пример: BLAST и статистика Карлина-Альтшуля
В предыдущих сериях...
- Теория экстремального значения - наука о хвостах распределений. Бывают распределения с легкими хвостами (которые убывают быстрее экспоненты) и тяжелыми хвостами (которые не легкие). Частный случай тяжелых хвостов - толстые/жирные хвосты, которые убывают как гипербора в какой-то степени.
- "Нормированный" и "центрированный" максимум из любого распределения может сходиться только к обобщенному распределению экстремального значения (Generalized EVD).
- Generalized EVD может реализовываться одним из 3 типов: распределением Гумбеля (type I), Фреше (type II) или обратного Вейбулла (type III).
- Теорема Фишера-Типпетта-Гнеденко говорит, что других типов нет.

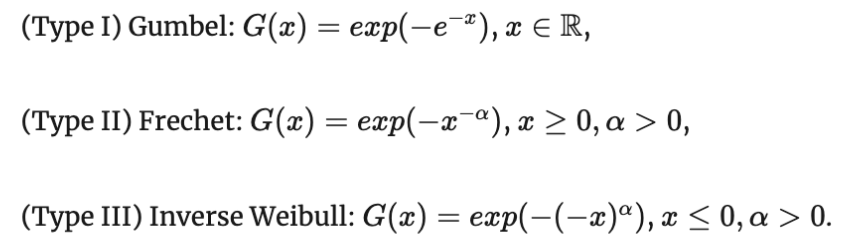
Достаточные признаки сходимости фон Мизеса
Как понять в общем случае, к какому типу EVD сходится данное распределение?
Richard von Mises (1883 - 1953)
Анализ выживаемости
Ключевые понятия
Функция выживаемости (Survival function) - обратная величина к функции распределения, \( S(x) = 1 - F(x) \). Доля тех, кто выживет к моменту времени x.
Интеграл функции выживаемости по времени равен средней
продолжительности жизни.
Анализ выживаемости
Ключевые понятия
Риск (hazard rate) - шанс умереть в момент времени x.
\( r(t) = \frac{f(t)}{1-F(t)} = \frac{f(t)}{S(t)} \). Пример: пусть в период с 80 лет до 81 года умирет \( f(t=80) = 4\% \) населения. Пусть до этого момента дожили \( S(t=80) = 40\% \) населения. Тогда hazard rate = 10%.
Накопленный риск (cumulative hazard rate) - "сколько раз вы бы должны были уже умереть к моменту x".
Соотношение между функцией выживаемости и накопленным риском:
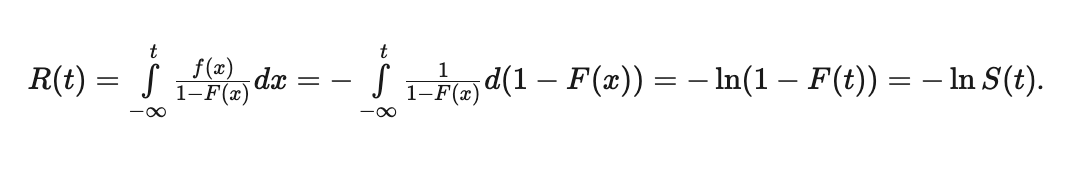
Анализ выживаемости
Ключевые понятия
Функция хвостового квантиля (tail quantile function):
\( \gamma(n) = \{ \inf t; F(t) \ge 1 - \frac{1}{n} \} = \{ \inf t; S(t) \le \frac{1}{n} \} \)
Например, \( \gamma(20) \) - это момент времени, когда осталось 5% популяции.
Признак фон Мизеса для EVD type II
Сходимость к распределению Фреше
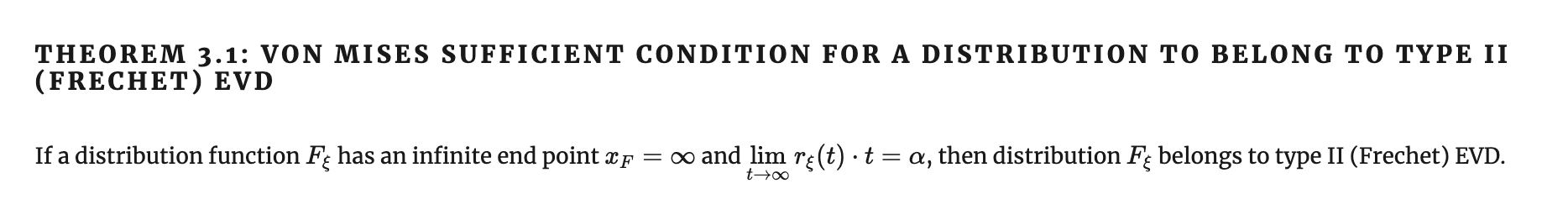
Признак фон Мизеса для EVD type II
Сходимость к распределению Фреше

Признак фон Мизеса для EVD type II
Сходимость к распределению Фреше

Признак фон Мизеса для EVD type II
Сходимость к распределению Фреше
Ко второму типу сходятся распределения, для которых риск смерти гиперболически падает со временем.
Например, такое поведение характерно
для идей, мемов, юмористических шоу. Смотрите эффект Линди - матожидание продолжительности жизни в момент времени \( t \) шоу равно его нынешнему возрасту \( t \).
Признак фон Мизеса для EVD type III
Сходимость к распределению обратного Вейбулла
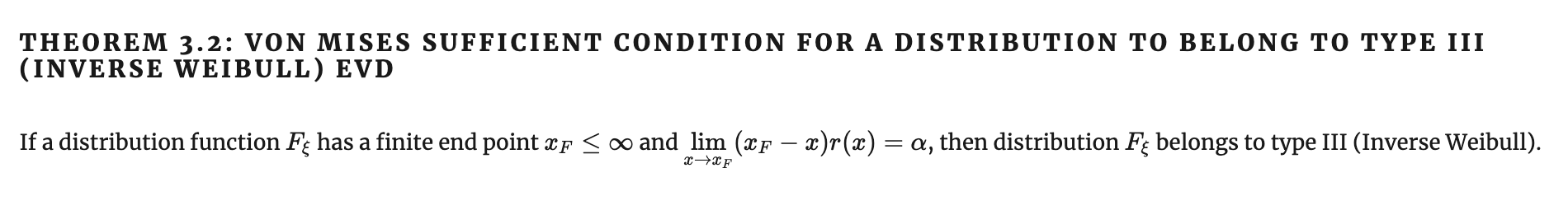
Признак фон Мизеса для EVD type III
Сходимость к распределению обратного Вейбулла

Признак фон Мизеса для EVD type III
Сходимость к распределению обратного Вейбулла
Попросту говоря, преобразованием координат мы растягиваем распределение, переносим его правый край \( x_F \) из конечной точки на бесконечность, а после этого применяем критерий для второго типа, сведя таким образом задачу к предыдущей.
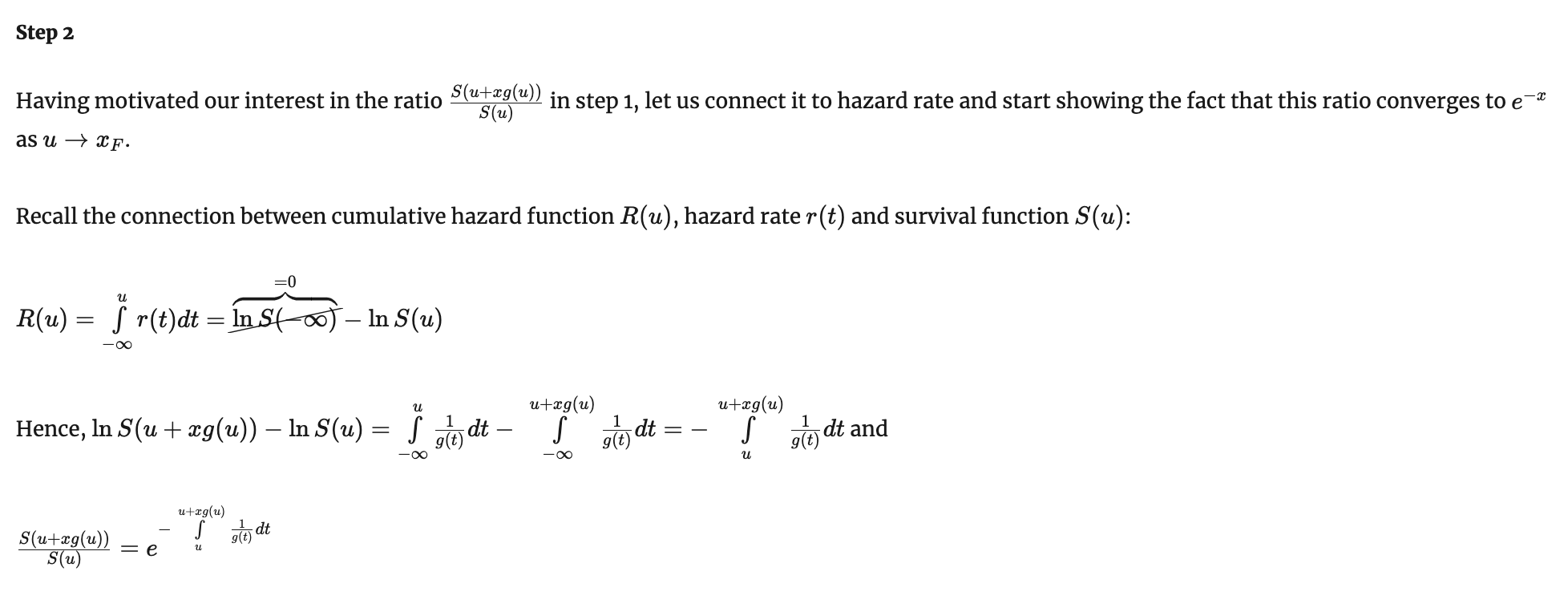
Признак фон Мизеса для EVD type I

Признак фон Мизеса для EVD type I

Признак фон Мизеса для EVD type I
Признак фон Мизеса для EVD type I

Признак фон Мизеса для EVD type I

Обобщенный признак фон Мизеса для EVD type I
Функция фон Мизеса и вспомогательная функция
Два инструмента, которые понадобятся, чтобы обобщить признаки фон Мизеса и перейти от них к необходимым и достаточным признакам сходимости распределения к одному из типов EVD.
Обобщенный признак фон Мизеса для EVD type I

Обобщенный признак фон Мизеса для EVD type I

Функция фон Мизеса нужна, чтобы доказать, что максимум ступенчатых распределений вроде геометрического или Пуассона не сходится ни к какому типу Generalized EVD.
Необходимые и достаточные признаки сходимости к типам EVD



Теоремы Караматы
Jovan Karamata (1902-1967)
Теоремы Караматы
Быстро изменяющиеся функции

Теоремы Караматы
Регулярно изменяющиеся функции

Видим, что в признаках для II и III типов EVD мы хотим, чтобы функции выживаемости были регулярно изменяющимися.
Теоремы Караматы
Karamata's theorem

Теоремы Караматы
Karamata's representation theorem

Теоремы Караматы
Karamata's characterization theorem

Дополнения к теоремам Караматы
Необходимый и достаточный признаки для EVT type I
требует 2 дополнений к теоремам Караматы: понятий П-вариации и Г-вариации.
Дополнения к теоремам Караматы
Необходимый и достаточный признаки для EVT type I
требует 2 дополнений к теоремам Караматы: понятий П-вариации и Г-вариации.
Дополнения к теоремам Караматы

Дополнения к теоремам Караматы

Дополнения к теоремам Караматы

Необходимый и достаточный признаки сходимости к EVD type II

Здесь мы обобщаем достаточный признак фон Мизеса, используя теоремы Караматы о регулярной вариации. Сравним с признаком фон Мизеса:
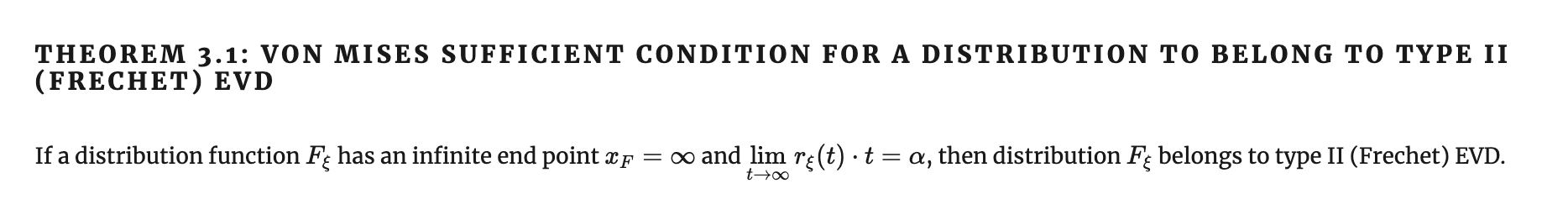
Необходимый и достаточный признаки сходимости к EVD type III

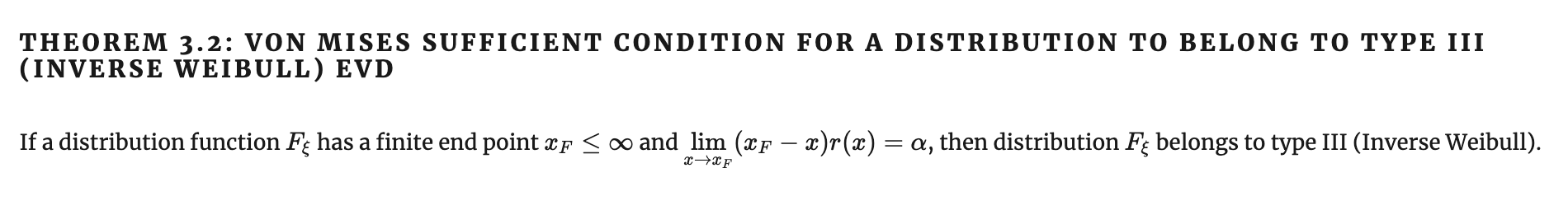
Аналогично. Сравним с признаком фон Мизеса:
Необходимый и достаточный признаки сходимости к EVD type I


Это условие чуть обобщает достаточный признак фон Мизеса, давая больше свободы в выборе вспомогательной функции. Сравним с формулировкой признака фон Мизеса:
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении

Approximately 40% of the Netherlands is below sea level. Much of it has to be protected against the sea by dykes. These dykes have to withstand storm surges that drive the seawater level up along the coast. The Dutch government, balancing considerations of cost and safety, has determined that the dykes should be sufficiently high that the probability of a flood (which occurs when the seawater level exceeds the top of the dyke) in a given year is \( 10^{−4} \) . The question is then: how high should the dykes be built to meet this requirement?
https://ss.amsi.org.au/wp-content/uploads/sites/85/2021/09/quiz-modern_intro_extremes_solutions.pdf
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
https://education.nationalgeographic.org/resource/doggerland/
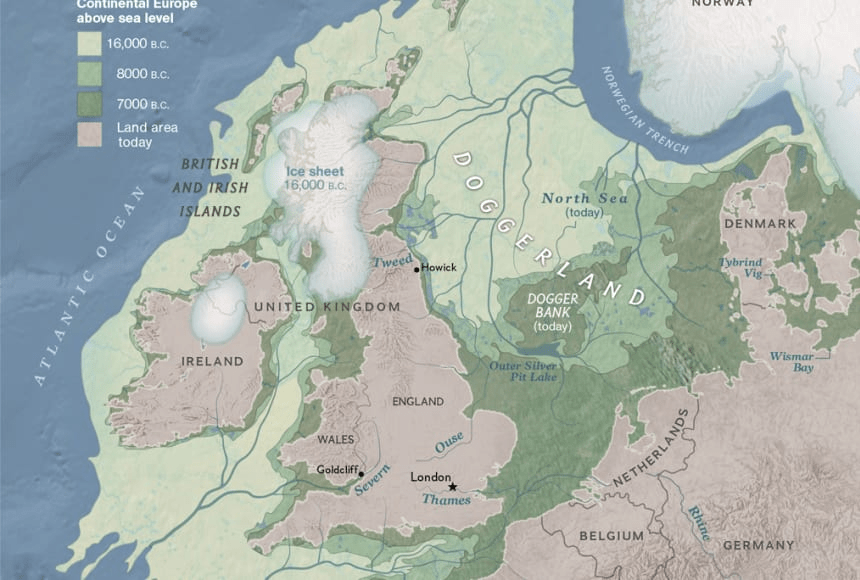
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
Задача, поставленная правительством Нидерландов, не решаема чисто эмпирическим путем, потому что чтобы эмпирически найти квантиль уровня 0.0001, нужно ~10000 точек наблюдений за годовым максимумом уровня моря. Мало того, что их никто не вел так долго, 10000 лет назад не было никакого Северного моря, там был Доггерланд (а 10000 лет вперед, соответственно, не будет никакой Голландии...).
Поэтому эмпирические данные накапливаются гораздо медленнее, чем движется интересующее нас распределение.


James Pickands III
Laurens de Haan
A.A.(Guus) Balkema
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
Обобщенное распределение Парето a.k.a.
Generalized Pareto Distribution (GPD)
Сравните с обобщенным распределением экстремального значения:
Обобщенное распределение Парето a.k.a.
Generalized Pareto Distribution (GPD)

Первый день остатка вашей жизни
Обобщенное распределение Парето a.k.a.
Generalized Pareto Distribution (GPD)

Первый день остатка вашей жизни
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении

Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
Доказательство прямого утверждения

Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении

Доказательство прямого утверждения
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении

Доказательство прямого утверждения
Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
Доказательство прямого утверждения

Теорема Пикандса-Балкемы-де Гаана a.k.a. вторая теорема об экстремальном значении
Доказательство обратного утверждения

Когда EVT не работает:
- Максимумы дискретных случайных величин не сходятся к распределению экстремального значения
- Максимум из Пуассоновских случайных не сходится к распределению экстремального значения
- Максимум из геометрического распределения не сходится к распределению экстремального значения
Когда EVT не работает: достаточное условие

Когда EVT не работает: геометрическое

Когда EVT не работает: Пуассон

Примеры: BLAST и статистика Карлина-Альтшуля
https://www.ebi.ac.uk/jdispatcher/sss/ncbiblast
Примеры: BLAST и статистика Карлина-Альтшуля
https://www.ebi.ac.uk/jdispatcher/sss/ncbiblast
Примеры: BLAST и статистика Карлина-Альтшуля
GGCACGAGCCACCGTCCAGGGAGCAGGTAGCTGC
GGCTGGGAGCGTGCTTTCCACGACGGTGACACGC
TTCCGGGTCACTGCCATGGAGGAGCCGCAGTCA
}
N=100000
Имеется банк данных, содержащий N последовательностей ДНК:
Дана последовательность ДНК-поисковый запрос:
GGTCGATGCCGTAGT
...
https://www.ebi.ac.uk/ena/browser/api/fasta/AF307851.1?lineLimit=1000
Примеры: BLAST и статистика Карлина-Альтшуля
GGTCGATGCCGTAGT
TTCCGGGTCACTGCCATGGAGGAGCCGCAGTCA
++++--++++-+-+-
Score = 5
Сопоставляем исследуемую последовательность с каждой последовательностью ДНК в банке данных, вычисляем расстояние Левенштейна (Score) в стиле команды diff:
Пусть лучший скор оказался равен 5. Это случайность или нет? Если в базе данных из N случайных последовательностей поискать совпадение с нашей, каков шанс, что лучшее совпадение будет иметь Score=5 и выше?
Примеры: BLAST и статистика Карлина-Альтшуля
\( p(Score \ge x=5) = e^{-A e^{-kx}} \)
где A, k - параметры, зависящие от длины входной последовательности, размера банка данных и алфавита
Ответ: вероятность получить лучший \( Score \ge x=5 \) подчиняется распределению Карлина-Альтшуля, которое является просто частным случаем распределения Гумбеля.
Примеры: функция дожития человека

Примеры: функция дожития человека
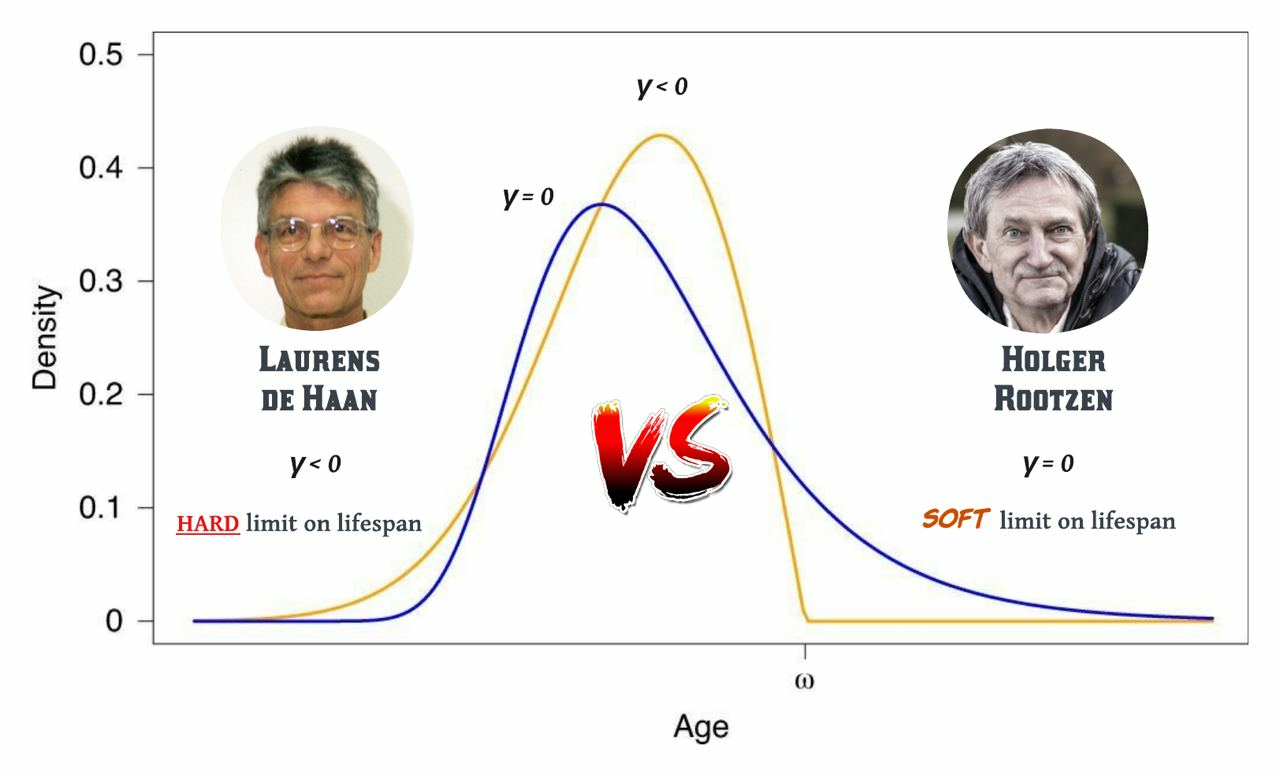
Примеры: функция дожития человека
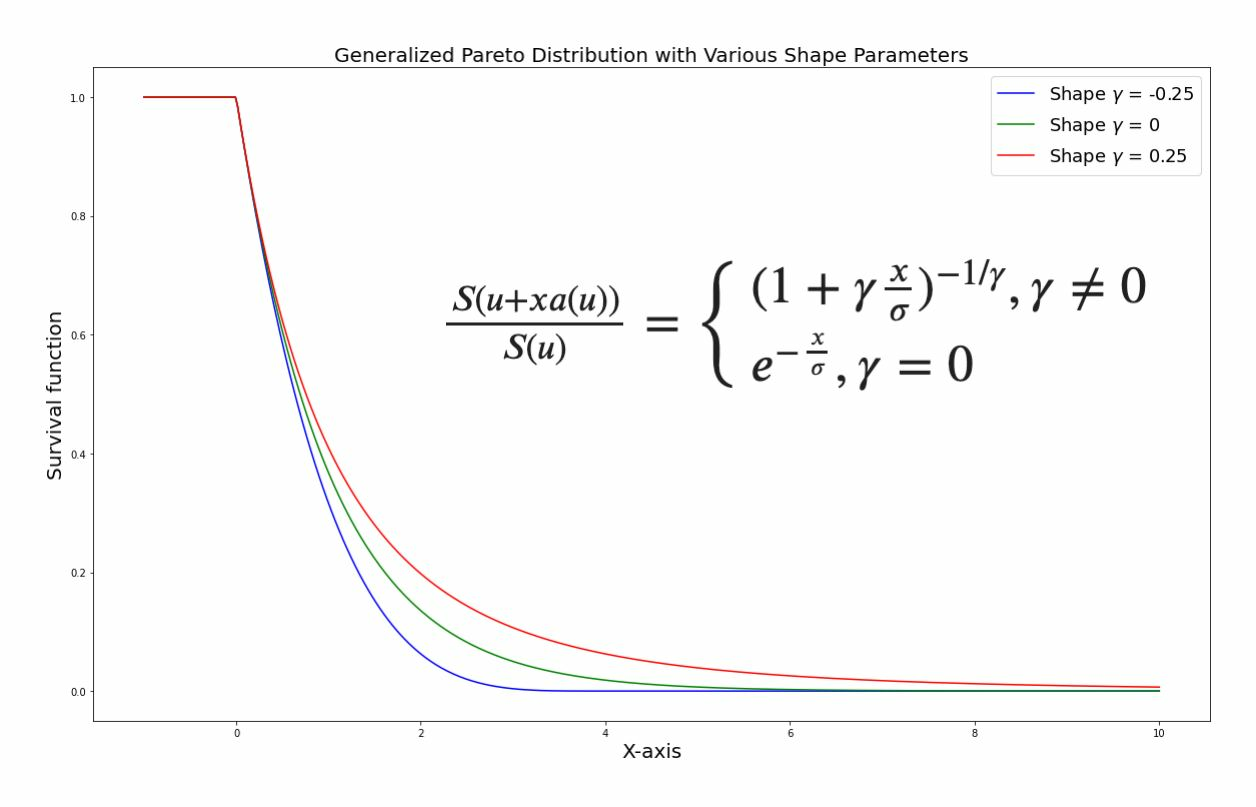
Примеры: функция дожития человека

https://www.supercentenarians.org/en/publications/
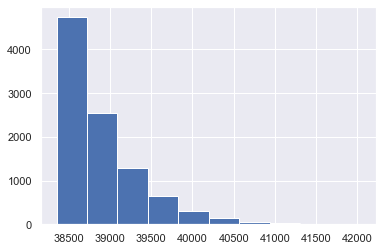
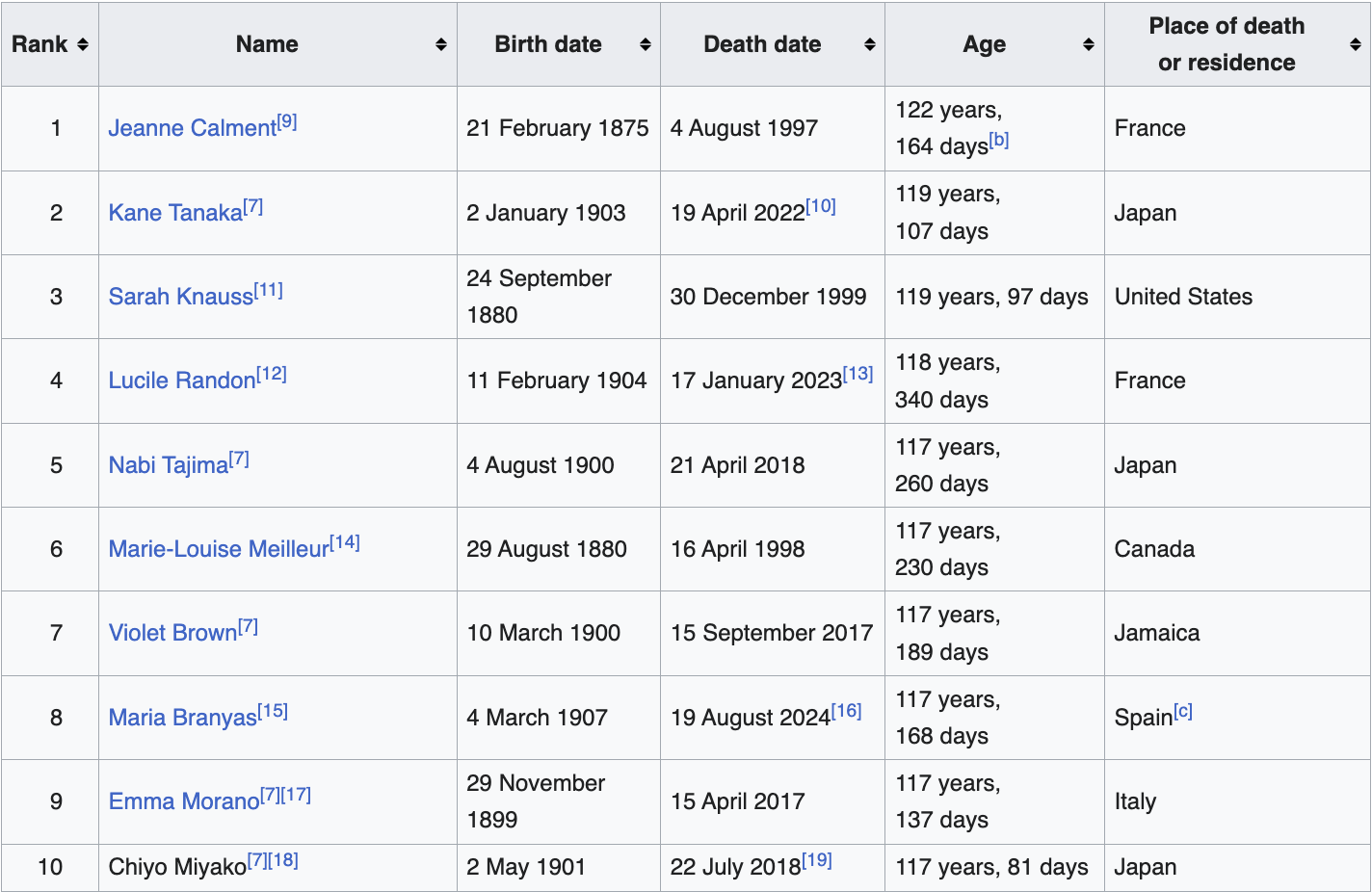
Примеры: функция дожития человека
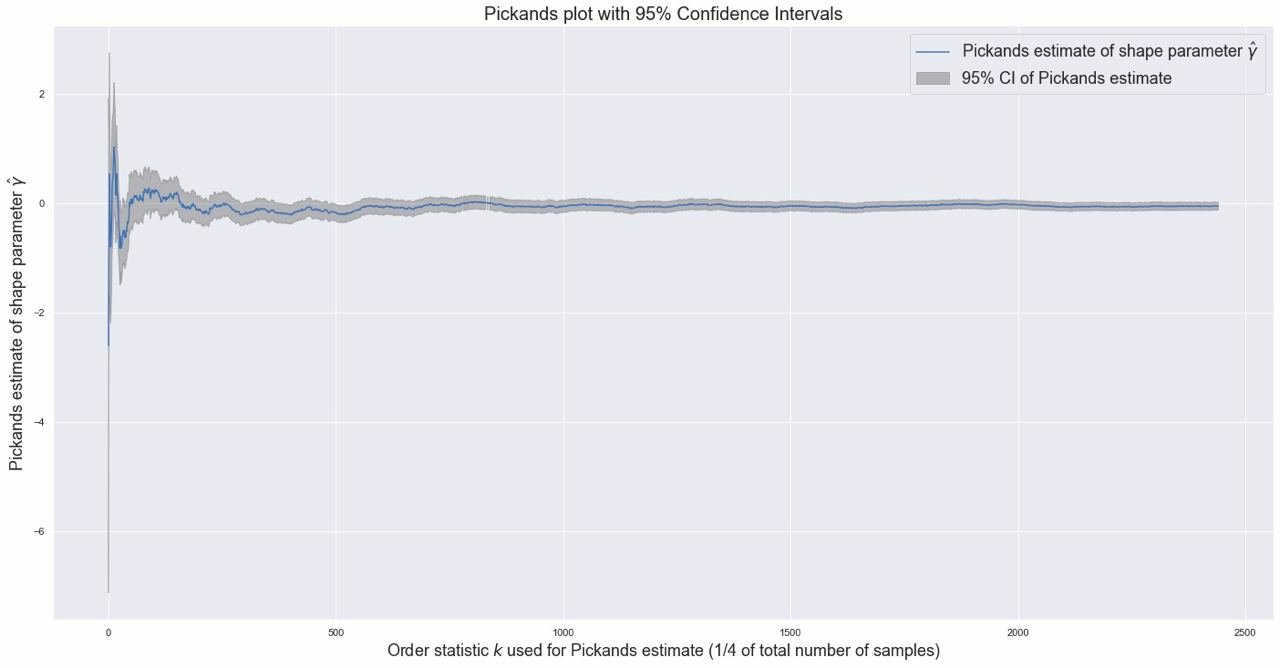
Примеры: функция дожития человека
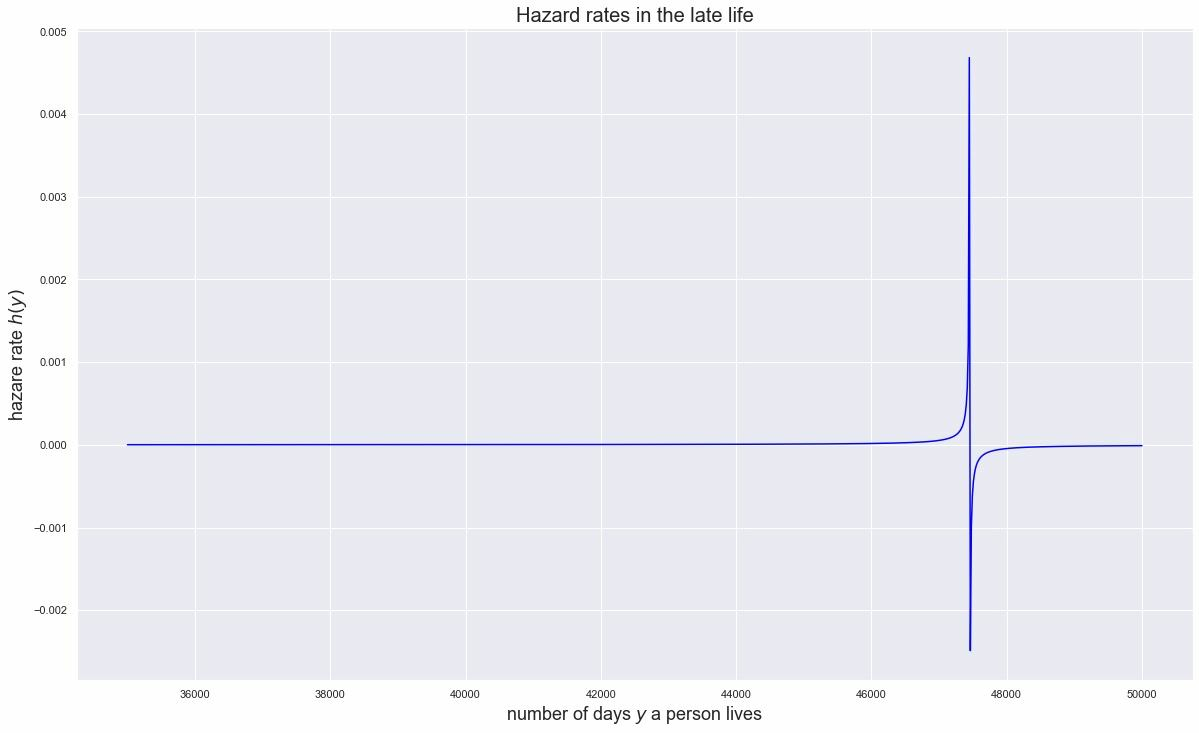
Примеры: функция дожития человека
С практической точки зрения разница между подходами Рутцена и де Гаана действительно невелика, предел все равно очень далеко.
Рутцен далее спекулирует, что популярная модель для кривой дожития, распределение Гомпертца, которая работает в молодости, может применяться и в геронтологии до самых поздних лет жизни. Эта модель подразумевает γ=0, выход риска смерти на плато и отсутствие жесткого предела продолжительности жизни.
На мой взгляд, подход все-таки грубоватый для супердолгожителей. Легкие хвосты распределения Гомпертца невозможны при γ<0, который мы все-таки уверенно наблюдаем. Поэтому для нужд моделирования статистики супердолгожителей на мой взгляд лучше брать альтернативные модели с толстыми хвостами типа slash Gompertz.
Ну и, резюмируя, “я собираюсь жить вечно, пока все идет нормально” не работает. Просто хорошая медицина не поможет вам прожить сильно за сотню, нужна геронтология.
https://github.com/BurkovBA/human-lifespan-limit/blob/main/supercentenarians.ipynb
Примеры: функция дожития человека
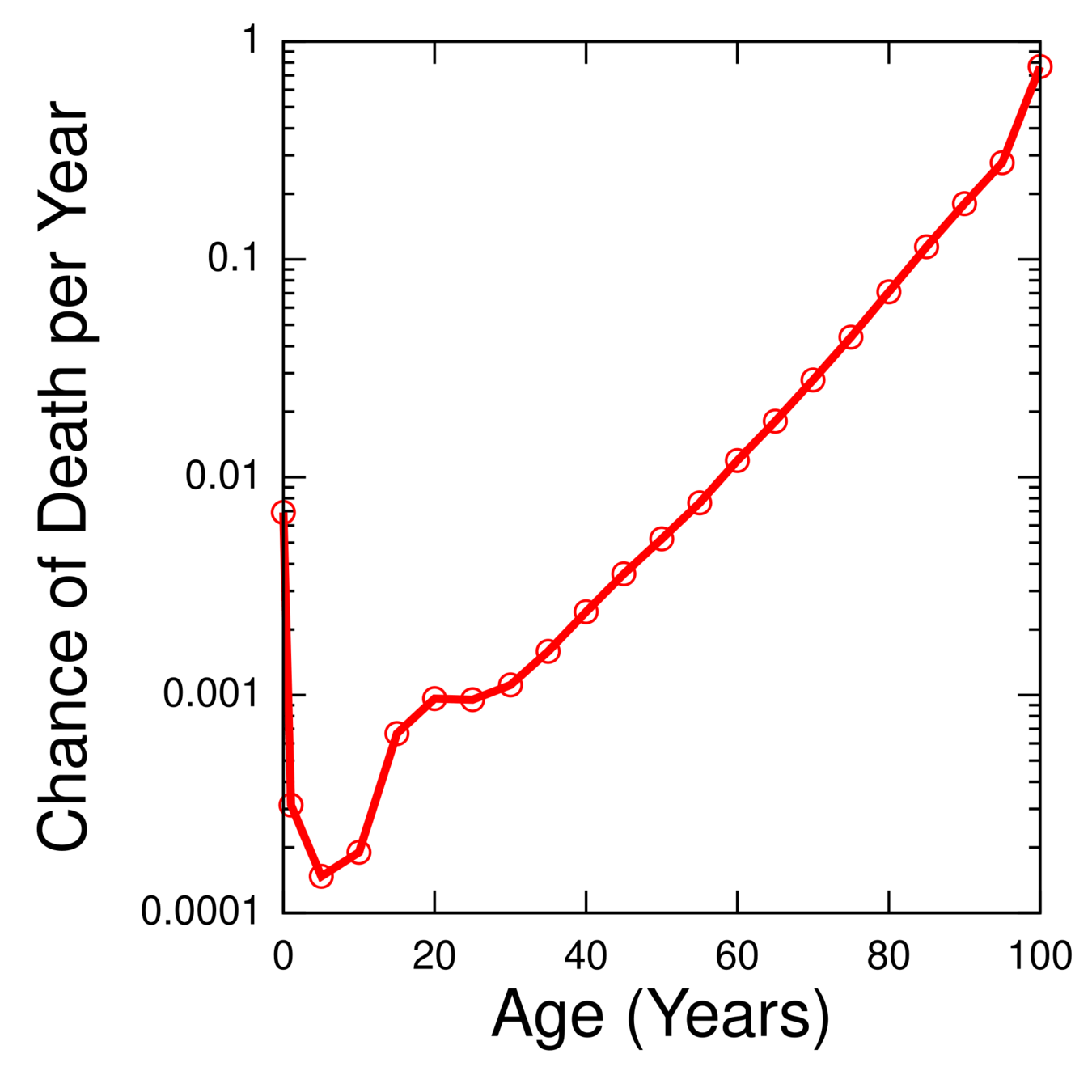
https://en.wikipedia.org/wiki/Gompertz%E2%80%93Makeham_law_of_mortality
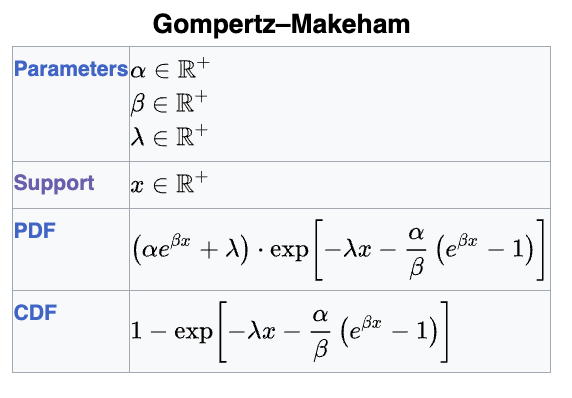
Примеры: функция дожития человека
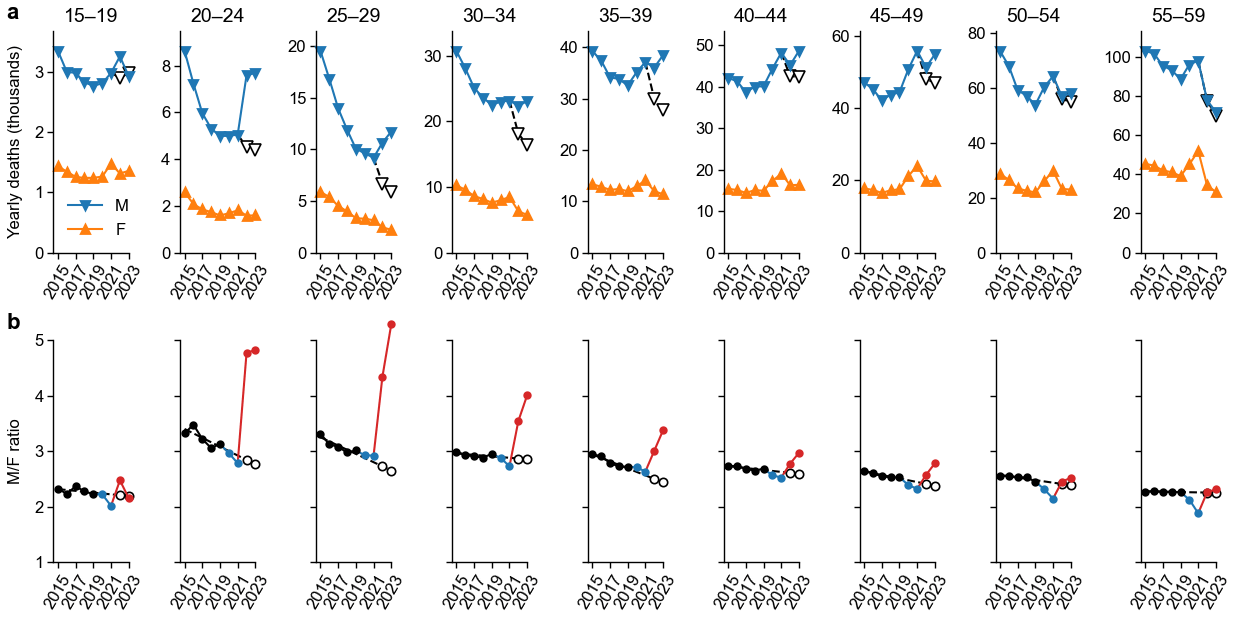
https://github.com/dkobak/excess-mortality-war

Дмитрий Кобак
Примеры: функция дожития человека
https://en.wikipedia.org/wiki/Aubrey_de_Grey

Гипотеза Обри де Грея:
Первый человек, который доживет до 200 лет, будет старше первого человека, который доживет до 1000 лет, на 5 лет.
Think about it с точки зрения EVT.
Примеры: функция дожития голого землекопа

https://pmc.ncbi.nlm.nih.gov/articles/PMC6615856/
Примеры: функция дожития голого землекопа
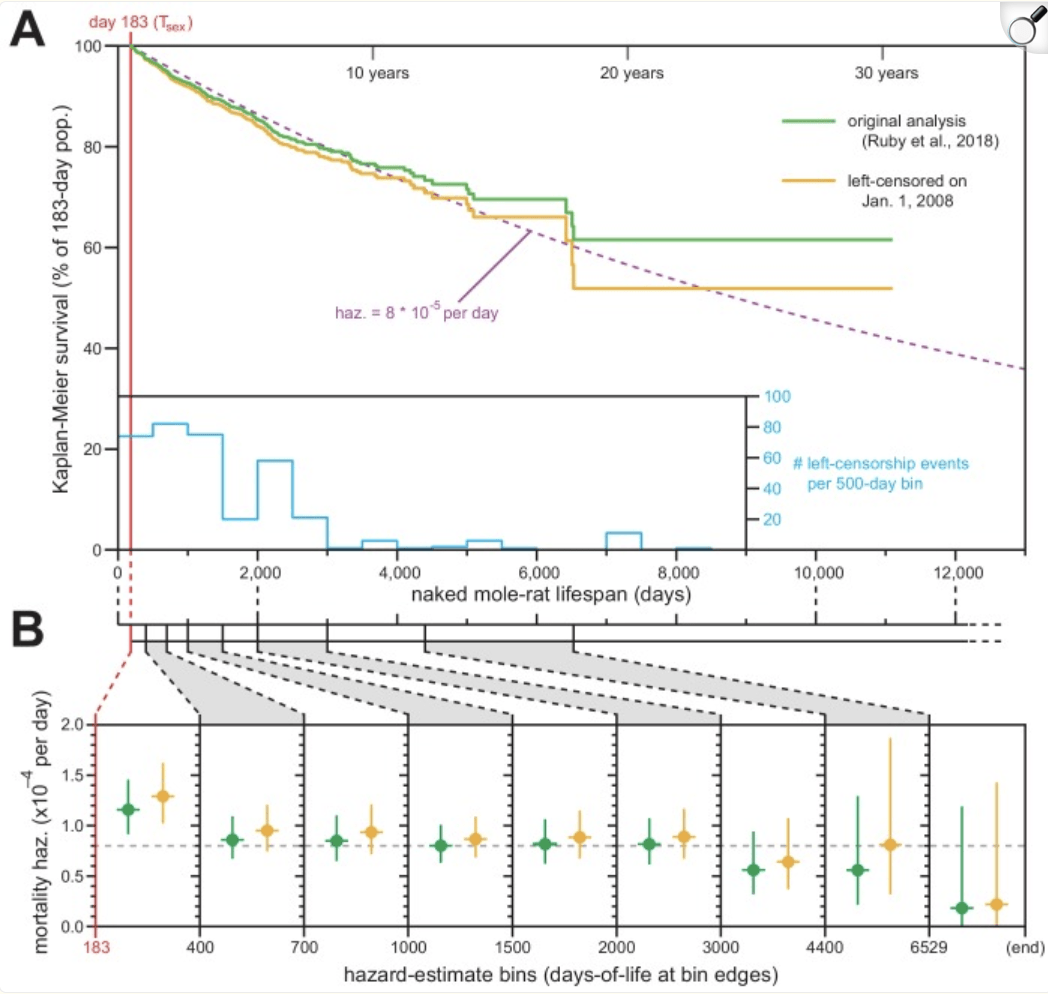
https://pmc.ncbi.nlm.nih.gov/articles/PMC6615856/
"For most adult mammals, the risk of death increases exponentially with age, an observation originally described for humans by Benjamin Gompertz. We recently performed a Kaplan–Meier survival analysis of naked mole-rats (Heterocephalus glaber) and concluded that their risk of death remains constant as they grow older (Ruby et al., 2018). Dammann et al. suggest incomplete historical records potentially confounded our demographic analysis (Dammann et al., 2019). In response, we applied the left-censorship technique of Kaplan and Meier to exclude all data from the historical era in which they speculate the records to be confounded. Our new analysis produced indistinguishable results from what we had previously published, and thus strongly reinforced our original conclusions."
Примеры: Value-at-Risk и Expected Shortfall
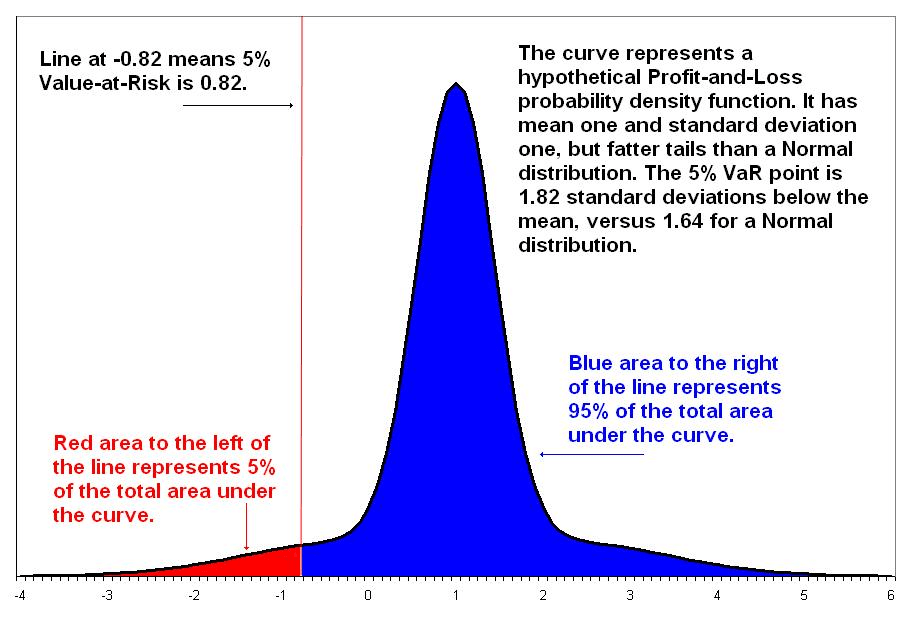
\( VaR_{\alpha}(X) = \{ \inf x; S(x) \ge 1- \frac{1}{\alpha} \} \)
\( ES_\alpha(X) = -\frac{1}{\alpha} \int_0^\alpha VaR_\gamma(X) \, d\gamma \)
Примеры: Value at Risk и Expected Shortfall
Вторая теорема в действии: принимаем \( u \) за VaR уровня 5%, аппроксимируем хвост распределения обобщенным распределением Парето, подгоняем параметры shape/scale/loc наибольшим правдоподобием или чем-то таким и считаем VaR/ES.
\( \frac{S(u + x g(u))}{ S(u) } = (1 + \gamma \frac{x - \mu}{\sigma})^{-1/\gamma} \)
Примеры: максимумы уровня воды
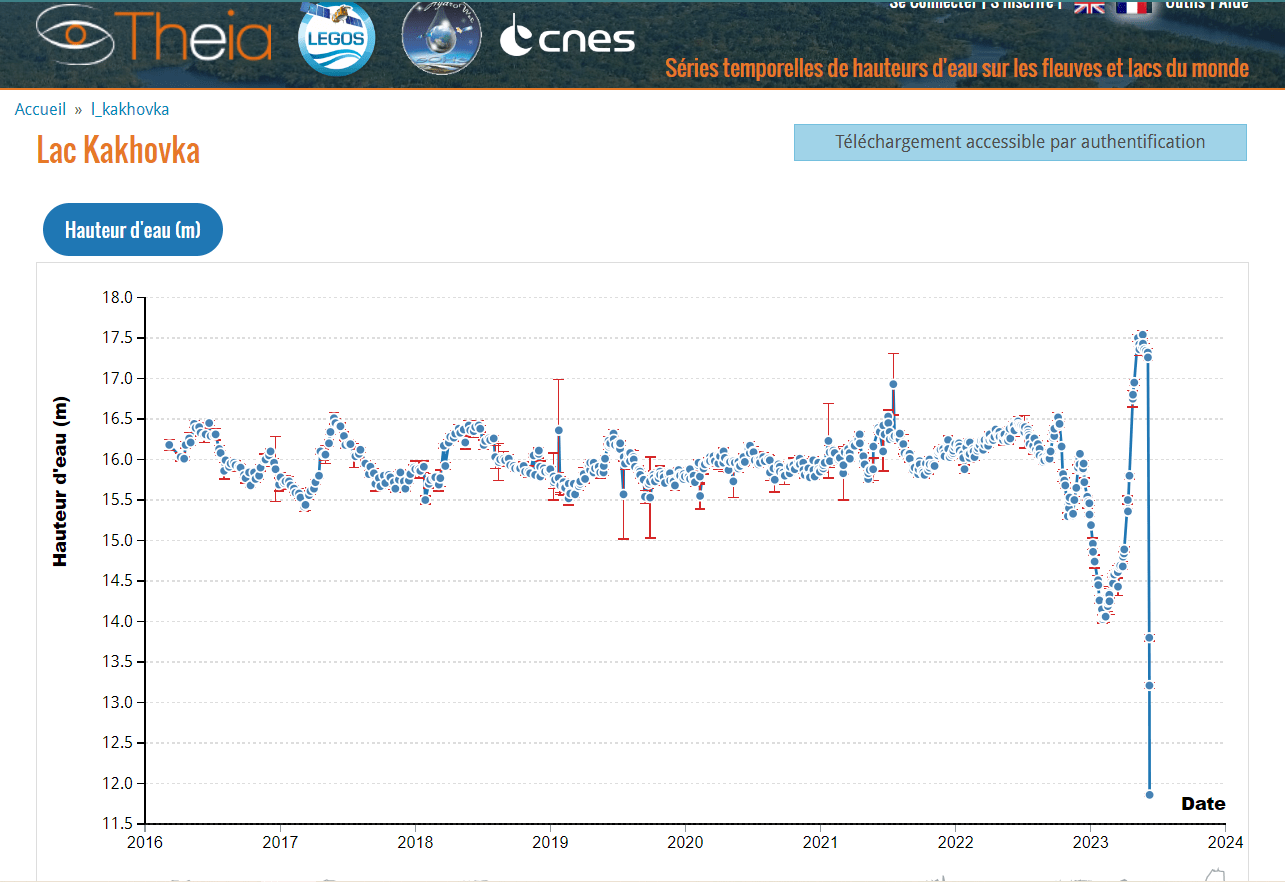
https://www.theia-land.fr/en/kakhovka-hydroweb-data-shows-a-reservoir-turned-river/

Примеры: максимумы уровня воды
https://ss.amsi.org.au/wp-content/uploads/sites/85/2021/09/quiz-modern_intro_extremes_solutions.pdf
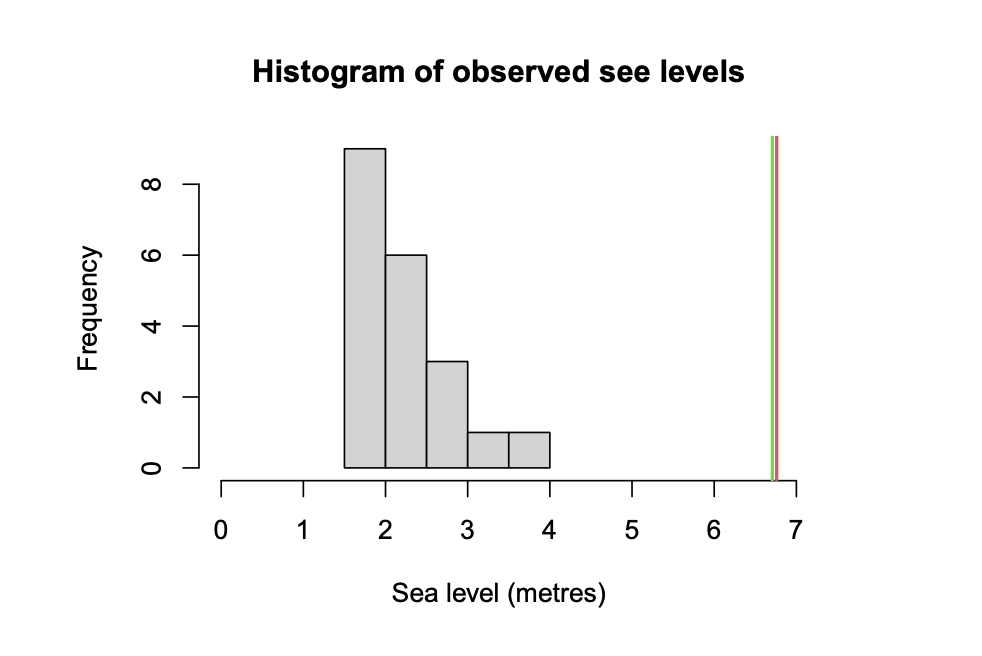
\( \frac{S(u + x g(u))}{ S(u) } = (1 + \gamma \frac{x - \mu}{\sigma})^{-1/\gamma} \)
Опять же, фиттим параметры
по наблюдаемому хвосту:
и считаем квантиль GPD уровня 0.0001. В случае голландских dykes выходит 6.7 метра. Случай Каховки оставляю читателю.
Обобщения
- Работает для минимумов примерно так же, как и для максимумов.
- Работает для k-ой порядковой статистики, давая Пуассоно-подобное распределение
- Можно обобщать на не совсем независимые случайные величины
- Можно обобщать на многомерные случайные величины и случайные (стохастические) процессы
K-ые порядковые статистики

K-ые порядковые статистики

Случай не-независимых случайных величин
TODO
Многомерные случайные величины и стохастические процессы
TODO
Спасибо за внимание!
Полные доказательства всех утверждений: https://borisburkov.net/2023-04-30-1/
✉ BurkovBA@gmail.com
@BurkovBA
