deck

Байесовские и вариационные методы в нейронных сетях

часть 2

План

постановка задачи оценки неопределенности модели на примере байесовской линейной регрессии
вариационный вывод и стохастический вариационный вывод, проблемы стохастического вывода
вариационный автокодировщик: ELBO, SVI, дважды стохастический вариационный вывод, reparametrization trick
дропауты
вариационный дропаут

Пример решаемой проблемы

Предположим, условная компания ДомКлик открывает новый филиал в городе Кобылозаводске, и предлагает сервис оценки справедливой рыночной цены квартиры в этом городе.

У дата-сайнтистов ДомКлика имеется обучающая выборка из n квартир в Кобылозаводске, про каждую квартиру номер i известна стоимость ее продажи/покупки y_i и вектор характеристик данной квартиры x_i, которые будут использоваться как факторы линейной регрессии.

Пример решаемой проблемы

Фреквентист просто построит линейную регрессию, которая лучше всего описывает данные.

Фреквентист выберет те веса w, которые максимизируют вероятность наблюдать цены y при заданных факторах X.

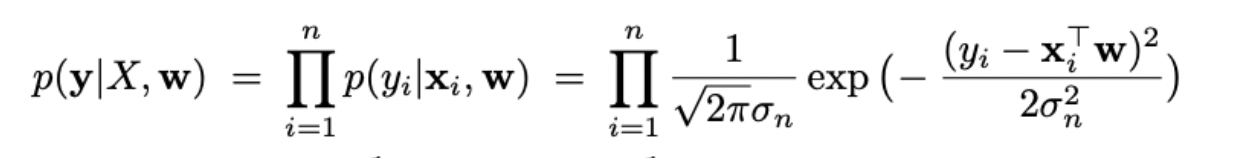
Пример решаемой проблемы

Байесианец скажет, что на основании опыта других городов он имеет априорное представление о том, какими могут быть правдоподобные коэффициенты регрессии w.

Если ему нужно будет выбрать из всех регрессий одну, то он выберет ее на основе максимизации апостериорной вероятность наблюдать ее веса факторов, с учетом наблюдаемых данных.

Лучше, однако, рассчитать вероятности каждой регрессии в ансамбле.

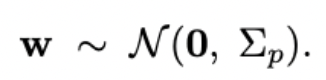
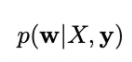
Пример решаемой проблемы

Байесианец также может вычислить целое распределение возможных цен на данную квартиру исходя из моделей, имеющихся в его ансамбле. Этим распределением можно будет пользоваться как оценкой неопределенности прогноза модели.

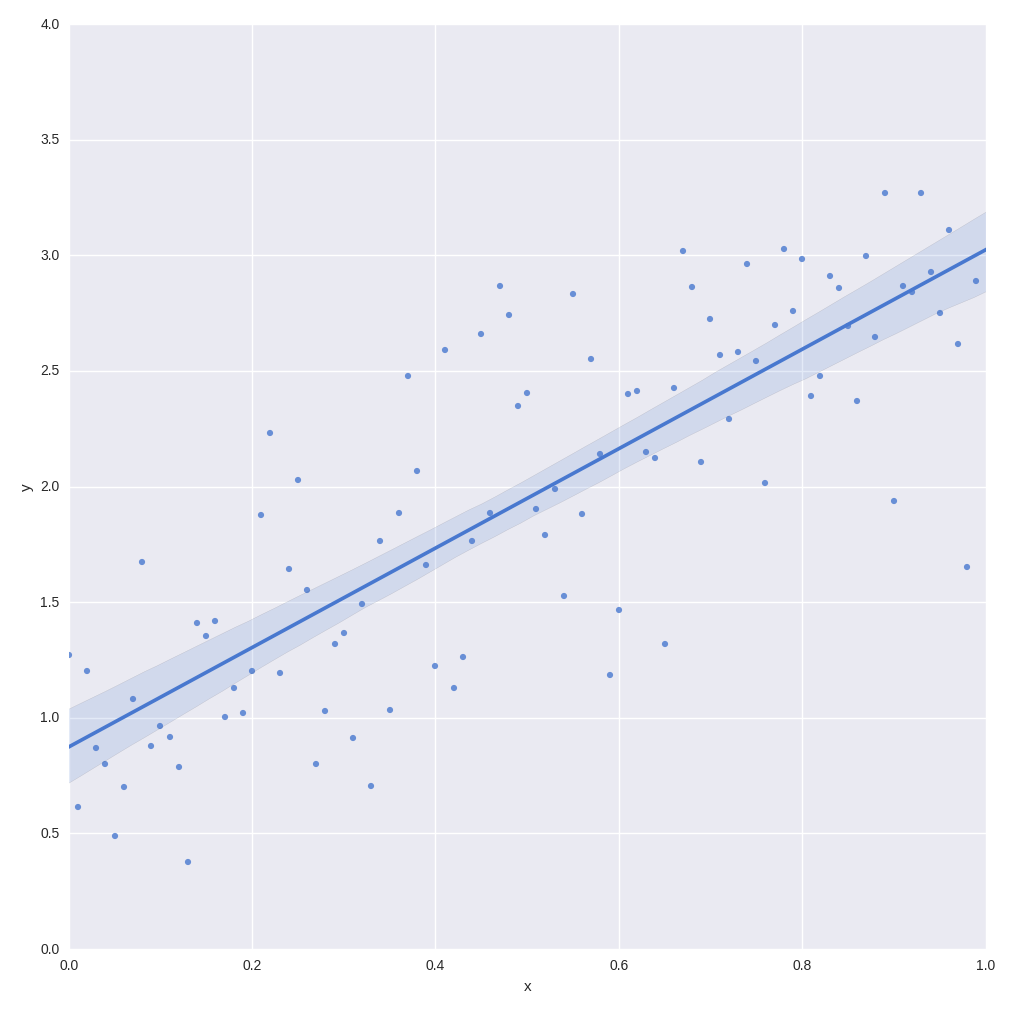
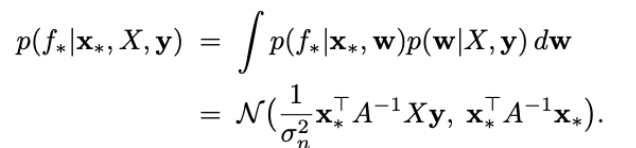
Затем можно вычислить взвешенное среднее цен на данную квартиру по ансамблю регрессий.

Можно ли так же для нейронных сетей?

Как получить оценки неопределенности предсказания нейронных сетей в задачах регрессии и классификации?

Вариационный вывод

p(x, \theta) = p(x | \theta) \cdot p(\theta) = p(\theta | x) \cdot p(x)

likelihood

prior

posterior

evidence

Задача: вычислить posterior.

Препятствие: проблема обычно состоит в том, что evidence is intractable.

p(x) = \int p(x | \theta) p(\theta) d{\theta}

- не вычисляемо

Вариационный вывод

p(\theta | x) \approx q(\theta) \in \mathcal{Q}

KL(q(\theta) \Vert p(\theta | x)) \to \min\limits_{q(\theta) \in \mathcal{Q}}

KL(q(\theta) \Vert p(\theta | x)) = \int q(\theta) \log \frac{q(\theta)}{p(\theta | x)} d\theta \ge 0

Из лекции Д.Ветрова на DeepBayes2019

Вариационный вывод

Из лекции David Blei на MLSS 2019

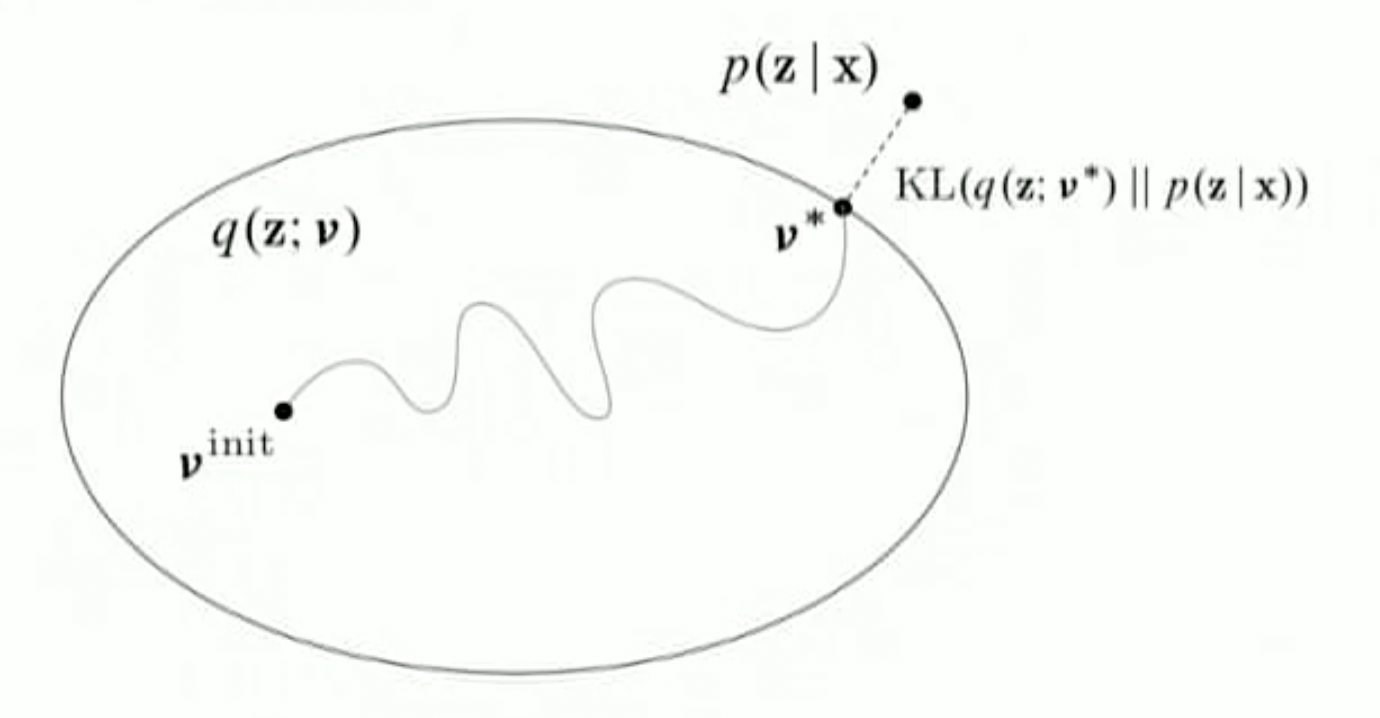
Например: p(z|x) = sin(z), а Q - класс всех многочленов не

выше 3 степени. Тогда мы ищем guide среди функций вида:

q_{v}(z) = v_1 z^3 + v_2z^2+v_3z+v_4

Вариационный вывод

\log p(x) = \int q(\theta) \log{p(x)} d\theta = \int q(\theta) \log \frac{p(x, \theta)}{p(\theta | x)} d\theta

= \int q(\theta) \log \frac{p(x, \theta) q(\theta)}{p(\theta | x) q(\theta)} d\theta

= \int q(\theta) \log \frac{p(x, \theta)}{q(\theta)} d\theta + \int q(\theta) \log \frac{q(\theta)}{p(\theta | x)} d\theta

= \mathcal{L}(q(\theta)) + KL(q(\theta) \Vert p(\theta | x))

Из лекции Д.Ветрова на DeepBayes2019

ELBO

\log p(x) = \mathcal{L}(q(\theta)) + KL(q(\theta) \Vert p(\theta | x))

ELBO - Evidence lower bound

KL \ge 0 \Rightarrow \log p(x) \ge \mathcal{L}(q(\theta))

KL(q(\theta) \Vert p(\theta | x)) \to \min \Leftrightarrow \mathcal{L}(q(\theta)) \to \max

Из лекции Д.Ветрова на DeepBayes2019

ELBO

\mathcal{L}(q(\theta)) = \int q(\theta) \log \frac{p(x, \theta)}{q(\theta)} d\theta = \int q(\theta) \log \frac{ p(x|\theta) p(\theta) }{q(\theta)} d\theta

Из лекции Д.Ветрова на DeepBayes2019

= \int q(\theta) \log p(x| \theta) d\theta + \int q(\theta) \log \frac{ p(\theta) }{q(\theta)} d\theta

= \mathbb{E}_{ q(\theta) } \log p(x|\theta) - KL(q(\theta) \Vert p(\theta))

Expected log-likelihood

Regulariser term

KL-divergence

Стохастический вариационный вывод (SVI)

D. Wingate, T. Weber: https://arxiv.org/pdf/1301.1299.pdf

Стохастический вариационный вывод (SVI)

Основная практическая проблема стохастического вариационного вывода: как добиться того, чтобы дисперсия оценки градиента была не слишком велика?

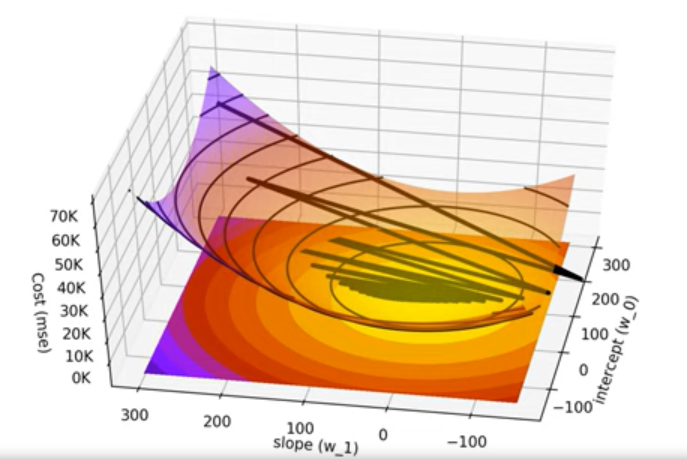
Стохастический вариационный вывод (SVI)

Идеальный случай: дисперсия градиента убывает с ростом размера мини-батча. Тогда достаточно взять видеокарту с большим количеством видеопамяти, чтобы получить более точную оценку градиента на каждой итерации и лучшую сходимость.

Стохастический вариационный вывод (SVI)

Оригинальная статья David Wingate, Theo Weber по Stochastic Variational Inference: https://arxiv.org/pdf/1301.1299.pdf
Статья Kingma, Welling по VAE как машинки для SVI: https://arxiv.org/pdf/1312.6114.pdf
Статья Kingma, Welling по Variational Dropout как реализации SVI: https://arxiv.org/pdf/1506.02557.pdf
Тьюториал David Blei по VI и SVI: https://arxiv.org/pdf/1601.00670.pdf
Лекция Дмитрия Ветрова по VI и ELBO: https://www.youtube.com/watch?v=xH1mBw3tb_c
Лекция Дмитрия Ветрова по SVI и VAE: https://www.youtube.com/watch?v=tjT4Wf86FMM

Ссылки:

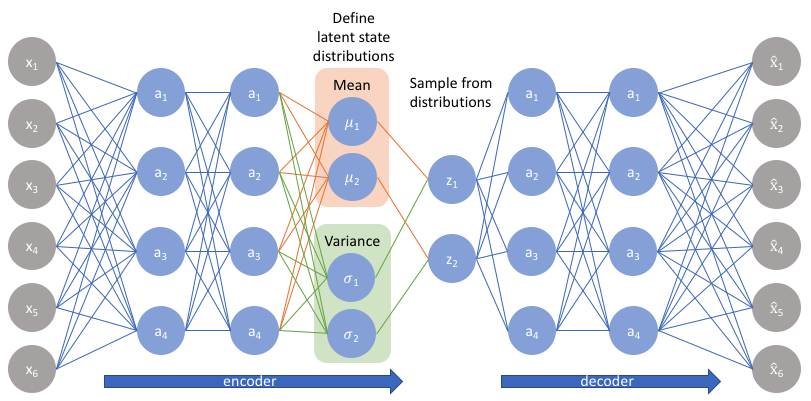
Вариационный автокодировщик (VAE)

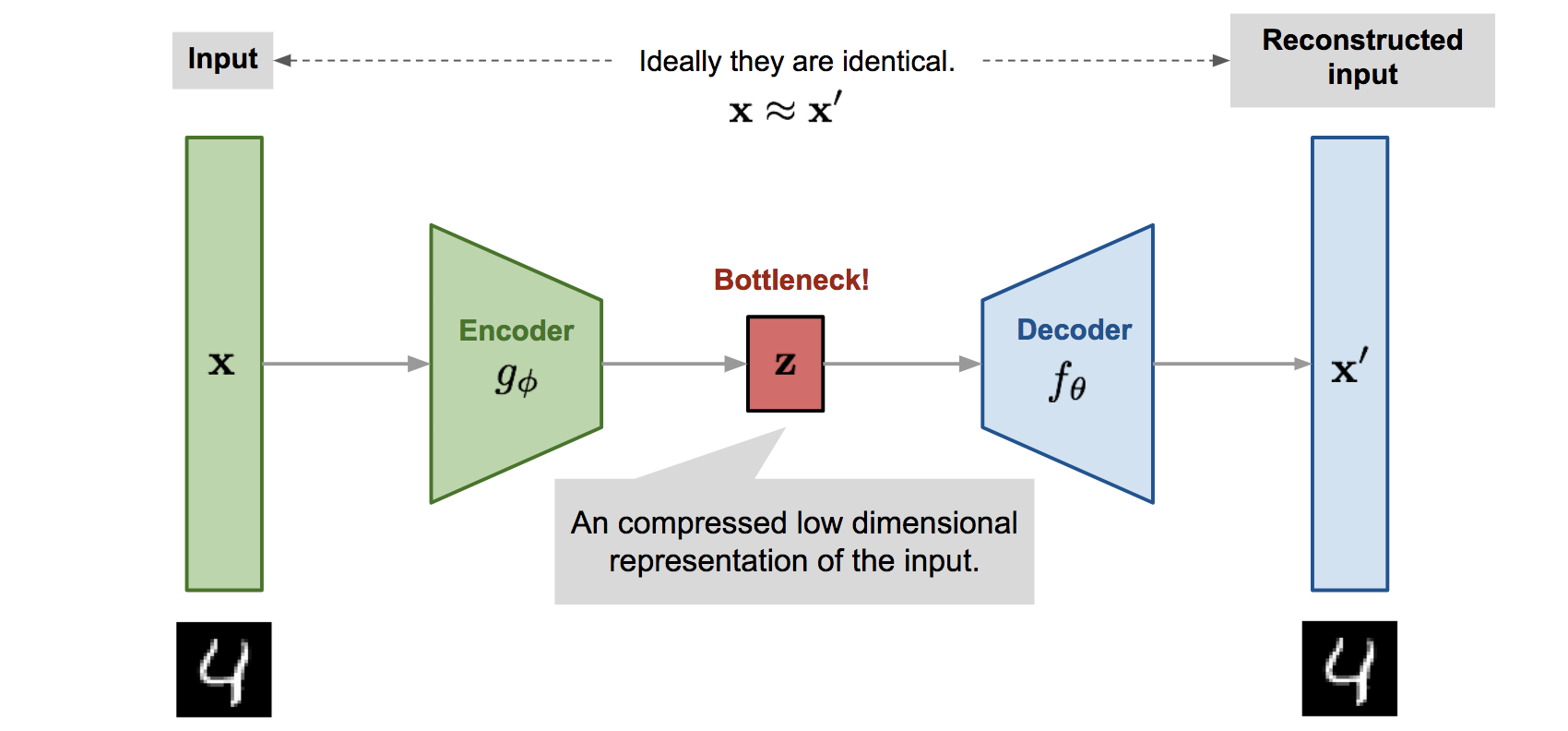
Задача любого автокодировщика - поставить в соответствие входным данным x эмбеддинг z в пространстве низкой размерности

Зачем все так сложно?

Дважды стохастический вариационный вывод - неоправданно навороченный алгоритм. Зачем было все так усложнять?

Автокодировщики переобучаются. Особенно, в латентных пространствах z большой размерности (из доклада D.Kingma на ICLR 2014).
Нет непрерывности отображения входов x на латентное пространство.
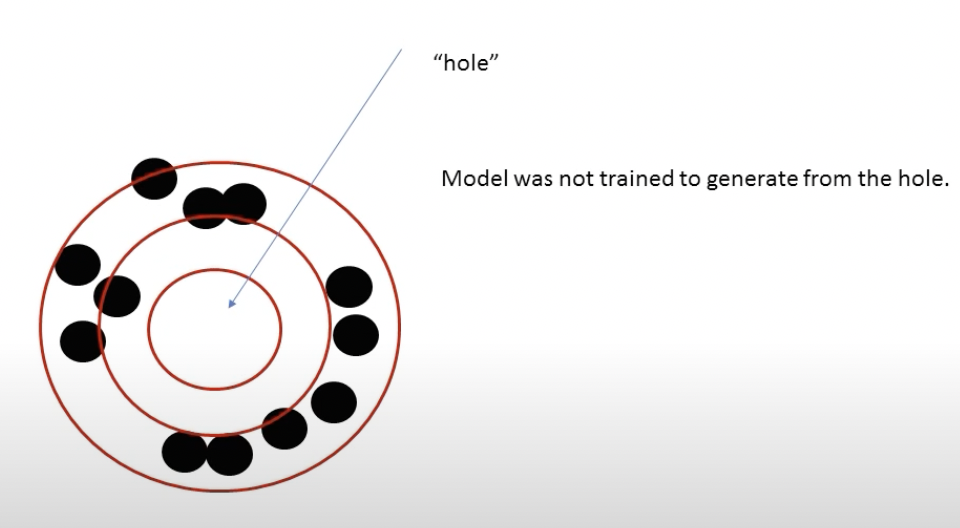
Возможны "дырки" в латентном пространстве, сэмплирование из которых не даст адекватного выхода (из доклада M.Welling на DeepBayes2018)

VAE as EM

Задача похожа на алгоритм EM: поочередно меняем то ϕ, то θ, так, чтобы максимизировать то p(z|x,ϕ) , то p(x'|z,θ).

EM: аналогия с Баумом-Велчем или K-means

Имеется серия бросков монеты: x = [0, 1, 0, 0, 0, 0, 1, 0, 1, 1].

Известно, что есть 2 монеты: честная и жульническая, при каждом броске монета в одном из этих двух состояний, эти вектор этих состояний является скрытыми переменными z.

Есть вектор вероятностей замены монеты с честной на жульническую и обратно и есть вероятность выкинуть орла и решку для честной монеты и для жульнической. Это - параметры модели θ.

Алгоритм ищет такие параметры модели θ, при которых достигается максимум вероятности наблюдать x. Каждая итерация i состоит из 2 шагов, E-step и M-step, когда обновляется то состояние скрытой переменной, то параметров модели:

z(i+1) = \underset{z}{\mathrm{\argmax}}\ p(x|\theta(i), z(i))

\theta(i+1) = \underset{\theta}{\mathrm{\argmax}}\ p(x|\theta(i), z(i))

E-step:

M-step:

VAE as EM

Из доклада M.Welling на DeepBayes2018

Почему бы просто не вычислить q(z) безо всяких reparametrization tricks?

Из доклада M.Welling на DeepBayes2018

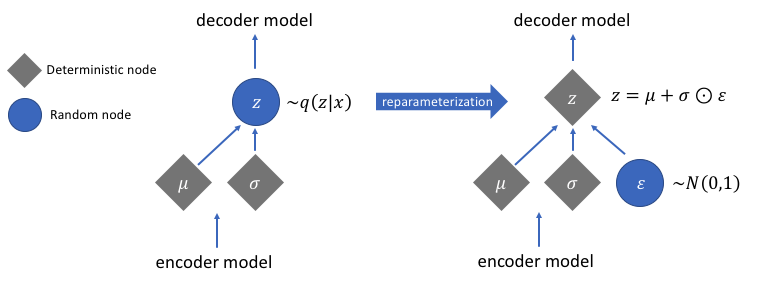
Reparametrization trick

Трюк: превращаем randomness во вход нейронки, а по параметрам нормального распределения тогда можно дифференцировать.

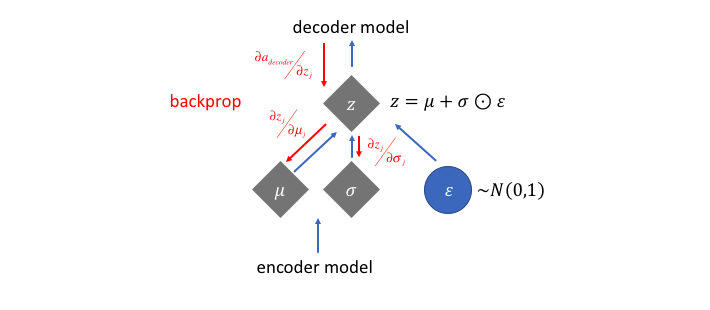
Из: jeremyjordan.me/variational-autoencoders

Дважды стохастический вариационный вывод

Стохастический градиент по параметрам распределения, вычисляемый с помощью reparametrization trick, имеет очень низкую дисперсию, поэтому можно даже не делать minibatch, а брать всего один сэмпл для оценки.

Pyro

Дропаут как регуляризация нейронных сетей

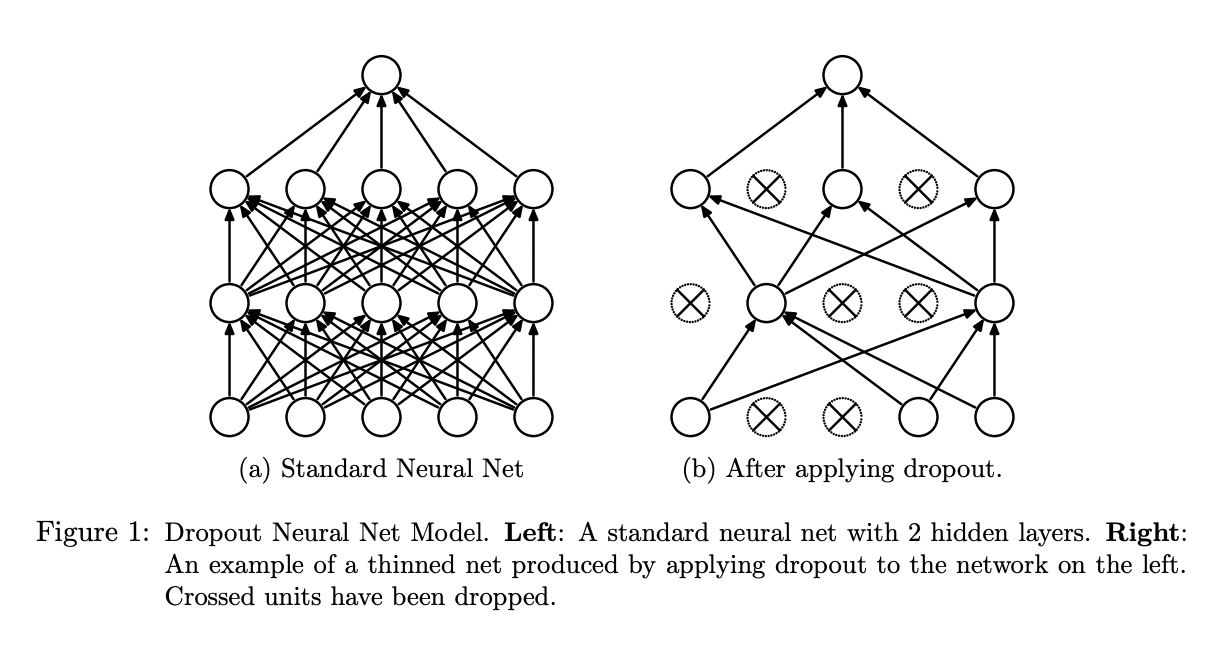
Бинарный или бернуллиевский дропаут

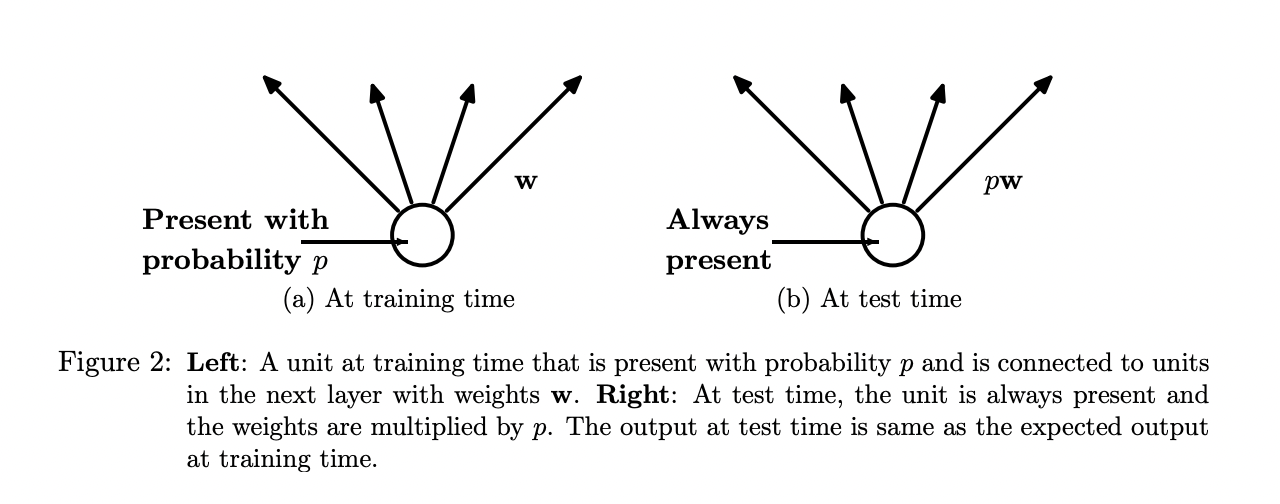
Аналогия с половым размножением - каждая модель

в ансамбле передает половину своих весов потомству с вероятностью p (исходно - 0.5).

Гауссовский дропаут

Srivastava, Hinton et al. позже показали, что Гауссовский Дропаут с непрерывным шумом работает не хуже и быстрее.

\xi_\mu \sim \mathcal{N}(1, \alpha=\frac{p}{(1-p)})

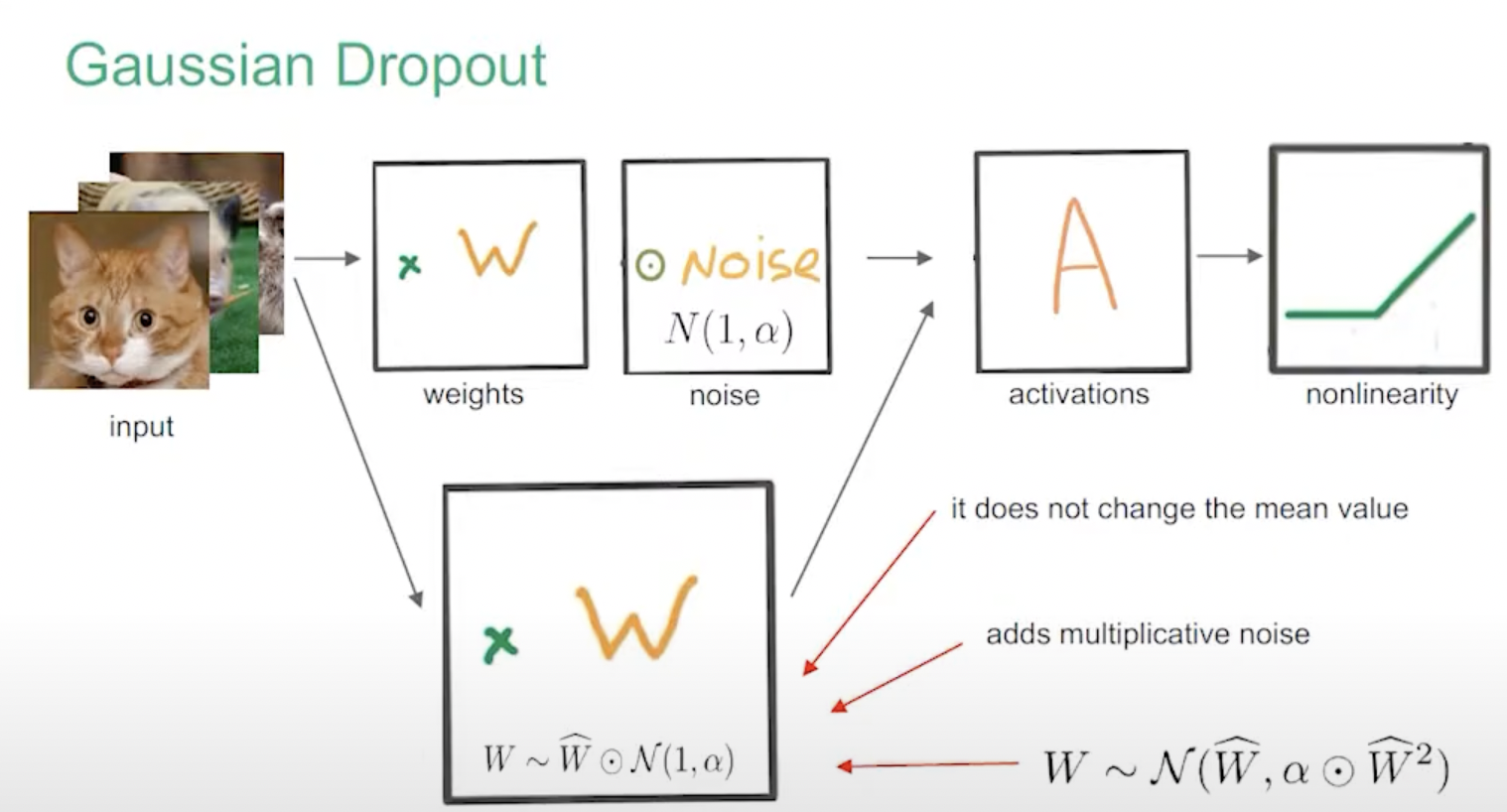
Из доклада Кирилла Неклюдова на DeepBayes2018

Байесовская нейросеть

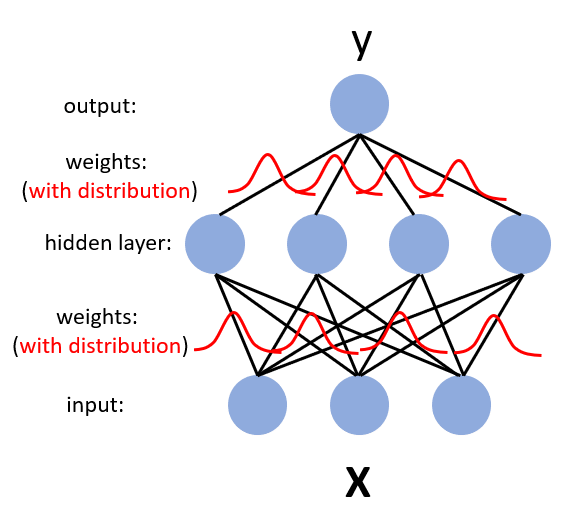
Вариационный дропаут

Гауссовский дропаут эквивалентен добавлению гауссовских prior'ов на ребра. Дальше используем reparametrization trick, подобный VAE, рассматриваем dropout rate как переменную, по которой можно дифференцировать, а случайный шум забираем с псевдовходов сети.

Вариационный дропаут

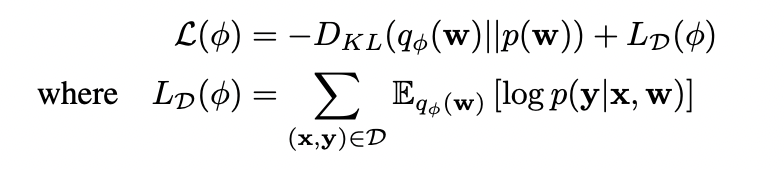
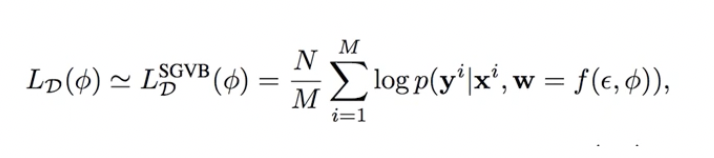
Снова минимизируем ELBO, снова KL-divergence между guide и prior считается аналитически, а матожидание логарифма постериора нужно вычислять стохастическим Монте-Карловским выводом:

Техническая проблема: дисперсия стохастического градиента

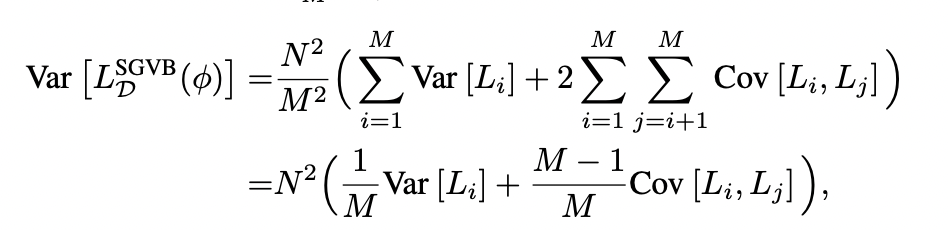
Если ковариация между ячейками ненулевая, то дисперсия градиента не убывает с ростом размера минибатча. Чтобы побороть проблему, делается специальный local reparametrization trick.

L_i =

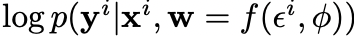
Какая от этого польза?

автоматический отбор фич и (потенциально) архитектур
автоматическая оценка неопределенности предсказания сети

Связь с Relevance Vector Machines (RVM)

Relevance Vector Machines ведут себя примерно как байесовская линейная регрессия с гауссовским prior'ом. То есть они тоже сходятся к kernel ridge regression.

Однако разница в том, что для каждого веса свой коэффициент регуляризации, из-за чего вклад части факторов в итоге обращается в ноль.

Коэффициент регуляризации alpha в Variational Dropout ведет себя аналогично, позволяя делать Automatic Relevance Determination (ARD) части входов или нейронов.

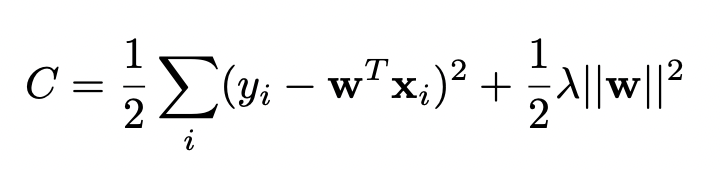
Эквивалентность байесовской нейросети гауссовым процессам

Превосходное изложение доказательства имеется в аппендиксе статьи:

https://arxiv.org/pdf/1506.02157.pdf