206 neutrinos
Vincent DUSAUTOIR
Antoine FORET
Sommaire
- Le projet
- Les calculs
- Exploitations des résultats
Le projet

Jorgen Olaf

Neutrinos
Back to the future
Moyenne arithmétique
M = \frac{x_1 + x_2 + x_3 + ... + x_n}{n}
M=nx1+x2+x3+...+xn
V = M * n
V=M∗n
M = \frac {V + v}{n + 1}
M=n+1V+v
Écart type
\alpha = \sqrt{Var}
α=√Var
Var = \frac {x_1^2 + x_2^2 + x_3^2 + ... + x_n^2} {n} * H^2
Var=nx12+x22+x32+...+xn2∗H2
V = (Var + H^2) * n
V=(Var+H2)∗n
Var = \frac {V + v^2} {n + 1} * H^2
Var=n+1V+v2∗H2
Moyenne quadratique
\overline {x} = \sqrt {\frac{x_1^2 + x_2^2 + x_3^2 + ... + x_x^2}{x_1^2 n + x_2^2n , + x_3^2 n + ... + x_x^2 n}}
x=√x12n+x22n,+x32n+...+xx2nx12+x22+x32+...+xx2
V = x_1^2 + x_2^2 + x_3^2 + ... + x_x^2
V=x12+x22+x32+...+xx2
\overline {x} = \sqrt {\frac {1}{n + 1} * (V + v^2)}
x=√n+11∗(V+v2)
Moyenne Harmonique
H = \frac {1}{\frac {1}{x_1} + \frac {1}{x_2} + \frac {1}{x_3} + ... + \frac {1}{x_n}}
H=x11+x21+x31+...+xn11
V = n / H
V=n/H
H = \frac {n + 1} {V + \frac {1}{v}}
H=V+v1n+1
Exploitations des calculs
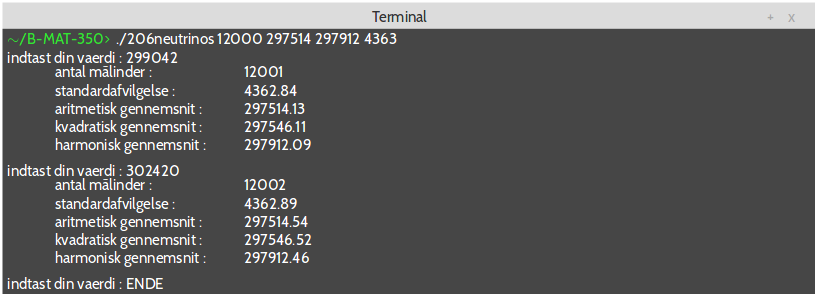
Bonus