Lower Bounds for Private Estimation of  

Victor Sanches Portella

July 2, 2025

joint work with Nick Harvey (UBC)

under All Reasonable Parameter Regimes

Gaussian Covariance Matrices

ime.usp.br/~victorsp

Private Covariance Estimation

\displaystyle x_1, x_2, \dotsc, x_n \sim \mathcal{N}(0, \Sigma)
\displaystyle \Sigma \succ 0

Unknown Covariance Matrix

\displaystyle X \in \mathbb{R}^{d \times n}

\((\varepsilon, \delta)\)-differentially private \(\mathcal{M}\) to estimate \(\Sigma\)

on \(\mathbb{R}^d\)

Goal:

Required even without privacy

Required even for \(d = 1\)

[Karwa & Vadhan '18]

Is this tight?

\((\varepsilon, \delta)\)-DP  \(\mathcal{M}\) with accuracy

\displaystyle n = \tilde O\Big(\frac{d^2}{\alpha^2} + \frac{\log(1/\delta)}{\varepsilon} + \frac{d^2}{\alpha \varepsilon}\Big)
\displaystyle \mathbb{E}[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2] \leq \alpha^2

samples

Known algorithmic results

with

(Output of \(\mathcal{M}(X)\) does not change much if switch one \(x_i\))

Our Results - New Lower Bounds

Theorem

For any \((\varepsilon, \delta)\)-DP algorithm \(\mathcal{M}\) such that

\displaystyle \mathbb{E}\big[\lVert\mathcal{M}(X) - \Sigma\rVert_F^2\big] \leq \alpha^2 = O(d)

and

\displaystyle \delta = O\Big( \frac{1}{n \ln n}\Big)

we have

\displaystyle n = \Omega\Big(\frac{d^2}{\alpha\varepsilon}\Big)

Above 1/n, DP may not be meaningful

Previous                   

\displaystyle n = \Omega\big(\tfrac{d^2}{\alpha\varepsilon}\big)

Lower Bounds

\displaystyle \tilde{O}(\tfrac{1}{n})
\displaystyle \delta
\displaystyle O(1)
\displaystyle O(d)

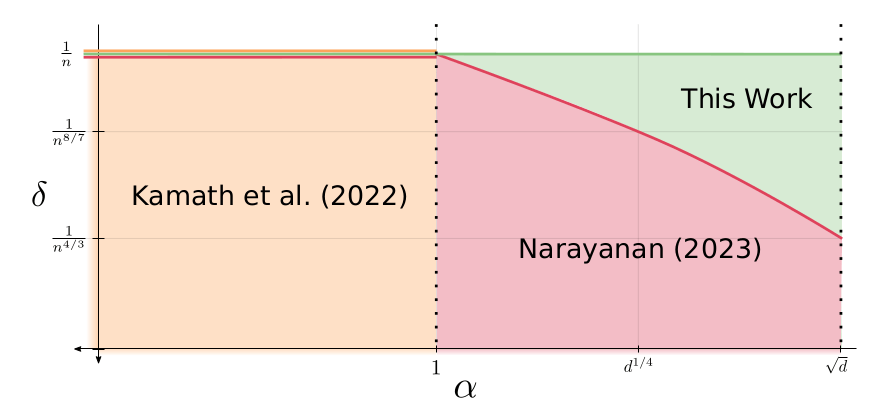
Accuracy  \(\alpha^2\)

New Fingerprinting Lemma using

Stokes' Theorem

Follow up:

LBs for other problems

[Lyu & Talwar ´25]

Lower Bounds via Fingerprinting

Measures correlation between    and         

Correlation statistic

\displaystyle \mathcal{C}(\phantom{z}, \phantom{\mathcal{M}(X)})
\displaystyle \mathbb{E}[|\mathcal{C}(z, \mathcal{M}(X))|]

If \(z \sim \mathcal{N}(0, \Sigma)\) indep. of \(X\)

small

\displaystyle \mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]

If \(\mathcal{M}\) is accurate

large

Fingerprinting Lemma

Approx. equal by privacy

Approx. equal by privacy

z
z
\mathcal{M}(X)
\mathcal{M}(X)
\displaystyle \Sigma
\displaystyle zz^{\intercal}
\displaystyle zz^{\intercal}
\displaystyle zz^{\intercal}
\displaystyle zz^{\intercal}
\displaystyle \mathcal{M}(X)
\displaystyle \Sigma
\displaystyle x_3 x_3^{\intercal}
\displaystyle x_1 x_1^{\intercal}
\displaystyle x_2 x_2^{\intercal}
\displaystyle \mathcal{M}(X)

Example:

\displaystyle \mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle

Randomizing \(\Sigma\)

To get a FP lemma, we need to randomize \(\Sigma\)

How to choose the distribution of \(\Sigma\)?

Narayanan (2023) drops independence with a Bayesian argument 

otherwise, there is \(\mathcal{M}\) that knows \(\Sigma\) and ignores \(X\)

Most FP Lemma take independent coordinates

1 dim. FP Lemma and apply to each coord.

For covariance works only for high-accuracy \(\mathcal{M}\) (Kamath et al. 2022)

\displaystyle \Bigg \{

Our idea: Many FP Lemmas use Stein's identity (Integration by parts)

How to do something similar in high-dimensions?

Score Statistic

\displaystyle \mathcal{C}(z, \mathcal{M}(X)) = \big\langle\mathcal{M}(X) - \Sigma, \mathrm{Score}(z \;|\; \Sigma))\big\rangle

Gaussian Score function

Score Attack Statistic

First step: Pick a different correlation statistic

\displaystyle \mathcal{C}(z, \mathcal{M}(X))

"Usual" choice

\displaystyle \mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
\displaystyle zz^{\intercal}
\displaystyle \mathcal{M}(X)
\displaystyle \Sigma

[Cai et al. 2023]

\displaystyle I
\displaystyle \mathcal{M}(X)
\displaystyle zz^{\intercal}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}

New Fingerprinting Lemma

\(\Sigma \sim\) Wishart leads to elegant analysis

Stein-Haff Identity

Want to "Move the derivative" with integration by parts

Stokes' Theorem

\displaystyle \sum_{j,k} \frac{\partial}{\partial \Sigma_{jk}} \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]
\displaystyle \sum_{i} \mathcal{C}(x_i, \mathcal{M}(X)) =

Divergence of \(\Sigma \mapsto \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\)

Large If \(\mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\approx \Sigma\)

Main property:

\displaystyle = \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle \mathbb{E}\;\Big[ \mathrm{div}\, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] \Big]

\(\Sigma\) is random with density \(p\)

\displaystyle p(\Sigma)
\displaystyle \Sigma \sim p

Summary

Our results

Score Attack Statistic

Tight lower bounds private covariance estimation

over a broad parameter regime

\displaystyle \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle p(\Sigma)
\displaystyle zz^{\intercal}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle I
\displaystyle \mathcal{M}(X)
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}

Stein-Haff Identify

Thanks!

Technical Secret Sauce:

New Fingerprinting Lemma

Lower Bounds for Private Estimation of  

Victor Sanches Portella

July 2, 2025

joint work with Nick Harvey (UBC)

under All Reasonable Parameter Regimes

Gaussian Covariance Matrices

ime.usp.br/~victorsp

Randomizing \(\Sigma\)

To get a FP lemma, we need to randomize \(\Sigma\)

\(\Sigma\) with "small variance" \(\implies\) 

FP Lemma only for high-accuracy \(\mathcal{M}\)

\(\Sigma\) with "large variance" \(\implies\)

hard to upper bound \(\mathbb{E}[|\mathcal{C}(z, \mathcal{M}(X))|]\)                  for independent \(z\)

\displaystyle \mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]

If \(\mathcal{M}\) is accurate

large

Fingerprinting Lemma

\displaystyle \Sigma
\displaystyle x_3 x_3^{\intercal}
\displaystyle x_1 x_1^{\intercal}
\displaystyle x_2 x_2^{\intercal}
\displaystyle \mathcal{M}(X)
\displaystyle \mathcal{M}(X) = \mathbb{E}[\Sigma]

is accurate and ignores \(X\)

otherwise, there is \(\mathcal{M}\) that knows \(\Sigma\) and ignores \(X\)

Randomizing \(\Sigma\)

\displaystyle I
\displaystyle \mathcal{M}(X)
\displaystyle zz^{\intercal}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma
\displaystyle p(\Sigma)

New Fingerprinting Lemma

\(\Sigma \sim\) Wishart leads to elegant analysis

Stein-Haff Identity

Want to "Move the derivative" with integration by parts

\displaystyle = \int ( \mathrm{div} \, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] )\, \phantom{p(\Sigma)} \mathrm{d}\Sigma

Stokes' Theorem

\displaystyle \sum_{i = 1}^n \mathbb{E}[\mathcal{C}(x_i, \mathcal{M}(X))]
\displaystyle \geq \Omega(d^2)
\displaystyle O(n \alpha \varepsilon) \geq

FP Lemma

Upper Bound

\displaystyle \mathbb{E}\;\Big[ \mathrm{div}\, \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma] \Big]

\(\Sigma\) is random with density \(p\)

\displaystyle p(\Sigma)
\displaystyle \Sigma \sim p

Score Statistic

\displaystyle \mathcal{C}(z, \mathcal{M}(X)) = \big\langle\mathcal{M}(X) - \Sigma, \mathrm{Score}(z \;|\; \Sigma))\big\rangle

Gaussian Score function

Score Attack Statistic

First step: Pick a different correlation statistic

\displaystyle \mathcal{C}(z, \mathcal{M}(X))

"Usual" choice

\displaystyle \mathcal{C}(z, \mathcal{M}(X)) = \langle\mathcal{M}(X) - \Sigma, z z^{\intercal} - \Sigma \rangle
\displaystyle zz^{\intercal}
\displaystyle \mathcal{M}(X)
\displaystyle \Sigma
\displaystyle \sum_{j,k} \frac{\partial}{\partial \Sigma_{jk}} \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]
\displaystyle \sum_{i} \mathcal{C}(x_i, \mathcal{M}(X)) =

Divergence of \(\Sigma \mapsto \mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\)

Large If \(\mathbb{E}[\mathcal{M}(X) \; | \; \Sigma]\approx \Sigma\)

Main property:

\displaystyle I
\displaystyle \mathcal{M}(X)
\displaystyle zz^{\intercal}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}
\displaystyle \Sigma^{-1/2}