An Alternative to EM for Gaussian Mixture Models

Victor Sanches Portella
MLRG @ UBC

August 11, 2021

Why this paper?

Interesting application of Riemannian optimization to an important problem in ML

Details of the technicalities are not important

Yet, we have enough to sense the flavor of the field

Gaussian Mixture Models

Gaussian Mixture Models

A GMM is a convex combination of a fixed number of Gaussians

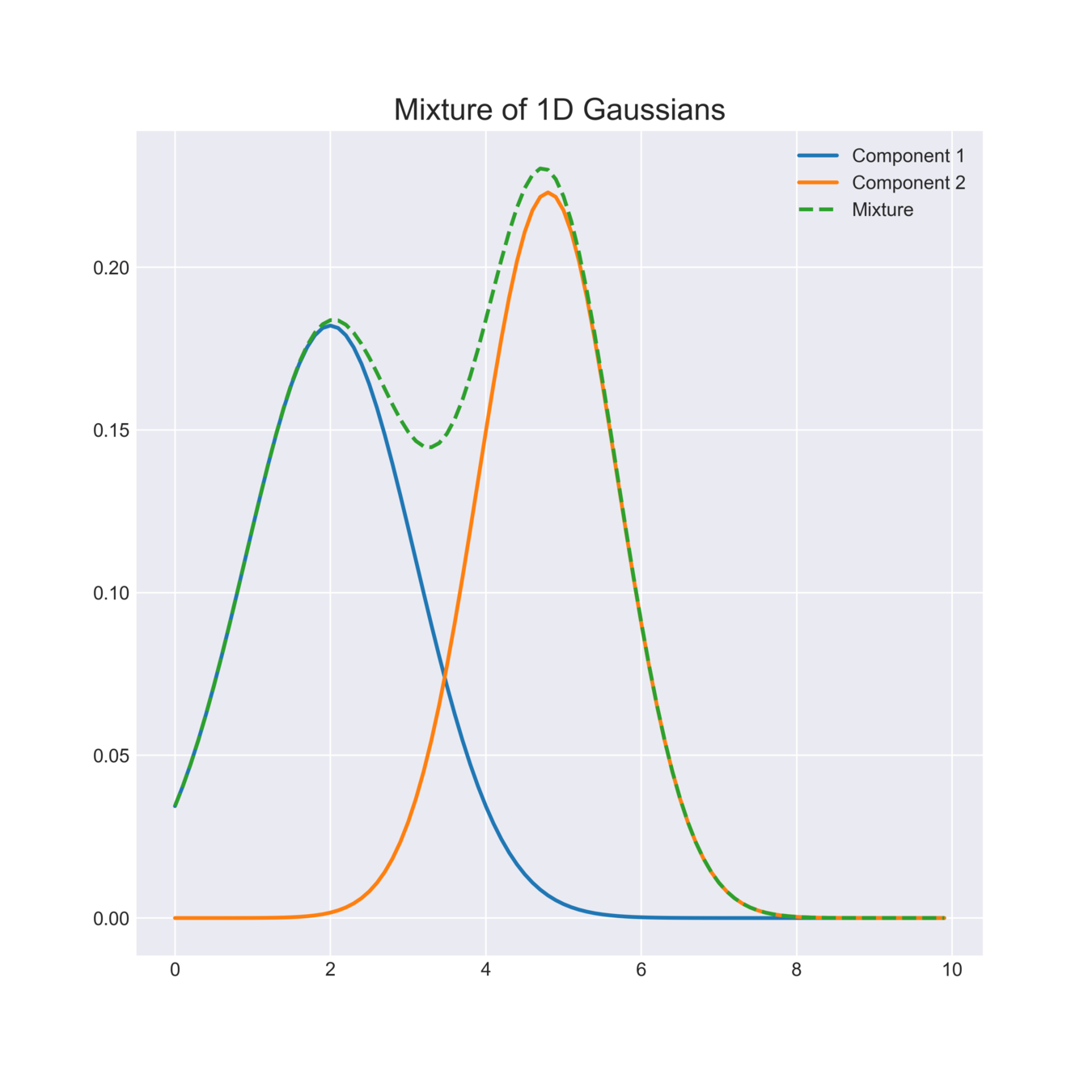
Image source: https://angusturner.github.io/assets/images/mixture.png

Gaussian Mixture Models

A GMM is a convex combination of a fixed number of Gaussians

Density of a \(K\)-mixture on \(\mathbb{R}^d\):

\displaystyle p(x) = \sum_{i = 1}^K \alpha_i \; p_{\mathcal{N}}(x; \mu_i, \Sigma_i)

Mean and Covariance of \(i\)-th Gaussian

Gaussian density

Weight of \(i\)-th Gaussian

(Must sum to 1)

Find GMM  most likely to generate data points  \(x_1, \dotsc, x_n \)

Fitting a GMM

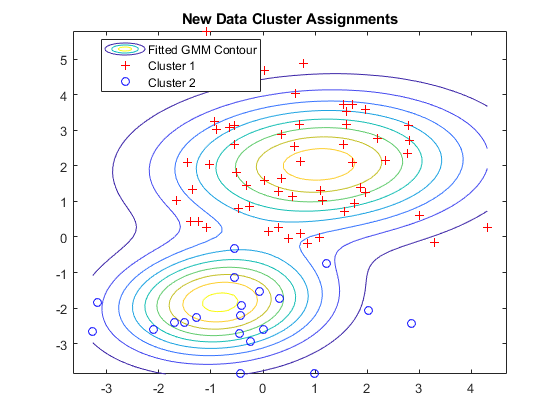
Image source: https://towardsdatascience.com/gaussian-mixture-models-d13a5e915c8e

Find GMM  most likely to generate data points  \(x_1, \dotsc, x_n \)

Fitting a GMM

Idea: use means \(\mu_i\) and covariances \(\Sigma_i\) that maximize log-likelihood

\displaystyle \max \sum_{i = 1}^n \log\Big(\sum_{j = 1}^K \alpha_i \; p_{\mathcal{N}}(x_i; \mu_j, \Sigma_j)\Big)
\displaystyle \sum_{i = 1}^n
\displaystyle x_i
\{
\alpha \in \Delta_n
\mu_j \in \mathbb{R}^d
\Sigma_j \succ 0
\Sigma_j \succ 0

Hard to describe

Open - No clear projection

Classical optimization methods (Newton, CG, IPM) struggle

Optimization vs "\(\succ 0\)"

Slowdown when iterates get closer to boundary

IPM works, but it is slow

Force positive definiteness via "Cholesky decomposition"

Adds spurious maxima/minima

\Sigma = L L^T

Slow

Expectation Maximization guarantees \(\succ 0\) "for free"

Easy for GMM's

Fast in practice

EM: Iterative method to find (local) max-likely parameters

EM in one slide

E-step: Fix parameters, find "weighted log-likelihood"

M-step: Find parameters by maximizing the "weighted log-likelihood"

For GMM's:

E-step: Given \(\mu_i, \Sigma_i\), compute \(P(x_j \in \mathcal{N}_i)\)

M-step: Max weighted log-likelihood with weights \(P(x_j \in \mathcal{N}_i)\)

\(= p(x_j ; \mu_i, \Sigma_i)\)

CLOSED FORM SOLUTION FOR GMMs!

Guarantees \(\succ 0\) for free

Riemannian Optimization

Manifold of PD Matrices

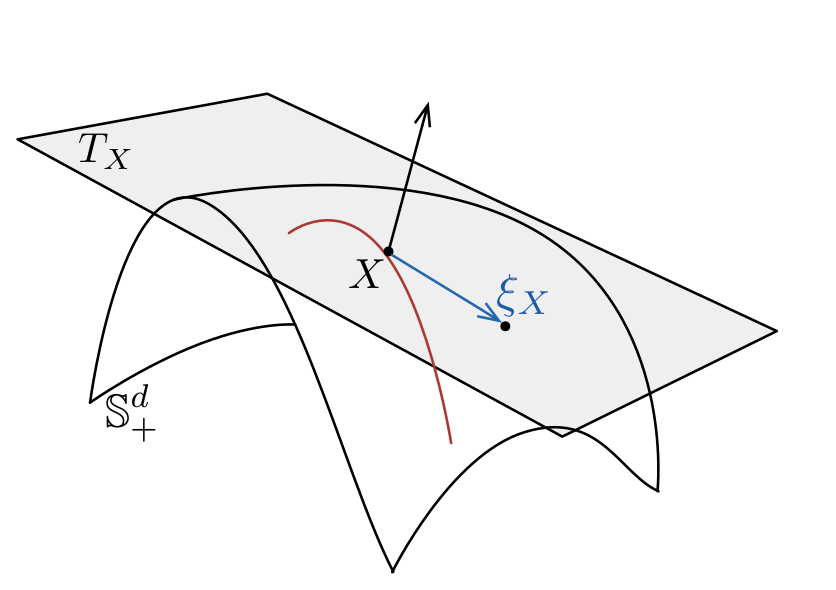
Manifold of PD Matrices

\mathbb{P}^d = \{\Sigma \in \mathbb{R}^{d \times d} \colon \Sigma \succ 0\}

Rimennian metric at

\Sigma
\langle X,Y \rangle_{\Sigma} = \mathrm{Tr}(\Sigma^{-1} X \Sigma^{-1} Y)
\Sigma

Tangent space           at a point

T_{\Sigma}
\equiv

All symmetric matrices

Remark: Blows up when \(\Sigma\) is close to the boundary

Optimization Structure

General steps:

1 - Find descent direction

2 - Perform line-search and step with retraction

Retraction: a way to move on a manifold along a tangent direction

\mathrm{Ret}_{\Sigma} \colon T_{\Sigma} \to \mathbb{P}^d
\mathrm{Ret}_{\Sigma}(0) = \Sigma
\mathrm{D Ret}_{\Sigma}(0) = \mathrm{Id}
\{

Not necessarily follows a geodesic!

\mathrm{D}

In this paper, we will only use the Exponential Map:

\mathrm{Ret}_{\Sigma}(D) = \gamma_D(1)

where

\gamma_D(t)

is the geodesic starting at \(\Sigma\) with direction \(D\)

The Exponential Map

\mathrm{Ret}_{\Sigma}(D) = \gamma_D(1)

where

\(\gamma_D(t)\) is the geodesic starting at \(\Sigma\) with direction \(D\)

Geodesic between \(\Sigma\) and \(\Gamma\)

 \(\Sigma\) at \(t = 0\) and \(\Gamma\) at \(t = 1\)

\Sigma^{\frac{1}{2}} (\Sigma^{-\frac{1}{2}} \Gamma \Sigma^{-\frac{1}{2}})^t \Sigma^{\frac{1}{2}}
\displaystyle (
\displaystyle )^{}
{}^t

From this (?), we get the form of the exponential map

\mathrm{Ret}_{\Sigma}(D) = \Sigma^{\frac{1}{2}} \exp(\Sigma^{-\frac{1}{2}} D \Sigma^{-\frac{1}{2}}) \Sigma^{\frac{1}{2}}
= \Sigma \; \exp(\Sigma^{-1} D )

Gradient Descent

GD on the Riemannian Manifold \(\mathbb{P}^d\):

\Sigma_{t+1} = \mathrm{Ret}_{\Sigma_t}( - \eta_t \; \mathrm{grad} f(\Sigma_t) )
\mathrm{grad} f(\Sigma_t)
\mathrm{grad} f(\Sigma_t)
\equiv

Riemannian gradient of \(f\).

Depends on the metric!

\displaystyle = \frac{1}{2} \Sigma_t \Big(\nabla f(\Sigma_t) + \nabla f(\Sigma_t)^T \Big) \Sigma_t

If we have time, we shall see conditions for convergence of SGD

The methods the authors use are Conjugate Gradient and LBFGS.

x_{t+1} = x_t - \eta_t \nabla f(x_t)

Traditional gradient descent (GD):

Defining those depends on the idea of vector transport and Hessians. I'll skip these descriptions

Riemannian opt for GMMs

We have a geometric structure on \(\mathbb{P}^d\). The other variable can stay in the traditional Euclidean space.

We can apply methods for Riemannian optimization!

... but they are way slower than traditional EM

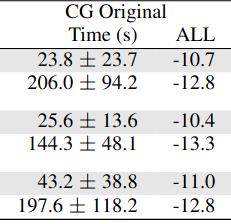
GMMs and Geodesic Convexity

Single Gaussian Estimation

Maximum Likelihood estimation for a single Gaussian:

\displaystyle \max_{\mu, \; \Sigma \succ 0} \mathcal{L}(\mu, \Sigma) \coloneqq \sum_{i = 1}^n \log p_{\mathcal{N}}(x_i; \mu, \Sigma)

\(\mathcal{L}\) is concave!

In fact, the above has a closed form solution

In a Riemannian manifold, meaning of convexity changes

Geodesic convexity (g-convexity):

f(\gamma(t)) \leq (1 - t) f(\Sigma_1) + t f(\Sigma_2)
\gamma(t)

Geodesic from \(\Sigma_1\) to \(\Sigma_2\)

\(\mathcal{L}\) is not g-concave

Single Gaussian Estimation

Maximum Likelihood estimation for a single Gaussian:

\displaystyle \max_{\mu, \; \Sigma \succ 0} \mathcal{L}(\mu, \Sigma) \coloneqq \sum_{i = 1}^n \log p_{\mathcal{N}}(x_i; \mu, \Sigma)

\(\mathcal{L}\) is concave!

\(\mathcal{L}\) is not g-concave

Solution: lift the function to a higher dimension!

\displaystyle \max_{S \succ 0} \hat{\mathcal{L}}(S) \coloneqq \sum_{i = 1}^n \log q_{\mathcal{N}}(y_i; S)
\displaystyle = \begin{pmatrix} x_i \\ 1 \end{pmatrix}
(d + 1) \times (d+1)

\(\hat{\mathcal{L}}\) is g-concave

\displaystyle = c \cdot p_{\mathcal{N}}(y_i; 0, S)

Single Gaussian Estimation

\displaystyle \max_{\mu, \; \Sigma \succ 0} \mathcal{L}(\mu, \Sigma) \coloneqq \sum_{i = 1}^n \log p_{\mathcal{N}}(x_i; \mu, \Sigma)
\displaystyle \max_{S \succ 0} \hat{\mathcal{L}}(S) \coloneqq \sum_{i = 1}^n \log q_{\mathcal{N}}(y_i; S)

Theorem If \(\mu^*, \Sigma^*\) max \(\mathcal{L}\) and \(S^*\) maxs \(\hat{\mathcal{L}}\), then

\(\mathcal{L}\) is not g-concave

\(\hat{\mathcal{L}}\) is g-concave

\displaystyle \mathcal{L}(\mu^*, \Sigma^*) = \hat{\mathcal{L}}(S^*)
S^* = \begin{pmatrix} \Sigma^* + \mu^* {\mu^{*}}^T & \mu^* \\ \mu^* & 1 \end{pmatrix}

and

Theorem If \(\mu^*, \Sigma^*\) max \(\mathcal{L}\) and \(S^*\) maxs \(\hat{\mathcal{L}}\), then

\displaystyle \mathcal{L}(\mu^*, \Sigma^*) = \hat{\mathcal{L}}(S^*)
S^* = \begin{pmatrix} \Sigma^* + \mu^* {\mu^{*}}^T & \mu^* \\ \mu^* & 1 \end{pmatrix}

and

Proof idea:

S = \begin{pmatrix} \Sigma + s \mu {\mu}^T & s \mu \\ s \mu & s \end{pmatrix}
s > 0

Write

Optimal choice of \(s\) is 1 \(\implies\) both \(\mathcal{L}\) and \(\hat{\mathcal{L}}\) agree

PS: \(\Sigma^* \succ 0\) by Shur's complement Lemma

Back to Many Gaussians

\displaystyle \max \mathcal{L}\big(\{\mu_j\}, \{\Sigma_j\} \big) = \sum_{i = 1}^n \log\Big(\sum_{j = 1}^K \alpha_i \; p_{\mathcal{N}}(x_i; \mu_j, \Sigma_j)\Big)

For now, fix

\alpha_1, \dotsc, \alpha_k
\displaystyle \max \hat{\mathcal{L}}\big(\{S_j\} \big) = \sum_{i = 1}^n \log\Big(\sum_{j = 1}^K \alpha_i \; q_{\mathcal{N}}(y_i; S_j)\Big)

Theorem The local maxima of \(\mathcal{L}\) and of \(\hat{\mathcal{L}}\) agree

What about \(\alpha_1, \dotsc, \alpha_K\)? Reparameterize to use unconstrained opt

\displaystyle \alpha_j \coloneqq \frac{\exp(w_j)}{\sum_{k = 1}^K \exp(w_k)}

I think there are not many guarantees on final \(\alpha_j\)'s

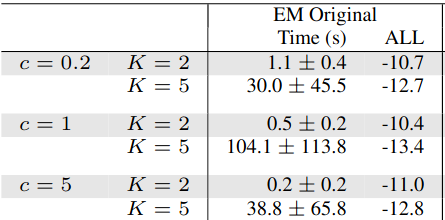
Plots!

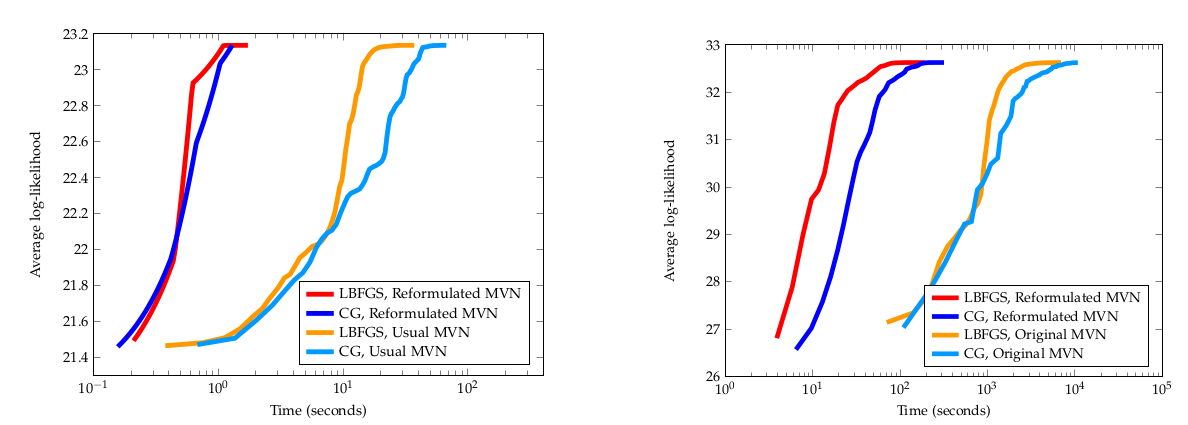
The effect of the lifting on convergence

Plots!

EM vs Riemannian Opt

K = 3
K = 7

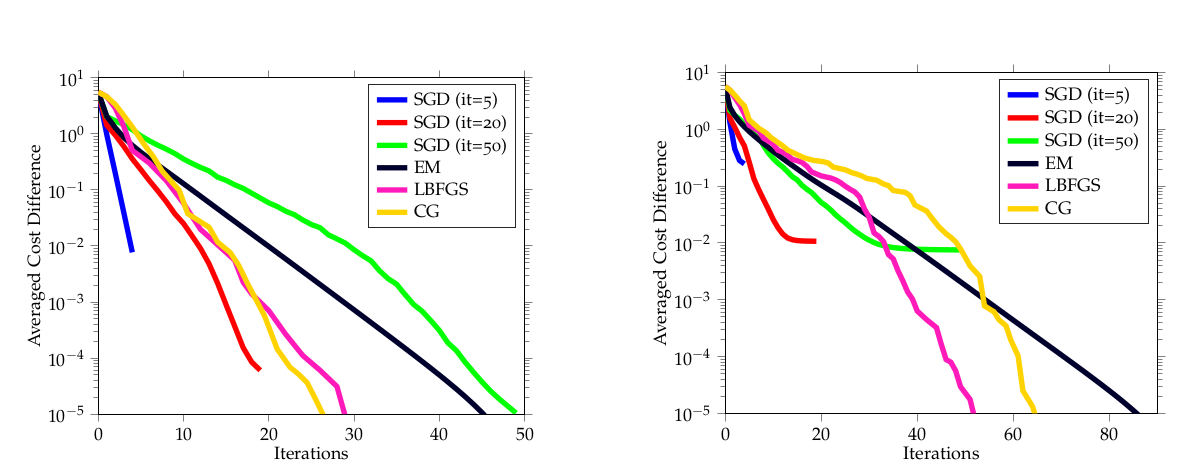
PS: Reformulation helps Cholesky as well, but this information disappeared from the final version

Remarks on What I Skipped

Step-size Line Search

Lifting with Regularization

Details on vector transport and 2nd order methods

Riemannian SGD

Riemannian SGD

x_{t+1} = \mathrm{Ret}_{x_t}\big(- \eta_t \; \mathrm{grad} f_{i_t}(x_t)\big),

\(i_t\) a random index

Assumptions on \(f\):

Riemann Lip. Smooth

f\big(\mathrm{Ret}_{x}(d)\big) \leq f(x) + \langle \mathrm{grad} f(x), d \rangle + \frac{L}{2} ||d ||^2

Unbiased Gradients

\mathbb{E}[ \mathrm{grad} f_{i_t}(x) - \mathrm{grad} f(x)] = 0

Bounded Variance

\mathbb{E}\big[ ||\mathrm{grad} f_{i_t}(x) - \mathrm{grad} f(x)||^2\big] \leq \sigma

We want to minimize

f = \frac{1}{n} \sum_{i = 1}^n f_i

Riemannian Stochastic Gradient Descent:

Riemannian SGD

x_{t+1} = \mathrm{Ret}_{x_t}\big(- \eta_t \; \mathrm{grad} f_{i_t}(x_t)\big)

Assumptions on \(f\):

Riemann Lip. Smooth

Unbiased Gradients

Bounded Variance

f = \frac{1}{n} \sum_{i = 1}^n f_i

Riemannian SGD

Theorem If one of the following holds:

i) Bounded gradients:

|| \mathrm{grad} f(x)|| \leq G \quad \forall i

ii) Outputs an uniformly random iterate

Then

\displaystyle \mathbb E \Big[ || \mathrm{grad} f(x_{\tau})||^2 \Big] \leq O\Bigg(\frac{1}{\sqrt{T}}\Bigg),

\(\tau\) is unif. random if (ii)

\(\tau\) is best iter. if (i)

(No need for bdd var)

Does SGD work for GMM?

Do the conditions for SGD to converge hold for GMMs?

Theorem If \(\eta_t \leq 1\), then iterates stay in a compact set.

(For some reason they analyze SGD with a different retraction...)

Remark Objective function is not Riemannian Lip. smooth outside of a compact set

Fact Iterates stay in a compact set \(\implies\)

Bounded Gradients

\(\implies\)

Classical Lip. smoothness

\(\implies\)

Thm from Riemannian Geometry

Riemann Lip. smoothness

It works!

With a different retraction and at a slower rate...?

Made with Slides.com