35o Colóquio Brasileiro de Matemárica

for the Distinct Elements Problem

Privacy Guarantees

Intrinsic

Stable Random Projections

of

Victor Sanches Portella

July, 2025

ime.usp.br/~victorsp

Joint work with Nick Harvey and Zehui (Emily) Gong

Privacy? Why, What, and How

What do we mean by "privacy" in this case?

Informal Goal: Output should not reveal (too much) about any single individual

Different from security breaches (e.g., server invasion)

Output

Data Analysis

Trivial if output does not need to have information about the population

Real-life example - Netflix Dataset

Differential Privacy

Anything learned with an individual in the dataset

can (likely) be learned without

\displaystyle \mathcal{M}
\displaystyle \mathcal{M}

Indistinguishible

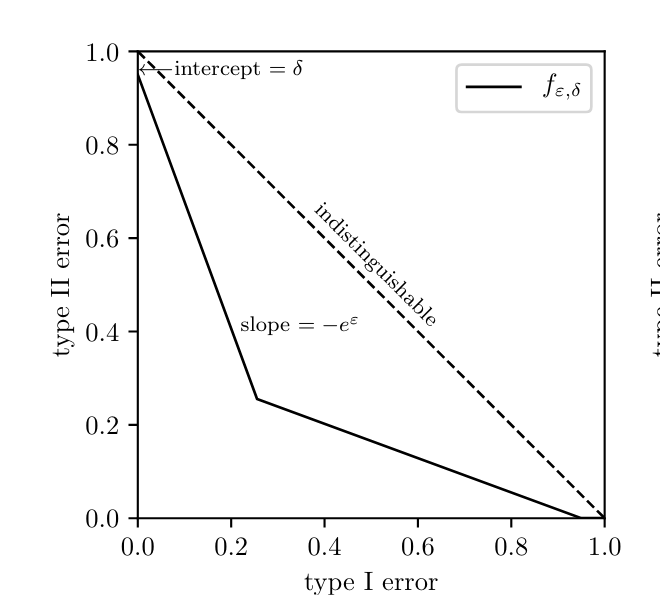
Differential Privacy (Formally)

Any pair of neighboring datasets: they differ in one entry

\(\mathcal{M}\) is \((\varepsilon, \delta)\)-Differentially Private if

\mathbb{P}(\mathcal{M}(X) \in S) \leq e^{\varepsilon} \cdot \mathbb{P}(\mathcal{M}(X') \in S) + \delta

Definition:

\forall S

\((\varepsilon, \delta)\)-DP

\(\varepsilon \equiv \)  "Privacy leakage", constant (in theory \(\leq 1\))

\(\delta \equiv \)  "Chance of catastrophic privacy leakage"

                     usually \(\ll 1/|X|\)

\displaystyle \Bigg \{

Definition is a bit cryptic, but implies limit on power of hypothesis test of an adversary

\(\mathcal{M}\) needs to be randomized to satisfy DP

Interpretation of DP: Hard to Hypothesis Test

\(H_0:\) Output is from \(\mathcal{M}(X)\)

\(H_1:\) Output is from \(\mathcal{M}(X')\)

Some Advantages of Differential Privacy

Worst case: No assumptions on the adversary

Composable: DP guarantees compose nicely

Loose!

\mathcal{M}_1
\mathcal{M}_2

\((\varepsilon_1, \delta_1)\)-DP

\((\varepsilon_2, \delta_2)\)-DP

\(\implies\)

Both together are

\((\varepsilon_1 +\varepsilon_2, \delta_1 + \delta_2)\)-DP

A Few Topics I am Interested in DP

Learning Theory

Deep Ideas in Lower Bounds via Fingerprinting

Proof uses Ramsey's Theory

We are starting work on this

In this Talk: Revisiting Randomized Algorithms

Ongoing extension to optimization problems

Counting Distinct Elements

Counting Distinct Elements in a Stream

The problem:

Count (approx.) the number of distinct elements in a stream of \(N\) items of \(n\) types

Want to use \(o(n)\) space

Example: Counter of # of listeners of a song

Items arrive sequentially 

\(N\) and \(n\) are LARGE

[Pokemon Icons by Roundicon Freebies at flaticon.com]

Distinct Elements via Sketching

Frequency vector \(f(x)\) of size \(n\)

Stream \(x\) of length \(N\)

3

2

1

1

Instead, use Small sketch

Allow us to track 

# distinct elements of \(x\)
in small space

Stable Random Projections

Warm-up: Estimating the \(F_2\) norm 

Goal:

Estimate \(\lVert f(x)\rVert_2^2 = f(x)_1^2 + f(x)_2^2 + \dotsm + f(x)_n^2\) of a stream \(x\)

3

2

1

1

2

2

2

2

+

+

+

\(\mathbb{E}\big [(Z^{\mathsf{T}} f(x))^2\big]=  \lVert f(x)\rVert_2^2\) 

but \(Z^{\mathsf{T}} f(x)\)  maybe far from its expectation

Solution: Repeat \(r\) times and take the average

Key observation:

If \(Z \sim \mathcal{N}(0,I)\), then \(Z^{\mathsf{T}} f(x) \sim \mathcal{N}(0, \lVert f(x)\rVert_2^2\)) 

Warm-up: Estimating the \(F_2\) norm 

\(r \times n\) Gaussian matrix

\(f(x)\)

\(=\)

\(\mathsf{sk}(x)\)

Sketch of size \(r\) to approximate \(\lVert f(x)\rVert_2^2\)

Matrix is too large

For each new item, we only need one column of the matrix

We can generate this matrix implicitly with low space using

pseudorandom generators

(Closely related to Johnson–Lindenstrauss)

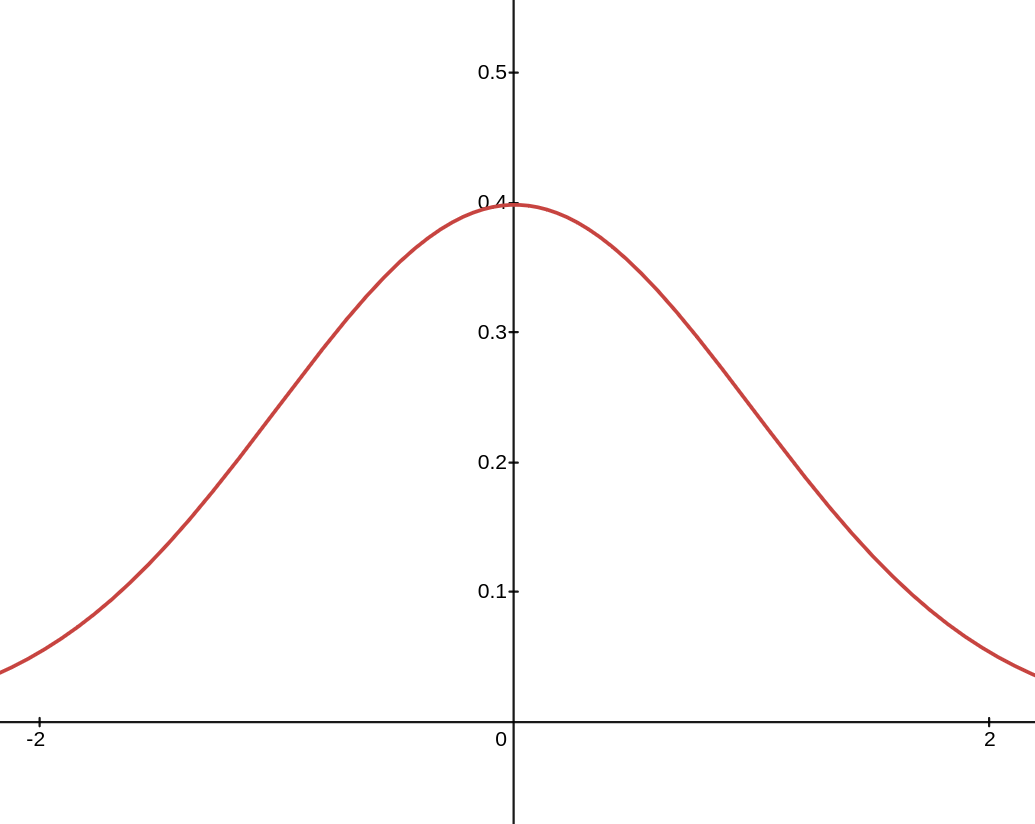
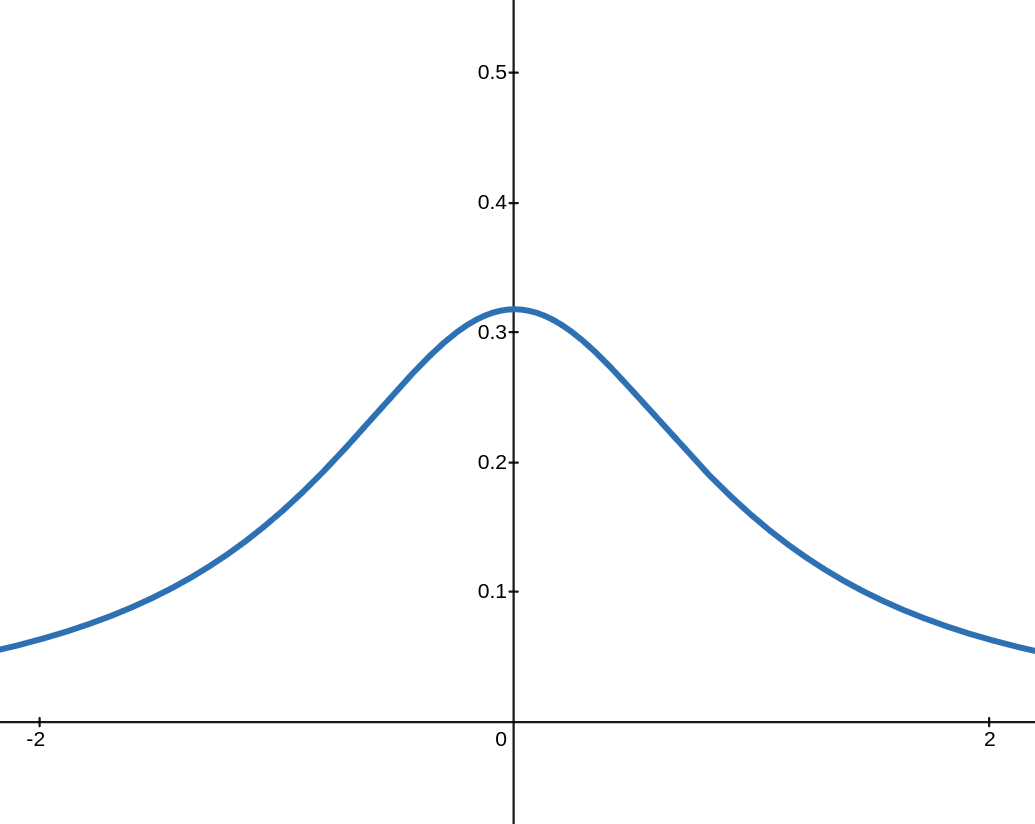
Stable Distributions

Stability of Gaussians:

a Z + b Y \sim (a^2 + b^2)^{1/2} \cdot \mathcal{N}(0,1)

If \(Z,Y \sim \mathcal{N}(0,1)\) are independent

a Z + b Y \sim (a^{\phantom{p}} + b^{\phantom{p}})^{1/\phantom{p}} \cdot \mathcal{D}_p

\(p\)-Stable Distribution \(\mathcal{D}_p\):

If \(Z,Y \sim \mathcal{D}_p\) are independent,

{}^{p}
{}^{p}
{}^{p}

Gaussian (\(p = 2\))

Cauchy (\(p = 1\))

Stable Projections

\(r \times n\)

 \(p\)-Stable Matrix

\(f(x)\)

\(=\)

\(\mathsf{sk}(x)\)

Skecth of size \(r\) to approximate \(\lVert f(x)\rVert_p^p\)

For \(p\) small (\(p \leq 1/\lg n\)), \(\lVert f(x)\rVert_p^p \approx\) # distinct elements

Supports removals in the stream

Different sketches can be combined

3

2

1

1

\(p\)

\(p\)

\(p\)

\(p\)

+

+

+

Intrinsic Privacy of
Random Projections

Intrinsic DP Guarantees of Randomized Algorithms

Do some randomized algorithms intrinsically enjoy
privacy guarantees?

Usually, we inject noise/randomness into an algorithm to get DP Guarantees

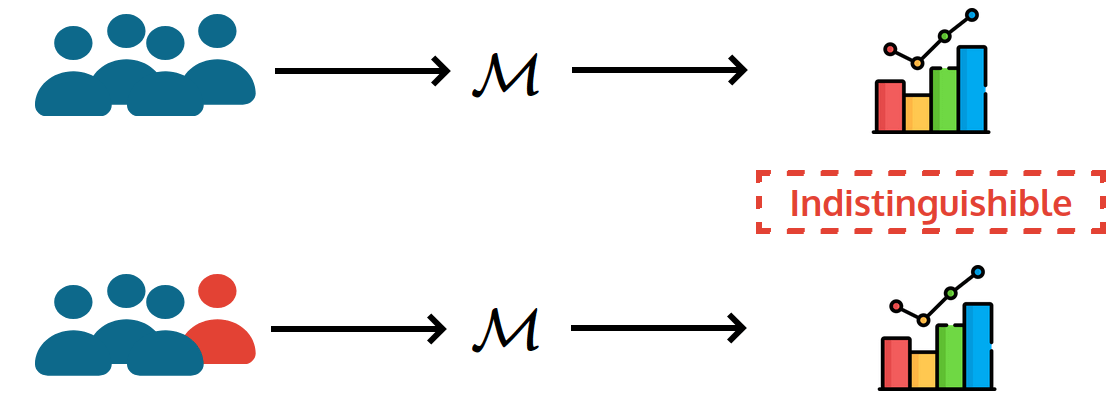
But many algorithms are already randomized!

Neighboring inputs =

exchange one entry in the stream

DP Guarantees of Stable Projections

\mathcal{M}(x) = Z^{\mathsf{T}}f(x)

What are the privacy guarantees of random projections when sketch size is 1?

\(p\)-stable random vector

\(p = 2\)

[Blocki, Blum, Datta, Sheffet ´12]

If \(\lVert f(x) \rVert_2^2 \geq 2 \log(1/\delta)/\varepsilon\) we get \((\varepsilon, \delta)\)-DP

\(p \in (0,1]\)

\(\mathcal{M}\) is \((\Theta(1/p),0 )\)-DP

Pure DP!

Guarantee blows up for \(p \to 0\)

Unclear accuracy guarantees

[Wang, Pinelis, Song 21']

DP Guarantees of \(p\)-Stable for Small \(p\)

Our results:

\((\varepsilon,0 )\)-DP guarantees even for \(p\) small

(Work in progress)

Follows from improving analysis of previous work

\mathcal{M}(x) = Z^{\mathsf{T}}f(x)

\(p\)-stable random vector

Can we do better if  we allow \(\delta > 0\)?

If number of distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)

\(\implies \mathcal{M}\) is \((\varepsilon,0)\)-DP

DP Guarantee:

Beyond \(\delta = 0\): Approximating the Density

Showing DP guarantees boils down to bounding the ratio of densities with different variances

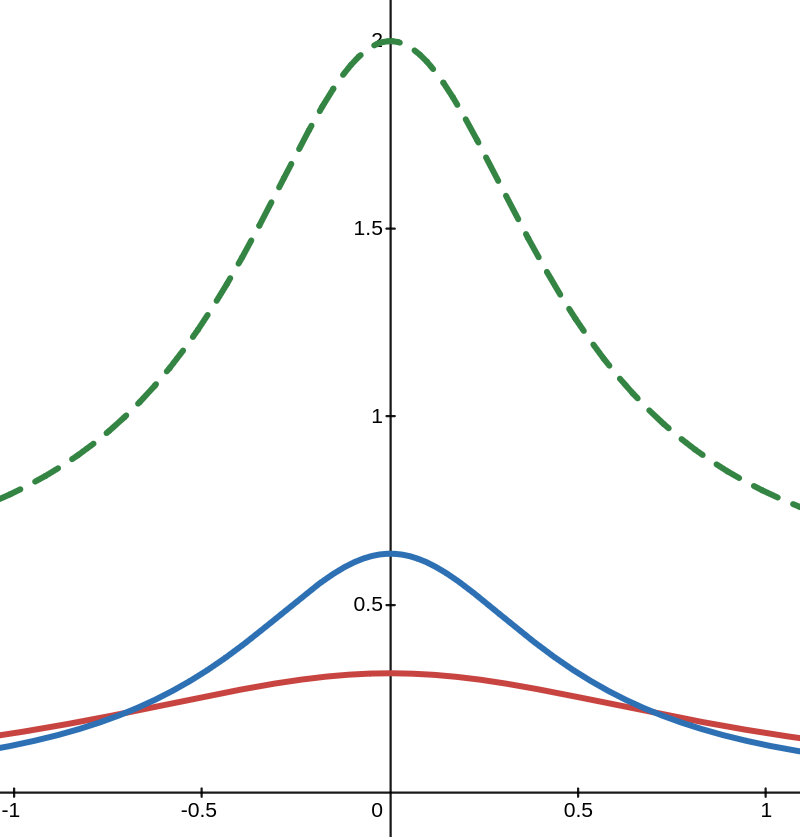
Issue: no closed form for the densities

Main tool: Careful non-asymptotic approximations to the density

const. \(\varepsilon\) unconditionally

constant \(\delta\) 

[Emily's MSc Thesis]

\(p \lesssim 1/\lg n\)

\((12, \phantom{0.82})\)-DP

\(0.82\)

Looking at at limit \(p \to 0\)

Behavior at the limit is known:

|\mathcal{D}_{p}|^p \longrightarrow \frac{1}{\mathsf{Exp}(1)}

\((\varepsilon, 0)\)-DP if # distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)

For p-stable

Thus, allowing \((\varepsilon, \delta)\)-DP instead of \((\varepsilon, 0)\)-DP may not give us much

p \to 0

DP Guarantee

"in the limit"

\((\varepsilon, \delta)\)-DP If # distinct elements \(\geq \log (1/\delta)/\varepsilon\)

\(\gtrsim \log (n)/\varepsilon\)

Summary

We maybe able to improve guarantees
but not by much

Details being worked on

Thanks!

Our results: If # distinct elements is not small, estimating with stable projections already satisfies Pure DP

Stable Projections are a classical and effective way to estimate \(F_p\) norms and approximate                                

distinct elements

[This study was financed, in part, by FAPESP, Brasil (2024/09381-1)]

Backup

An Example: Computing the Mean

Goal:

 is small

\mathcal{M}

\((\varepsilon, \delta)\)-DP that approximates the mean:

Algorithm:

\displaystyle \mathcal{M}(x) = \mathrm{Mean}(x) + Z

Gaussian or Laplace noise

X = (x_1, \dotsc, x_n)
x_i \in [-1,1]

with

\mathbb{E}\Big[\lvert \mathcal{M}(X) - \mathrm{Mean}(x)\rvert \Big]

A Peek Into the Analysis 

Showing DP guarantees boils down to bounding the ratio of densities with different variances

\frac{\phantom{\mathcal{D}_{p,1}(\phantom{Z})}}{\mathcal{D}_{p, \Delta}(\phantom{Z})}
\mathcal{D}_{p,1}(\phantom{Z})
Z
Z

Privacy Loss =

Z \sim \mathcal{D}_p

Bounded with probability \(\delta\)

\implies
(\varepsilon, \delta)\text{-DP}

Issue: \(p\)-stable distributions don't have a closed form for the densities

Looking at at limit \(p \to 0\)

Behavior at the limit is known:

|\mathcal{D}_{p}|^p \longrightarrow \frac{1}{\mathsf{Exp}(1)}

\((\varepsilon, 0)\)-DP if # distinct elements \(\geq 1/ \varepsilon p \approx (\log n)/\varepsilon\)

For p-stable

Thus, allowing \((\varepsilon, \delta)\)-DP instead of \((\varepsilon, 0)\)-DP may not give us much

p \to 0

So, what DP guarantees can we get for a random projection using this distribution?

\Big(\frac{1}{\mathsf{Exp}(1)}\Big)^{1/p}

DP Guarantee:

\((\varepsilon, \delta)\)-DP If # distinct elements \(\geq \log (1/\delta)/\varepsilon\)

\(\gtrsim \log (n)/\varepsilon\)