Searching for
Optimal Per-Coordinate Step-sizes with
Victor Sanches Portella

September 2023
cs.ubc.ca/~victorsp
joint with Frederik Kunstner, Nick Harvey, and Mark Schmidt
Multidimensional Backtracking



Theory Student Seminar @ University of Toronto
Gradient Descent and Line Search
Why first-order optimization?
Training/Fitting a ML model is often cast a (uncontrained) optimization problem
Usually in ML, models tend to be BIG
\(d\) is BIG
Running time and space \(O(d)\) is usually the most we can afford
First-order (i.e., gradient based) methods fit the bill
(stochastic even more so)
Usually \(O(d)\) time and space per iteration
Convex Optimization Setting
\(f\) is convex
Not the case with Neural Networks
Still quite useful in theory and practice
More conditions on \(f\) for rates of convergence
\(L\)-smooth
\(\mu\)-strongly convex



Gradient Descent
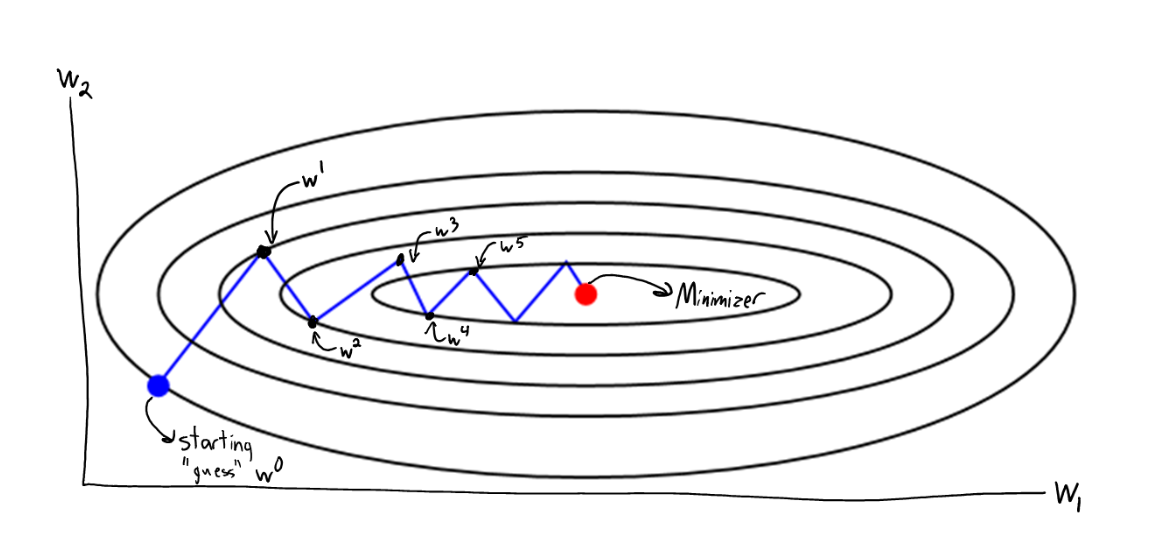
Which step-size \(\alpha\) should we pick?
Condition number
\(\kappa\) Big \(\implies\) hard function
What Step-Size to Pick?
If we know \(L\), picking \(1/L\) always works
and is worst-case optimal
What if we do not know \(L\)?
Locally flat \(\implies\) we can pick bigger step-sizes
If \(f\) is \(L\) smooth, we have
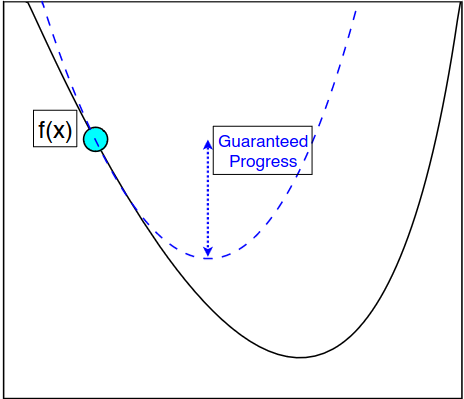
"Descent Lemma"
Idea: Pick \(\eta\) big and see if the "descent condition" holds
(Locally \(1/\eta\)-smooth)
Backtracking Line-Search
Backtracking Line-Search
Start with \(\alpha_{\max} > 2 L\)
\(\alpha \gets \alpha_{\max}/2\)
If
\(t \gets t+1\)
Else
While \(t \leq T\)
Halve candidate space
Guarantee: step-size will be at least \(\tfrac{1}{2} \cdot \tfrac{1}{L}\)
Armijo Condition
Beyond Line-Search?
Converges in 1 step
\(P\)
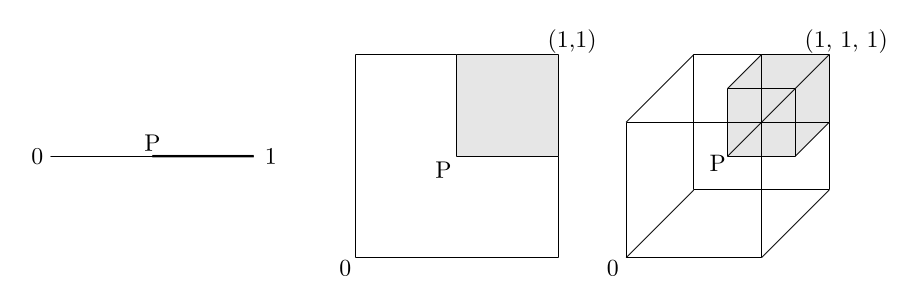
\(O(d)\) space and time \(\implies\) \(P\) diagonal (or sparse)
Can we find a good \(P\) automatically?
"Adapt to \(f\)"
Preconditioer \(P\)
"Adaptive" Optimization Methods
Adaptive and Parameter-Free Methods
Preconditioner at round \(t\)
AdaGrad from Online Learning
or
Better guarantees if functions are easy
while preserving optimal worst-case guarantees in Online Learning
Attains linear rate in classical convex opt (proved later)
But... Online Learning is too adversarial, AdaGrad is "conservative"
In OL, functions change every iteration adversarially
"Fixing" AdaGrad
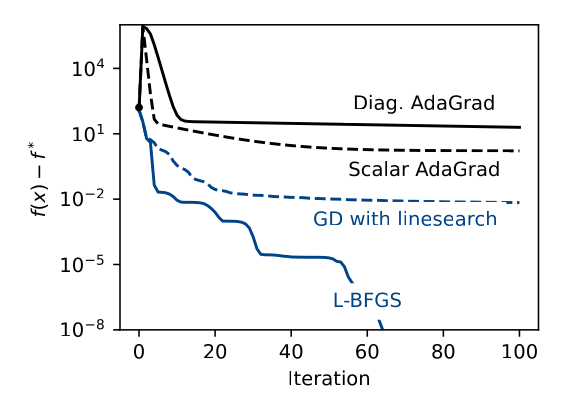
But... Online Learning is too adversarial, AdaGrad is "conservative"
"Fixes": Adam, RMSProp, and other workarounds
"AdaGrad inspired an incredible number of clones, most of them with similar, worse, or no regret guarantees.(...) Nowadays, [adaptive] seems to denote any kind of coordinate-wise learning rates that does not guarantee anything in particular."
Francesco Orabona in "A Modern Introduction to Online Learning", Sec. 4.3

Hypergradient Methods
Idea: look at step-size/preconditioner choice as an optimization problem
Gradient descent on the hyperparameters
How to pick the step-size of this? Well...

Little/ No theory
Unpredictable
... and popular?!
Second-order Methods
Newton's method
is usually a great preconditioner
Superlinear convergence
...when \(\lVert x_t - x_*\rVert\) small
Newton may diverge otherwise
Using step-size with Newton and QN method ensures convergence away from \(x_*\)
Worse than GD
\(\nabla^2 f(x)\) is usually expensive to compute
should also help
Quasi-Newton Methods, e.g. BFGS
State of Affairs
(Quasi-)Newton: needs Hessian, can be slower than GD
Hypergradient methods: purely heuristic, unstable
Online Learning Algorithms: Good but pessimistic theory
at least for smooth optimization it seems pessimistic...
Online Learning
Smooth Optimization
1 step-size
\(d\) step-sizes
(diagonal preconditioner )
Backtracking Line-search
Diagonal AdaGrad
Coordinate-wise
Coin Betting
(non-smooth opt?)
Multidimensional Backtracking
Scalar AdaGrad
Coin-Betting
What does it mean for a method to be adaptive?
Preconditioner Search
Optimal (Diagonal) Preconditioner
Optimal step-size: biggest that guarantees progress
Optimal preconditioner: biggest (??) that guarantees progress
\(L\)-smooth
\(\mu\)-strongly convex
minimizes \(\kappa_*\) such that
Over diagonal matrices
From Line-search to Preconditioner Search
Line-search
step-size is at least \(1/2\) the optimum \(1/L\)
# backtracks \(\leq\)
Multidimensional Backtracking
Condition number is at least \(1/\sqrt{2d}\) the optimum
# backtracks \(\lesssim\)
Worth it if \(\sqrt{2d} \kappa_* \ll 2 \kappa\)
Multidimensional Backtracking
Why Naive Search does not Work
Line-search: test if step-size \(\alpha_{\max}/2\) makes enough progress:
Armijo condition
If this fails, cut out everything bigger than \(\alpha_{\max}/2\)
Preconditioner search:
Test if preconditioner \(P\) makes enough progress:
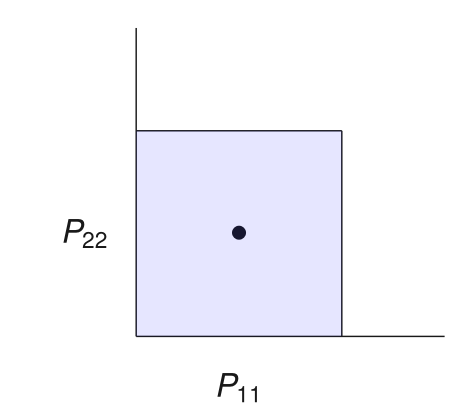
Candidate preconditioners \(\mathcal{S}\): diagonals in a box
If this fails, cut out everything bigger than \(P\)
Why Naive Search does not Work
Preconditioner search:
Test if preconditioner \(P\) makes enough progress:
Candidate preconditioners \(\mathcal{S}\): diagonals in a box
If this fails, cut out everything bigger than \(P\)
Convexity to the Rescue
\(P\) does not yield sufficient progress
Which preconditioners can be thrown out?
All \(Q\) such that \(P \preceq Q\) works, but it is too weak
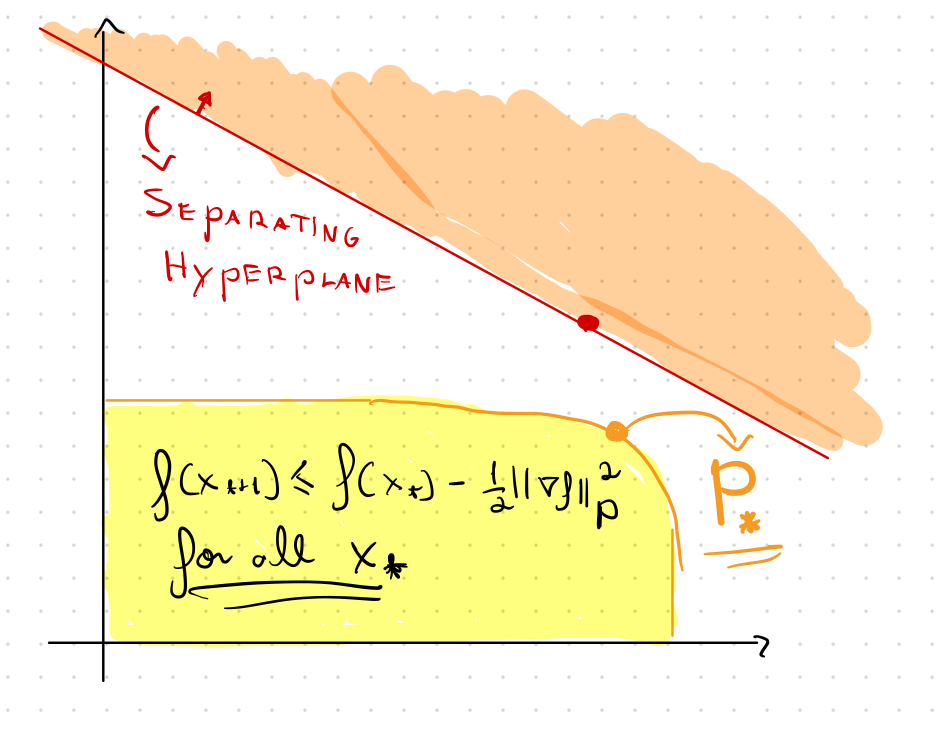
\(P \) does not yield sufficient progress \(\iff\) \(h(P) > 0\)
Convexity \(\implies\)
\(\implies\) \(Q\) is invalid
A separating hyperplane!
\(P\) in this half-space
Hypergradient
Convexity to the Rescue
Box as Feasible Sets
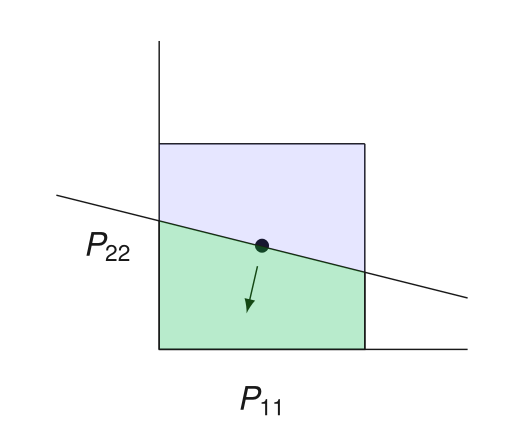
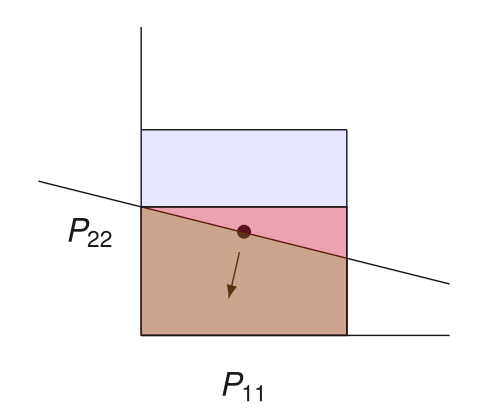
How Deep to Query?
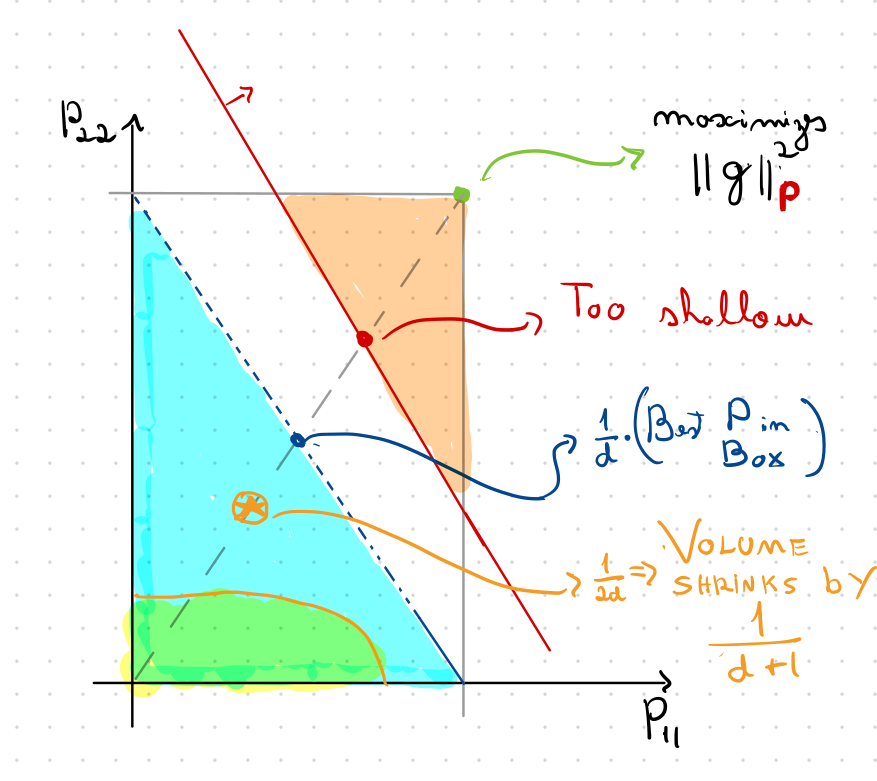
Ellipsoid Method to the Rescue
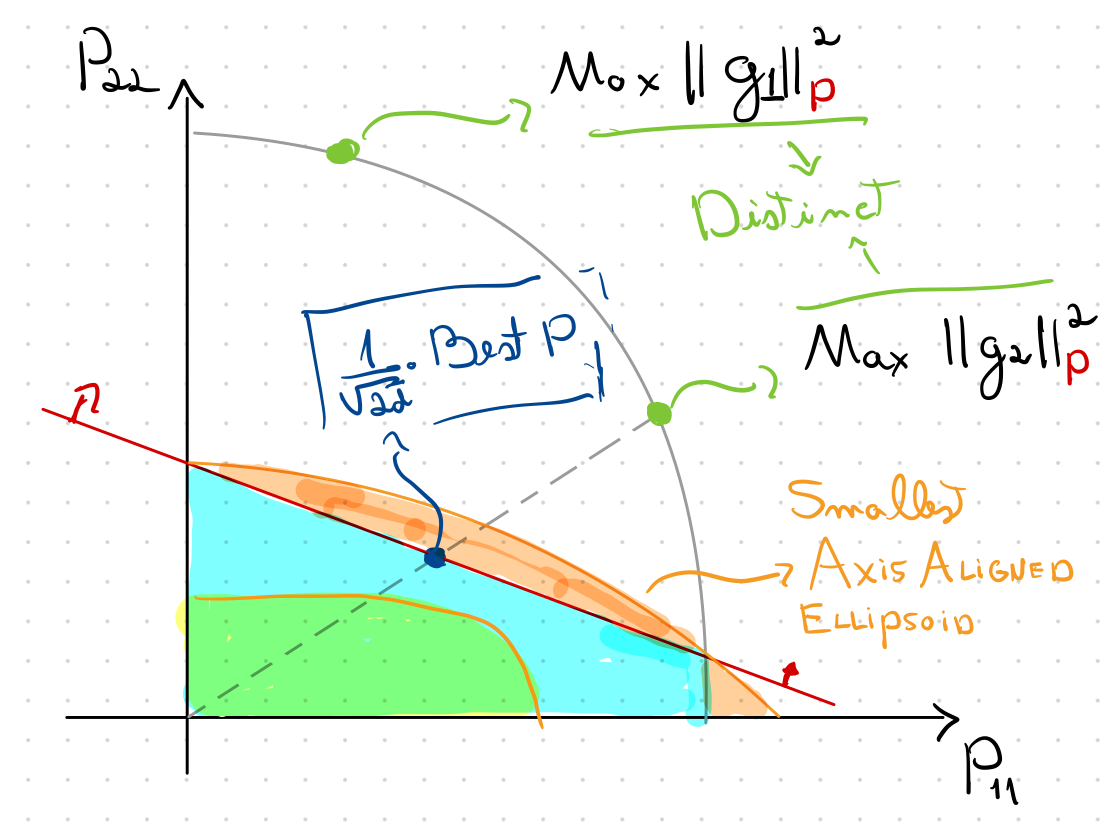
Smallest Axis-Aligned Ellipsoid
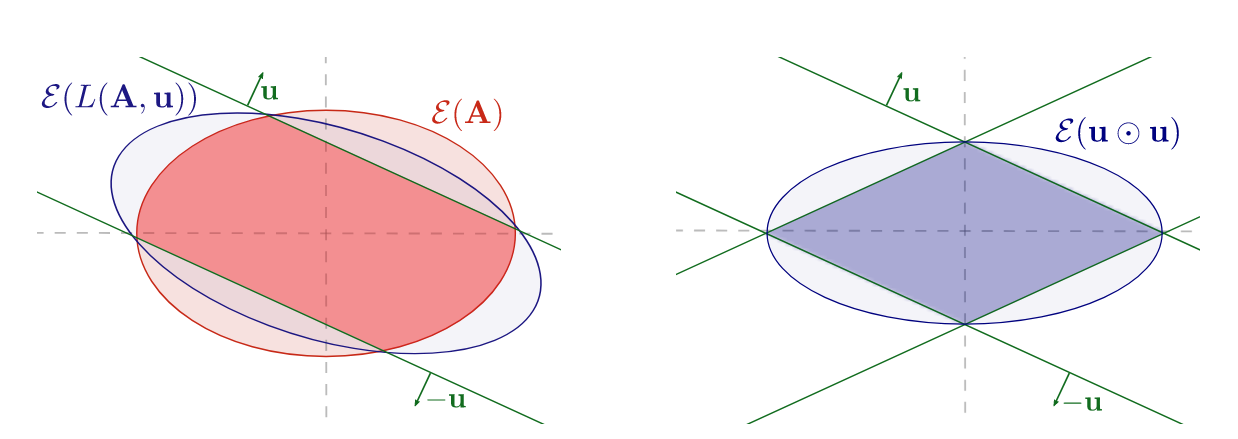
Contraction of \(1/\sqrt{2d}\) from boundary
Constant volume contraction
Conclusions
Theoretically principled adaptive optimization method for strongly convex smooth optimization
A theoretically-informed use of "hypergradients"
ML Optimization meets Cutting Plane methods
Stochastic case?
Heuristics for non-convex case?
Other cutting-plane methods?