Graphs (Contd.)
Overview
- Depth First Search
- Topological Sort using DFS
- Dijkstra Shortest Path Algorithm (single source multiple destination)
- Bellman - Ford Algorithm
DFS
In DFS we take a node and visit its child until we find a dead end in graph.
BFS
In BFS we take node and visit its all adjacent childrens and then move forward
Difference
Similarity
In DFS we traverse through whole graph.
In BFS we traverse through whole graph.
Motivation for DFS
- Edge Classification
- Cycle Detection
- Topological Sorting
Edge Classifiction
Edges are of three type :
- Back Edge : Visiting a parent vertex from a decendent
- Cross Edge : From one tree to the other.
- Forward Edge : visiting a visited vertex from a parent to child
- Tree Edge : An edge vising a new vertex via an edge

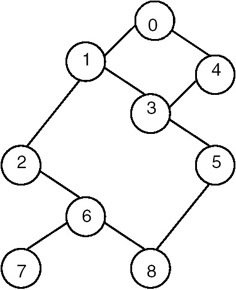
Let's Keep it simple.
you all might have solved maze in past.
Try this one.
Your Entry is from 0 and Exit is at 8
Maze
Steps
- Select a vertex to begin with
- From that vertex consider its neighbor and continue forward
- Again consider the neighbor of the vertex recently discovered
- March forward till you find the dead end
- On dead end turn back and find another possible path
- Do this till all the vertex of a graph are visited.
pseudo-code for selecting a vertex to begin with
DFS()
for vertex in V:
if vertex is not visited
visited[vertex]=true
DFS-Visit(vertex)
DFS-Visit( vertex )
Phase - I
for nodes adjacent to vertex
if( visited[node]==false )
DFS-Visit( node )
Phase - II
Let Dissect It
Step 1:
Select the vertex

Entry : 0
Let Dissect It
Step 2:
Consider its Neighbour

Entry : 0
Let Dissect It
Step 3:
Consider Neighbor's Neighbor

Entry : 0
Let Dissect It
Step 4:
Carry on till all are visited

Entry : 0
Steps for Topological Sort:
- Run DFS on a graph for all vertexes.
- Insert the Vertexes when they are processed in other words during phase - II.
- Present the list in reversed order this a topologically sorted graph.
Problems You can Attempt:
1. UVa 124 - Following Orders
2. UVa 200 - Rare Order
3. UVa 784 - Maze Exploration (Flood Fill) (Special one)
Dijkstra's Algorithm
Task :
To find shortest path from one vertex to another.
What is Shortest Path?
Try yourself:

function Dijkstra(Graph, source):
for each vertex v in Graph: // Initialization
dist[v] := infinity // initial distance from source to vertex v is set to infinite
previous[v] := undefined // Previous node in optimal path from source
dist[source] := 0 // Distance from source to source
Q := the set of all nodes in Graph // all nodes in the graph are un-optimized -
// thus are in Q
while Q is not empty: // main loop
u := node in Q with smallest dist[ ]
remove u from Q
for each neighbor v of u: // where v has not yet been removed from Q.
alt := dist[u] + dist_between(u, v)
if alt < dist[v] // Relax (u,v)
dist[v] := alt
previous[v] := u
return previous[ ]Again Implementing
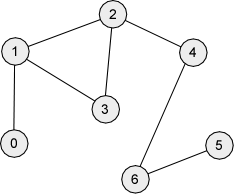
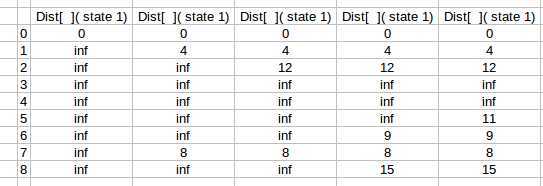
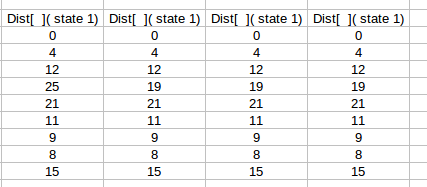
Try the algorithm on the graph given here.

Source : 0
Assumptions:
- G is the set of all the vertexes of the graph that are unprocessed.
- dist[] is array storing distance of any node from a source vertex.
- No negative cycles.
- Infinity is a very large value :P
Step 1 :
Stand at zero and consider all the edges from it to its adjacent vertices.
Step 2 :
Push all the vertex of a graph into a list with distances undefined or infinity.
Step 3 :
Stand at vertex with minimum distance value that is source.
Step 4 :
Get the minimum distance for all the vertex adjacent to it initialized.
Step 5 :
Now get the vertex with minimum value of distance from source from the set G.
Step 6 :
Again, get the minimum distance for all the vertex adjacent to it initialized or updated.
Step 7 :
We get an updated distance array with required output.
Scope of Improvements:
- Using a better means to find minimum from distance array
- Using adjacency list in place of Adjacency Matrix
Problems you can attempt
1. UVa 341 - Non-Stop Travel
2. UVa 929 - Number Maze (on a 2-D maze graph)
3. UVa 10278 - Fire Station
Bellman Ford's Algorithm
Dijkstra
View :
Consider only those vertices with minimum distance or in other words adjacent to the vertex being processed.
Bellman Ford
View :
Consider all the vertices no matter which vertex is being processed.
Benefit :
- Efficient in terms of runtime
Benefit :
- Detect Negative Cycle which dijkstra cannot.
function BellmanFord(list vertices, list edges, vertex source)
// This implementation takes in a graph, represented as
// lists of vertices and edges, and fills two arrays
// (distance and predecessor) with shortest-path
// (less cost/distance/metric) information
// Step 1: initialize graph
for each vertex v in vertices:
if v is source then distance[v] := 0
else distance[v] := inf
predecessor[v] := null
// Step 2: update value of dist array with closer ones
for i in V:
for each edge (u, v) in Graph with weight w in edges:
if distance[u] + w < distance[v]:
distance[v] := distance[u] + w
predecessor[v] := u
// Step 3: check for negative-weight cycles
for each edge (u, v) in Graph with weight w in edges:
if distance[u] + w < distance[v]:
error "Graph contains a negative-weight cycle"
return distance[], predecessor[]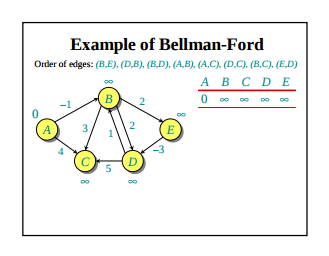
Problems you can attempt
1. UVa 558 - Wormholes (checking the existence of negative cycle)
2. UVa 10557 - XYZZY
3. UVa 11280 - Flying to Fredericton (modified Bellman Ford’s)