Le produit scalaire
Un cours présenté par Antoine AUER et Vincent MONARD
Définition
Le produit scalaire est une opération algébrique s'appliquant aux vecteurs. Il permet de calculer un angle, une distance entre deux vecteurs.
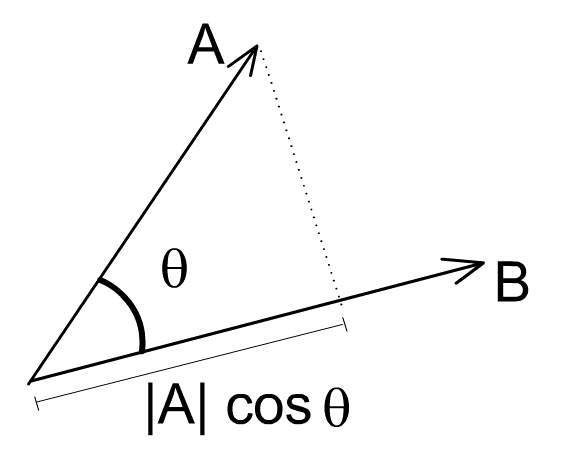
Étant donnés des points O, A et B, on considère les vecteurs OA et OB.
Lorsque ces vecteurs sont non nuls le produit scalaire est le nombre réel
OA.OB = OA x OB x cos(α)
où α représente une mesure de l'angle géométrique AÔB.
Propriétés
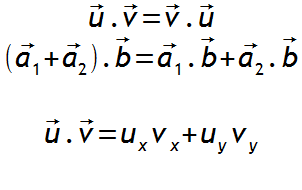
Norme d'un vecteur
Si A et B sont deux points du plan ou de l'espace usuel, la norme du vecteur AB est la distance AB c'est-à-dire la longueur du segment [AB].
On écrit :
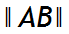
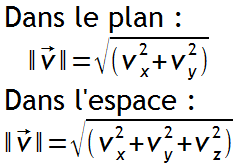
Vecteur unitaire
Un vecteur unitaire est un vecteur dont la norme est égale à 1.

Démonstration
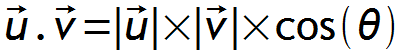
Utilisation
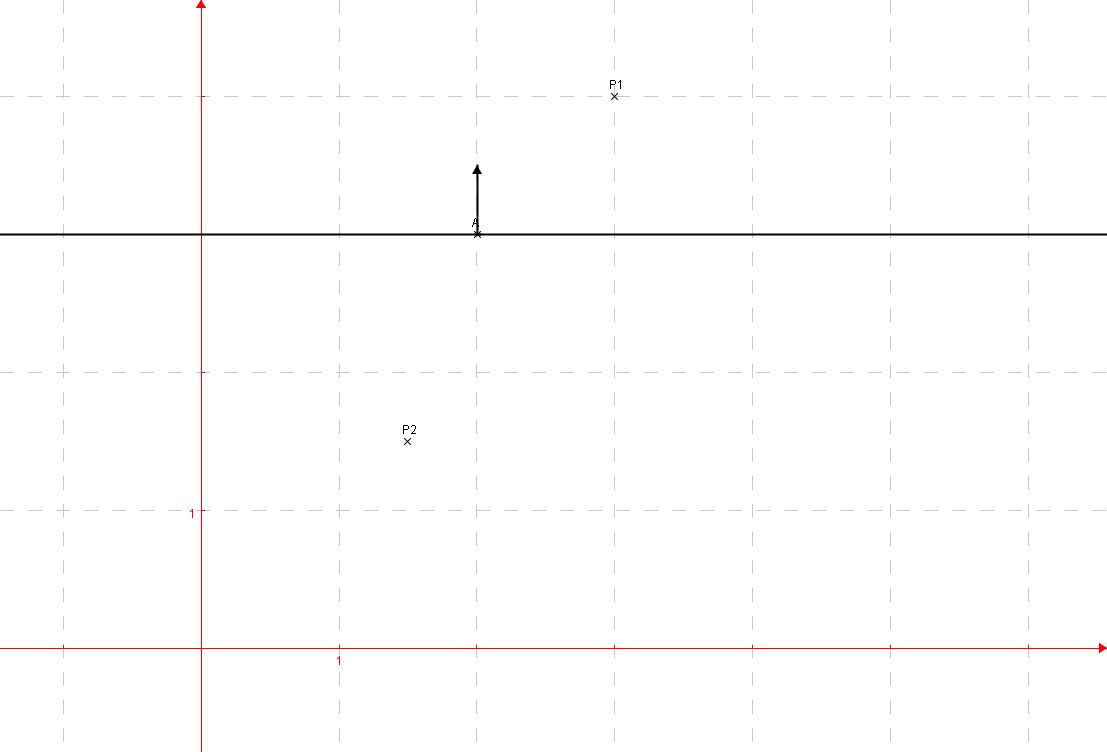
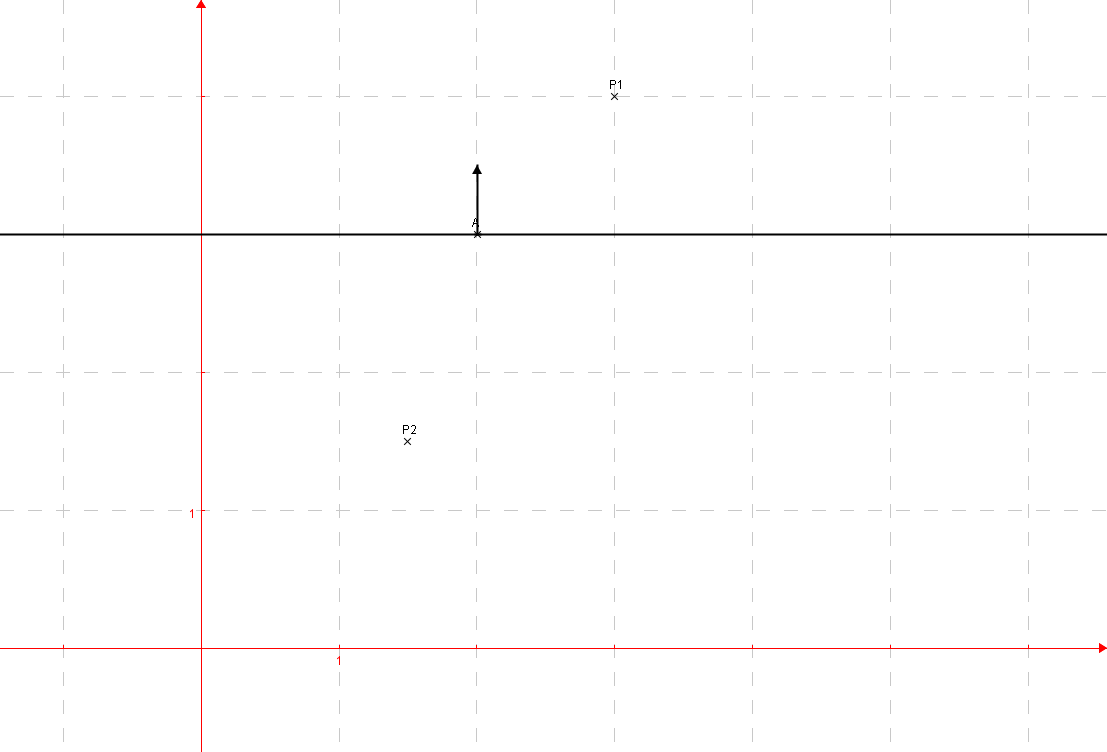
Comment prouver qu'un point P1 ou P2 est devant ou derrière une droite (d) ?
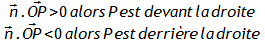
Utilisation
Est ce qu'un point P appartient à (d) ?


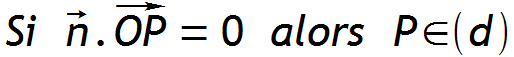
Utilisation
En connaissant les coordonnées du point P appartenant à (d), retrouver l'équation de (d) sous la forme : ax + bx + c = 0
Fin de la présentation
Franchement, c'était stylé !