R
E
A
C
T
O

xamples
epeat
ode
pproach
ptimize
est
{Rainwater Collector}

The Question
You're an industrious programmer that lives off the grid. The local well that you use to fetch water has gone dry, so you've decided to collect rain water to filter. However, your collection device isn't flat.
PROBLEM: Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water your collection device is able to trap after raining.

Example
EXAMPLE: Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

Keep in mind...
- Before we begin to sum the total water volume of the collector, it is important to use our understanding of water itself.
- Water will only gather upto the height of the reservoir walls
- We can therefore think about this problem in terms of height.
- Water cannot be held in the first or last bar, due to no containing wall on one side.

The Approach
-
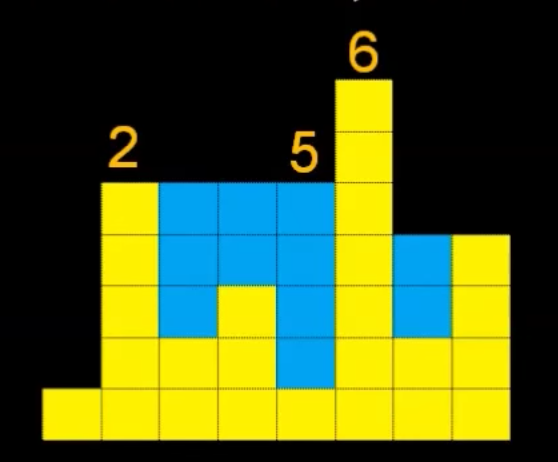
For each bar we aim to figure out how much rainwater exists above it. Look at the diagram below:
-
For rainwater to be on a bar, the height of bar should be less than (one of the bars on its left && one of the bars on its right) - i.e. trapped by the reservoir walls
-
Look at bar 2, there is no bar on the left that is taller than it, therefore it does not have any water on top of it.
-

Continued
-
Lets look at bar 5. We know that that 4 units of water exist above it. How did we get here?
-
If we look closely, we arrived at the solution by first looking on the left of Bar 5 and finding the max height on the left side which is Bar 2, and then looking on the right of Bar 5 and finding the max height which is Bar 6. Finally the minimum(Bar 2 , Bar 6) - Bar 5 gave our solution which is 4 unit of water.
-
-
Algorithm:
1: With given towerHeight array, create 2 arrays, leftMax and rightMax.
leftMax[i] - max height on left side of heights[i].
rightMax[i] - max height on right side of heights[i].
2: Calculate for each tower:
rainwater = rainwater + Max(Min(leftMax[i], rightMax[i]) - heights[i], 0);
// we cannot have (negative height)
// e.g. heights: 0 3 2 1 5 1
// leftMax: 0 0 3 3 3 5
// rightMax: 5 5 5 5 1 0
// leftMax[0] and rightMax[heights.length - 1] will be 0 (edges of the reservoir - so no max)
// what that means is?
// for index 1 -> height = 3
// 0 is its left max, 5 is its right max
// that gives zero volumn as it cannot hold water (draw it out)
// for index 2 -> height 2
// 3 is its left max and 5 is its right max -> min(3,5) = 3
// and height 2 is the bottom of the water bed
// so that gives (3-2) -> 1 volumn of watervar rainWaterCollector = function(height) {
var leftMax = [0];
var rightMax= [];
rightMax[height.length - 1] = 0
var water = 0;
// to get the left of i so we do i - 1
for(var i = 1; i < height.length; i++) {
leftMax[i] = Math.max(leftMax[i - 1], height[i - 1]);
}
for(i = height.length - 2; i >= 0; i--) {
rightMax[i] = Math.max(rightMax[i + 1], height[i + 1]);
var minHeight = Math.min(leftMax[i], rightMax[i]);
var waterBottom = height[i];
if(minHeight > waterBottom) {
water += (minHeight - waterBottom);
}
}
return water;
};
Tests to Run
// vol = 7
var a = [0,0,1,2,4,3,2,5,0,0,2,1]
console.log('collection device "a" can hold', rainWaterCollector(a))
// vol = 6
var b = [0,1,0,2,1,0,1,3,2,1,2,1]
console.log('collection device "b" can hold', rainWaterCollector(b))
// vol = 12
var c =[0,3,0,1,0,0,0,1,0,2]
console.log('collection device "c" can hold', rainWaterCollector(c))
// vol = 8
var d = [0,1,0,3,5,0,0,0,2,0,1]
console.log('collection device "d" can hold', rainWaterCollector(d))
// vol = 38
var e = [0,5,3,2,8,8,1,1,2,4,3,3,7,1,2,4,3,2]
console.log('collection device "e" can hold', rainWaterCollector(e))
Alternate O(n*a)
-
Instead of summing the volume vertically, we can think about how much volume exists in a horizontal plane at each incremental height.
-
The solution goes about this by
-
starting at the highest 'peak',
-
summing the total amount of volume at that level,
-
decrementing the height by 1 and
-
repeating the process until a height of 0 is reached.
-