Теория пределов
11 класс
vkrysanov320@gmail.com
version 0.1, 25-10-2020
Новая идея математического анализа
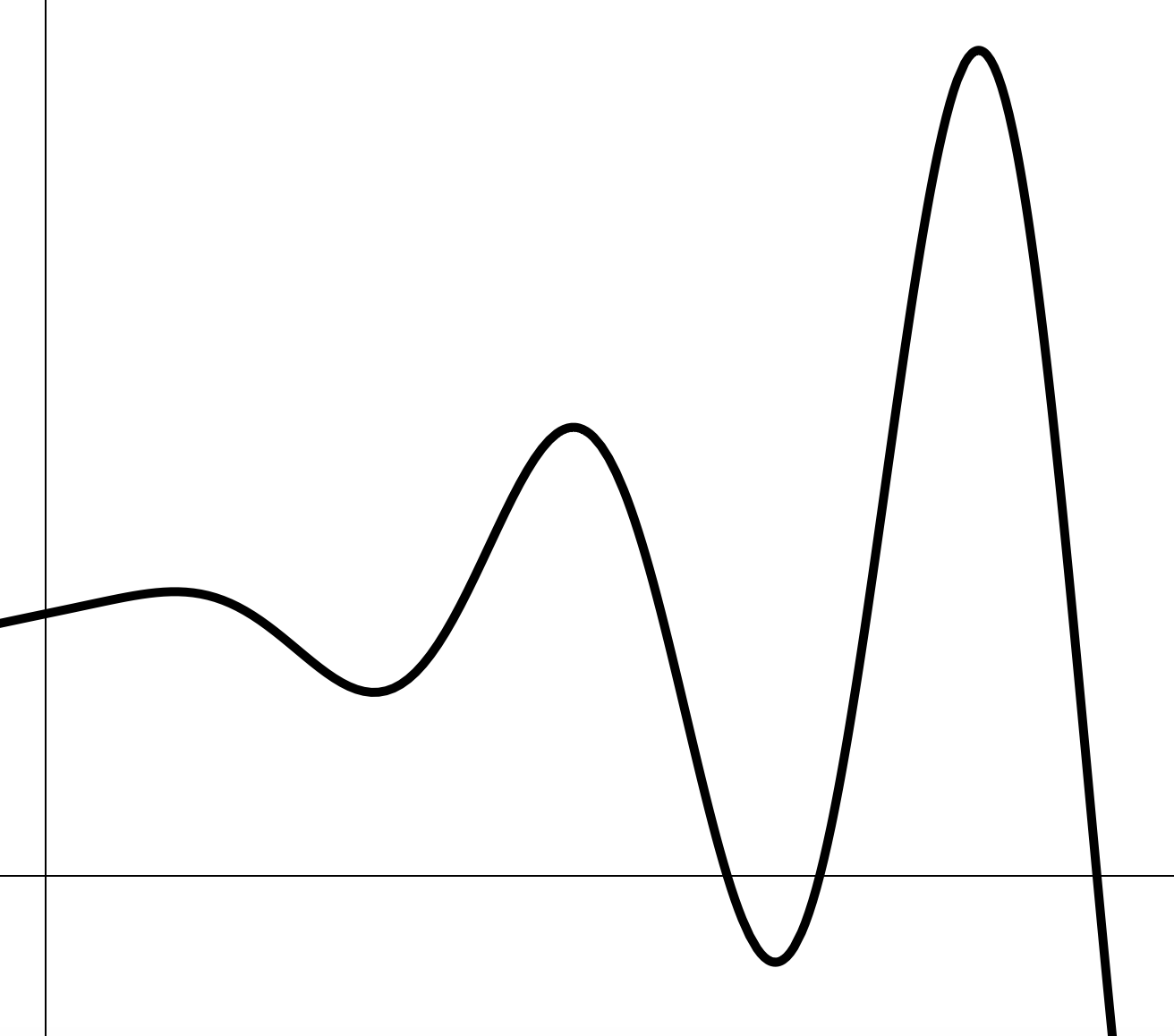

Нам понятно, что делает функция в точке , но как она выглядит если подойти очень- очень близко к точке ?
Новая идея математического анализа (2)
Рассмотрим функцию . Она определена для всех , кроме .
Рассмотрим, как изменяются значения этой функции при неограниченном возрастании :
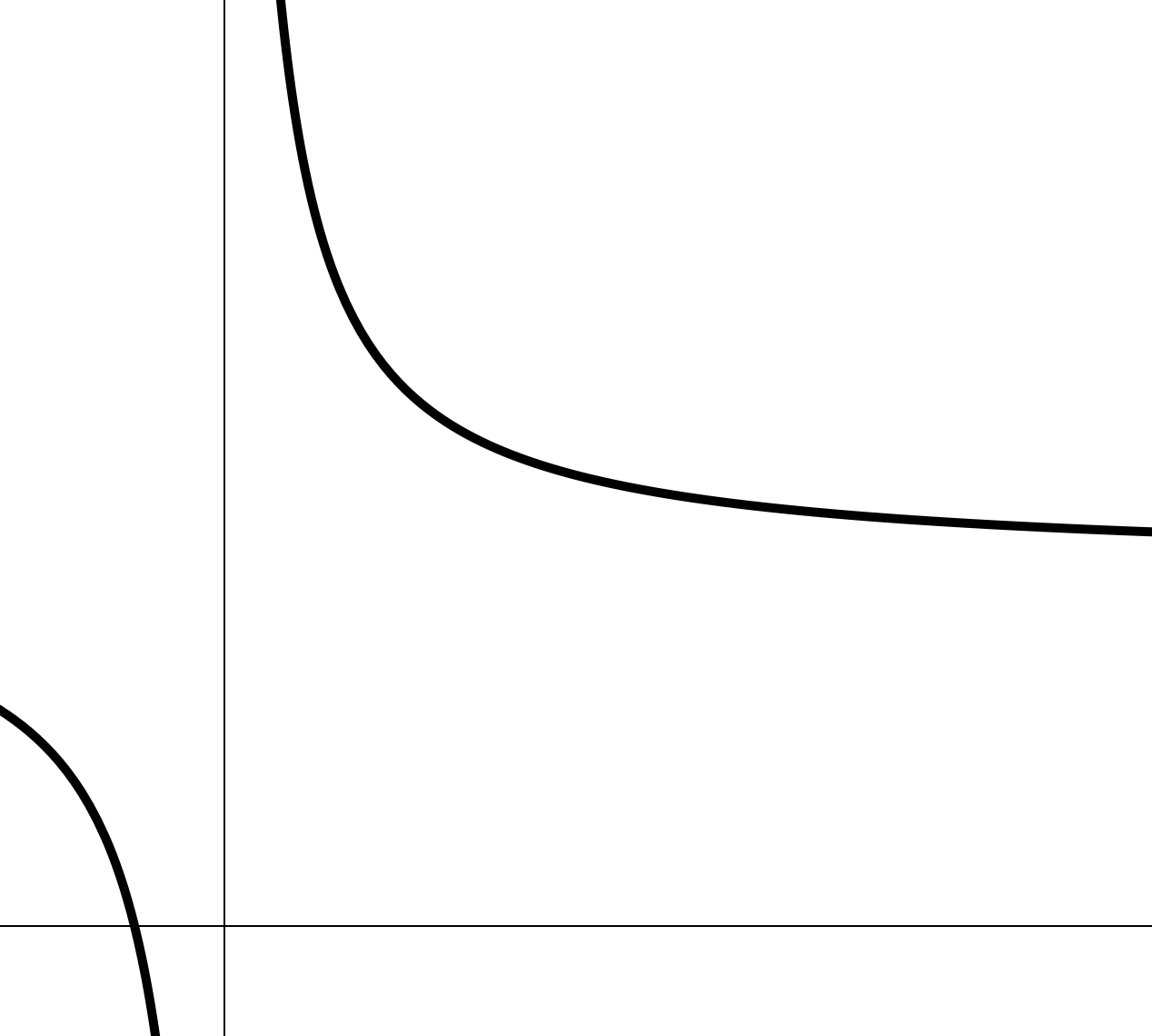
Значения данной функции приближаются к двум, когда независимая переменная неограниченно возрастает.
Данное в математике записывается следующим образом: .
Новая идея математического анализа (3)
А теперь рассмотрим, как изменяются значения этой функции при приближении зависимой переменной к единице:

Значения данной функции приближаются к трем, когда независимая переменная стремится к одному.
приближение слева:
приближение справа:
Данное в математике записывается следующим образом: .
Ещё пример
Несмотря на то, что функция не существует в точке ,
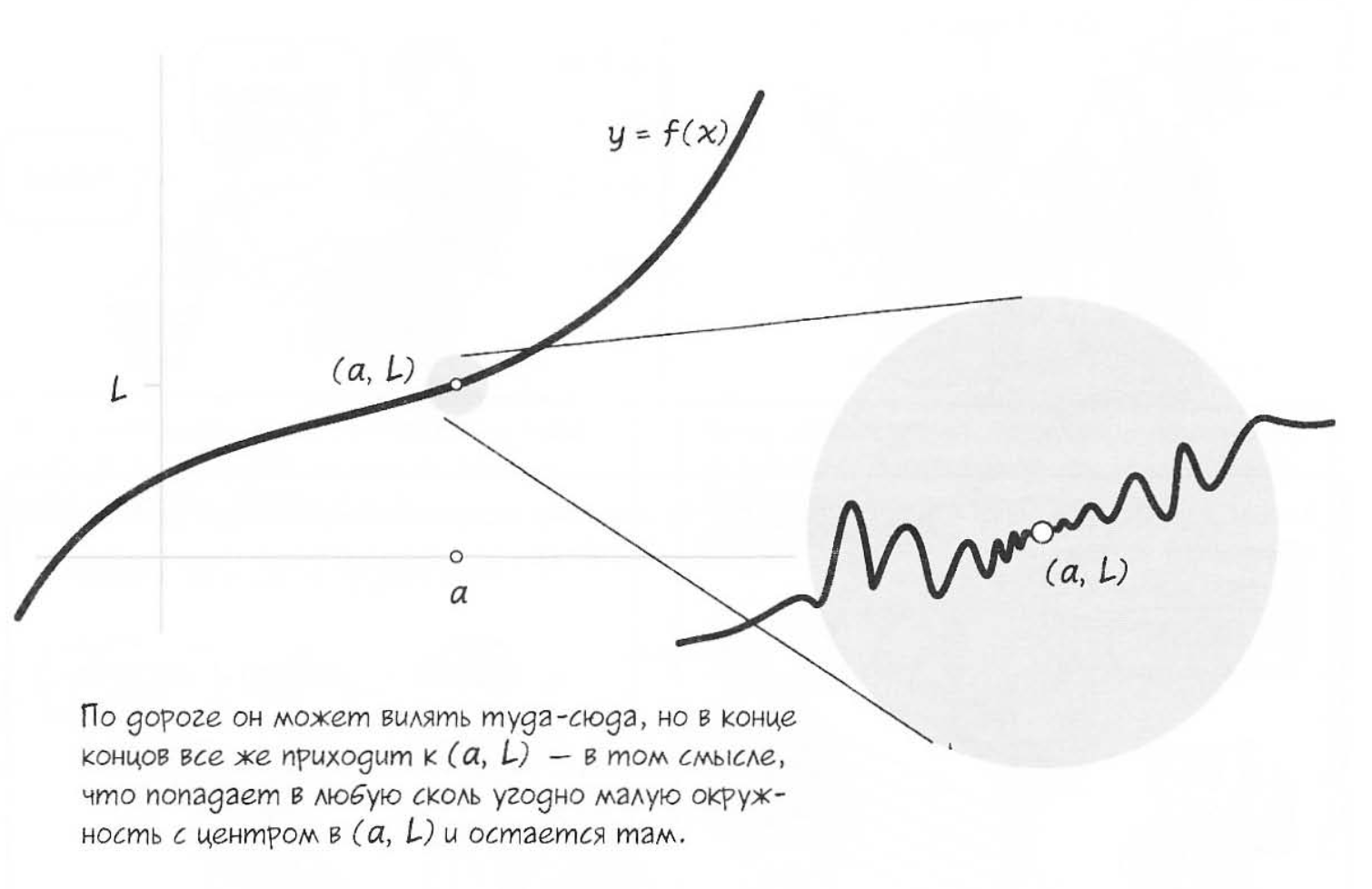
По дороге график может вилять туда-сюда, но в конце концов все же приходит к — в том смысле, что попадает в любую сколь угодно малую окружность с центром в и остается там.
Запись
оператор предела
аргумент предела
значение предела
или:

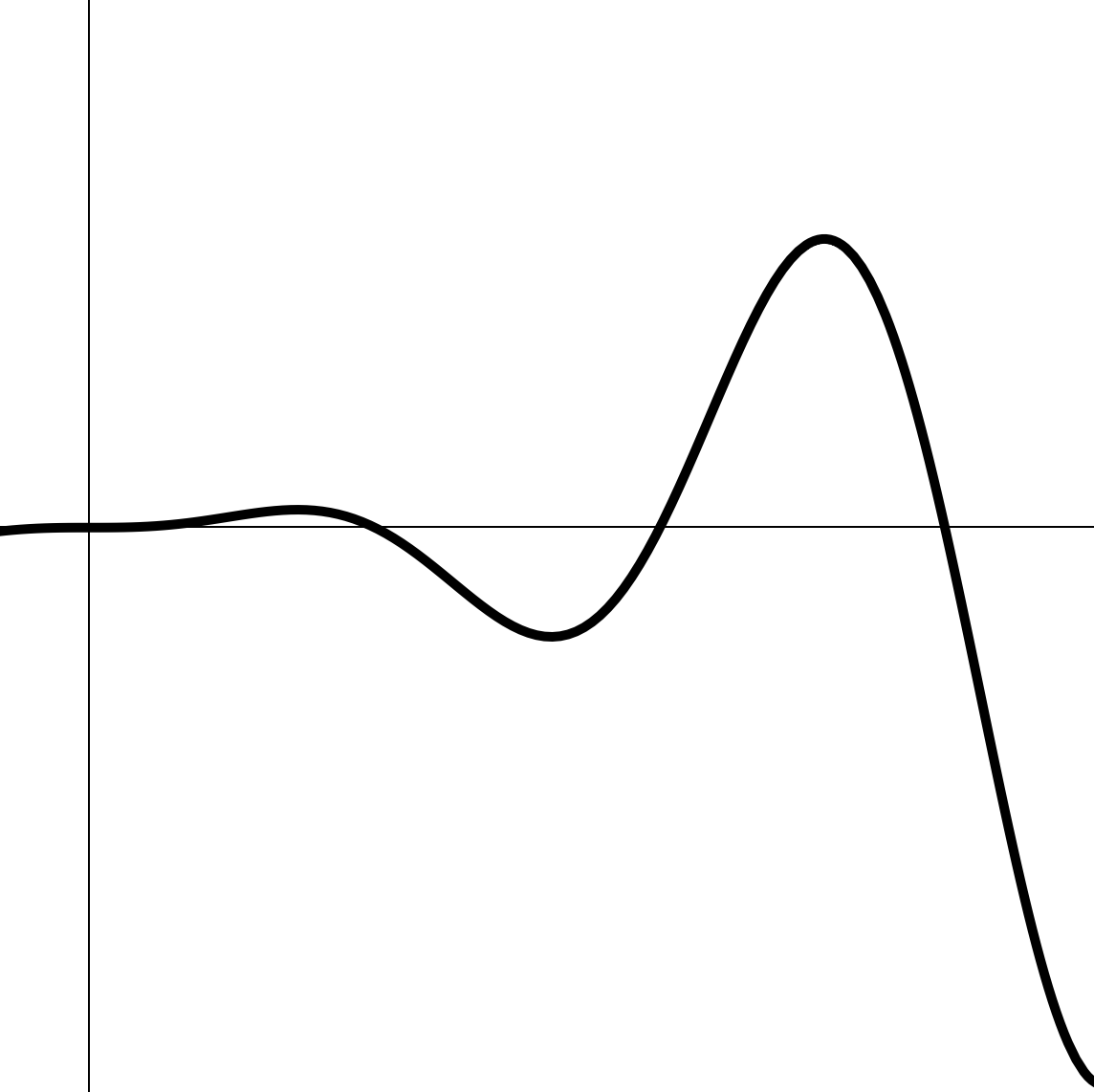
Предел функции при
Примеры:
1)
2)
3)
4)
Почти всегда, но не всегда...
Предел функции при
Число является пределом функции при , если каково бы ни было , можно найти числа и , что для всех , лежащих в интервале
(за исключением быть может точки ) выполняется неравенство
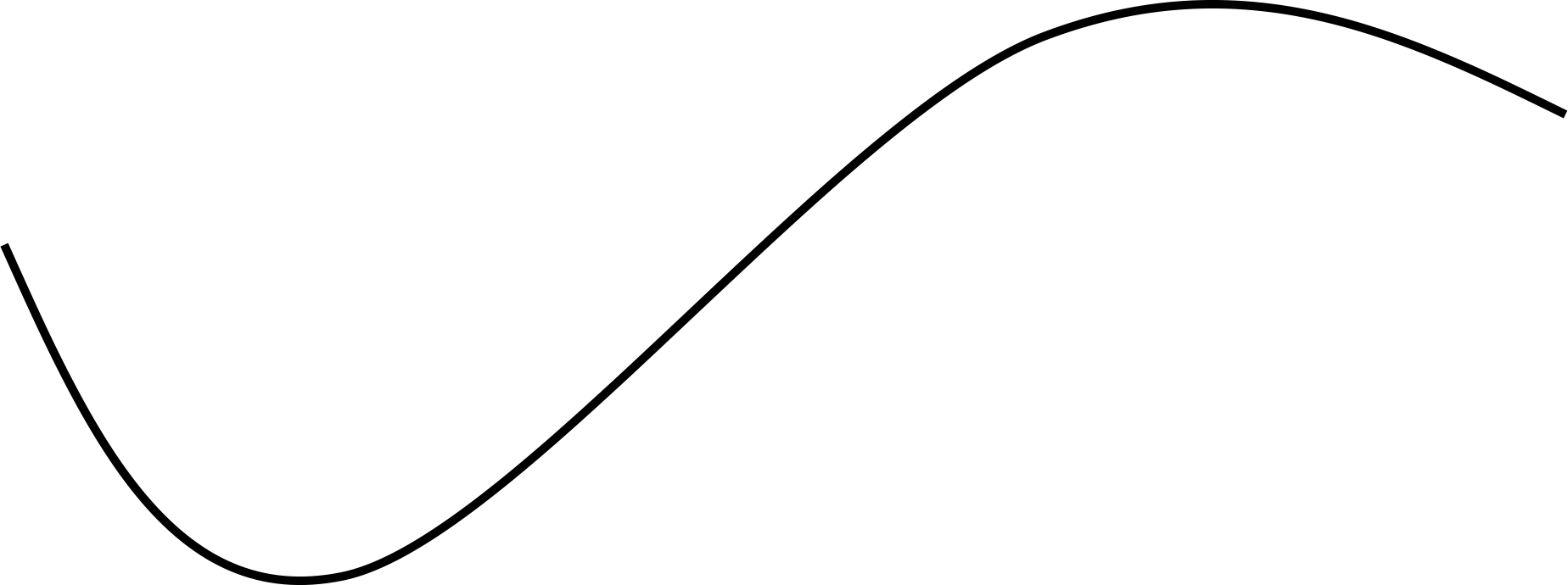
Примеры:
1)
2)
3)
4)
Предел функции при
Число является пределом функции при , если каково бы ни было положительное число , можно найти число , что для всех выполняется неравенство
Примеры:
1)
2)
3)
4)

Предел функции при
Число является пределом функции при , если каково бы ни было положительное число , можно найти число , что для всех выполняется неравенство
Примеры:
1)
2)
3)
4)

А есть ли разница, с какой стороны приближаться?
Конечно есть! И опять эта функция ...
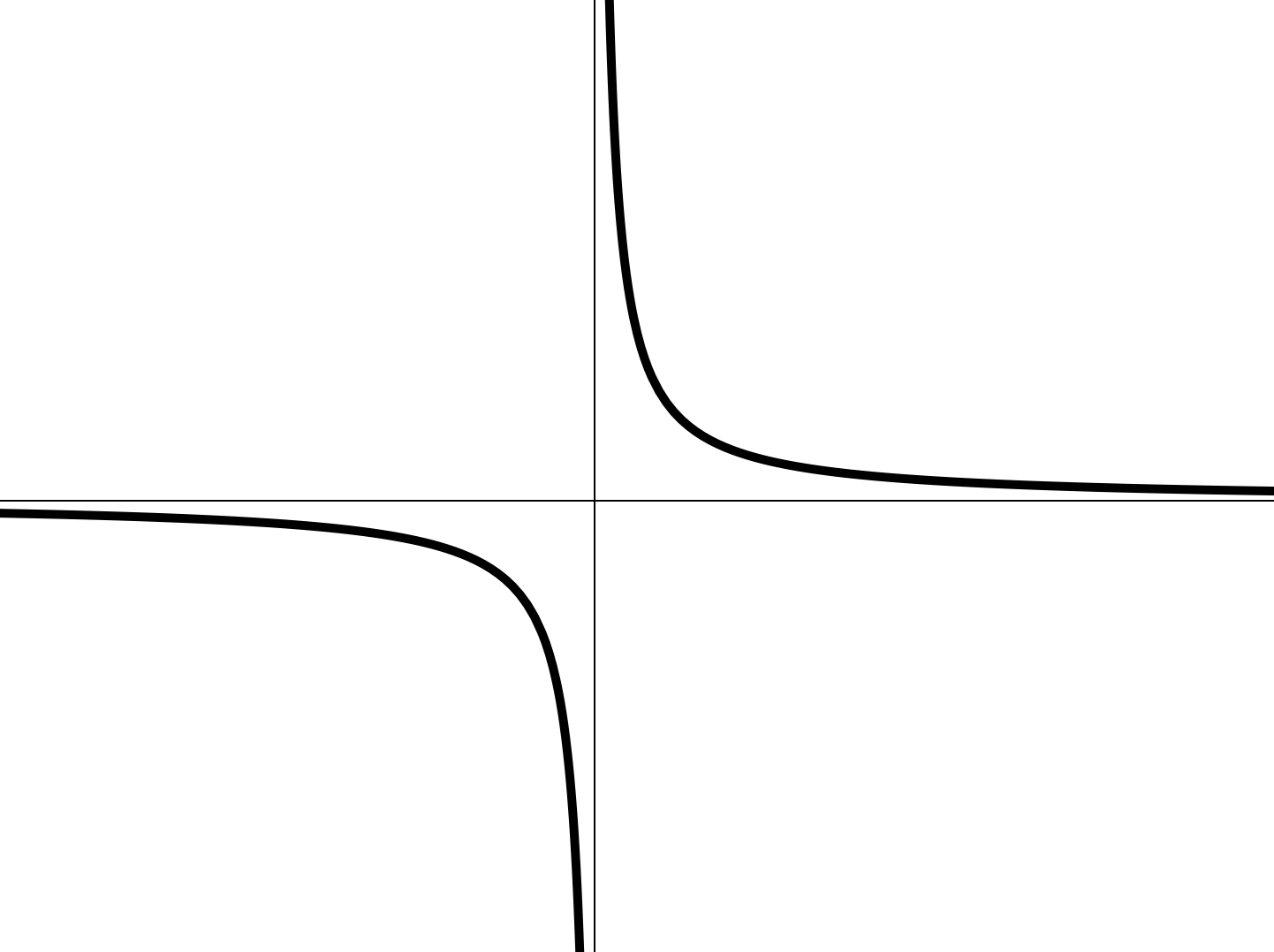
приближение слева:
*стремится к
Левосторонний предел
приближение справа:
*стремится к
Правосторонний предел
Односторонние пределы
Левосторонний, правосторонний и двусторонний предел
Если оба односторонних предела существуют и равны между собой, то говорят, что функция имеет двусторонний предел при или просто имеет предел при

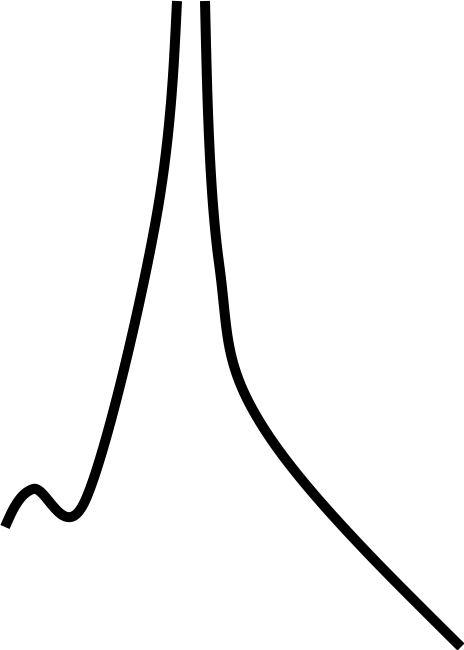

Пример I
Пример II
Пример III
Разные понятия!
Разрыв
Разрыв
Разрыв
Точки разрыва
У точек разрыва имеется определенная классификация, на ней мы останавливаться не будем.
Но, если есть подозрения на разрыв функции в точке, то для определения и вычисления двустороннего предела необходимо вычислить односторонние!
Пример 1
- Левосторонний:
- Правосторонний:
Найти , если
односторонние пределы равны
а значит, существует и двусторонний
точка разрыва
Ответ:
Пример 2
- Левосторонний:
- Правосторонний:
Найти , если
односторонние пределы неравны
а значит, двусторонний предел не существует!
точка разрыва
Ответ: не существует.
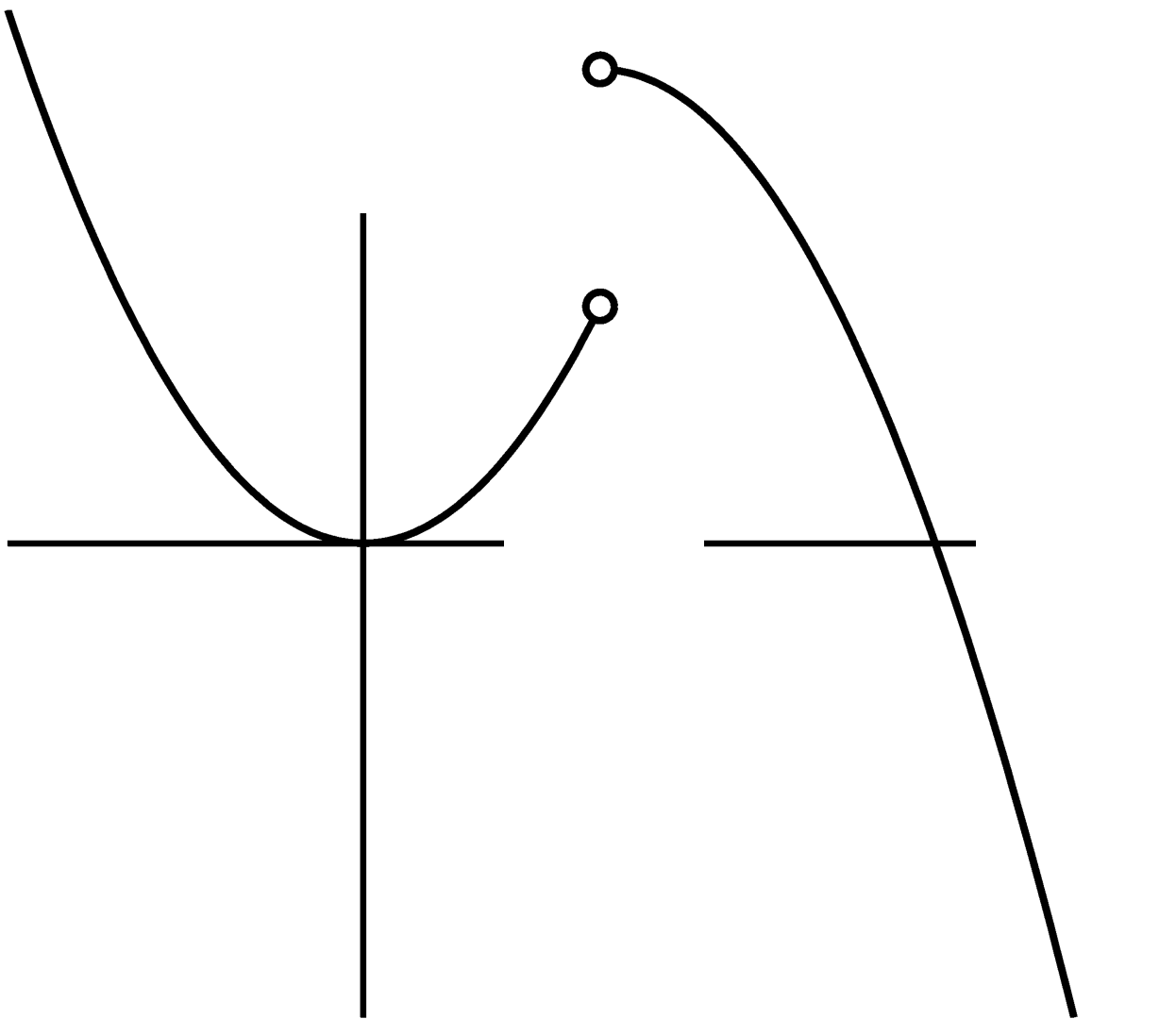
Условие непрерывности функции в точке
Определение: функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке:
Если более детально, то:
1. Функция должна быть определена в точке , то есть должно существовать значение .
2. Должен существовать общий предел функции: А то есть существование и равенство односторонних пределов:
3. Предел функции в данной точке должен быть равен значению функции в этой точке:
*Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке .
Элементарный пример
Определить наличие точки разрыва при :
Решение:
1) Проверяем существование функции при :
2) Проверяем существование двустороннего предела:
3) Сравниваем значение предела при и значение функции в этой же точке:
равны, следовательно функция является непрерывной при
(п. 2)
(п. 1)
Задачи
1. Вычислить пределы функций:
2. Вычислить односторонние пределы и двусторонние пределы (если определены):
а)
б)
в)
г)
д)
е)
ж)
з)
и)
а) б)
Вычисление пределов
Свойства пределов
Теорема 3 (св-во суммы):
Теорема 4 (св-во произведения):
- Следствие 1 (св-во постоянного множителя):
- Следствие 2 (св-во целой положит. степени):
Теорема 5 (св-во частного):
где
Теорема 2 (св-во постоянной):
Теорема 1:
Одна и та же функция в одной и той же точке может иметь только один
предел.
Неопределенности
Часто при подстановке предельного значения в функцию получаются выражения следующих видов:
Эти выражения называются неопределенностями, а вычисление пределов в этом случае называется раскрытие неопределенности.
Неопределенность вида
Если предел вида (где и — многочлены) при подстановке
предельного значения обращается в неопределенность вида , то следует
разложить числитель и знаменатель на множители, сократить общие множители и подставить предельное значение вновь.
Пример: вычислить
Решение:
Неопределенность вида (2)
Пример: вычислить
Решение:
Если предел вида или (где —
многочлены) при подстановке предельного значения обращается в
неопределенность вида , то следует числитель и знаменатель дроби умножить на сопряженное выражение , затем упростить и подставить предельное значение вновь.
Неопределенность вида
Пример 1: вычислить
Решение:
Пример 2: вычислить
Решение:
Если предел вида при подстановке предельного
значения обращается в неопределенность вида , необходимо числитель и знаменатель дроби разделить почленно на , где , затем упростить и подставить предельное значение вновь.
Неопределенность вида
Неопределённость вида устраняется двумя распространёнными способами: приведением выражения под знаком предела к общему знаменателю и умножением/делением на сопряжённое выражение.
Пример: вычислить
Решение:
Неопределенности другого вида сводятся к замечательным пределам (об этом позже) или же применяются другие методы, которые мы рассматривать не будем...
Задачи
а)
б)
в)
г)
д)
ж)
з)
и)
й)
к)
л)
м)
Первый замечательный предел
Рассмотрим функцию
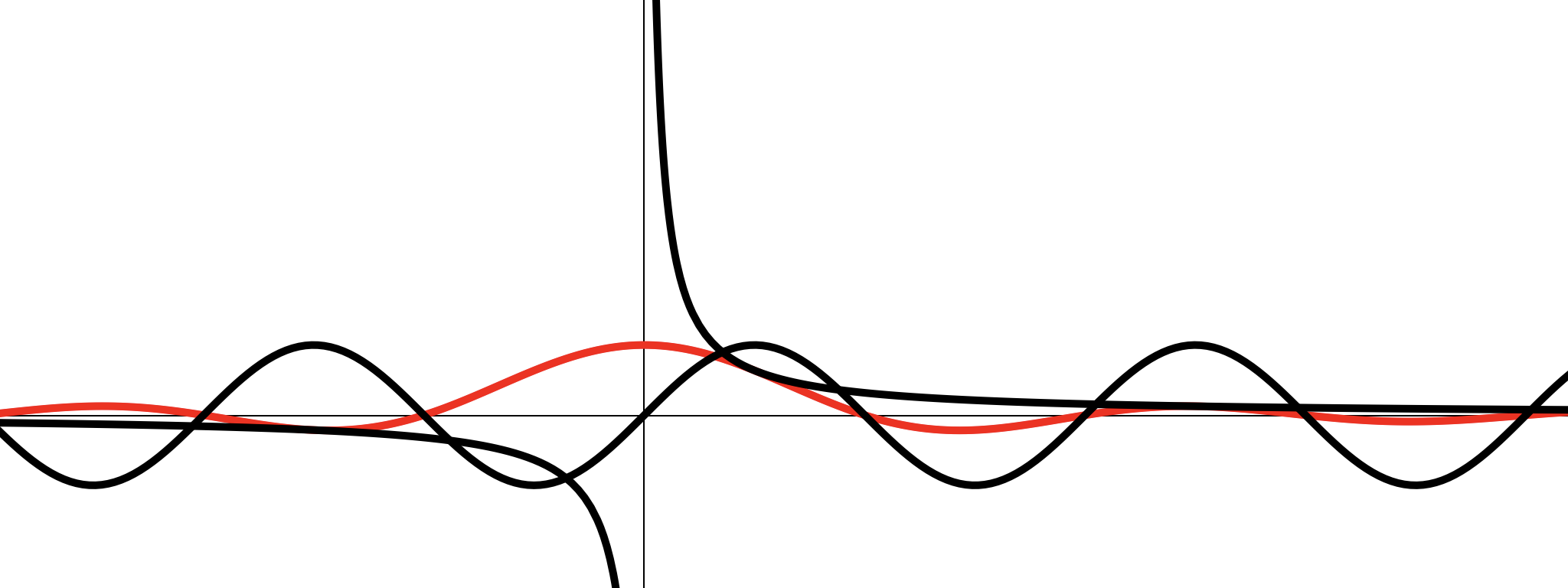
Точка разрыва
Примеры
Пример 1: вычислить
Решение:
Пример 2: вычислить
Решение:
Пример 3: вычислить
Решение:
Но тут ошибочка... Почему?
Задачи
а)
б)
в)
г)
д)
ж)
з)
и)
й)
к)
л)
м)
Второй замечательный предел
Рассмотрим функцию
Точка разрыва при . Но при сближении что слева, что справа к нулю: , .