Тетраэдр, параллелепипед. Сечения многогранников
10 класс
vkrysanov320@gmail.com
Как при помощи шести спичек сложить четыре одинаковых треугольника?
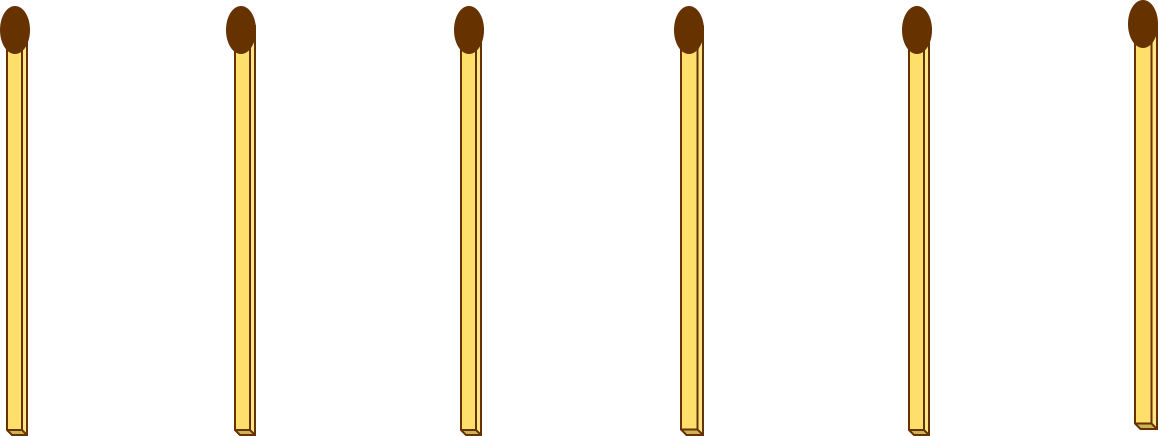
...и что это за фигура?

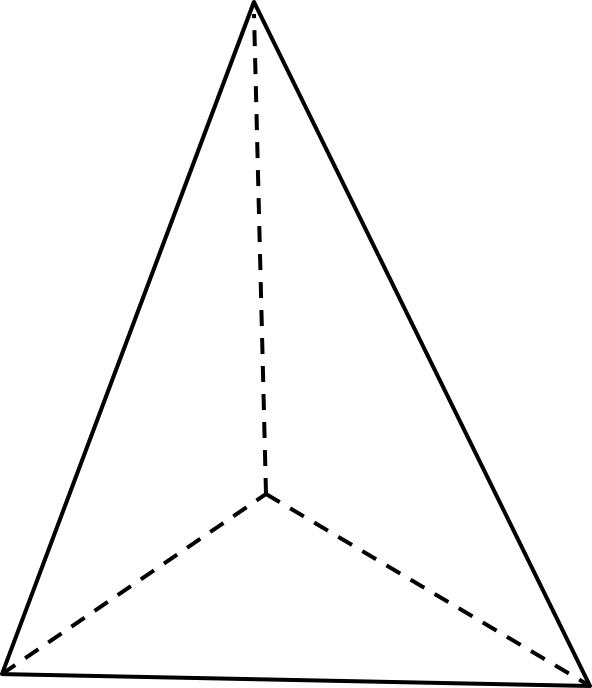
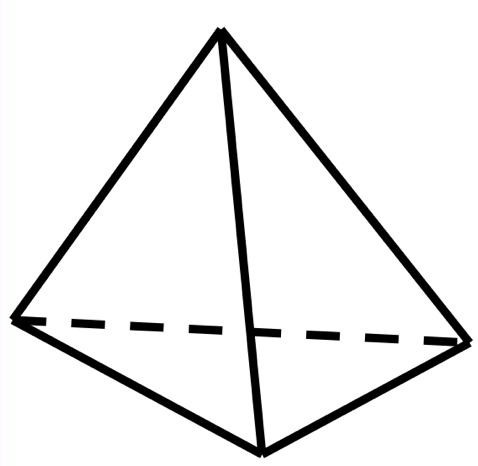
Тетраэдр
Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греч. tetra — четыре и hedra — грань)
— грани тетраэдра
— тетраэдр
— вершины тетраэдра
Площадь боковой пов-ти тетраэдра
Площадью полной поверхности тетраэдра называется сумма площадей всех его граней:
Площадью боковой поверхности тетраэдра
называется сумма площадей его боковых граней:
Объединение боковых граней называется
боковой поверхностью тетраэдра.
Объединение всех граней называется
полной поверхностью тетраэдра.

основание
где
и с тетраэдром пока все ...
Параллелепипед
Параллелепипед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них — параллелограмм.
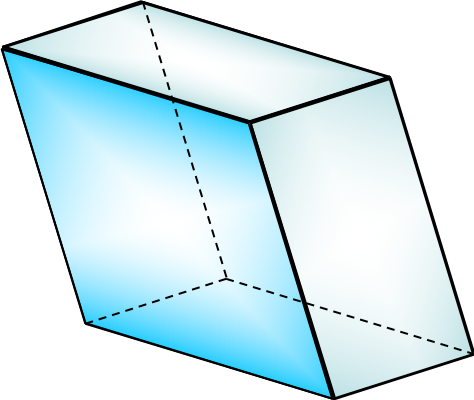
— вершины параллелепипеда
— параллелепипед
Параллелепипед (2)
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.


у параллелепипеда всего 4 диагонали
Виды параллелепипедов
наклонные
прямоугольные

Боковые грани расположены по отношению к основаниям под углом, не равным 90°.
Все боковые грани — прямоугольники,
основания — прямоугольники.
Свойства параллелепипеда
1. Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.









2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Площадь боковой пов-ти параллелепипеда
Площадью полной поверхности параллелепипеда называется сумма площадей всех его граней:



Площадью боковой поверхности параллелепипеда
называется сумма площадей его боковых граней:
Объединение боковых граней называется
боковой поверхностью параллелепипеда.
Объединение всех граней называется
полной поверхностью параллелепипеда.
где
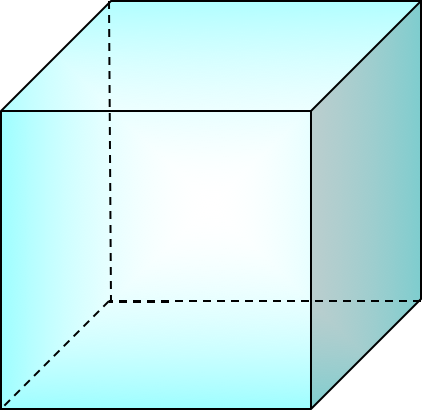
Куб
Куб — это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани которого — равные квадраты.
Диагональ куба со стороной равна:
Задачи
1. Дан прямоугольный параллелепипед, стороны основания которого равны 4 и 5, а боковое ребро равно 3. Найдите наибольшую площадь его грани.
2. Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185, 37 и 37. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
3. Дан прямоугольный параллелепипед с ребрами 2, 3 и 6. Найдите его диагональ.
4. В прямоугольном параллелепипеде диагональ грани равна 5 , а
Найдите диагональ параллелепипеда.
Задачи (2)
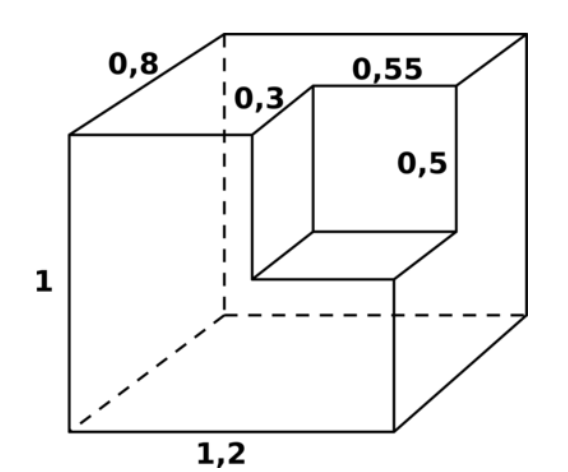
5. Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
6. В тетраэдре дано:
Найти ребра основания данного тетраэдра; площади всех боковых граней.
7. В основании прямого параллелепипеда лежит параллелограмм с основаниями 4 см и 6 см и острым углом 30°. Боковое ребро параллелепипеда равно 5 см. Найти площадь полной поверхности параллелепипеда.
Задачи (3)
8. Две стороны основания параллелепипеда равны 5 см и 4 см, угол между ними 30°. Боковое ребро равно 6 см и наклонено к основанию под углом 60°. Найти объём параллелепипеда.
9. Все грани параллелепипеда — ромбы с диагоналями 6 см и 8 см. Найдите площадь полной поверхности параллелепипеда.
10. В правильной треугольной пирамиде SABC P — середина ребра AB, S — вершина. Известно, что BC = 5, а SP = 6. Найдите площадь боковой поверхности пирамиды.
11. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Сечения, что это?
Плоскость, которая пересекает многогранник, называется секущей.
Секущая плоскость пересекает грани многогранника по отрезкам, в результате получается многоугольник, который и называется сечением.
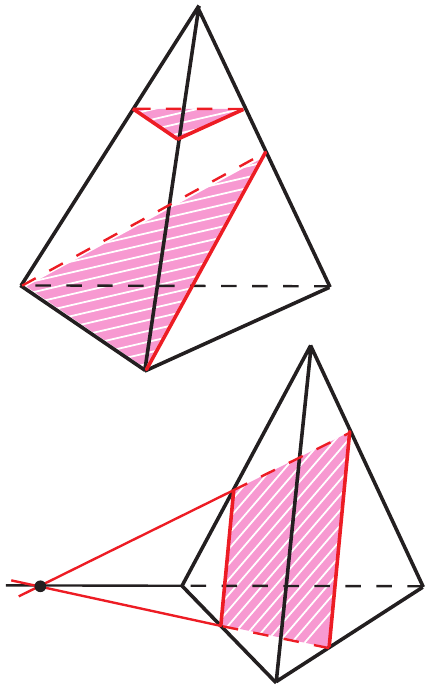
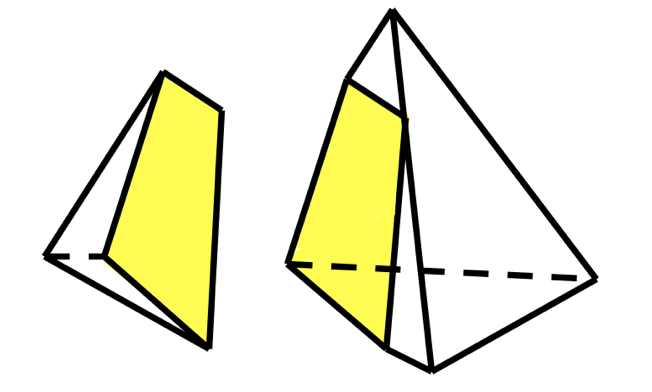
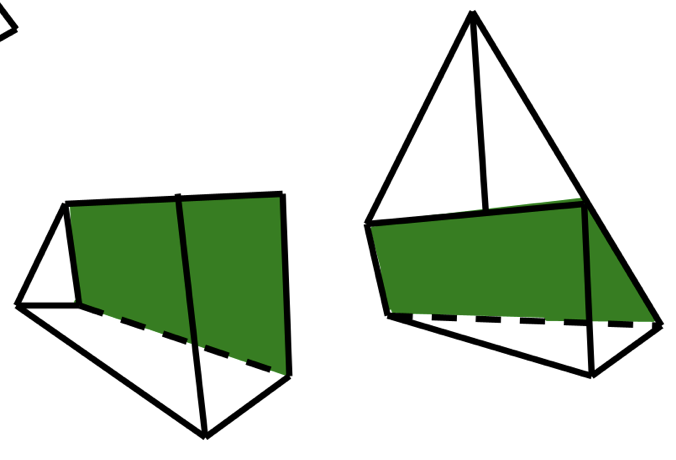
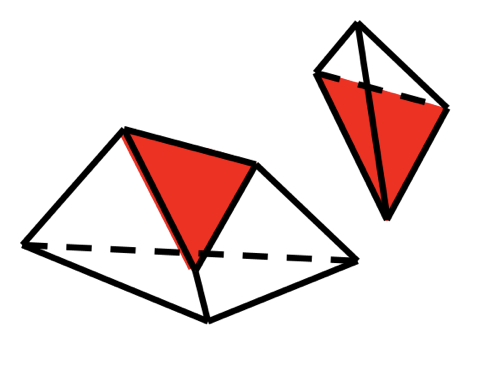
«Разрежем» тетраэдр на какие-либо части
Сечения, что это? (2)
С точки зрения геометрии, можно представить «разрезание»многогранника, как пересечение его плоскостью.
Линии, по которым эта плоскость пересечет грани, будут сторонами многоугольника, который получится в сечении.
Правила построения сечений
I) проводим прямые через точки, лежащие в одной плоскости;
II) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:
- ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
- параллельные грани плоскость сечения пересекает по параллельным прямым.
Пример I
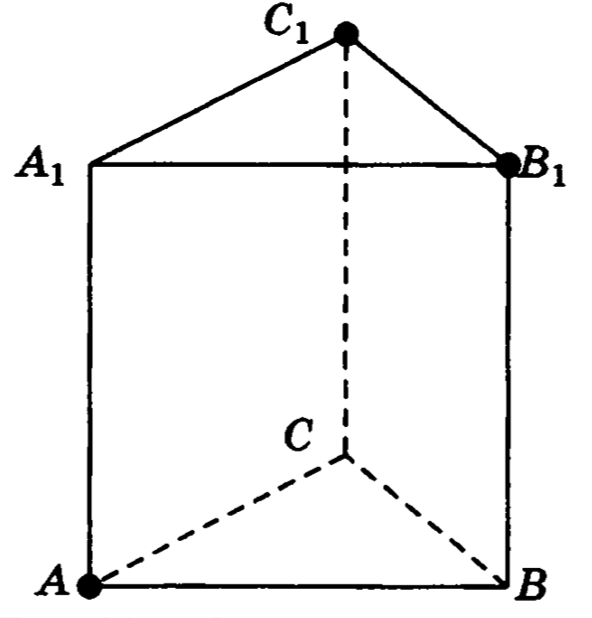

т.к. и лежат в одной плоскости

т.к. и лежат в одной плоскости
искомое сечение —
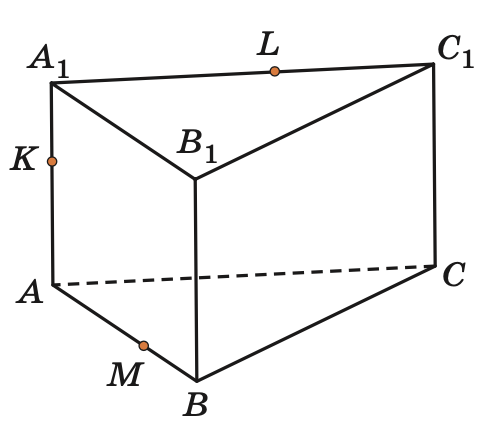
Построить сечение треугольной призмы , проходящее через точки

аналогично
*Последовательность построения вершин и сторон сечения не существенна (но с учетом всех аксиом и теорем)!

Пример II
искомое сечение —
Построить сечение треугольной призмы , проходящее через точки

т.к. и лежат в одной плоскости

аналогично 1)


аналогично 1)

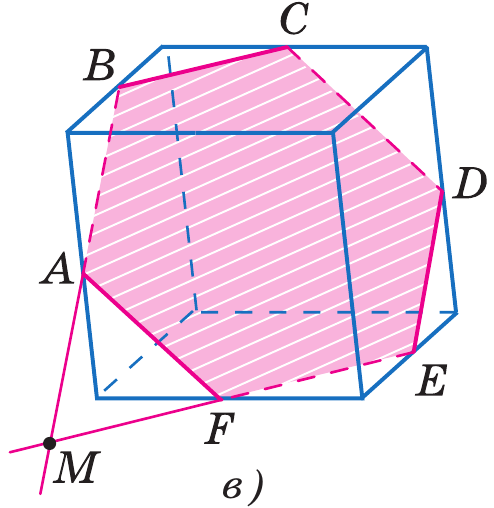
метод следов
Задачи
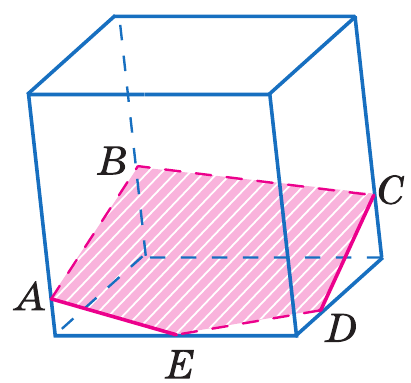
1. Построить сечение прямоугольного параллелепипеда , проходящее через вершины
2. Построить сечение прямоугольного параллелепипеда , проходящее через вершины и середины ребер и
3. Построить сечение прямоугольного параллелепипеда , проходящее через середины ребер



Задачи (2)
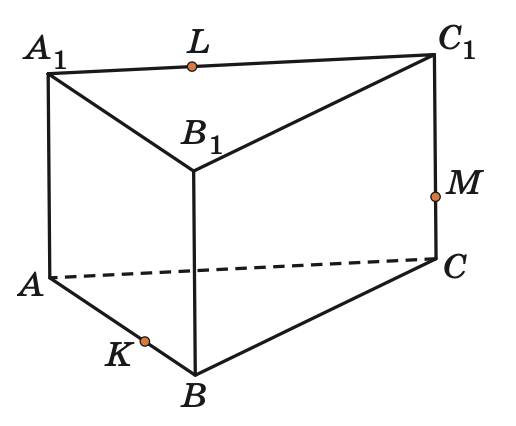
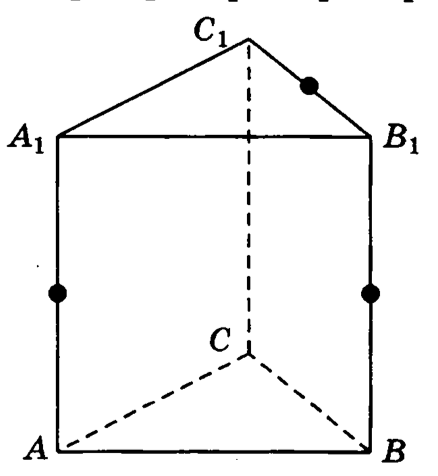
4. Построить сечение прямой треугольной призмы , проходящее через отмеченные жирным точки:

a) b) c) d)
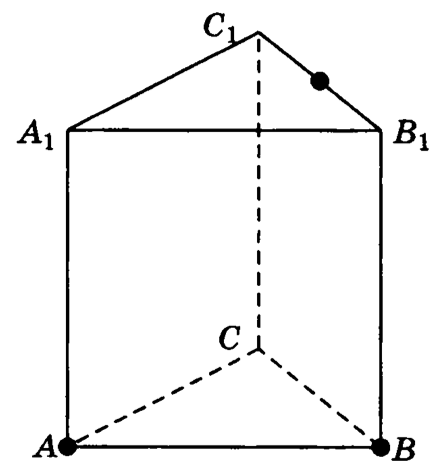
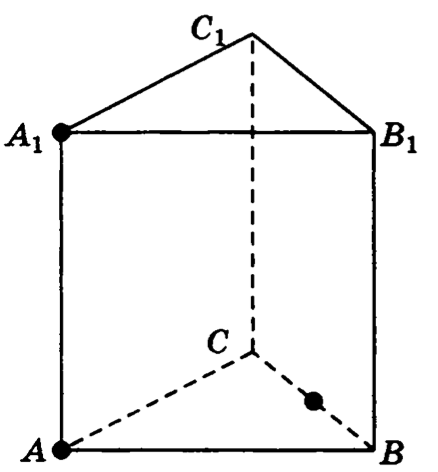
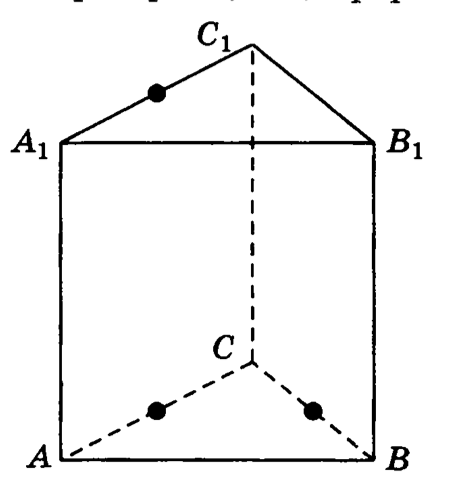
Задачи (3)
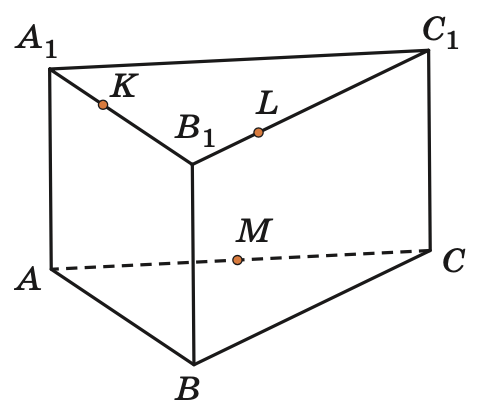
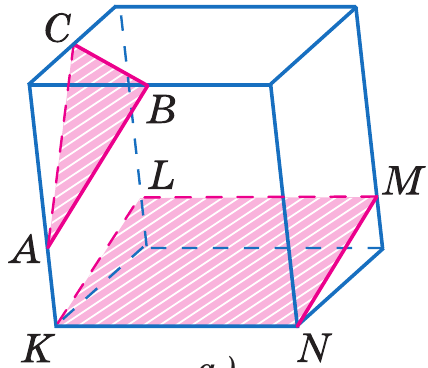
5. Построить сечение параллелепипеда , проходящее через отмеченные жирным точки:

a) b) c) d)
Задачи (3)
5. Построить сечение параллелепипеда , проходящее через отмеченные жирным точки:
a) b) c)