Интегральное исчисление
11 класс
vkrysanov320@gmail.com
Новая идея математического анализа
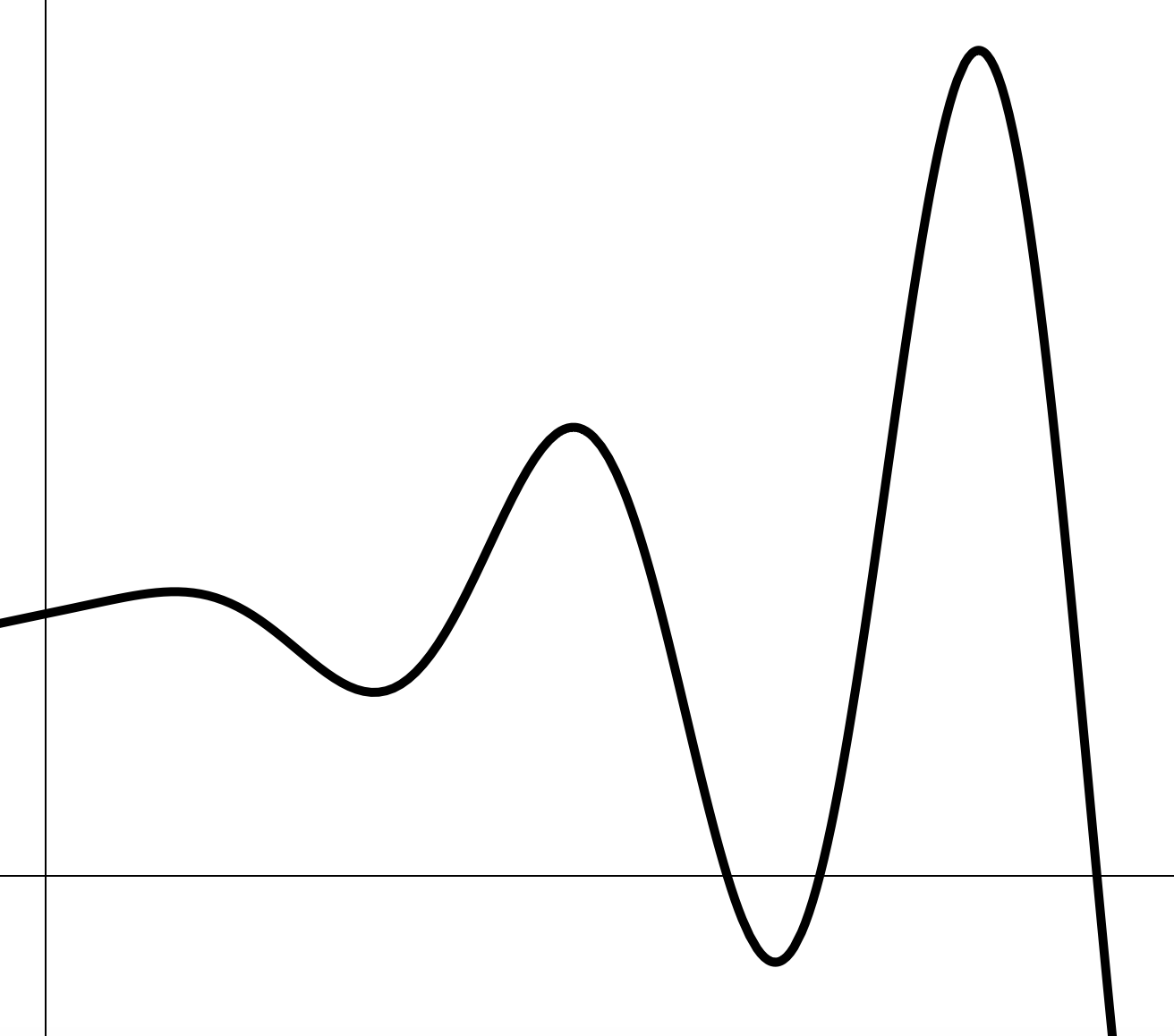

Нам понятно, что делает функция в точке , но как она выглядит в, если подойти очень- очень близко к точке ?
Новая идея математического анализа (2)
Рассмотрим функцию . Она определена для всех , кроме .
Рассмотрим, как изменяются значения этой функции при неограниченном возрастании :
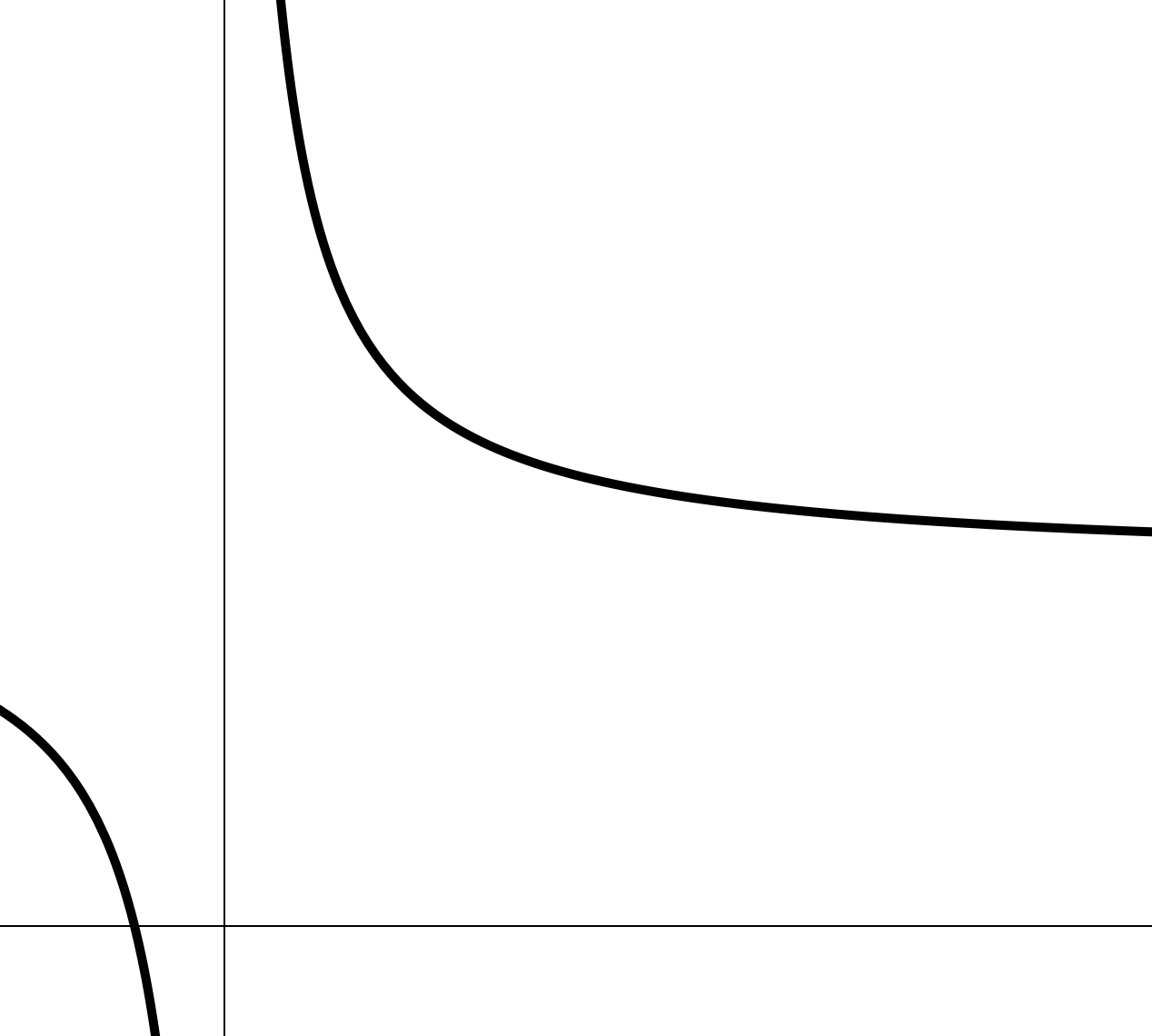
Значения данной функции приближаются к двум, когда независимая переменная неограниченно возрастает.
Данное в математике записывается следующим образом: .
Новая идея математического анализа (3)
А теперь рассмотрим, как изменяются значения этой функции при приближении зависимой переменной к единице:

Значения данной функции приближаются к трем, когда независимая переменная стремится к одному.
приближение слева:
приближение справа:
Данное в математике записывается следующим образом: .
Еще пример
Несмотря на то, что функция не существует в точке ,
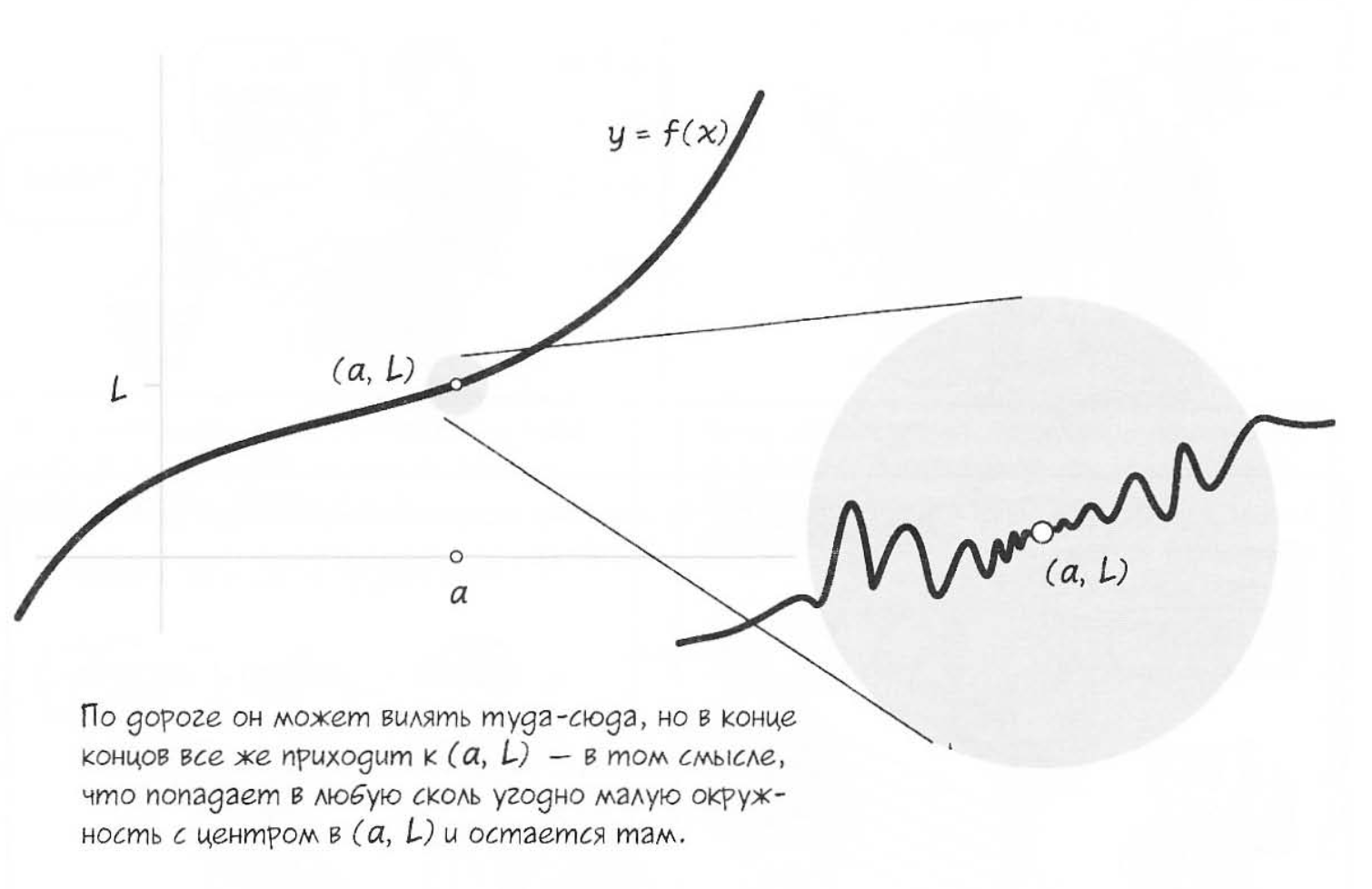
По дороге график может вилять туда-сюда, но в конце концов все же приходит к — в том смысле, что попадает в любую сколь угодно малую окружность с центром в и остается там.
Идея пределов при стремлении к конечной величине

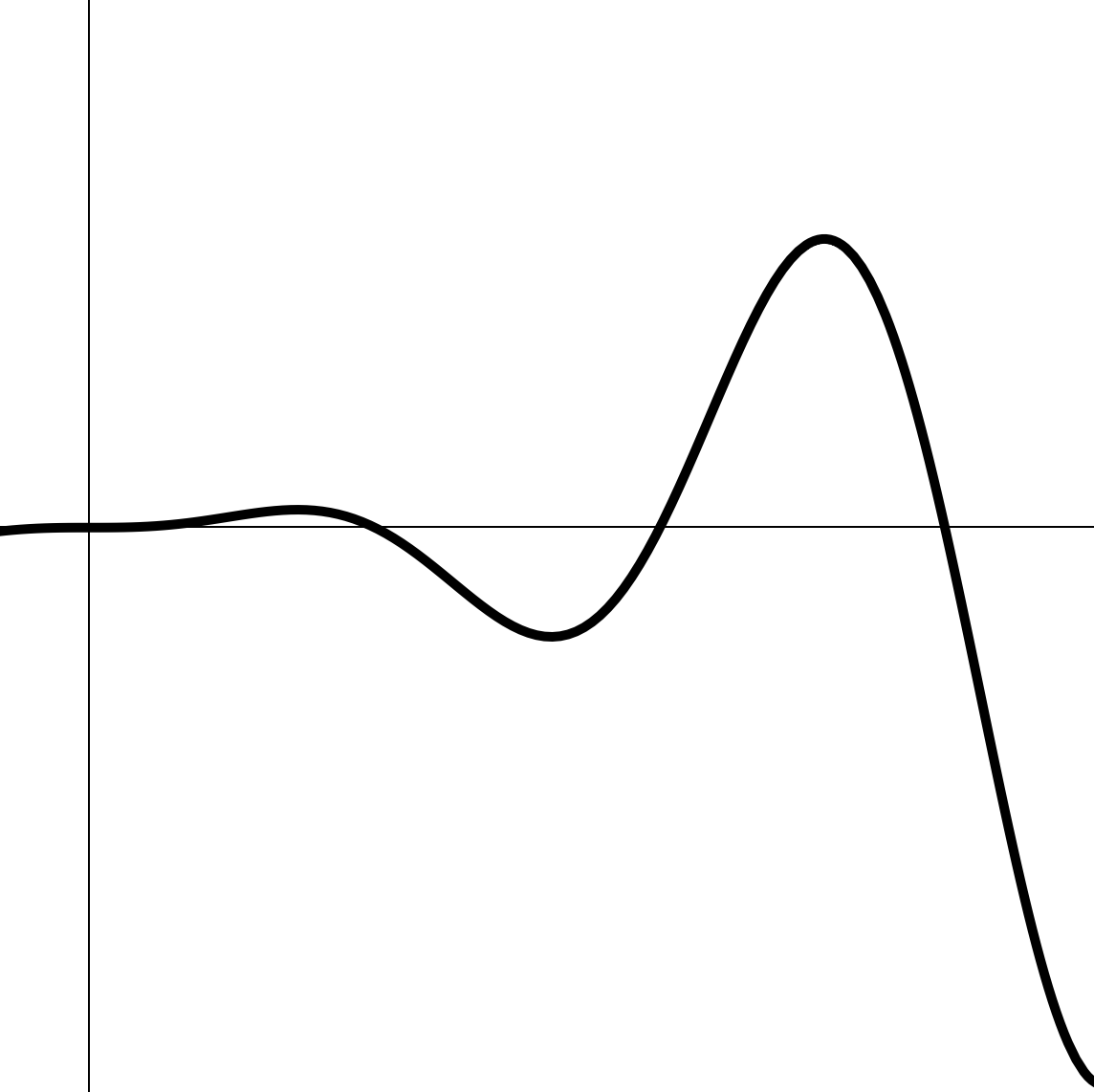


оператор предела
аргумент предела
значение предела
или:
Задача 1. Вычислить пределы
А есть ли разница, с какой стороны приближаться?
Конечно есть! И опять эта функция ...
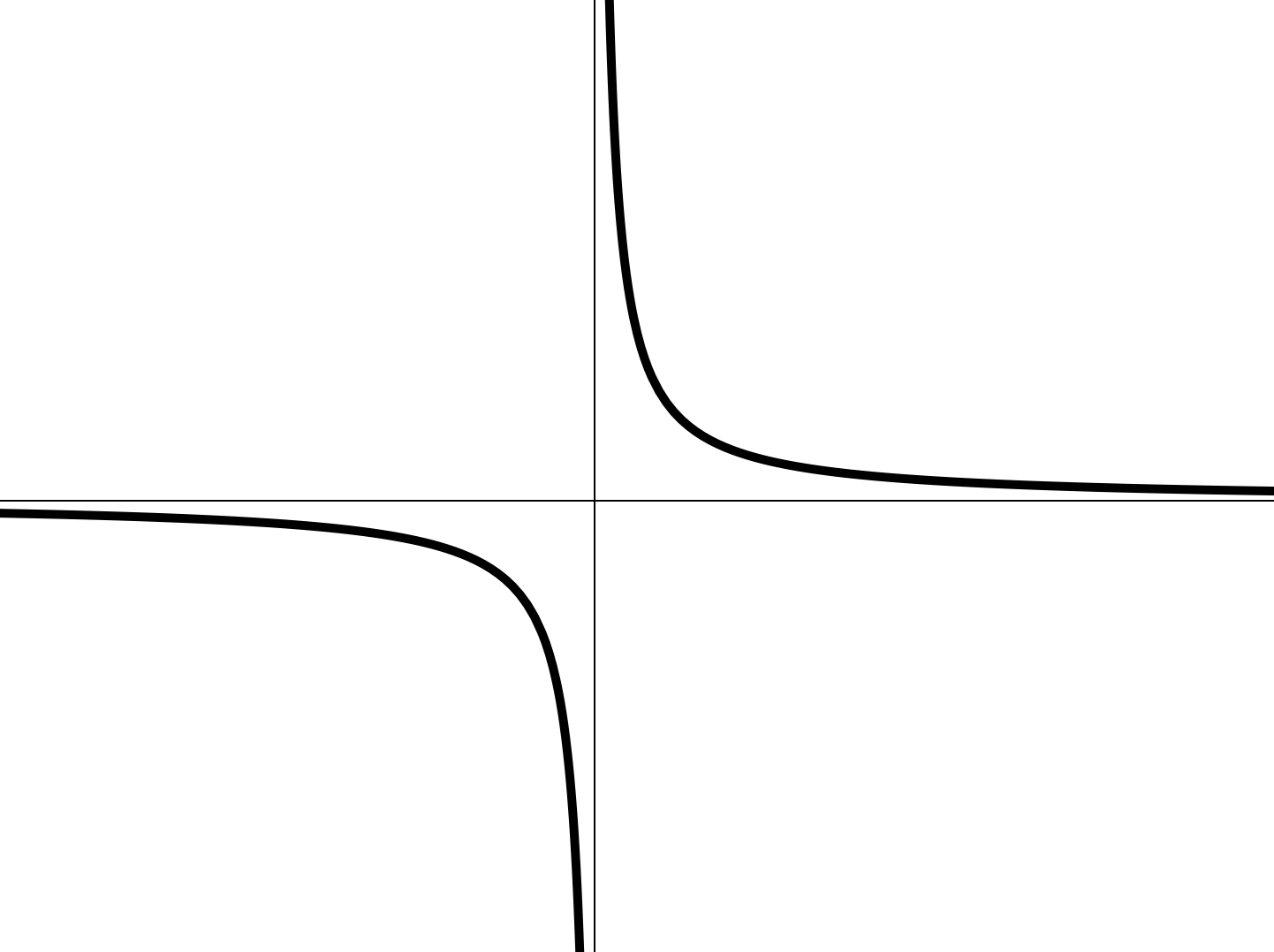
приближение слева:
*стремится к
приближение слева:
*стремится к
Левосторонний и правосторонний предел

Левосторонний предел:
Правосторонний предел:
Первый замечательный предел
Рассмотрим функцию
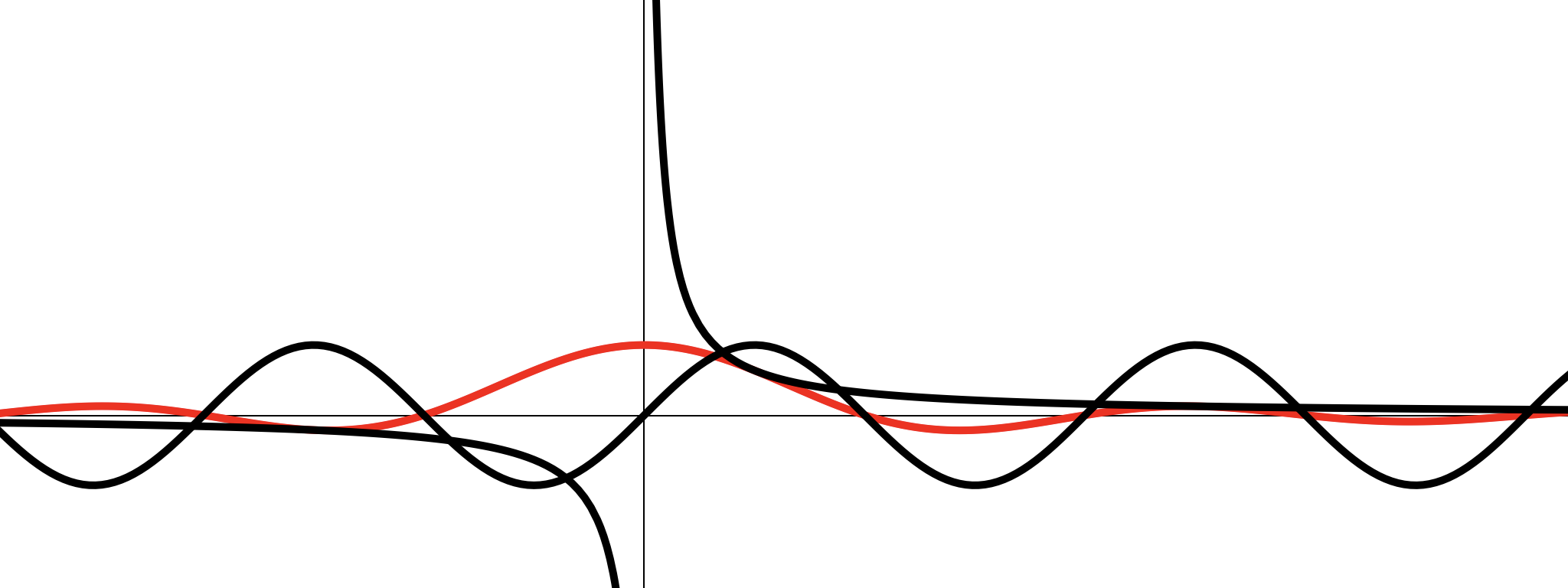
Точка разрыва
Второй замечательный предел
Рассмотрим функцию
Точка разрыва при . Но при сближении что слева, что справа к нулю: , .
Свойства пределов (1)
1.
2.
3.
4.
5.
где
Свойства пределов (2)
1.
2.
где