Цилиндр, конус, шар

11 класс

 

vkrysanov320@gmail.com

Понятие цилиндра

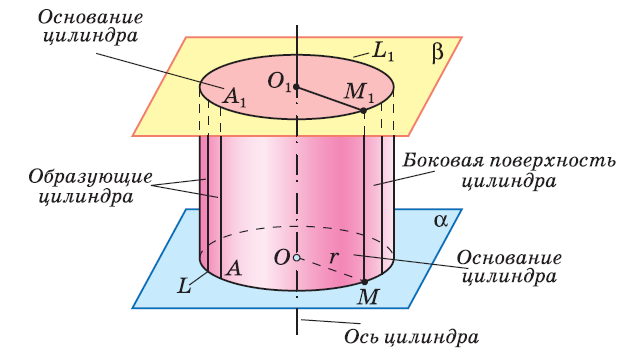
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами   и     , называется цилиндром.

L
L_1

Радиус цилиндра    — радиус основания цилиндра.

Диаметр цилиндра     — это диаметр основания цилиндра.

Высота цилиндра     — это расстояние между основаниями цилиндра.

Ось цилиндра — это прямая          , которая проходит через центры оснований цилиндра.

Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.

r
d
h
OO_1

Понятие цилиндра (2)

Цилиндром (прямым круговым) называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону (*).

* В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания перпендикулярны образующей.

но так бывает не всегда ...

Виды цилиндров

Наклонный круговой

Прямой круговой

окружность

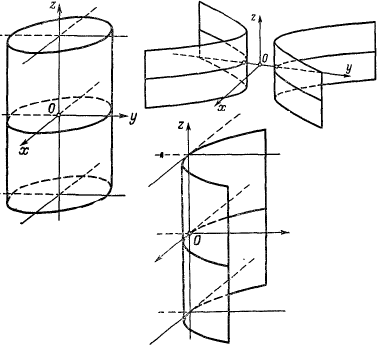
Прямой эллиптический

Прямой параболический

Прямой гиперболический

\begin{cases} \\ \\ \\ \\ \\ \\ \end{cases}
\begin{cases} \\ \\ \\ \\ \\ \\ \end{cases}

«школьные цилиндры»

«не школьные цилиндры»

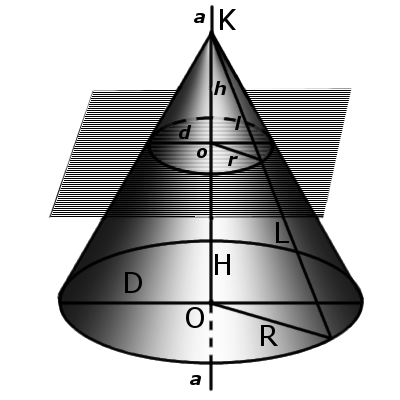
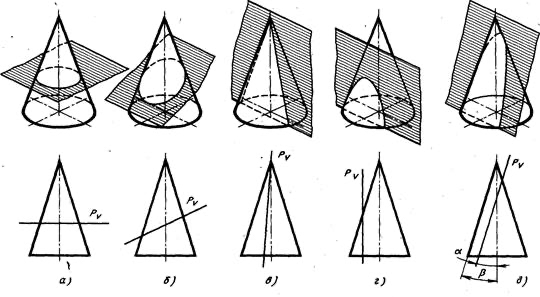
Сечения цилиндра

Сечение цилиндра плоскостью, перпендикулярной к оси

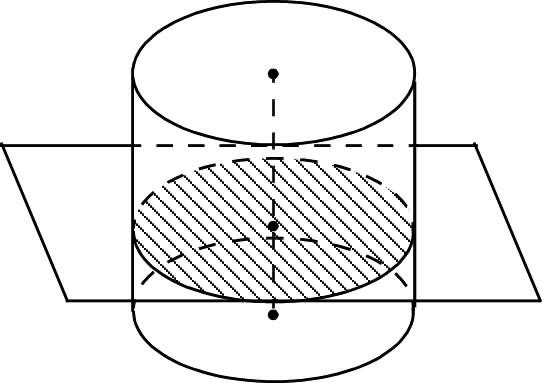
Так как цилиндр является телом вращения, то любое его перпендикулярное сечение есть круг, а перпендикулярное сечение боковой поверхности цилиндра — окружность; центры этих окружностей и кругов — точки пересечения секущих плоскостей и оси цилиндра

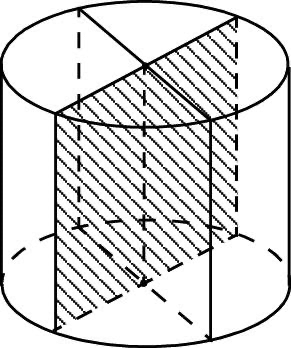
Осевое сечение цилиндра

Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра. При этом все осевые сечения цилиндра — равные между собой прямоугольники. Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром

Сечения цилиндра (2)

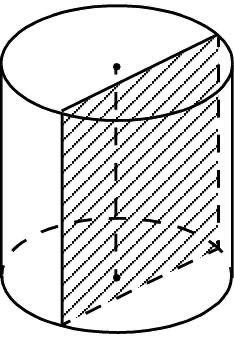
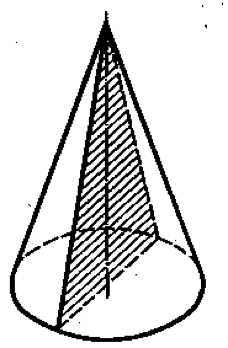
Сечение цилиндра плоскостью, параллельной его оси

Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра.

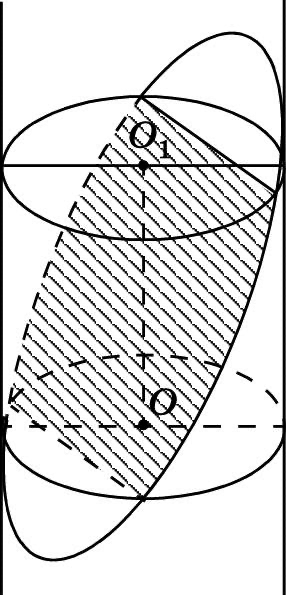
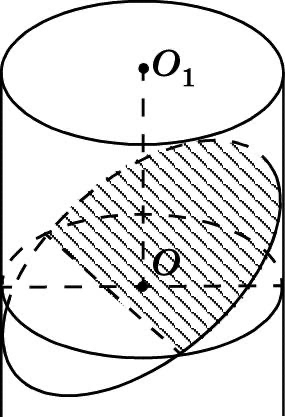
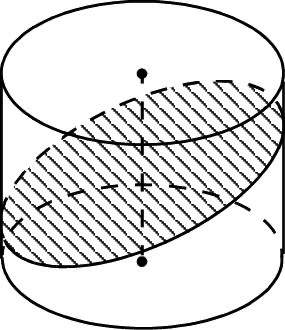
Сечение цилиндра плоскостью, неперпендикулярной к оси

Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс или его некоторая часть

Развёртка цилиндра

2\pi r
r
h
A
B
r
h
A \rightarrow
B \rightarrow
\rightarrow B
\rightarrow A
\times 2
S_{\text{бок}} = 2\pi r h
S_{\text{осн}} = \pi r^2
S_{\text{полн}} = 2\pi r h + 2\pi r^2
= 2\pi r (r + h)

Задачи

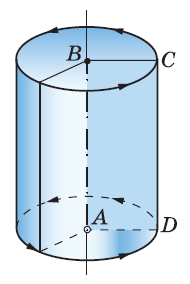
— ось цилиндра,                    — осевое сечение цилиндра.

OO_1
AA_1B_1B

1. Найти высоту и радиус основания цилиндра.

2. Дано:

Найти 

\angle O_1EO = 45 ^\circ, \angle EOC = 60^ \circ.
S(CO_1D).

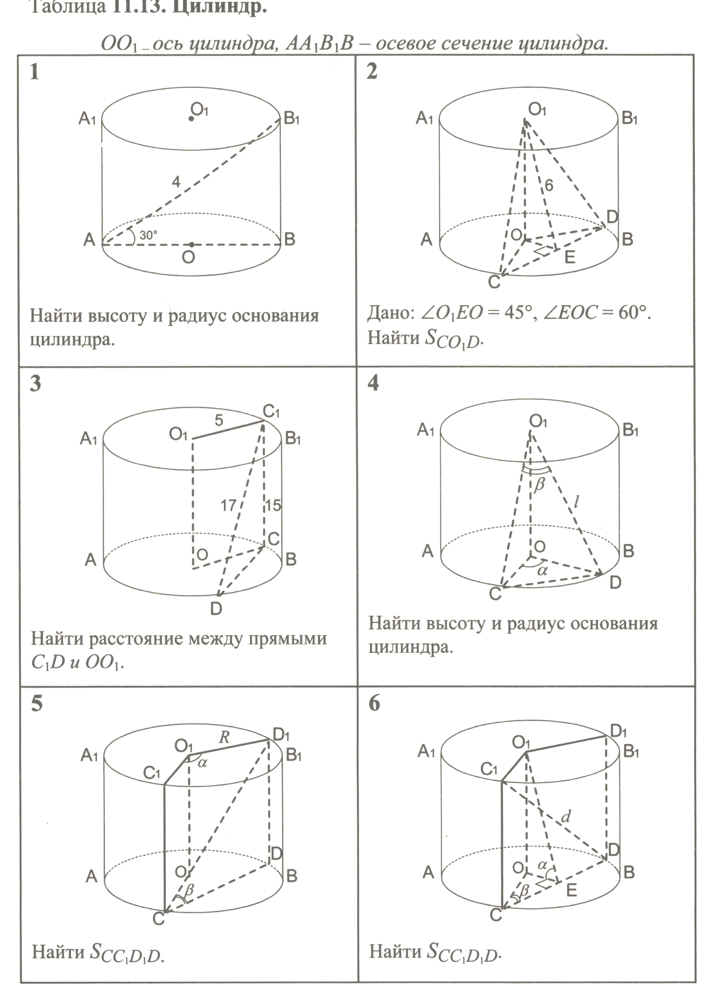
3. Найти расстояние между прямыми          и

C_1D
OO_1.

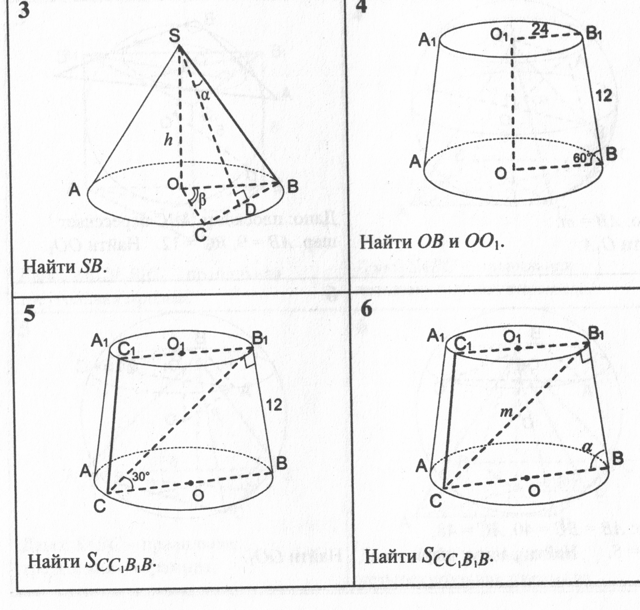
Задачи (2)

4. Высота цилиндра равна 8, радиус равен 5. Найти площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3.

 

5. Высота цилиндра равна 12, а радиус основания равен 10. Цилиндр пересечен плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найти расстояние от оси цилиндра до секущей плоскости.

Задачи (3)

6. Высота цилиндра равна 3, а радиус основания равен 13.

а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.

б) Найдите расстояние от плоскости сечения до центра основания цилиндра.

 

7.  Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно 

а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

 

\sqrt{730}.

Задачи (4)

8. Прямоугольник              и цилиндр расположены таким образом, что          — диаметр верхнего основания цилиндра, а         лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом      .

а) Докажите, что               — квадрат.

б) Найдите длину той части отрезка       , которая находится снаружи цилиндра, если радиус цилиндра равен         

 

\sqrt{2}.
ABCD
AB
CD
60^\circ
ABCD
BD

Задачи (на дом)

9. Прямоугольник              и цилиндр расположены таким образом, что         — диаметр верхнего основания цилиндра, а         лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом      .

а) Докажите, что               — квадрат.

б) Найдите длину той части отрезка       , которая находится снаружи цилиндра, если радиус цилиндра равен 


4.
ABCD
AB
CD
60^\circ
ABCD
BD

Понятие конуса

Тело, ограниченное конической поверхностью и кругом с границей     , называется конусом.

L

Вершина конуса — это точка (    ), из которой исходят лучи.

Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса.

P
l

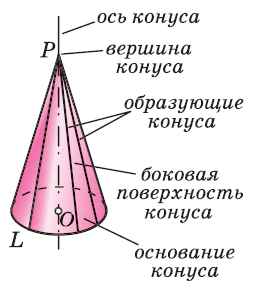
Высота конуса (  ) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Образующей конуса (  ) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Ось конуса — это прямая       , проходящая через вершину конуса и центр основания конуса.

Направляющая конуса — это кривая, которая описывает контур основания конуса.

h
PO

Понятие конуса (2)

Конусом (прямым круговым) называется фигура, полученная при вращении прямоугольного треугольника вокруг одного из его катетов (*).

* В большинстве случаев под конусом подразумевается прямой круговой конус, у которого направляющая — окружность, а ось перпендикулярна основанию и совпадает с высотой.

но так бывает не всегда ...

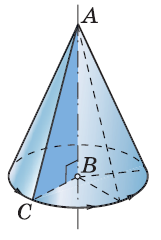
Виды конусов

Наклонный круговой

Прямой круговой

окружность

Усечённый круговой конус

окружность

окружность

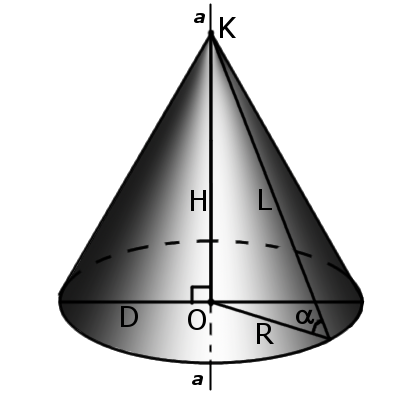
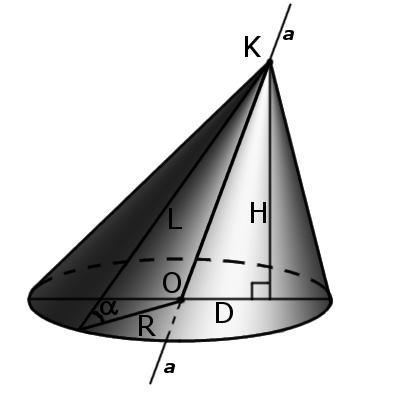
Сечения конуса

Если прямой круговой конус рассечь плоскостью, параллельной основанию, то линия пересечения боковой поверхности конуса с плоскостью будет окружностью.

Сечение плоскостью параллельной основанию

Осевое сечение конуса

Если секущая плоскость проходит через через ось конуса, то сечение представляет собой равнобедренный треугольник.

Сечение конуса плоскостью проходящей через вершину и хорду основания

Если конус рассечь плоскостью, проходящей через его вершину, и хорду основания, то это сечение представит собой равнобедренный треугольник.

Сечения конуса (2)

Если конус рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности конуса с плоскостью будет эллипсом.

Если на поверхности конуса можно провести две образующие параллельно пересекающей его плоскости, то такая плоскость пересечет боко­вую поверхность конуса по гиперболе.

Если плоскость пересекает конус параллельно одной образующей, то боковая поверхность конуса пересечется этой плоскостью по парабо­ле.

Развёртка конуса

h
P
r
S_{\text{полн}} = \pi r l + \pi r^2
= \pi r (l + r)
r
S_{\text{осн}} = \pi r^2
O
R
l
l
\alpha
\begin{cases} S_{\text{сек}} = \frac{\pi R^2}{360} \alpha; \\ L = \frac{\pi R}{180} \alpha;\\ L = 2\pi r; \end{cases}
\Rightarrow
\alpha = \frac{360r}{R}
L
\Rightarrow
S_\text{бок} = S_{\text{сек}} = \pi R r = \pi lr
S_\text{бок} = \pi lr

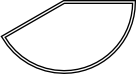
Развёртка усечённого конуса

S_{\text{полн}} = \pi(r+r_1)l + \pi r_1^2 + \pi r^2
r
S_{\text{осн}} = \pi r^2
S_\text{бок} = \pi r \cdot PA - \pi r_1 \cdot PA_1 =
r_1
S_{\text{осн}} = \pi r_1^2
l
\begin{cases} \\ \\ \\ \end{cases}
L
= \pi r \cdot (PA_1 + AA_1) - \pi r_1 \cdot PA_1=
= \pi r l + \pi (r- r_1) \cdot PA_1.

Прямоугольные треугольники (            и           ) подобны:

PA_1O
PAO
\frac{PA_1}{PA} = \frac{r_1}{r} \Rightarrow \frac{PA_1}{PA_1 + l} = \frac{r_1}{r} \Rightarrow PA_1 = \frac{lr_1}{r-r_1}.
\Rightarrow S_\text{бок} = \pi r l + \pi (r- r_1) \cdot \frac{lr_1}{r-r_1} = \pi(r+r_1)l.

Задачи

SO
SO, OB.
O_1

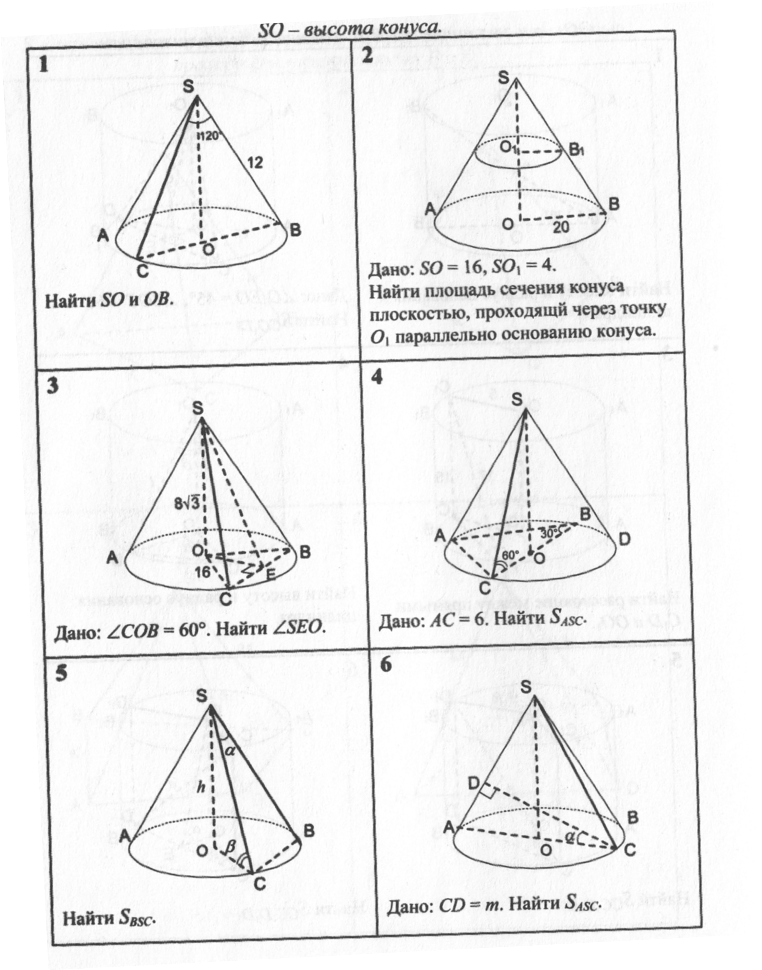
— высота конуса.

1. Найти: 

SO = 16, SO_1 = 4.

2. 

Найти: площадь сечения конуса плоскостью, проходящей через точку параллельно основанию конуса.

\angle SEO.

3.                            

Найти: 

\angle COB = 60^\circ.
S(ASC).

4.                            

Найти: 

AC=6.

Задачи (2)

SO
OB, OO_1.

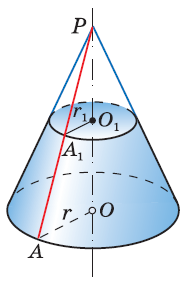
— высота конуса;             — центры оснований усеченного конуса.

5. Найти: 

O, O_1
S(CC_1B_1B).

6. Найти: 

Задачи (3)

7. На окружности основания конуса с вершиной     отмечены точки           и      так, что                         Медиана         треугольника            пересекает высоту конуса.

а) Точка      — середина отрезка        . Доказать, что угол              прямой.

б) Найти угол между прямыми         и       , если 

 


8. В конусе с вершиной     и центром основания       радиус основания равен       , а высота равна            . Точки      и      — концы образующих,      — середина        ,      — точка в плоскости основания такая, что прямая           параллельна прямой        .

а) Доказать, что             — прямой угол.

б) Найти угол между          и плоскостью основания, если дополнительно известно что 

S
A, B
AM
C
AB=BC.
ASC
MNB
N
AM
AC
SB
AS=2, AC = \sqrt{6}.
S
O
3\sqrt{41}
A
B
M
SA
N
MN
SB
ANO
MB
AB=10.
13

Задачи (4)

9. Площадь боковой поверхности конуса равна        , а площадь основания равна        . Найти длину образующей конуса.

 

10. Площадь боковой поверхности конуса равна        , а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна         . Найти высоту усеченного конуса, если высота исходного конуса равна     .

 

11. На высоте конуса с вершиной    , центром основания      и радиусом основания отметили точку такую      , что расстояние от неё до основания равно                    . Известно, что угол между образующей конуса и плоскостью основания равен       . Найти площадь сечения конуса, проходящего через точку      и параллельного основанию конуса.

48\pi
36\pi
48\pi
36\pi
10
A
C
R
Q
4\sqrt{3} - \frac{\sqrt{3}}{\pi}
60^\circ
Q

Задачи (на дом)

7. На окружности основания конуса с вершиной     отмечены точки           и      так, что                         Медиана         треугольника            пересекает высоту конуса.

а) Точка      — середина отрезка        . Доказать, что угол              прямой.

б) Найти угол между прямыми         и       , если 

 


8. Дан прямой круговой конус с вершиной      . Осевое сечение конуса — треугольник с углом          при вершине       . Образующая конуса равна           Через точку  проведено сечение конуса, перпендикулярное одной из образующих.

а) Доказать, что получившийся в сечении треугольник — тупоугольный.

б) Найти расстояние от центра        основания конуса до плоскости сечения.

S
A, B
AM
C
AB=BC.
ASC
MNB
N
AM
AC
SB
AS=2, AC = \sqrt{10}.
M
M
120^\circ
M
2\sqrt{3}.
O

Сфера и шар

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (центра сферы (точка     )).

Радиус сферы (    ) — расстояние, от центра сферы до любой точки сферы.

Диаметр сферы (    ) — отрезок, соединяющий две точки сферы и проходящий через центр сферы.

O
R
D

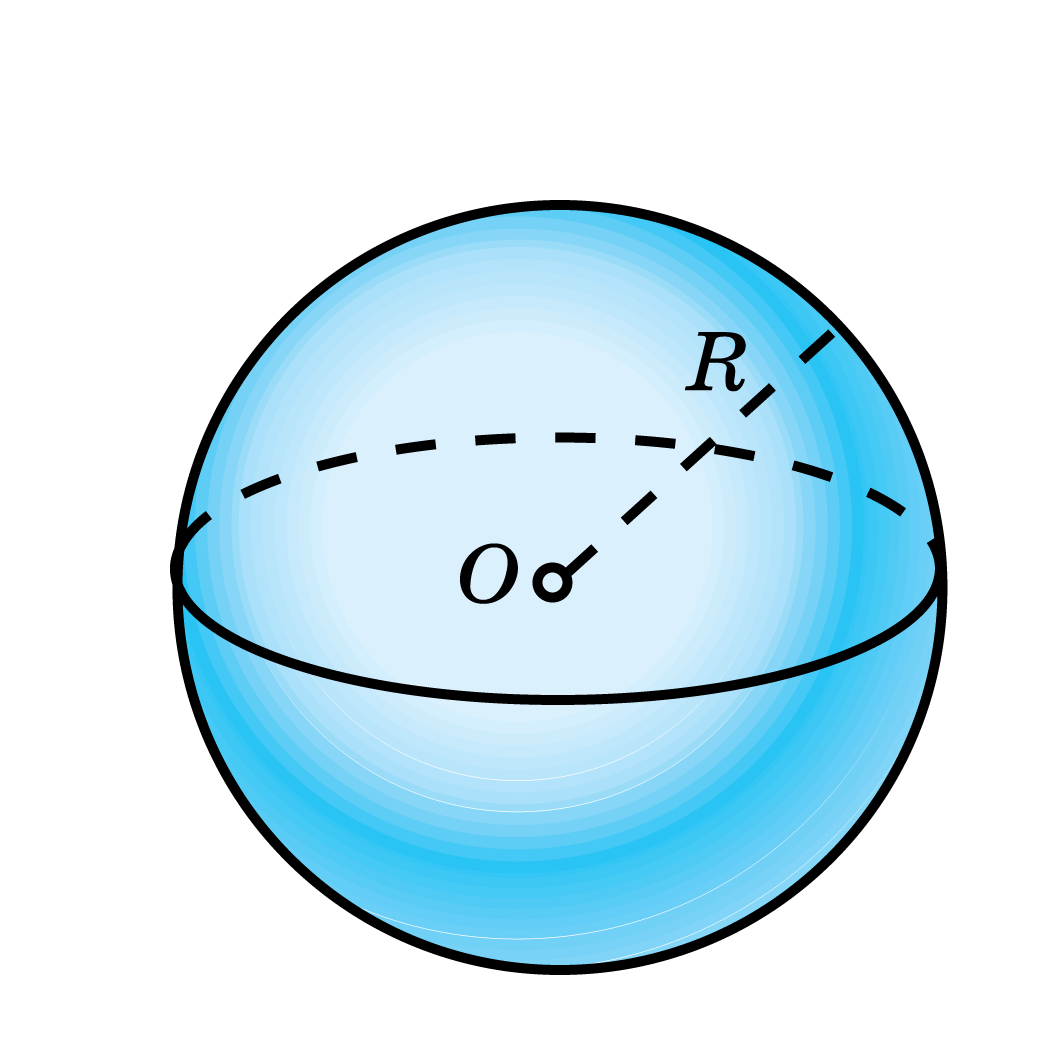
* Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

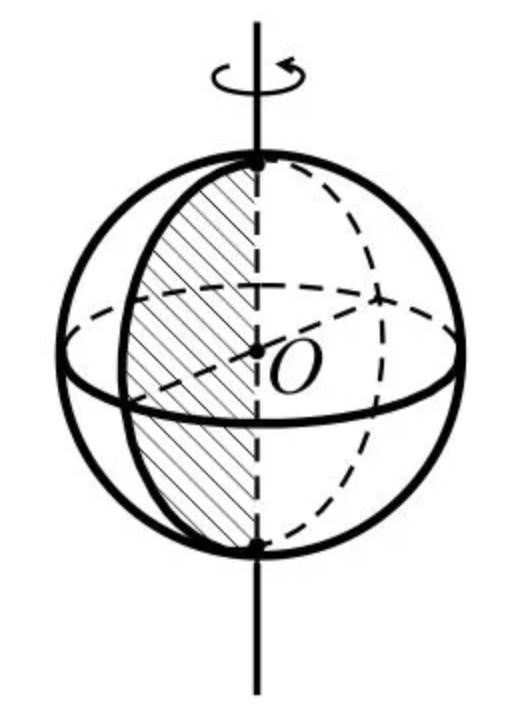
Тело, ограниченное сферой, называется шаром.

Центр, радиус и диаметр сферы называются так же центром, радиусом, диаметром шара.

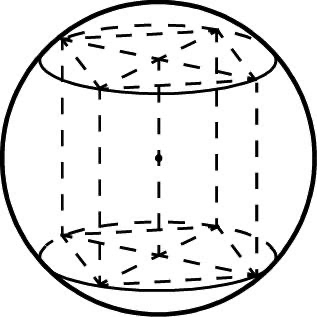
Изображение сферы

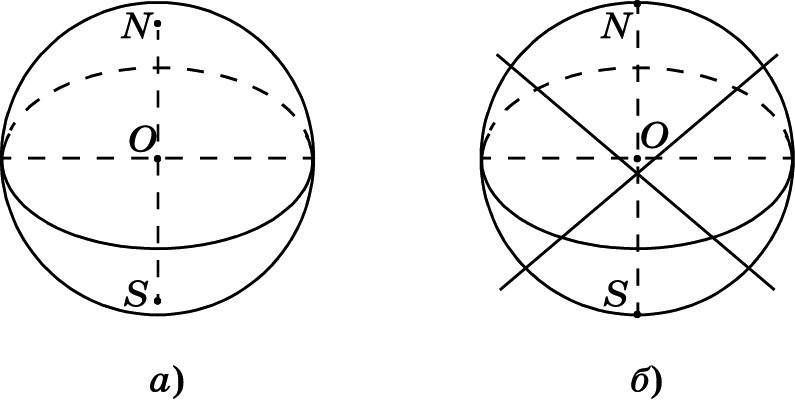
Точки      и      — полюсами сферы.

Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси)       ,называется экватором.

NS
N

Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией.

S

* Типичная ошибка при изображении сферы в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

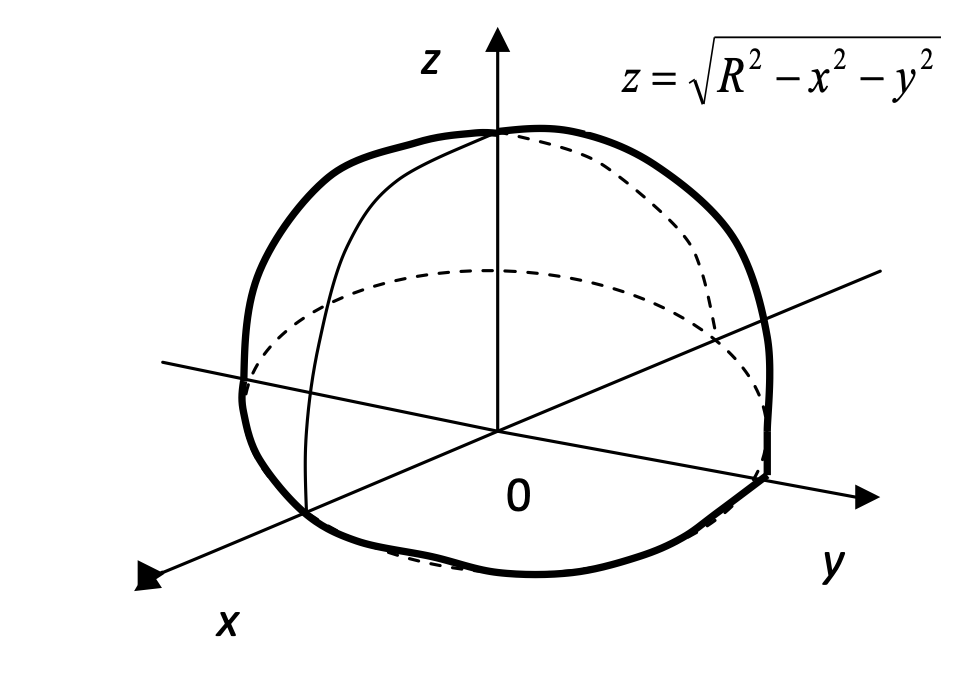
Уравнение сферы

MC = \sqrt{(x-x_0)^2 + (y - y_0)^2 + (z - z_0)^2}

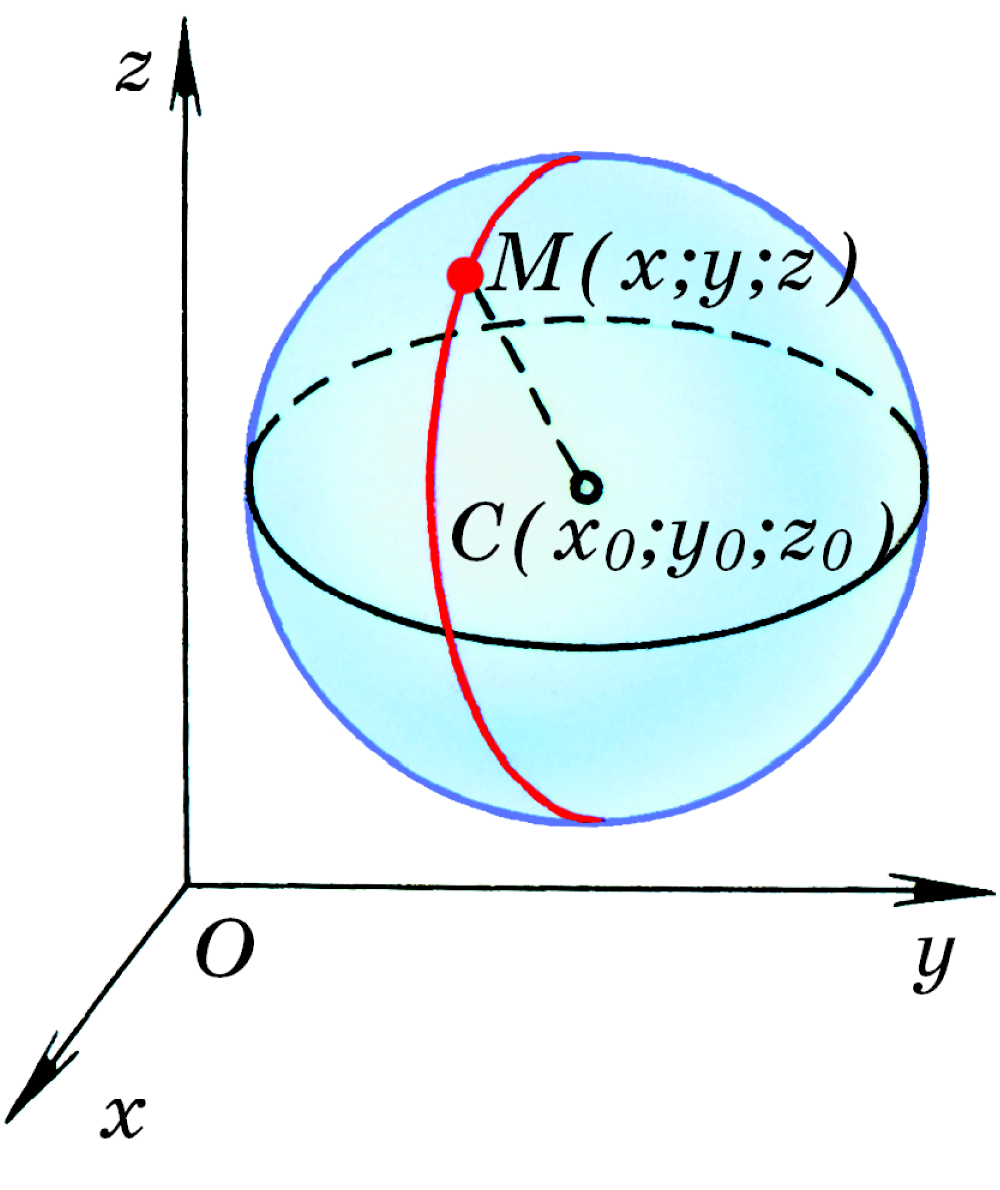
расстояние от произвольной точки                   до точки    .

M(x;y;z)
C
  • если точка                  лежит на данной сфере, то
  • иначе:
M(x;y;z)
MC^2 = R^2.
MC^2 \ne R^2.
(x-x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = R^2

в прямоугольной системе координат уравнение сферы радиуса

с центром                      имеет вид:

R
C(x_0; y_0; z_0)

Взаимное расположение сферы и плоскости

\begin{cases} z = 0; \\ x^2 + y^2 + (z-d)^2 = R^2; \end{cases} \Rightarrow x^2 + y^2 + d^2 = R^2 \Rightarrow x^2 + y^2 = R^2 - d^2.
R > d:
R = d
R < d

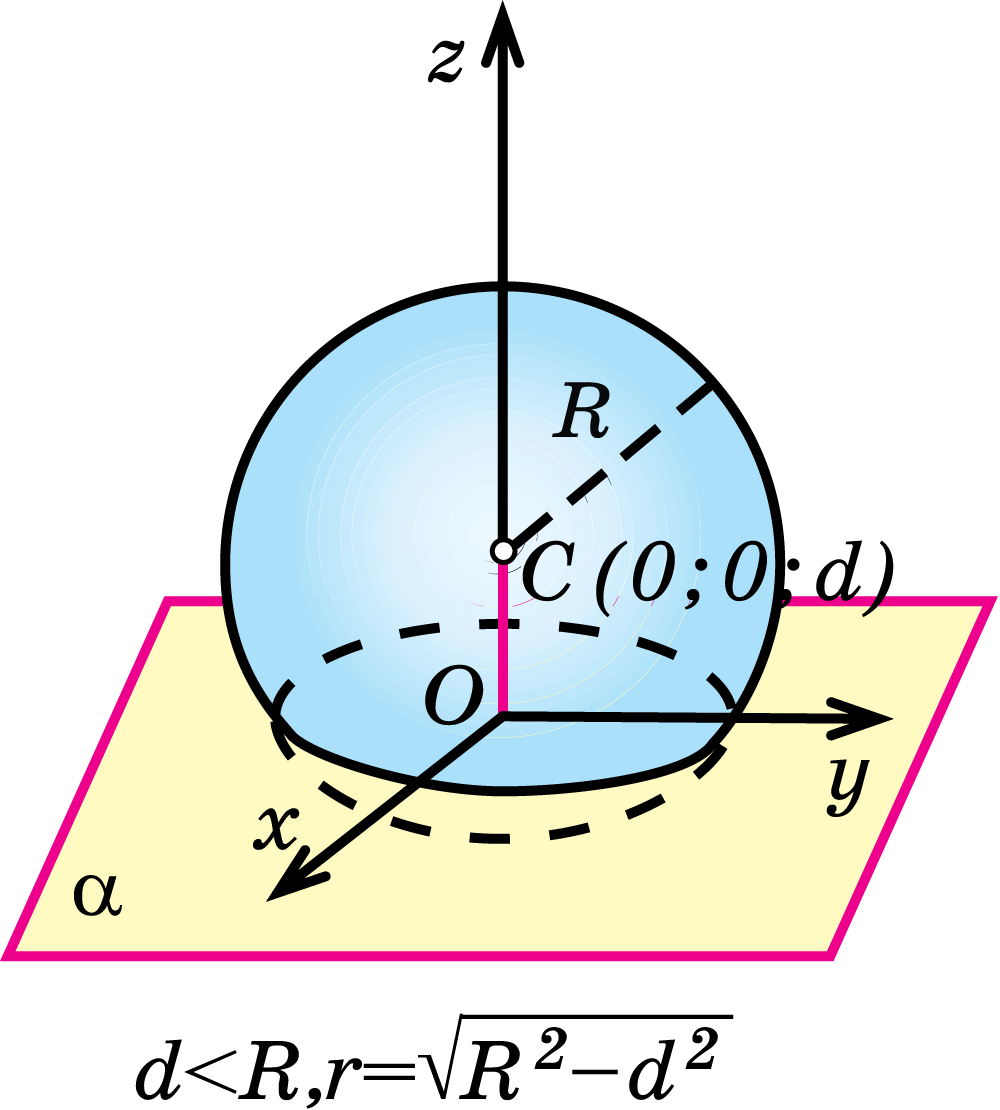
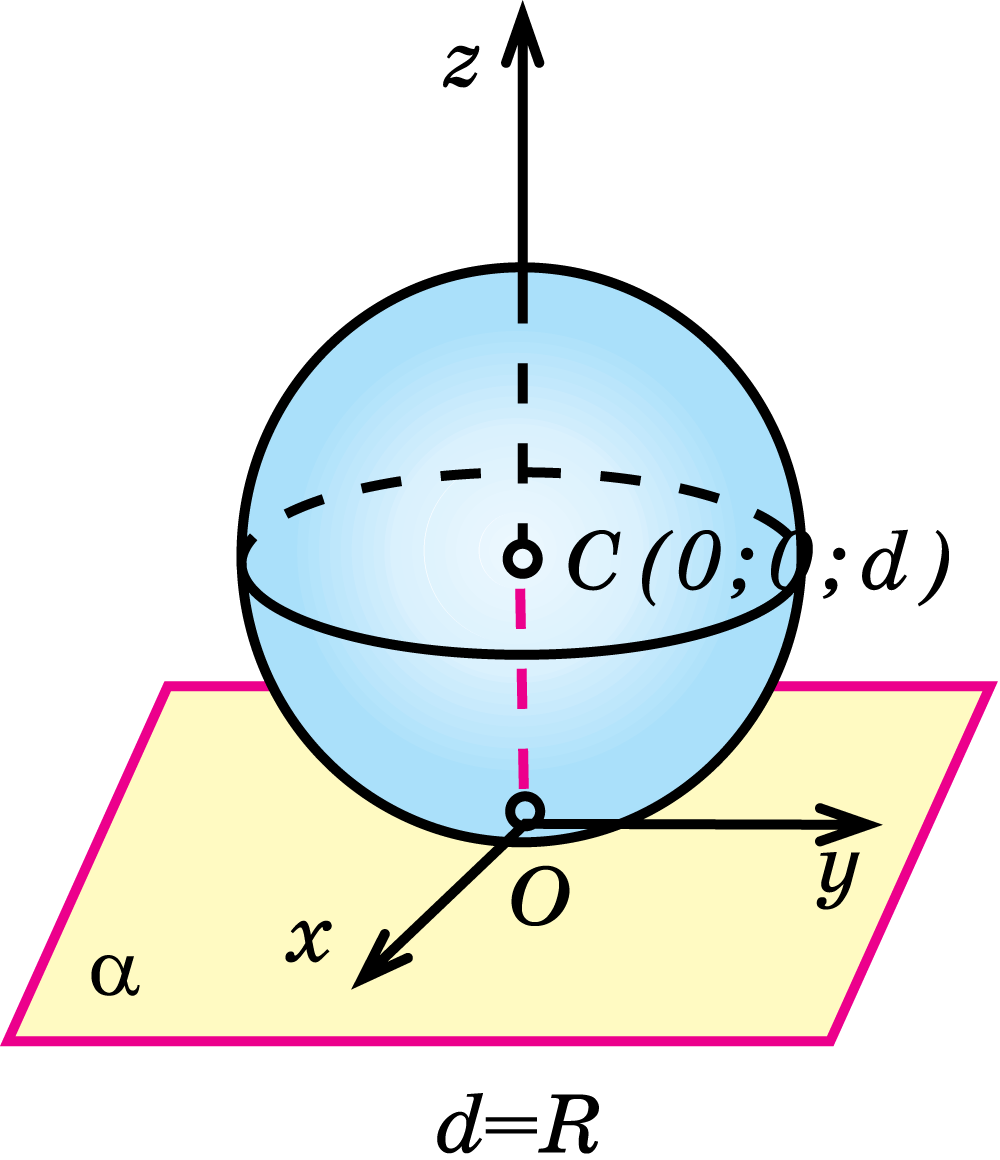
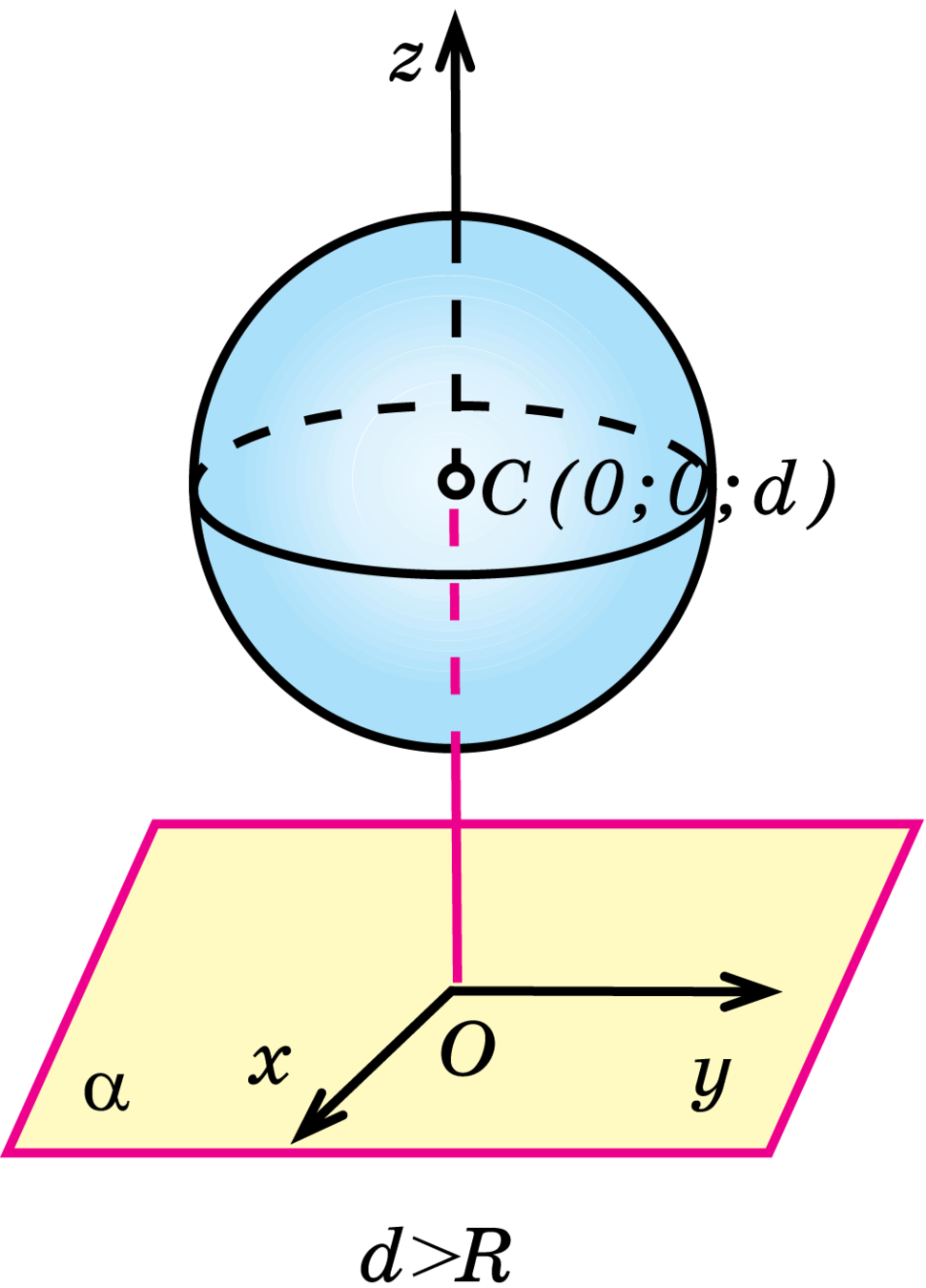
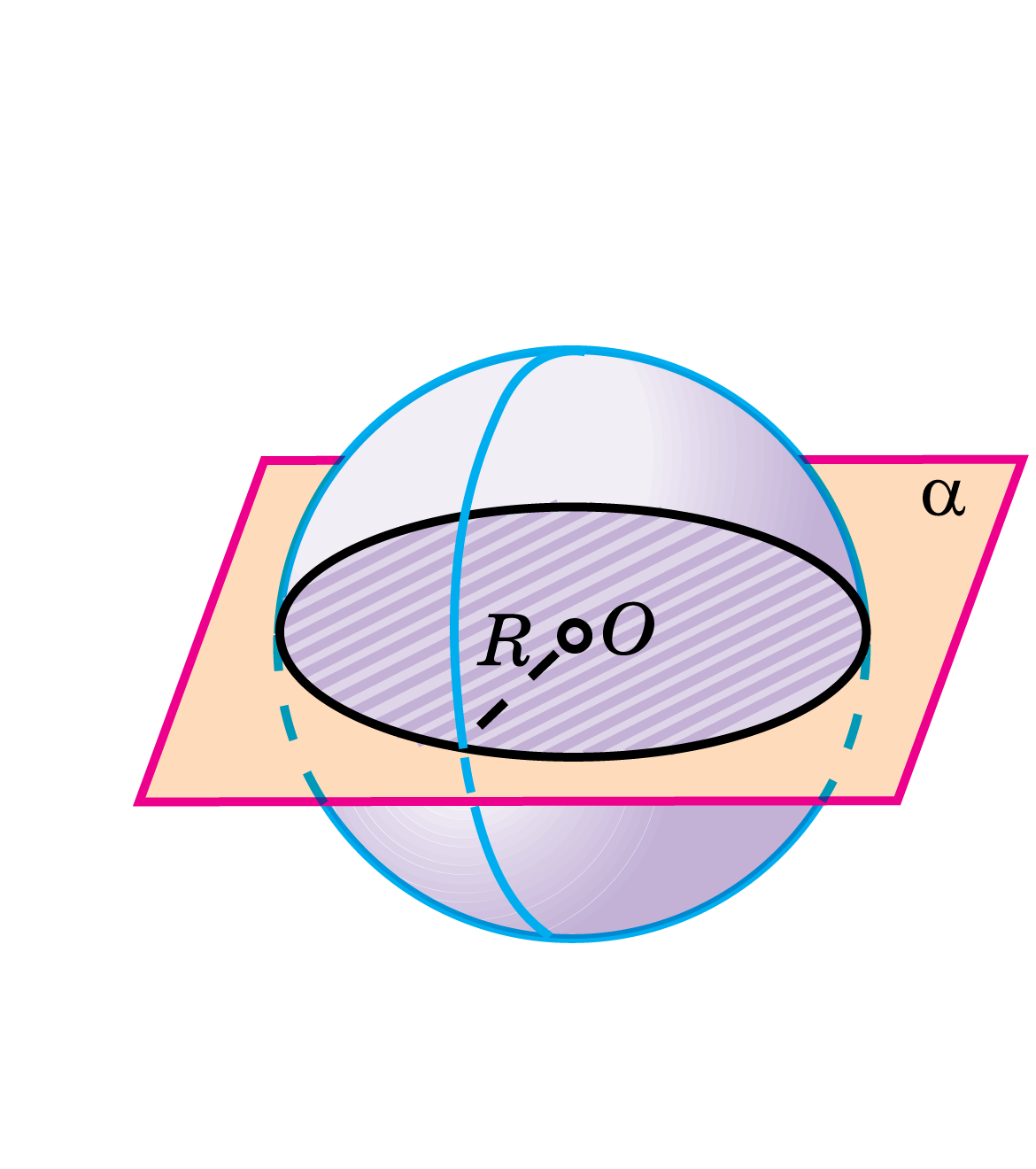
Сечение шара плоскостью есть круг

r = \sqrt{R^2 - d^2}
d = 0:
r = R

I(a).

I(b).

II.

III.

Задачи

Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен     .

Найти:

    а) площадь получившегося сечения;

    б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара;

    в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.

R

Плоскость, касательная к сфере и шару

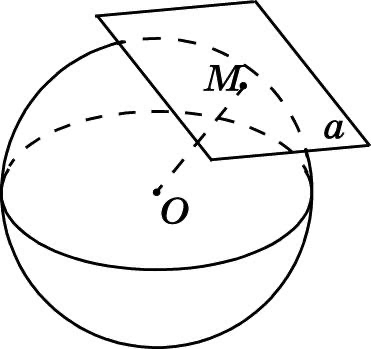
Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания.

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере;

Эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Вписанные и описанные шары и сферы (1)

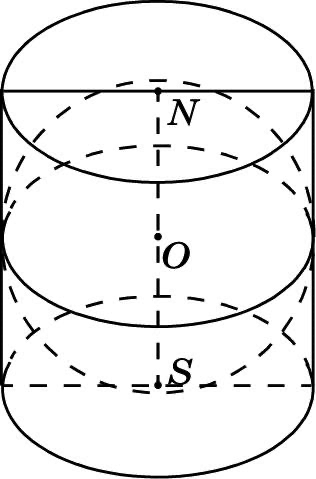
Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара

Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара

* Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.

* Шар можно вписать только в такой цилиндр, в котором диаметр основания равен высоте.

Вписанные и описанные шары и сферы (2)

Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара

Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

* Около любого конуса можно описать шар. Центр шара находится в точке пересечения высоты конуса и серединного перпендикуляра образующей конуса.

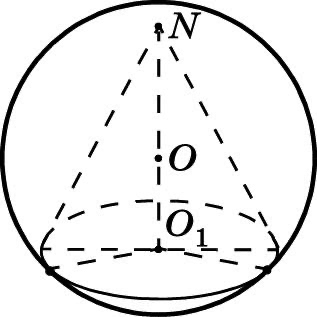
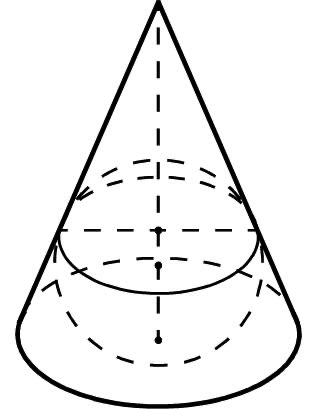
*В любой конус можно вписать шар. Центр шара находится в точке пересечения высоты конуса и биссектрисы угла образующей конуса с основанием конуса.

Вписанные и описанные шары и сферы (3)

Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара.

Шар называется вписанным в многогранник, если он касается всех граней многогранника.

*Для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг.

*Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.

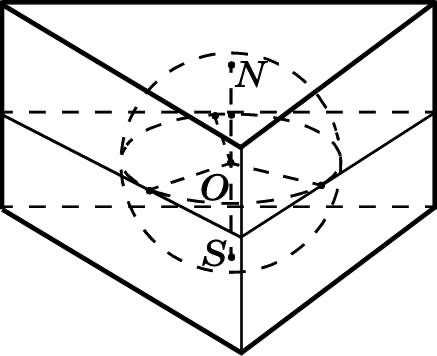
Площадь сферы

S = 4\pi R^2
x^2 + y^2 + z^2 = R^2
\Rightarrow z = f(x; y) = \sqrt{R^2 - x^2 - y^2}
\iint\limits_D \sqrt{1 + \bigl(f(x;y)'_x\bigr)^2 + \bigl(f(x;y)'_y\bigr)^2}dxdy \Rightarrow \frac{1}{2}S = \int\limits_{-R}^R \bigl(\int\limits_{-\sqrt{R^2 - x^2}}^{R^2 - x^2} \frac{R}{R^2 - x^2 - y^2}dy\bigr)dx
\Rightarrow S = 2\int\limits_{0}^{2\pi} \bigl(\int\limits_0^R \frac{R}{R^2 - \rho} \rho d\rho \bigr)d\varphi = 2R\int\limits_{0}^{2\pi} -\sqrt{R^2 - \rho^2} \Bigl|^R_0\Bigr. d\varphi = 2R\int\limits_{0}^{2\pi}Rd\varphi = 4\pi R^2.

Уравнение сферы:

Задачи

1. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найти площадь полной поверхности цилиндра.

 

2. Шар вписан в цилиндр. Площадь поверхности шара равна 12. Найдите площадь полной поверхности цилиндра.

 

3. Найдите радиус шара, описанного около

    а) куба с ребром а;

    б) правильного тетраэдра с ребром а.

4. Найти радиус шара, в который вписана правильная треугольная пирамида, все ребра которой равны 2

Задачи (2)

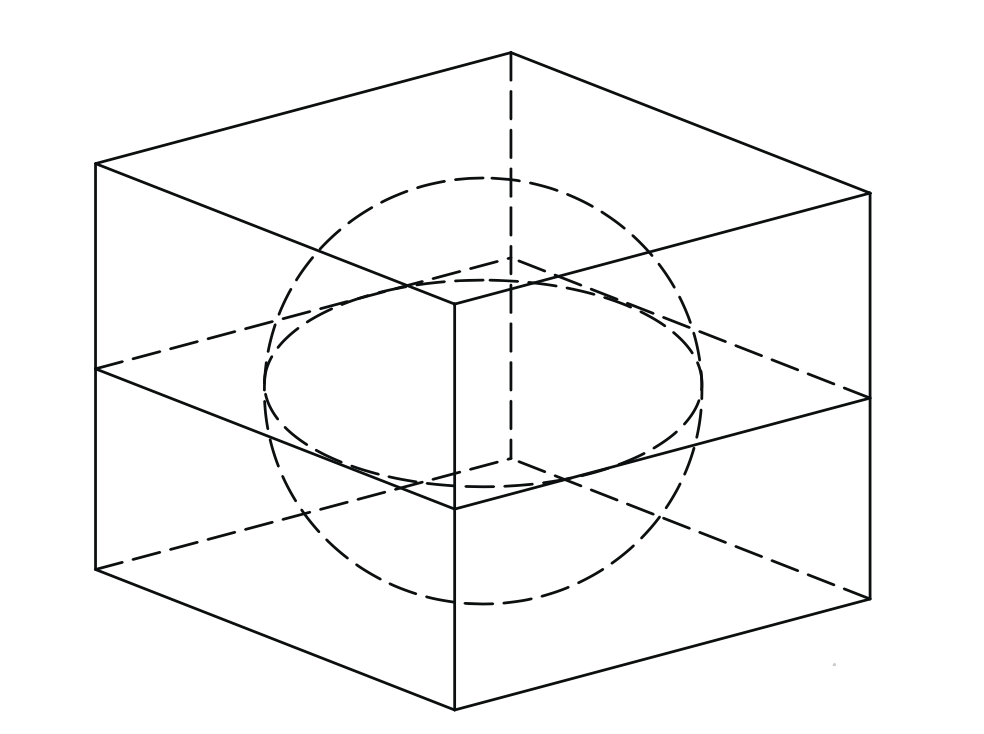
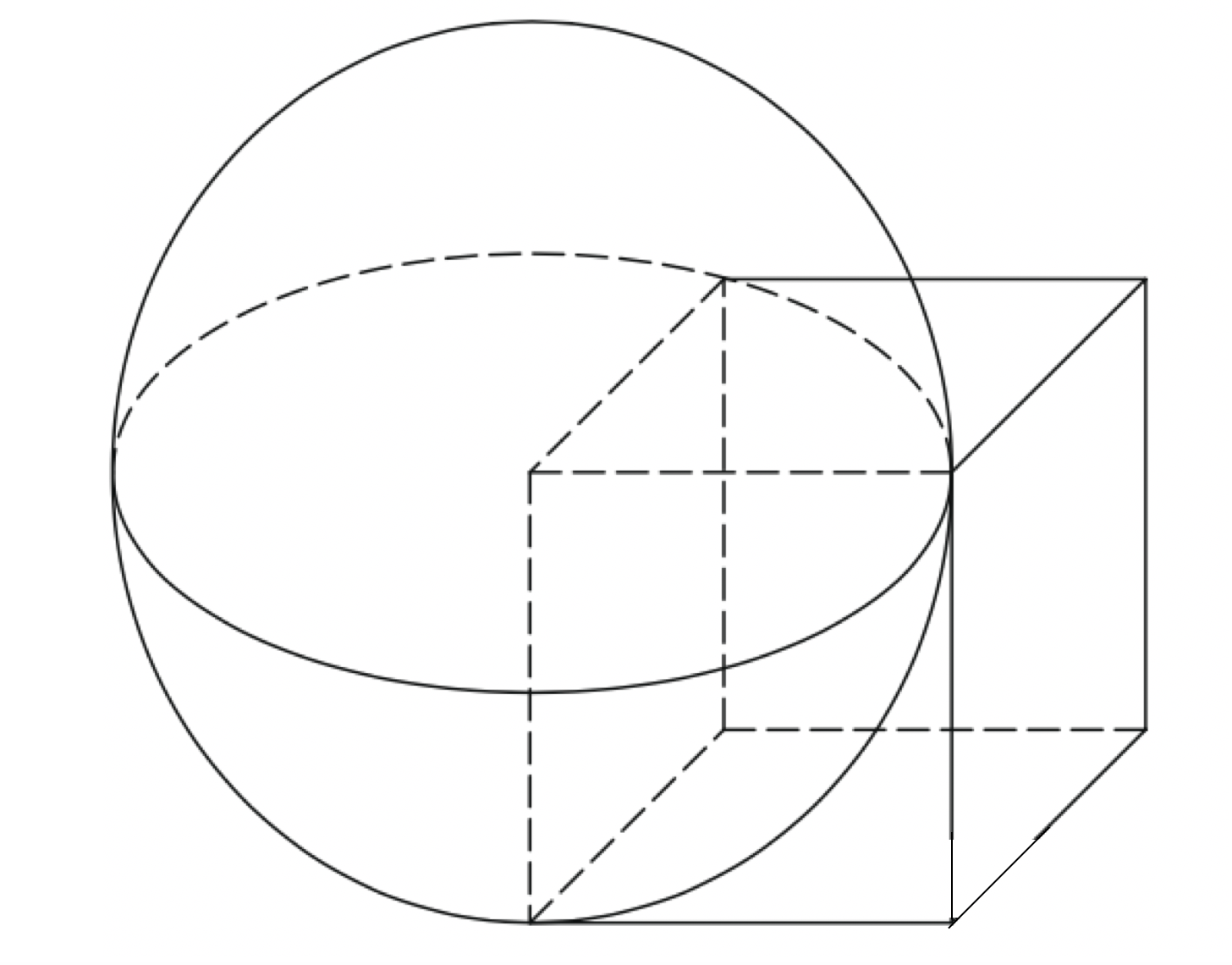
5. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

 

6. Вершина     куба  с ребром 1,6 является центром сферы, проходящей через точку     . Найдите площадь части сферы, содержащейся внутри куба. В ответе запишите эту величину деленную на    .

 

 

A
A_1
\pi

Задачи (3)

7. Площадь поверхности шара равна     . На расстоянии        от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.

8. Точка      — центр сферы, точка      — центр круга     , полученного в результате сечения этой сферы плоскостью. Точка      лежит на     ,                    , где      — точка на сфере. Площадь     равна 100,                            ,                            . Найти площадь сферы.

 

9.                           — правильная треугольная призма, боковое ребро которой равно 8. Чему равен радиус описанного шара, если                      .

 

10. В правильную треугольную призму вписана сфера. Расстояние от центра сферы до ребра основания равно         . Чему равен радиус сферы?

 

11. В правильную четырёхугольную пирамиду                    вписан шар с центром       и радиусом равным 1.                             . Чему равны двугранные углы при основаниях?

\frac{37}{\pi}
\frac{1}{2\pi}
D
A
L
B
L
AB \parallel CD
C
L
S_{ABCD} = \frac{240}{\pi \sqrt{3}}
\angle ADB = 30^\circ
ABCA_1B_1C_1
AB = 3\sqrt{3}
5\sqrt{2}
SABCD
Q
P_{ABCD} = 8\sqrt{3}

FIX IT

Задачи (4)

12.               — пирамида,                       .                                                 .                . Чему равен радиус описанного около пирамиды шара?

 

13. Радиус вписанного в куб шара равен 3 см. Чему равно ребро куба?

 

14. Ребро куба равно         . Чему равен радиус описанного около куба шара?

 

15*. В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найти площадь этой сферы.

 

16*. В правильную шестиугольную пирамиду, боковое ребро которой равно          а высота равна 1 вписана сфера. (Сфера касается всех граней пирамиды.) Найти площадь этой сферы.

SABC
AS \perp ABC
AB = BC = AC = 3\sqrt{3}
AS = 8
4\sqrt{3}
\sqrt{5}
Made with Slides.com