Математическая логика

10 класс

 

vkrysanov320@gmail.com

 

Математическая логика

Математическая логика — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний

Высказывание — это утверждение о чем-либо, которое может быть либо истинным, либо ложным.

Примеры высказываний:

  • Париж — столица Англии.
  • Карась не рыба.
  • Число 6 делится на 2 и на 3.
  • 5 < 6

Примеры не являющиеся высказываниями:

  • 5+5.
  • Уходя, гасите свет!
истинно
ложно

*Истину (True) обозначаем как единицу, ложь (False) как 0.

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика

Простые и сложные высказывания

Высказывание, представляющее собой одно утверждение принято называть простым. Сложное высказывание получается путём объединения простых высказываний, связанных союзами И, ИЛИ и частицей НЕ.

На улице идёт снег

На улице идёт снег и пасмурно

Высказывания обычно обозначают строчными латинскими буквами:

u, v, w, x, y, z.

Часто применяются регистры:

x_1, x_2, x_3, ...

Для примера выше:

— На улице идёт снег;

— На улице пасмурно.

x_1
x_2
x_1
x_1 \text{ и } x_2

(для первого примера)

(для второго)

Булева функция

Булева функция (логическая функция, функция алгебры логики) от     аргументов — в дискретной математике — отображение:

f : \underbrace{B \times B \times ... \times B}_{n} \rightarrow B
f : B^n \rightarrow B
n

или проще

B = \{0, 1\}

где                      — булево множество;

интерпретируют как логические значения «истинно» (True) и «ложно» (False)

    — арность функции.

n

* Аргументы этих функций будем называть логическими переменными

Таблицы истинности

f(x_1, x_2, ..., x_n)

Любую логическую функцию                              можно задать таблицей истинности, в левой части которой перечислены все возможные наборы значений её аргументов (то есть двоичных векторов длины     ), а в правой части — значения заданной функции на этих наборах.

n
0
\vdots
0
x_1
0
0
x_2
...
x_n
f
0...0
0
f_1
0...0
1
f_2
\vdots
\vdots
\vdots
\vdots
f_{n-1}
1...1
1...1
0
1
1
1
1
1
f_n

В таблице истинности наборы значений аргументов расположены в лексикографическом порядке

\underbrace{\text{\hspace{2.2cm}}}
2^n

Основные логические операции

Конъюнкция

Логическое «И» (конъюнкция) — операция, применяемая к двум операндам, т.е. бинарная операция. Выражение     и     записывается как                                                     или                . Конъюнкция задаётся следующей таблицей истинности:

A \cdot B, A \wedge B, A \&\& B, A \& B
A \text{ and } B
B
0
1
0
0
A
A \& B
1
0
1
1
1
0
0
0

Логическое «И», как не сложно понять из названия, образует выражение, которое истинно только тогда, когда истинны оба исходных выражения, входящих в его состав: и первое, и второе.

A
B
\&
A
B
A \& B

Дизъюнкция

Логическое «ИЛИ» (дизъюнкция) — ещё одна бинарная операция. Выражение     или     записывается как                                                или                       . Дизъюнкция задаётся следующей таблицей истинности:

A + B, A \vee B, A || B, A | B
A \text{ or } B
B
0
1
0
0
A
A | B
1
0
1
1
1
0
1
1

Логическое «ИЛИ» образует выражение, которое истинно тогда, когда истинно хотя бы одно исходных выражение, входящее в его состав: или первое, или второе.

A
B
1
A
B
A | B

Инверсия

A
!A
0
1
1
0

Отрицание (инверсия) — операция, применяемая к одному операнду, т.е. унарная операция. Выражение          записывается как                   или            . Операции отрицания задаётся следующей таблицей истинности:

\neg A, \overline{A}, A!
\text{not }A

Истинность выражения, построенного с помощью отрицания, противоположна истинности исходного выражения. Если     — истинно,      — ложно, и наоборот.

A
!A
\text{не } A
A
!A

Производные логические операции

Cтрогая дизъюнкция

Операция исключающего «ИЛИ» (строгая дизъюнкция, сложение по модулю 2) похожа на обычную дизъюнкцию. Её обозначают как                               или               . Операция задается следующей таблицей истинности:

A \oplus B, A\text{\textasciicircum}B
B
0
1
0
0
A
1
0
1
1
0
0
1
1
=1
A
B
A \oplus B
A\text{ xor }B
A \oplus B

Результат выполнения операции истинен тогда и только тогда, когда операнды не равны.

A \oplus B = !A \cdot B + A \cdot !B = (!A + !B) \cdot (A +B)

Импликация

Бинарная операция импликации выражается связками если..., то, из... следует, влечет. Операция записывается как                или                и задается следующей таблицей истинности:

A \rightarrow B
B
0
1
0
0
A
1
0
1
1
1
1
1
0
A \Rightarrow B
A \rightarrow B

В импликации      называется посылкой, а      — следствием. Выражение, образованное импликацией, ложно только в том случае, когда посылка истинна, а следствие ложно. При ложной посылке состояние следствия может быть каким угодно.

A
B
A \rightarrow B = !A + B

Импликация (2)

A \rightarrow B

Необходимое условие для

Достаточное условие для

A
B
B
0
1
0
0
A
1
0
1
1
1
1
1
0
A \rightarrow B

Так как      — необходимое условие для     , то не может быть такого, что достаточное условие истинно, а необходимое — ложно!

без      невозможно.

B
A
A
B

Импликация (3)

B
0
1
0
0
A
1
0
1
1
1
1
1
0
F
F = A \rightarrow B
  • Из того, что Вася — учащийся, ещё не следует, что он получает стипендию (2).
  • Но это условие необходимо, то есть если Вася не учащийся, то он заведомо не получает стипендии (1). В (3) возникает противоречие, а следовательно выражение такой импликации — ложно.

(1)

(2)

(3)

(4)

  • Если же Вася учится без троек, то он заведомо получает стипендию (4).
B := \text{Вася — учащийся}.
A := \text{Вася получает стипендию};
F := \text{суждение};

Если Вася получает стипендию, то Вася — учащийся.

Эквивалентность

Данная операция выражается связками тогда и только тогда, необходимо и до­ статочно, равносильно. Операция имеет следующие обозначения:                                             или                 . Таблица истинности выглядит так:

A == B
B
0
1
0
0
A
1
0
1
1
1
1
0
0
A \leftrightarrow B,A \Leftrightarrow B, A \equiv B
A \equiv B

Выражение, образованное эквивалентностью, истинно, если истинность обоих операндов совпадает.

A \equiv B = !A \cdot !B + A \cdot B = (!A + B) \cdot (A + !B)

Эквивалентность (2)

F_1 = A \rightarrow B
F_2 = B \rightarrow A

Если треугольник является прямоугольным, то сумма квадратов двух его сторон равна квадрату третьей стороны.

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

F_1, F_1 := \text{суждения};
A := \text{треугольник является прямоугольным};
B := \text{сумма квадратов двух сторон тр-ка равна квадрату третьей стороны}.

Штрих Шеффера

Штрих Шеффера, обычно обозначаемый         , эквивалентен операции «И-НЕ» и задаётся следующей таблицей истинности:

A | B
B
0
1
0
0
A
1
0
1
1
0
1
1
1
A | B
A | B = !(A \cdot B) = !A + !B
\&
A
B
A | B

Стрелка Пирса

Стрелка Пирса, обычно обозначаемая            , эквивалентна операции «ИЛИ-НЕ» и задаётся следующей таблицей истинности:

B
0
1
0
0
A
1
0
1
1
0
1
0
0
A \downarrow B
A \downarrow B
A \downarrow B = !(A + B) = !A \cdot !B
1
A
B
A \downarrow B

Формулы

Атомарными формулами логики высказываний называются

буквы                          с индексами и без них, а также символы истины (1) и лжи (0).

Формулами логики высказываний называются:

u, v, w, x, y, z
  • атомарные формулы;
  • выражения вида:
!(F), (F) \wedge (G), (F) \vee (G), (F) \rightarrow (G), (F) \equiv (G), (F) | (G), (F) \downarrow (G)

где     и     — формулы логики высказываний.

F
G

Примеры:

x, y, z

— формулы логики высказываний (атомарные)

(x) \rightarrow ((y) \vee (z))

— формулы логики высказываний (неатомарные)

В виду определения формулы логики высказываний приоритеты логических операций определяются скобками. 

Задачи

1) Не А
2) А, если В 

3) В случае А имеет место В

4) Как А, так и В

5) Для А необходимо В

6) Для А достаточно В

7) И A и B

 

8) А вместе с В

9) А не имеет места

10) A, только если B,

11) Или A, или B

12) A одновременно с B

13) A – то же самое, что и B

14) Коль скоро А, то В

1. Определить, какая логическая связка используется в следующих выражениях:

Задачи

а) Фрэду нравится футбол и неверно, что Фрэд любит гольф или теннис.

б) Если он выиграет в лотерею, то будет праздновать всю ночь и если он не выиграет в лотерею, то не купит компьютер.

2. Записать в символической форме высказывания и построить для них таблицы истинности:

Задачи

3. Построить таблицы истинности для следующих функций и построить комбинационную схему:

f_1(x,y,z) = !\bigl(!(x \wedge y) \vee !(x \wedge z) \vee !(y \wedge z)\bigr)
f_2(x,y,z) = \bigl ( x \wedge (x \vee y \vee z) \bigr) \vee \bigl (y \wedge (x \vee y \vee z)\bigr) \vee \bigl (z \wedge (x \vee y \vee z)\bigr)
f_3(x,y,z) = (!\bigl( (!x \wedge !y) \vee z \bigr) \rightarrow !z \vee y

* По-хорошему, сначала формулы упрощают, а потом уже работают с ними. Об упрощении формул поговорим позднее, а пока выполняем задание «в лоб».

Задачи

4. Для какого числа      истинны высказывания?

\text{1. }!\bigl((x>2) \rightarrow (x>3)\bigr)
x
\text{a)} 1;\text{ } \text{b)} 2;\text{ } \text{c)} 3;\text{ } \text{d)} 4.
\text{2. } \bigl((x<4) \rightarrow (x<3)\bigl) \wedge \bigl((x<3) \rightarrow (x<1)\bigr)
\text{a)} 1;\text{ } \text{b)} 2;\text{ } \text{c)} 3;\text{ } \text{d)} 4.
\text{3. } \bigl((x>3) \vee (x<3)\bigr) \rightarrow (x<1)
\text{a)} 1;\text{ } \text{b)} 2;\text{ } \text{c)} 3;\text{ } \text{d)} 4.

Свойства логических операций

Коммутативность

Если операция коммутативна, то результат ее применения не зависит от того, какой из операндов был первым, а какой — вторым. Операнды коммутативных операций можно менять друг с другом местами, получая тождественный результат.

x\circ y=y\circ x,\circ \in \{\land ,\lor ,\oplus ,\sim ,\mid ,\downarrow \}

Ассоциативность

Если операция ассоциативна, то результат вычисления  не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи.

(x\circ y)\circ z=x\circ (y\circ z),\circ \in \{\land ,\lor ,\oplus ,\sim \}.

Дистрибутивность

Свойство дистрибутивности одной операции относительно другой позволяет раскрывать скобки аналогично процедуре из элементарной алгебры.

x\land (y\lor z)=(x\land y)\lor (x\land z);
x\lor (y\land z)=(x\lor y)\land (x\lor z);
x\land (y\oplus z)=(x\land y)\oplus (x\land z).

Законы де Моргана

Законы де Моргана позволяют применять отрицания к целой скобке, позволяя перейти к так называемым тесным отрицаниям, когда ни одно отрицание не стоит перед скобкой.

!(x \vee y) = ! x \wedge ! y.
!(x \wedge y) = ! x \vee ! y;

Идемпотентность

Операция называется идемпотентной, если, применяя ее к двум равным операндам, получается тот же самый операнд. Идемпотентность позволяет «выкидывать» лишние повторные применения операции из формулы. Конъюнкция и дизъюнкция идемпотентны:

x \vee x = x.
x \wedge x = x;

Свойства единицы и нуля

Конъюнкция и дизъюнкция «по-особому» реагируют на единицу или ноль в качестве одного из операндов независимо от значения второго. Эти свойства похожи на знакомые из элементарной алгебры умножение на единицу, умножение на ноль, сложение с нулём:

x \vee 0 = x, x \vee 1 = 1.
x \wedge 0 = 0, x \wedge 1 = x;

Законы поглощения

Если к выражению применяется с одним и тем же операндом сначала одна операция, а потом, с тем же самым операндом, поглощающая её, то значение выражения поглощается,
становясь равно операнду. Таким образом поглощающие друг друга пары операций можно «выкидывать»
во время упрощения.

x\land (x\lor y)=x;
x\lor (x\land y)=x.

Дополнение

Отрицание операнда называется его дополнением. Конъюнкция или дизъюнкция операнда со своим дополнением даёт однозначные результат независимо от значения операнда:

x \wedge ! x = 0;
x \vee ! x = 1.

Двойное отрицание

Двойное отрицание компенсирует само себя. Таким образом в форме с тесными отрицаниями у каждой переменной в выражении либо не стоит ни одного отрицания, либо только одно.

!!x = x.

Тождественно истинная формула

Формула     называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных

F
0
\vdots
0
x_1
0
0
x_2
...
x_n
F(x_1, ..., x_n)
0...0
0
0...0
1
\vdots
\vdots
\vdots
\vdots
1...1
1...1
0
1
1
1
1
1
1
1
1
1

везде истина

Тождественно ложная формула

Формула     называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных

F
0
\vdots
0
x_1
0
0
x_2
...
x_n
F(x_1, ..., x_n)
0...0
0
0...0
1
\vdots
\vdots
\vdots
\vdots
1...1
1...1
0
1
1
1
1
1
0
0
0
0

везде ложь

Равносильность формул

Две формулы алгебры логики     и     называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).

F
G
F \equiv G

 * если формулы      и      равносильны, то формула              тавтология, и обратно, если формула             тавтология, то формулы     и   равносильны.

F
G
F \equiv G
F \equiv G
F
G

Задачи

1. Упростить логические выражения:

b) \text{ } \bigl((x \vee y) \wedge !x \bigr) \vee \bigl(!(x \vee y) \wedge !!x \bigr);
a)\text{ } (x \wedge y) \vee (x \wedge !y \wedge z) \vee (!y \wedge x \wedge !z) \vee (x \wedge !z);
c) \text{ }!\bigl((x \wedge y) \vee (!x \wedge !y) \bigr) \wedge (x \vee !y);
d) \text{ } (x \vee y \vee z) \wedge (x \vee !y \vee !z);
e) \text{ } \Bigl[ !x \vee \bigl[ (y \rightarrow !x) \Leftrightarrow \bigl(!(x \wedge !y) \vee x\bigr)\bigr]\Bigr] \wedge \bigl[(!x \wedge y) \Leftrightarrow (!y \rightarrow x) \bigr].

Задачи

2. Доказать равносильность формул:

a) \text{ } !\bigl[ (x \vee y) \wedge (x \wedge !z) \bigr] \text{ и } x \rightarrow z
b) \text{ } !\bigl[ (x \vee !y) \wedge y \bigr] \wedge !\bigl[!x \wedge y \bigr] \text{ и } !y
c) \text{ } (x \wedge y) \vee (!x \wedge y) \vee (x \wedge !y) \text{ и } x \vee y
d) \text{ } !\bigl[ (x \wedge y) \vee !z \bigr ] \text{ и } !(z \rightarrow x) \vee !(y \leftarrow z)

Дизъюнктивная нормальная форма (ДНФ)

Дизъюнктивная нормальная форма (ДНФ) — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.

x\lor y

Примеры:

(x\land y\land ! z)\lor (!u\land w\land v)\lor (z\land u)\lor y
!(x \vee y)
x \lor (y\land (z \lor x))

Данные выражения не находятся в ДНФ, но приводимы к ней

Совершенная дизъюнктивная нормальная форма (СДНФ)

Совершенной дизъюктивной нормальной формой (СДНФ) называется такая ДНФ, у которой в каждую простую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.

y
0
1
0
0
x
1
0
1
1
1
0
1
0
f(x; y)
\Rightarrow x \wedge y
\Rightarrow !x \wedge y
\Rightarrow f(x;y) = (!x \wedge y)\vee (x \wedge y)

Конъюктивная нормальная форма (КНФ)

Конъюнктивная нормальная форма (КНФ) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

(x\vee y)\wedge (y\vee z)
x\wedge (y\vee z)\wedge (y\vee u)

Примеры:

!x\wedge (y\vee z)
(x\vee y)\wedge (! y\vee z\vee !u)\wedge (u\vee !w)

Данные выражения не находятся в КНФ, но приводимы к ней

x\wedge y

Совершенная конъюктивная нормальная форма (СКНФ)

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.

y
0
1
0
0
x
1
0
1
1
1
0
1
0
f(x; y)
\Rightarrow !x \vee y
\Rightarrow x \vee y
\Rightarrow f(x;y) = (x \vee y)\wedge (!x \vee y)

Задачи

Формализовать (описать) алгоритм работы цифрового устройства на языке функций алгебры логики и построить соответствующую комбинационную схему (схема должна отличаться минимумом аппаратных затрат):

 

1. Программа экзаменатор даёт сигнал «зачёт» (загорается табло) в том и только в том случае, если экзаменующийся ответил правильно не менее чем на три вопроса из четырёх.

 

2. Программа экзаменатор даёт сигнал «зачёт» (загорается табло) в том и только в том случае, если экзаменующийся ответил правильно на первый вопрос и не менее чем на два вопроса из четырёх, содержащихся в билете.

Задачи

Формализовать (описать) алгоритм работы цифрового устройства на языке функций алгебры логики и построить соответствующую комбинационную схему (схема должна отличаться минимумом аппаратных затрат):

 

3. На летательном аппарате (ЛА) должно загораться табло «Посадка возможна» при выполнении следующих условий: при посадке ЛА закрылки должны быть в положении 3 или 4 (из четырёх возможных положений закрылок), кроме того при посадке ЛА должны быть выпущены шасси и убраны предкрылки.

 

Логические уравнения и системы логических уравнений

Что такое уравнение?

Уравнение — математическое равенство с одной или несколькими неизвестными величинами. 

Уравнение. Определение

Что значит решить уравнение?

Решить уравнение — значит найти все его корни или убедиться, что их нет.

Решить уравнение. Определение

Примеры логических уравнений

(x_1 \rightarrow x_2) \cdot \text{} !(x_2 \rightarrow x_3) \cdot (x_3 \rightarrow x_4) = 0,
x_1, x_2, x_3, x_4

где                              — логические переменные.

(x + y) \rightarrow (y \Leftrightarrow z) = 1,

где                — логические переменные.

x, y, z
[!(x + y)\cdot z] \rightarrow [(!z \cdot !x) + u] = 0,

где                     — логические переменные.

x, y, z, u

и т.п. ...

Ещё вопросик...

(x_1 \rightarrow x_2) \cdot \text{} !(x_2 \rightarrow x_3) \cdot (x_3 \rightarrow x_4) = 1

Является ли преобразование равносильным (относительно математической логики)?

\Leftrightarrow
\begin{cases} (x_1 \rightarrow x_2) = 1;\\ !(x_2 \rightarrow x_3) = 1;\\ (x_3 \rightarrow x_4) = 1. \end{cases}

А если так?

(x_1 \rightarrow x_2) \cdot \text{} !(x_2 \rightarrow x_3) \cdot (x_3 \rightarrow x_4) = 0

Является ли преобразование равносильным (относительно математической логики)?

\Leftrightarrow
\begin{cases} (x_1 \rightarrow x_2) = 0;\\ !(x_2 \rightarrow x_3) = 0;\\ (x_3 \rightarrow x_4) = 0. \end{cases}

А теперь... что такое система уравнений?

Система уравнений. Определение

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Преобразования ур-й в системы

f \cdot g = 1 \Leftrightarrow \begin{cases} f = 1;\\ g = 1.\\ \end{cases}
f + g = 1 \Leftrightarrow \left[ \begin{array}{l} \begin{cases} f = 1;\\ g = 1;\\ \end{cases}\\ \begin{cases} f = 0;\\ g = 1;\\ \end{cases}\\ \begin{cases} f = 1;\\ g = 0.\\ \end{cases}\\ \end{array} \right.
f \cdot g = 0 \Leftrightarrow \left[ \begin{array}{l} \begin{cases} f = 0;\\ g = 0;\\ \end{cases}\\ \begin{cases} f = 0;\\ g = 1;\\ \end{cases}\\ \begin{cases} f = 1;\\ g = 0.\\ \end{cases}\\ \end{array} \right.
f + g = 0 \Leftrightarrow \begin{cases} f = 0;\\ g = 0.\\ \end{cases}

Решить уравнение (1)

[!(x + y)z] \rightarrow [!z!x + u] = 0.

Решение

[!(x + y)z] \rightarrow [!z!x + u] = 0;

I способ (через упрощения):

II способ (методом логических рассуждений):

(!x!yz) \rightarrow (!z!x + u) = 0;
!(!x!yz) + (!z!x + u) = 0;
x + y + !z + !z!x + u = 0;
x + y + !z + u = 0;
\begin{cases} x = 0;\\ y = 0;\\ !z = 0;\\ u = 0; \end{cases} \Leftrightarrow \begin{cases} x = 0;\\ y = 0;\\ z = 1;\\ u = 0. \end{cases}
[!(x + y)z] \rightarrow [!z!x + u] = 0;
1
0
\begin{cases} !x!yz = 1;\\ !z!x + u = 0;\\ \end{cases} \Leftrightarrow \begin{cases} \begin{cases} x = 0;\\ y = 0;\\ z = 1;\\ \end{cases}\\ \begin{cases} z = 1;\\ u = 0; \end{cases}\\ \end{cases} \Leftrightarrow \begin{cases} x = 0;\\ y = 0;\\ z = 1;\\ u = 0. \end{cases}

Ответ:

x = 0; y = 0; z = 1; u = 0.

Решение (нерациональный способ)

f = [!(x + y)z] \rightarrow [!z!x + u]

III способ (через таблицы истинности):

Ответ:

x = 0; y = 0; z = 1; u = 0.
f = 0

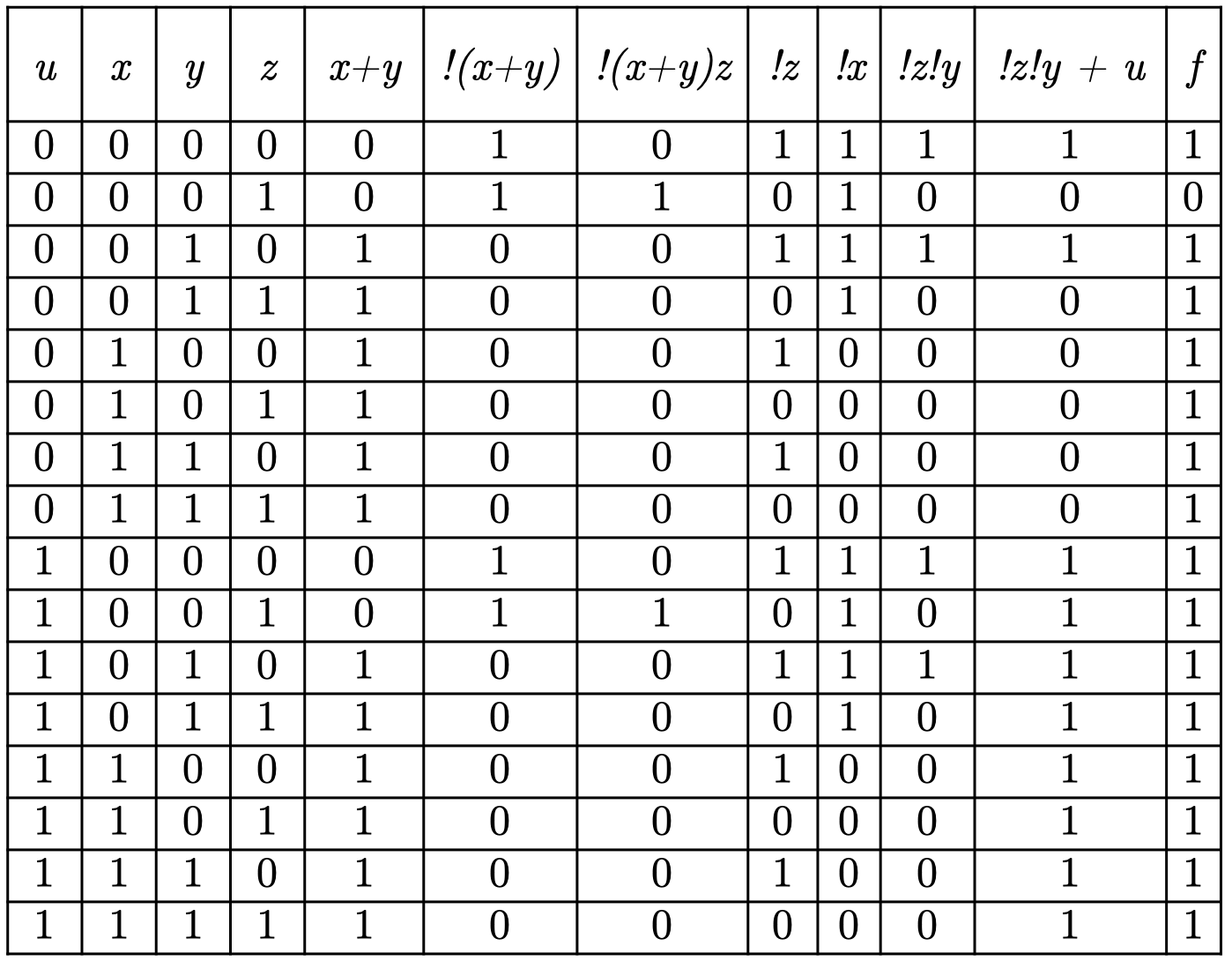
, что и требовалось найти

Решить уравнение (2)

(x \rightarrow y)(x \rightarrow !y)(!x \rightarrow y!zu) = 1.
(x \rightarrow y)(x \rightarrow !y)(!x \rightarrow y!zu) = 1.
(!x + y)(!x + !y)(!!x + y!zu) = 1;
(!x!x + !x!y + y!x + y!y)(x + y!zu) = 1;
(!x + !x!y + y!x)(x + y!zu) = 1;
!x(x + y!zu) = 1;
!xx + !xy!zu = 1;
\begin{cases} !x = 1;\\ y = 1;\\ !z = 1;\\ u = 1; \end{cases} \Leftrightarrow \begin{cases} x = 0;\\ y = 1;\\ z = 0;\\ u = 1. \end{cases}
!xy!zu = 1;

Решение (через упрощение)

x = 0; y = 1; z = 0; u = 1.

Ответ:

(x \rightarrow y)(x \rightarrow !y)(!x \rightarrow y!zu) = 1.

Решение (мтд. лог. рассуждений)

x = 0; y = 1; z = 0; u = 1.

Ответ:

1
1
1
\begin{cases} x \rightarrow y = 1; (1)\\ x \rightarrow !y = 1; (2)\\ !x \rightarrow y!zu = 1; (3)\\ \end{cases} % \Leftrightarrow % \begin{cases} % \begin{cases} % x = 0;\\ % y = 0;\\ % z = 1;\\ % \end{cases}\\ % \begin{cases} % z = 1;\\ % u = 0; % \end{cases}\\ % \end{cases} % \Leftrightarrow % \begin{cases} % x = 0;\\ % y = 0;\\ % z = 1;\\ % u = 0. % \end{cases}
\begin{cases} x = 0;\\ y = \left[ \begin{array}{l} 0;\\ 1.\\ \end{array} \right. \end{cases}

Из уравнения (1) и (2) логично положить следующее:

Теперь видно, что уравнение (3) несёт в себе импликацию           . Следовательно, осталось только решить уравнение               , откуда видно, что

1 \rightarrow 1
y!zu = 1
y = 1; z = 0; u = 1.

Сколько различных решений имеет уравнение?

(x + y)(z + u) = 1.

Решение

(x + y)(z + u) = 1.
1
1
{\underbrace{\text{\hspace{0.8cm}}}}
{\underbrace{\text{\hspace{0.8cm}}}}
3
3
\Sigma = 3 \cdot 3 = 9.

Ответ: 9.

Способ I (прямым ходом):

Способ II (от противного):

(x + y)(z + u) = 0.
f_1 = \left[ \begin{array}{l} 0;\\ 1. \end{array} \right.
f_2 = \left[ \begin{array}{l} 0;\\ 1. \end{array} \right.
\overline{Eq} \Leftrightarrow \left[ \begin{array}{l} \begin{cases} f_1 = 0;\\ f_2 = 0;\\ \end{cases}\\ \begin{cases} f_1 = 0;\\ f_2 = 1;\\ \end{cases}\\ \begin{cases} f_1 = 1;\\ f_2 = 0.\\ \end{cases}\\ \end{array} \right.
1 \cdot 1
1 \cdot 3
3 \cdot 1
\overline{\Sigma} = 1 + 3 + 3 = 7.
\Sigma = 16 - 7 = 9.

*когда выражение равно нулю

**видно из таблиц истинности слева

a) \text{ } (xy + z) \rightarrow (z + p) = 0;

Задачи

b) \text{ } x(y \rightarrow z)(y \rightarrow x) + y = 0;

Методы решений систем логических уравнений

Метод полного перебора (метод «грубой силы»)

\begin{cases} (x_1 \rightarrow x_2) = 1;\\ (y_1 \rightarrow y_2) = 1;\\ (x_1 \rightarrow y_1) = 1; \end{cases}
(x_1 \rightarrow x_2)(y_1 \rightarrow y_2) (x_1 \rightarrow y_1) = 1;
\Leftrightarrow
\left[ \begin{array}{l} x_1=0; x_2=0; y_1 = 0; y_2 = 0;\\ x_1=0; x_2=0; y_1 = 0; y_2 = 1;\\ x_1=0; x_2=0; y_1 = 1; y_2 = 1;\\ x_1=0; x_2=1; y_1 = 0; y_2 = 0;\\ x_1=0; x_2=1; y_1 = 0; y_2 = 1;\\ x_1=0; x_2=1; y_1 = 1; y_2 = 1;\\ x_1=1; x_2=1; y_1 = 1; y_2 = 1;\\ \end{array} \right.

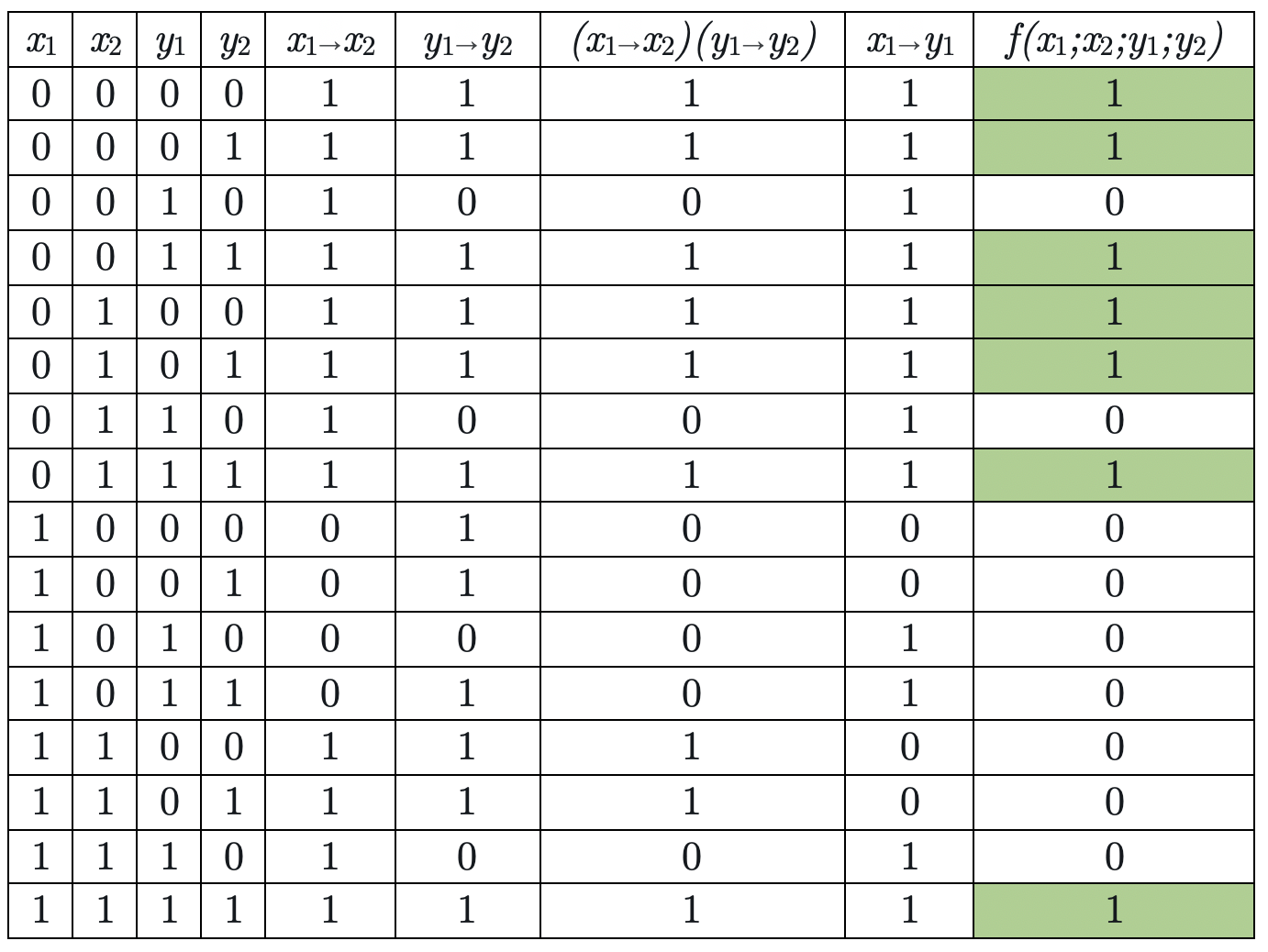
Метод полного перебора (метод «грубой силы») (2)

\begin{cases} (x_1 \rightarrow x_2) = 1;\\ (y_1 \rightarrow y_2) = 1;\\ (x_1 \rightarrow y_1) = 1; \end{cases} \Leftrightarrow (x_1 \rightarrow x_2)(y_1 \rightarrow y_2) (x_1 \rightarrow y_1) = 1 \Leftrightarrow
\Leftrightarrow (!x_1 + x_2)(!y_1 + y_2) (!x_1 + y_1) = 1.
# Python:
for x1 in [0,1]:
  for x2 in [0,1]:
    for y1 in [0,1]: 
      for y2 in [0,1]:
        if (not(x1) or x2) and (not(y1) or y2) and (not(x1) or y1):
          print('x1 = {}; x2 = {}; y1 = {}; y2 ={}'.format(x1, x2, y1, y2))

-- Haskell:
f :: [(Bool, Bool, Bool, Bool)]
f = filter predicat [(x1,x2,y1,y2) | x1 <- bs, x2 <- bs, y1 <- bs, y2 <- bs]
  where
    predicat (x1,x2,y1,y2) = (not x1 || x2) && (not y1 || y2) && (not x1 || y1) == True
    bs                     = [False,True]

Метод замены переменных

\begin{cases} \bigl((x_1 \Leftrightarrow x_2) + (x_3 \Leftrightarrow x_4)\bigr) \wedge \bigl(!(x_1 \Leftrightarrow x_2) + !(x_3 \Leftrightarrow x_4)\bigr) = 1;\\ \bigl((x_3 \Leftrightarrow x_4) + (x_5 \Leftrightarrow x_6)\bigr) \wedge \bigl(!(x_3 \Leftrightarrow x_4) + !(x_5 \Leftrightarrow x_6)\bigr) = 1;\\ \bigl((x_5 \Leftrightarrow x_6) + (x_7 \Leftrightarrow x_8)\bigr) \wedge \bigl(!(x_5 \Leftrightarrow x_6) + !(x_7 \Leftrightarrow x_8)\bigr) = 1;\\ \bigl((x_7 \Leftrightarrow x_8) + (x_9 \Leftrightarrow x_{10})\bigr) \wedge \bigl(!(x_7 \Leftrightarrow x_8) + !(x_9 \Leftrightarrow x_{10})\bigr) = 1. \end{cases}
\Bigl|_{ \small{ \left. \begin{array}{l} t_1 = (x_1 \Leftrightarrow x_2)\\ t_2 = (x_3 \Leftrightarrow x_4)\\ t_3 = (x_5 \Leftrightarrow x_6)\\ t_4 = (x_7 \Leftrightarrow x_8)\\ t_5 = (x_9 \Leftrightarrow x_{10}) \end{array} \right. }} \Rightarrow \begin{cases} (t_1 + t_2) \wedge (!t_1 + !t_2) = 1;\\ (t_2 + t_3) \wedge (!t_2 + !t_3) = 1;\\ (t_3 + t_4) \wedge (!t_3 + !t_4) = 1;\\ (t_4 + t_5) \wedge (!t_4 + !t_5) = 1;\\ \end{cases} \Leftrightarrow \begin{cases} t_1 \oplus t_2 = 1;\\ t_2 \oplus t_3 = 1;\\ t_3 \oplus t_4 = 1;\\ t_4 \oplus t_5 = 1; \end{cases}

Применяется, если можно выделить одинаковые выражения в уравнениях, между которыми нет общих переменных:

\Rightarrow \left[ \begin{array}{l} t_1=0; t_2=1; t_3 = 0; t_4 = 1; t_5 = 0;\\ t_1=1; t_2=0; t_3 = 1; t_4 = 0; t_5 = 1.\\ \end{array} \right.

Метод замены переменных (2)

Обратная замена:

\begin{cases} \begin{cases} t_1 = (x_1 \Leftrightarrow x_2);\\ t_2 = (x_3 \Leftrightarrow x_4);\\ t_3 = (x_5 \Leftrightarrow x_6);\\ t_4 = (x_7 \Leftrightarrow x_8);\\ t_5 = (x_9 \Leftrightarrow x_{10});\\ \end{cases} \\ \left[ \begin{array}{l} t_1=0; t_2=1; t_3 = 0; t_4 = 1; t_5 = 0;\\ t_1=1; t_2=0; t_3 = 1; t_4 = 0; t_5 = 1.\\ \end{array} \right. \end{cases} \Rightarrow \left[ \begin{array}{l} \begin{cases} 0 = (x_1 \Leftrightarrow x_2);\\ 1 = (x_3 \Leftrightarrow x_4);\\ 0 = (x_5 \Leftrightarrow x_6);\\ 1 = (x_7 \Leftrightarrow x_8);\\ 0 = (x_9 \Leftrightarrow x_{10}); \end{cases} \\ \begin{cases} 1 = (x_1 \Leftrightarrow x_2);\\ 0 = (x_3 \Leftrightarrow x_4);\\ 1 = (x_5 \Leftrightarrow x_6);\\ 0 = (x_7 \Leftrightarrow x_8);\\ 1 = (x_9 \Leftrightarrow x_{10}). \end{cases} \end{array} \right.

Комбинаторика в помощь!

\Rightarrow \sum_{(1)} = 2^5 = 32.
\sum_{(2)} = 2^5 = 32.

По два решения на каждое уравнение

Аналогично и для второй системы:

\sum = \sum_{(1)} + \sum_{(2)} = 32 + 32 = 64.

Таким образом, всего решений данной системы:

Ответ: 64.

Задачи

Найти количество решений систем уравнений методом замены переменных:

\begin{cases} (x_1 \cdot y_1) \Leftrightarrow (!x_2 + !y_2) = 1;\\ (x_2 \cdot y_2) \Leftrightarrow (!x_3 + !y_3) = 1;\\ (x_3 \cdot y_3) \Leftrightarrow (!x_4 + !y_4) = 1;\\ ...\\ (x_6 \cdot y_6) \Leftrightarrow (!x_7 + !y_7) = 1.\\ \end{cases}

Метод динамического программирования (метод отображения)

\begin{cases} (x_1 \Leftrightarrow x_2) \rightarrow (x_3 + x_4) = 1;\\ (x_3 \Leftrightarrow x_4) \rightarrow (x_5 + x_6) = 1;\\ (x_5 \Leftrightarrow x_6) \rightarrow (x_7 + x_8) = 1.\\ \end{cases}

Используется, когда в системе имеются «влияющие группы» переменных на другие группы.

Имеется некоторая зависимость:            влияют на           ,           , в свою очередь на

и так далее. Выявим закономерность получения пар значений:

x_1, x_2
x_3, x_4
x_3, x_4
x_5, x_6
00 (1)
01 (1)
10 (1)
11 (1)
00 (1 + 1 = 2)
01 (1 + 1 + 1 + 1 = 4)
10 (1 + 1 + 1 + 1 = 4)
11 (1 + 1 + 1 + 1= 4)
x_1x_2
x_3x_4
00 (4 + 4 = 8)
01 (2 + 4 + 4 + 4 = 14)
10 (2 + 4 + 4 + 4 = 14)
11 (2 + 4 + 4 + 4 = 14)
x_5x_6
00 (14 + 14 = 28)
01 (8 + 14 + 14 + 14 = 50)
10 (8 + 14 + 14 + 14 = 50)
11 (8 + 14 + 14 + 14 = 50)
x_7x_8
\sum_{(1)} = 2 + 4 + 4 + 4 = 14
\sum_{(2)} = 8 + 14 + 14 + 14 = 50
\sum_{(3)} = 28 + 50 + 50 + 50 = 178

Ответ

Задачи

\begin{cases} (x_1 + x_2) \rightarrow (x_3\cdot x_4) = 1;\\ (x_3 + x_4) \rightarrow (x_5\cdot x_6) = 1;\\ (x_5 + x_6) \rightarrow (x_7\cdot x_8) = 1.\\ \end{cases}

Найти количество решений систем уравнений методом динамического программирования:

\begin{cases} (x_1 \cdot y_1) \Leftrightarrow (!x_2 + !y_2) = 1;\\ (x_2 \cdot y_2) \Leftrightarrow (!x_3 + !y_3) = 1;\\ (x_3 \cdot y_3) \Leftrightarrow (!x_4 + !y_4) = 1;\\ ...\\ (x_6 \cdot y_6) \Leftrightarrow (!x_7 + !y_7) = 1.\\ \end{cases}
\begin{cases} (x_1 \rightarrow x_2) \wedge (y_1 \rightarrow y_2) = 1;\\ (x_2 \rightarrow x_3) \wedge (y_2 \rightarrow y_3) = 1;\\ ...\\ (x_9 \rightarrow x_{10}) \wedge (y_9 \rightarrow y_{10}) = 1. \end{cases}
\begin{cases} (x_1 \Leftrightarrow x_2) \Leftrightarrow (y_1 \Leftrightarrow y_2) = 1;\\ (x_2 \Leftrightarrow x_3) \Leftrightarrow (y_2 \Leftrightarrow y_3) = 1;\\ ...\\ (x_6 \Leftrightarrow x_7) \Leftrightarrow (y_6 \Leftrightarrow y_7) = 1. \end{cases}
\begin{cases} (x_1 \Leftrightarrow x_2) \rightarrow (x_2 \Leftrightarrow x_3) = 1;\\ (x_2 \Leftrightarrow x_3) \rightarrow (x_3 \Leftrightarrow x_4) = 1;\\ ...\\ (x_7 \Leftrightarrow x_8) \rightarrow (x_8 \Leftrightarrow x_9) = 1. \end{cases}
\begin{cases} \bigl[(x_1 \Leftrightarrow x_2) \rightarrow (x_2 \Leftrightarrow x_3) \bigr] \bigl[(y_1 \Leftrightarrow y_2) \rightarrow (y_2 \Leftrightarrow y_3) \bigr] = 1;\\ \bigl[(x_2 \Leftrightarrow x_3) \rightarrow (x_3 \Leftrightarrow x_4) \bigr] \bigl[(y_2 \Leftrightarrow y_3) \rightarrow (y_3 \Leftrightarrow y_4) \bigr] = 1;\\ ...\\ \bigl[(x_6 \Leftrightarrow x_7) \rightarrow (x_7 \Leftrightarrow x_8) \bigr] \bigl[(y_6 \Leftrightarrow y_7) \rightarrow (y_7 \Leftrightarrow y_8) \bigr] = 1; \end{cases}

а)

б)

в)

г)

д)

е)

Метод построения дерева решений

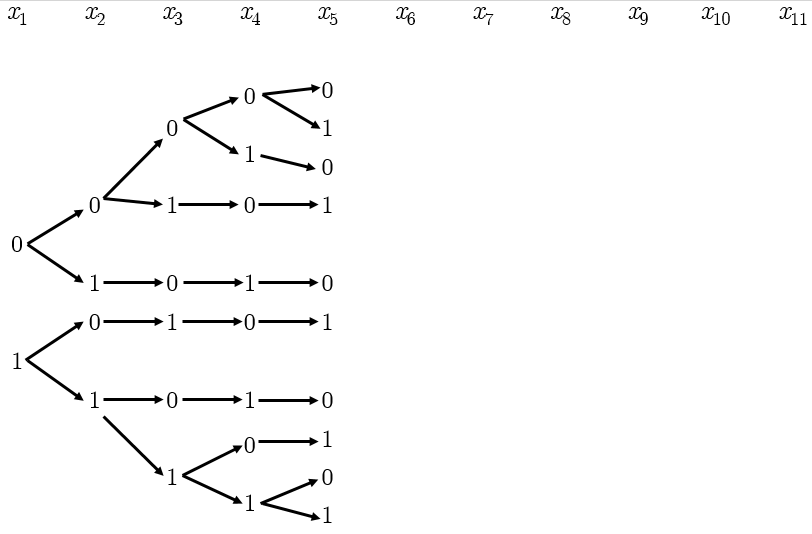
\begin{cases} !(x_1 \Leftrightarrow x_2)\cdot \bigl[(x_1 \cdot !x_3) + (!x_1 \cdot x_3)\bigr] = 0;\\ !(x_2 \Leftrightarrow x_3)\cdot \bigl[(x_2 \cdot !x_4) + (!x_2 \cdot x_4)\bigr] = 0;\\ !(x_3 \Leftrightarrow x_4)\cdot \bigl[(x_3 \cdot !x_5) + (!x_3 \cdot x_5)\bigr] = 0;\\ ...\\ !(x_9 \Leftrightarrow x_{10})\cdot \bigl[(x_9 \cdot !x_{11}) + (!x_9 \cdot x_{11})\bigr] = 0; \end{cases}

2       4      6      8     10     12     14    16   18    20    22    

\sum:
\Delta = 2
\begin{cases} \\\\ \end{cases}

...

Ответ: 22.

Задачи

\begin{cases} (x_1 \Leftrightarrow x_2) \rightarrow (x_2 \Leftrightarrow x_3) = 1;\\ (x_2 \Leftrightarrow x_3) \rightarrow (x_3 \Leftrightarrow x_4) = 1;\\ ...\\ (x_6 \Leftrightarrow x_7) \rightarrow (x_7 \Leftrightarrow x_8) = 1.\\ \end{cases}

Найти количество решений систем уравнений методом построения дерева решений:

Табличный метод

\begin{cases} (x_1 \rightarrow x_2)(x_2 \rightarrow x_3)(x_3 \rightarrow x_4) = 1; \text{ } (1)\\ (y_1 \rightarrow y_2)(y_2 \rightarrow y_3)(y_3 \rightarrow y_4) = 1; \text{ } (2)\\ (z_1 \rightarrow z_2)(z_2 \rightarrow z_3)(z_3 \rightarrow z_4) = 1. \text{ } (3) \end{cases}
0 0 0 0
0 0 0 1
0 0 1 1
0 1 1 1
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 1
0 1 1 1
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 1
0 1 1 1
1 1 1 1
x_1
x_2
x_3
x_4
y_1
y_2
y_3
y_4
z_1
z_2
z_3
z_4

5 вариантов

на каждый вариант ещё по 5 вариантов

то есть

5 \cdot 5 = 25

25

25

25

25

25

\sum = 25 \cdot 5 = 125

Ответ: 125.

\begin{cases} (x_1 \rightarrow x_2) \wedge (y_1 \rightarrow y_2) = 1;\\ (x_2 \rightarrow x_3) \wedge (y_2 \rightarrow y_3) = 1;\\ (x_4 \rightarrow x_{5}) \wedge (y_4 \rightarrow y_{5}) = 1;\\ x_1 + y_1 = 1. \end{cases}

Задачи

Найти количество решений систем уравнений:

\begin{cases} (x_1 \vee \neg x_2) \wedge (x_2 \vee \neg x_3) \wedge (x_3 \vee \neg x_4) \wedge (x_4 \vee \neg x_5) = 1;\\ (\neg y_1 \vee y_2) \wedge (\neg y_2 \vee y_3) \wedge (\neg y_3 \vee y_4) \wedge (\neg y_4 \vee y_5) = 1;\\ (x_1 \vee y_1) = 1. \end{cases}
\begin{cases} (x_1 \rightarrow x_2)(x_2 \rightarrow x_3)(x_3 \rightarrow x_4)(x_4 \rightarrow x_5)(x_6 \rightarrow x_6) = 1;\\ (y_1 \rightarrow y_2)(y_2 \rightarrow y_3)(y_3 \rightarrow y_4)(y_4 \rightarrow y_5)(y_6 \rightarrow y_6) = 1;\\ (z_1 \rightarrow z_2)(z_2 \rightarrow z_3)(z_3 \rightarrow z_4)(z_4 \rightarrow z_5)(z_6 \rightarrow z_6) = 1;\\ x_1 + y_1 + z_1 = 1. \end{cases}

а)

б)

в)

Логические уравнения с параметрами

Пример I-1

\bigl( (x \le 9) \rightarrow (x^2 \le A) \bigr) \wedge \bigl( (y^2 \le A) \rightarrow (y \le 9) \bigr)

Для какого наибольшего целого числа      формула ниже тождественно истинна, т.е. принимает значение 1 при любых целых и неотрицательных      и     ?

x
y
A

Решение:

Шаг I. Упрощаем и приводим к виду системы:

\bigl( (x > 9) \vee (x^2 \le A) \bigr) \wedge \bigl( (y^2 > A) \vee (y \le 9) \bigr)
\begin{cases} \left[ \begin{array}{l} x > 9; (1)\\ x^2 \le A; (2) \end{array} \right. \\ \left[ \begin{array}{l} y^2 > A; (3)\\ y \le 9; (4) \end{array} \right. \end{cases}
\Leftrightarrow

При выполнении условий (1) и (4) формула тождественно истинна

Шаг II. Рассматриваем случаи, отличные от истинных условий (1) и (4):

\begin{cases} \begin{cases} x \le 9; \\ x^2 \le A ; \end{cases} \\ \begin{cases} y^2 > A; \\ y > 9; \end{cases} \end{cases} \Rightarrow \begin{cases} \begin{cases} x \le 9; \\ x^2 \le A ; \end{cases} \\ \begin{cases} y^2 > A; \\ y \ge 10; \end{cases} \end{cases} \Rightarrow \begin{cases} 9^2 \le A; \\ 10^2 > A; \end{cases} \Rightarrow 81 \le A < 100 \Rightarrow A_{\max} = 99.

Ответ: 99.

y \in \Z_+

*условие с параметром не трогаем!

Пример I-2

\bigl( (x < 6) \rightarrow (x^2 < A) \bigr) \wedge \bigl( (y^2 \le A) \rightarrow (y \le 6) \bigr)

Сколько существует целых значений      , при которых формула ниже тождественно истинна, т.е. принимает значение 1 при любых целых и неотрицательных      и     ?

x
y
A

Решение:

Шаг I. Упрощаем и приводим к виду системы:

\bigl( (x \ge 6) \vee (x^2 < A) \bigr) \wedge \bigl( (y^2 > A) \vee (y \le 6) \bigr)
\begin{cases} \left[ \begin{array}{l} x \ge 6; (1)\\ x^2 < A; (2) \end{array} \right. \\ \left[ \begin{array}{l} y^2 > A; (3)\\ y \le 6; (4) \end{array} \right. \end{cases}
\Leftrightarrow

При выполнении условий (1) и (4) формула тождественно истинна

Шаг II. Рассматриваем случаи, отличные от истинных условий (1) и (4):

\begin{cases} \begin{cases} x < 6; \\ x^2 < A ; \end{cases} \\ \begin{cases} y^2 > A; \\ y > 6; \end{cases} \end{cases} \Rightarrow \begin{cases} \begin{cases} x \le 5; \\ x^2 < A ; \end{cases} \\ \begin{cases} y^2 > A; \\ y \ge 7; \end{cases} \end{cases} \Rightarrow \begin{cases} 5^2 < A; \\ 7^2 > A; \end{cases} \Rightarrow 25 < A < 49 \Rightarrow |A| = 23.

Ответ: 23.

x \in \Z_+
y \in \Z_+

*условие с параметром не трогаем!

Пример I-3

\bigl( (x \in A) \rightarrow (x^2 \le 81) \bigr) \wedge \bigl( (y^2 \le 36) \rightarrow (y \in A) \bigr)

На числовой прямой задан отрезок     . Известно, что формула, описанная ниже, тождественно истинна при любых вещественных     и    . Какую наибольшую длину может иметь отрезок     ?

x
y
A

Решение:

Шаг I. Упрощаем и приводим к виду системы:

\bigl( (x \notin A) \vee (x^2 \le 81) \bigr) \wedge \bigl( (y^2 > 36) \vee (y \in A) \bigr)
\begin{cases} \left[ \begin{array}{l} x \notin A;\\ x^2 \le 81; \end{array} \right. \\ \left[ \begin{array}{l} y^2 > 36; \\ y \in A; \end{array} \right. \end{cases} \Leftrightarrow \begin{cases} \left[ \begin{array}{l} x \notin A; (1)\\ x \in [-9; 9]; (2) \end{array} \right. \\ \left[ \begin{array}{l} y \in (-\infty; -6) \cup (6; +\infty); (3)\\ y \in A; (4) \end{array} \right. \end{cases}
\Leftrightarrow

Шаг II. Рассматриваем случаи, отличные от истинных условий (2) и (3):

Ответ: 18.

A
-9
9
-6
6
x
y
\begin{cases} \\ \\ \end{cases}
\underbrace{\text{\hspace{0.9cm}}}
\underbrace{\text{\hspace{0.7cm}}}
\underbrace{\text{\hspace{0.7cm}}}
A
!A
!A
A \in [-9; 9]
|A| = 18.
\Rightarrow

Пример II-1

F(x) = \bigl( (x \in P) \Leftrightarrow (x \in Q)\bigr) \rightarrow !(x \in A)

На числовой прямой даны два отрезка:                     и                       . Указать наибольшую возможную длину промежутка     , для которого формула

x
A
P = [5, 30]
Q = [14, 23]

тождественно истинна, при любом значении переменной    .

Шаг I. Упрощаем:

F = !\bigl( (x \in P) \Leftrightarrow (x \in Q)\bigr) \vee (x \notin A)
x
5
14
23
30
P
Q
\underbrace{\text{\hspace{1.77cm}}}
!\bigl( (x \in P) \Leftrightarrow (x \in Q)\bigr) = 0
[14;23]
\underbrace{\text{\hspace{0.9cm}}}
\underbrace{\text{\hspace{0.3cm}}}
(- \infty;5)
(30;+\infty)
x \notin A .

Для истинности       необходимо 

F

Для всех остальных неважно наличие условия           

x \in A

Но ищется наибольшая возможная длина    , следовательно выбираем наибольший промежуток больше из оставшихся

A
\underbrace{\text{\hspace{1.7cm}}}
\underbrace{\text{\hspace{1.45cm}}}
\mathrm{card}(A_1) = \bigl|[5;14)\bigr| = 9
\mathrm{card}(A_2) = \bigl|(23;30]\bigr| = 7

Ответ: 9.

*обозначение мощности множ-ва, аналогично записи

|A_1|

Шаг II. Рассматриваем формулу графически:

Решение:

Пример II-2

\bigl((x \in A ) \rightarrow (x \in P)\bigr) \wedge \bigl((x \in Q) \rightarrow !(x \in A)) = 1.

Элементами множеств                являются натуральные числа, причём

 

Определить наибольшее возможное количество элементов в множестве  , таких, чтобы следующее выражение было истинным при любом значении   .

 

A, P, Q
Q = \{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\}.
P = \{2, 4, 6, 8, 10, 12, 14, 16, 18, 20\},
A

Шаг I. Упрощаем (предварительно заменив условия (для краткости записи):

Пусть                                                       , тогда:

Для наглядности выполним обратную замену:

(a \rightarrow p) \cdot (q \rightarrow !a) \Leftrightarrow (!a + p) \cdot (!q + !a) \Leftrightarrow !a + (p \cdot !q).
x \in A \equiv a, x \in P \equiv p, x \in Q \equiv q
(x \notin A) \vee \bigl((x \in P) \wedge (x \notin Q)\bigr).

Шаг II. Рассматриваем элементы множества в совокупности с выражением:

(x \in P) \wedge (x \notin Q) = 0
x \notin A .

Для истинности  выр-я необходимо наличие усл-я

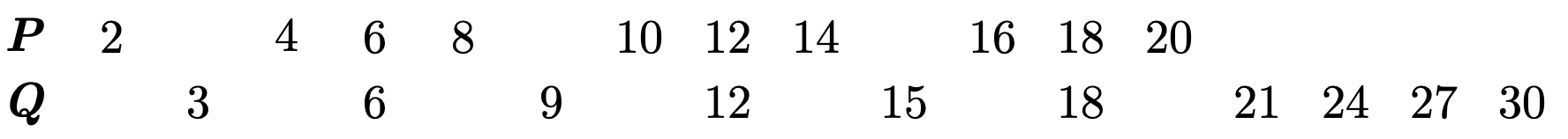
Для всех остальных неважно наличие условия           

x \in A

Но ищется наибольшая возможная мощность    .

A

Выбираем оставшиеся эл-ты

\Rightarrow A = \{2,4,8,10,14,16,20 \}; |A| = 7.

Ответ: 7.

x

Решение:

Задачи

\bigl((x \in P) \rightarrow (x \in A)\bigr) \vee \bigl(!(x \in A) \rightarrow !(x \in Q) \bigr).
A

3. Элементами множеств                являются натуральные числа, причём

 

Определить наименьшее возможное количество элементов в множестве   , таких, чтобы следующее выражение было истинным при любом значении   .

A, P, Q
Q = \{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\}.
P = \{2, 4, 6, 8, 10, 12, 14, 16, 18, 20\},
x

2. На числовой прямой задан отрезок    . Известно, что формула

 

тождественно истинна при любом вещественном   . Какую наименьшую длину может иметь отрезок    ?

A
\bigl( (x \in A) \rightarrow (x^2 \le 100) \bigr) \wedge \bigl( (x^2 \le 64) \rightarrow (x \in A) \bigr)
x
A

1. Сколько существует целых значений числа     , при которых формула

 

тождественно истинна при любых целых неотрицательных    и    ?

\bigl( (x < A) \rightarrow (x^2 < 100) \bigr) \wedge \bigl( (y^2 \le 64) \rightarrow (y \le A) \bigr)
A
x
y

Пример III-1

Для какого наименьшего целого неотрицательного числа     выражение

 

тождественно истинно при любых целых неотрицательных     и    ?

A
(y + 2x < A) \vee (x > 15) \vee (y > 30)
x
y

Строим графики каждого дизъюнкта и их области:

Решение:

(y + 2x < A) \vee (x > 15) \vee (y > 30)
y = -2x + A\\
x = 15\\
y = 30
y=30
x=15
x
y
0
y = -2x + A\\

Каким должен быть параметр     , чтобы в области       выполнялось условие 

D_1
D_2
D_3
D_4
A
D_1
y + 2x < A?
y < -2x + A\\
y > -2x + A\\
30
15
(15; 30)

Необходимо, чтобы он проходил через точку (15; 30)

y + 2x < A \Bigr|_{x=15;y=30} \Rightarrow 30 + 2 \cdot 15 < A \Rightarrow A > 60\\ \Rightarrow A_{\min} = 61.

Ответ: 61.

Пример III-2

Для какого наименьшего целого неотрицательного числа     выражение

 

тождественно истинно при любых целых неотрицательных     и    ?

A
(x + 2y < A) \vee (y > x) \vee (x > 30)
x
y

Ответ: 91.

Пример III-3

Для какого наибольшего целого неотрицательного числа      выражение

 

тождественно истинно при любых целых неотрицательных     и     ?

A
(2x + 3y < 30) ∨ (x + y ≥ A)
x
y

Ответ: 10.

Пример III-4

Для какого наименьшего целого неотрицательного числа     выражение

 

тождественно истинно при любых целых неотрицательных     и     ?

A
(3x + 4y \ne 70) ∨ (A > x) ∨ (A > y)
x
y

Ответ: 11.

Пример III-5

Для какого наименьшего целого неотрицательного числа     выражение

 

тождественно истинно при любых целых неотрицательных     и    ?

A
(2x + 3y \ne 60) ∨ (A ≥ x) ∨ (A ≥ y)
x
y

Ответ: 12.

Made with Slides.com