Объёмы тел

11 класс

 

vkrysanov320@gmail.com

version 1.0, 19-01-2021

Выч-е объемов (интегральный пдх. (I))

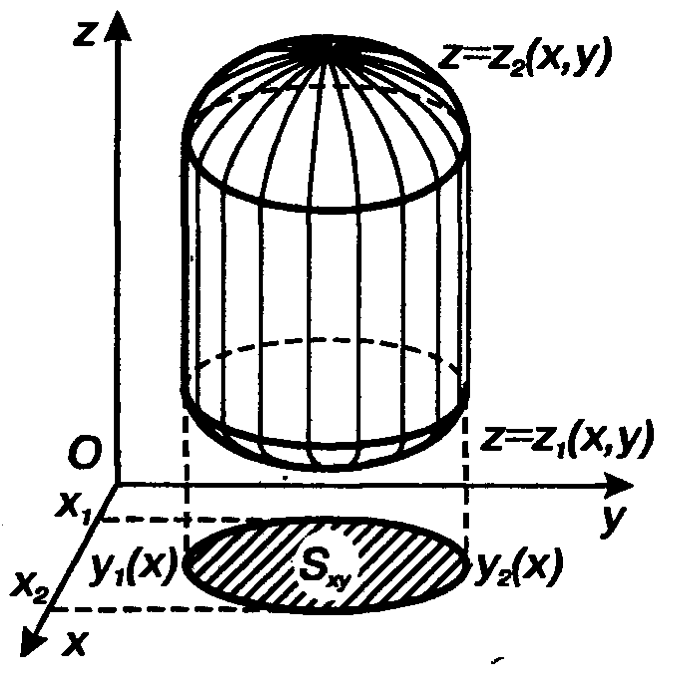
V = \iiint\limits_V dxdydz = \int\limits_{x_1}^{x_2}dx \int\limits_{y = y_1(x)}^{y=y_2(x)}dy \int\limits_{z=z_1(x;y)}^{z=z_2(x;y)}dz.

Выч-е объемов (интегральный пдх. (II))

\Delta x
a
b
x
S(x)

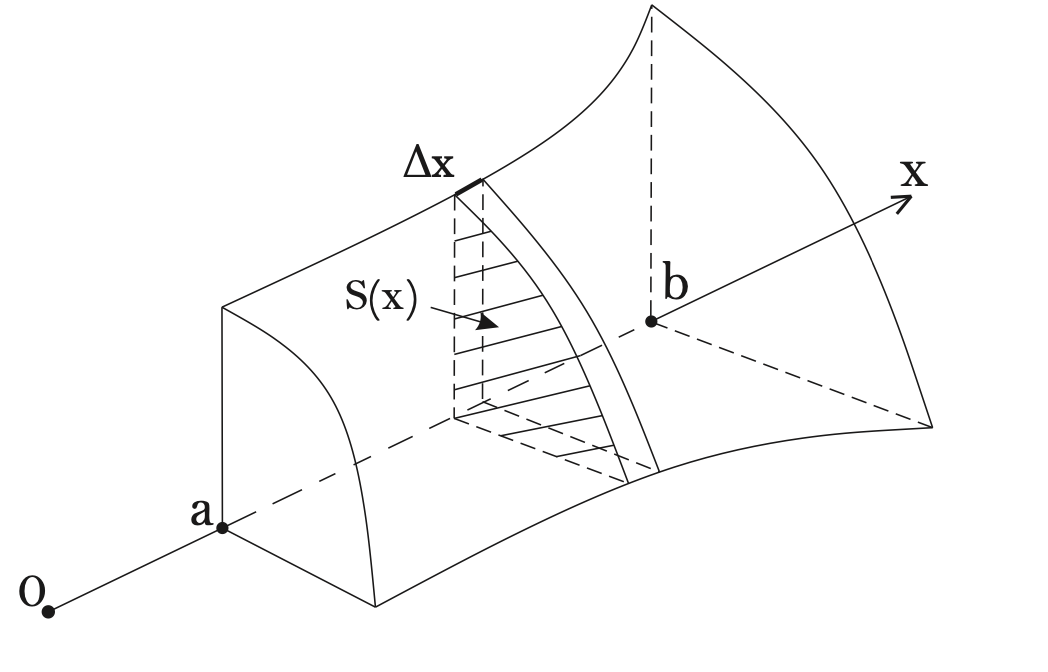
Выч-е объемов тел вращения

\displaystyle{V = \int\limits_a^b S(x)dx = \int\limits_a^b \pi f^2(x)dx = \pi \int\limits_a^b f^2(x)dx.}
f(x)
S(x) = \pi R^2\Bigl|_{R = f(x)} = \pi f^2(x)

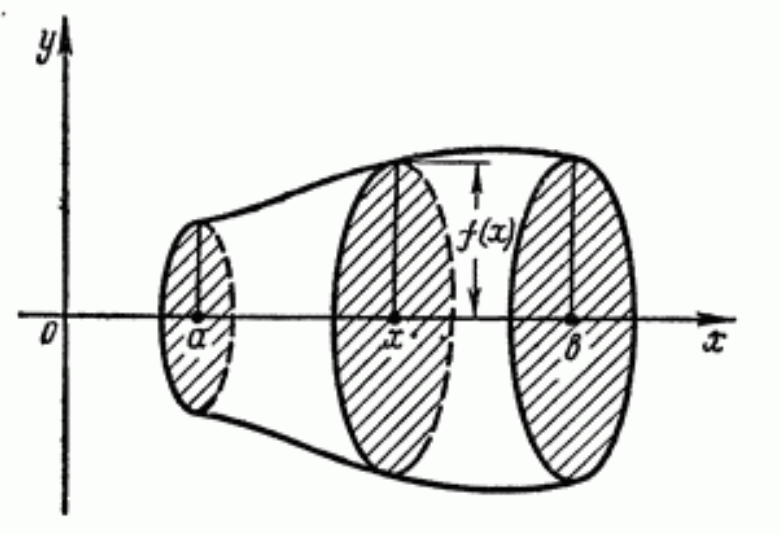
Поперечными сечениями будут круги с радиусами, равными модулю ординаты у вращающейся кривой:

Телом вращения называется тело, образованное вращением плоской фигуры вокруг прямой, лежащей в плоскости этой фигуры. В роли плоской фигуры может выступать криволинейная трапеция, заданная функцией         , как показано на рисунке ниже.

f(x)

Тогда, применяя интегральный подход II, получаем:

Объем прямого параллелепипеда

V = \int\limits_0^{H} S(x) dx \xRightarrow{S=const} \int\limits_0 ^H S_{\text{осн}} dx =
S_{\text{осн}} x \Bigl|_0 ^H = S_{\text{осн}}(H - 0) = S_{\text{осн}}H.
V = S_{\text{осн}}H
S(0)
x_i
H

*Площадь не изменится в любой точке отрезка от    до      и равна площади основания

0
H
S(0) = S(x_1) = ... = S(x_n)
0
S(x_i)
S(H)
x_i
H
x

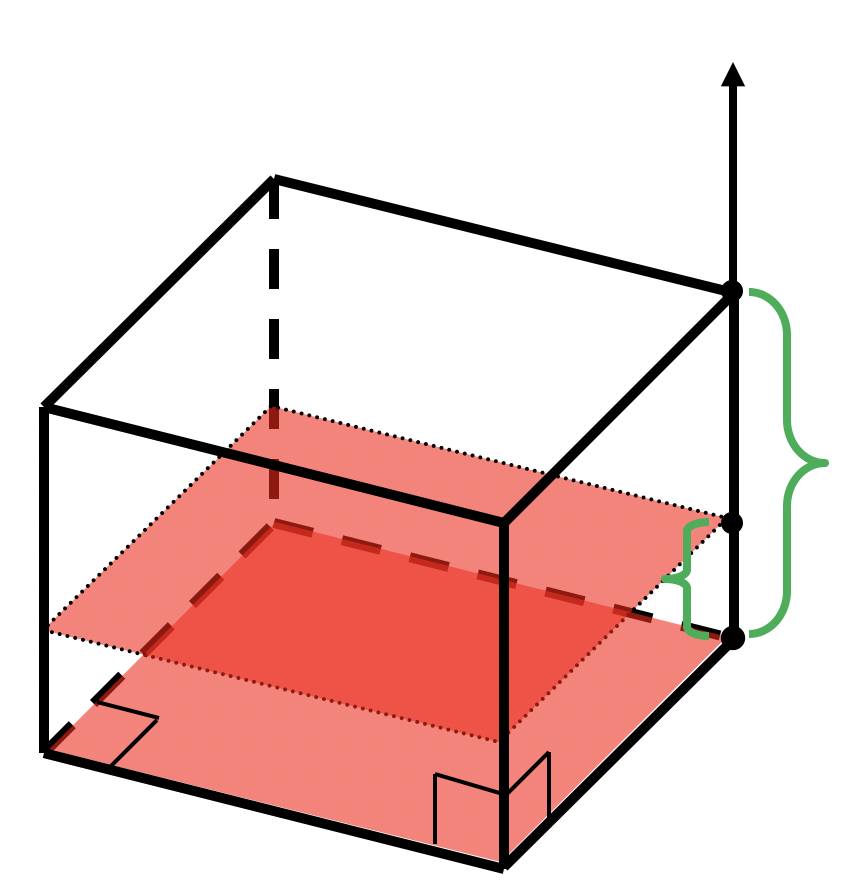
Объем прямой призмы

V = S_{\text{осн}}H
S(0)
x_i
H

*Площадь не изменится в любой точке отрезка от    до      и равна площади основания

0
H
S(0) = S(x_1) = ... = S(x_n)
0
S(x_i)
S(H)
x_i
H
x
V = \int\limits_0^{H} S(x) dx \xRightarrow{S=const} \int\limits_0 ^H S_{\text{осн}} dx =
S_{\text{осн}} x \Bigl|_0 ^H = S_{\text{осн}}(H - 0) = S_{\text{осн}}H.

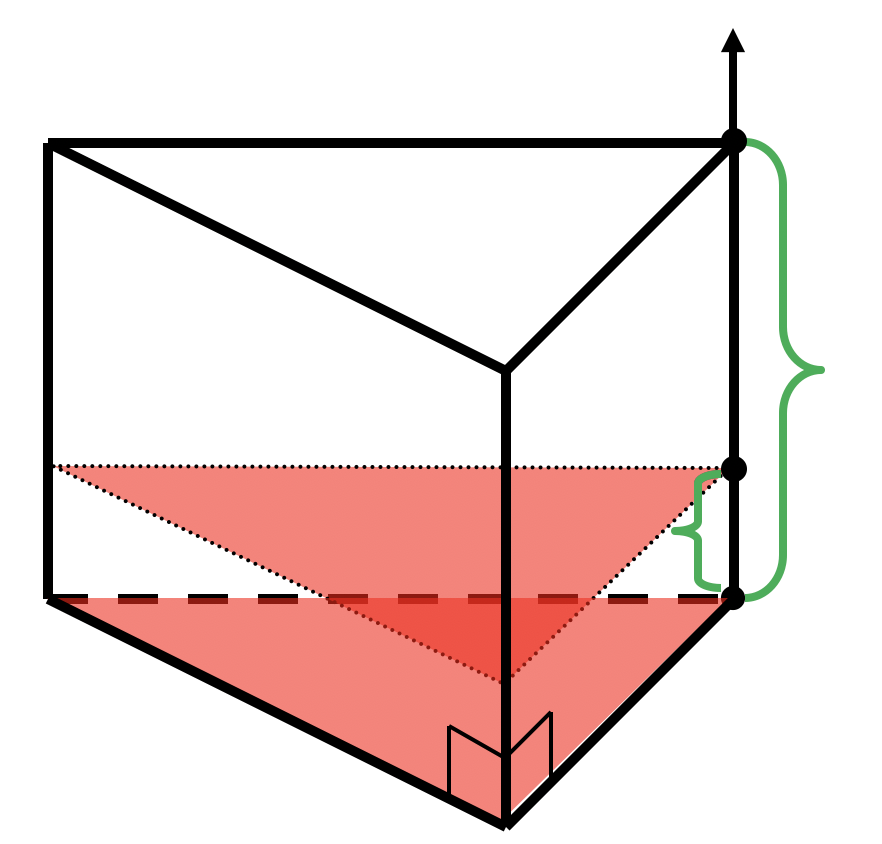
Объем прямой n-угольной призмы

V = S_{\text{осн}}H
S(0)
x_i
H

*Площадь не изменится в любой точке отрезка от    до      и равна площади основания

0
H
S(0) = S(x_1) = ... = S(x_n)
0
S(x_i)
S(H)
x_i
H
x
V = \int\limits_0^{H} S(x) dx \xRightarrow{S=const} \int\limits_0 ^H S_{\text{осн}} dx =
S_{\text{осн}} x \Bigl|_0 ^H = S_{\text{осн}}(H - 0) = S_{\text{осн}}H.

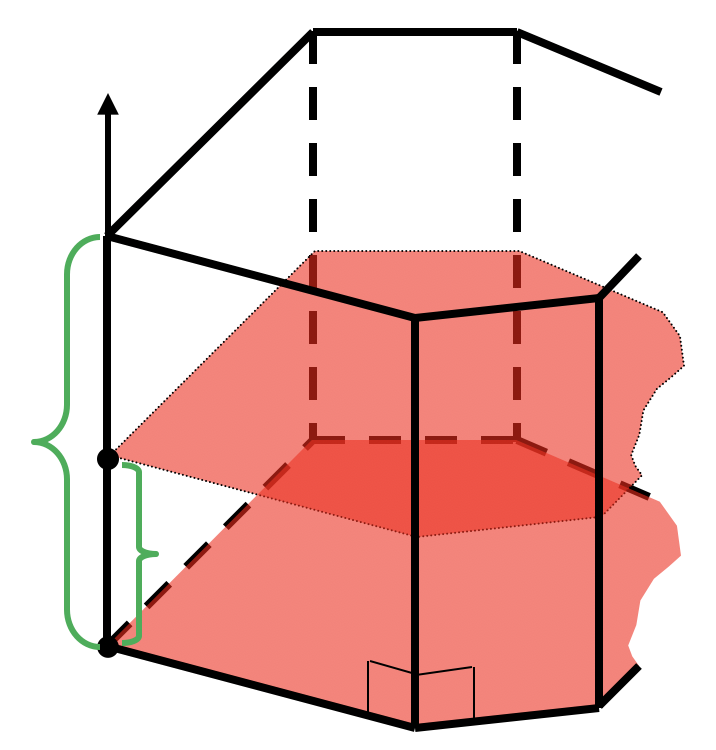
Объем наклонной призмы

V = S_{\text{осн}}H
S(0)
x_i
H

*Площадь не изменится в любой точке отрезка от    до      и равна площади основания

0
H
S(0) = S(x_1) = ... = S(x_n)
0
S(x_i)
S(H)
x_i
H
x
V = \int\limits_0^{H} S(x) dx \xRightarrow{S=const} \int\limits_0 ^H S_{\text{осн}} dx =
S_{\text{осн}} x \Bigl|_0 ^H = S_{\text{осн}}(H - 0) = S_{\text{осн}}H.

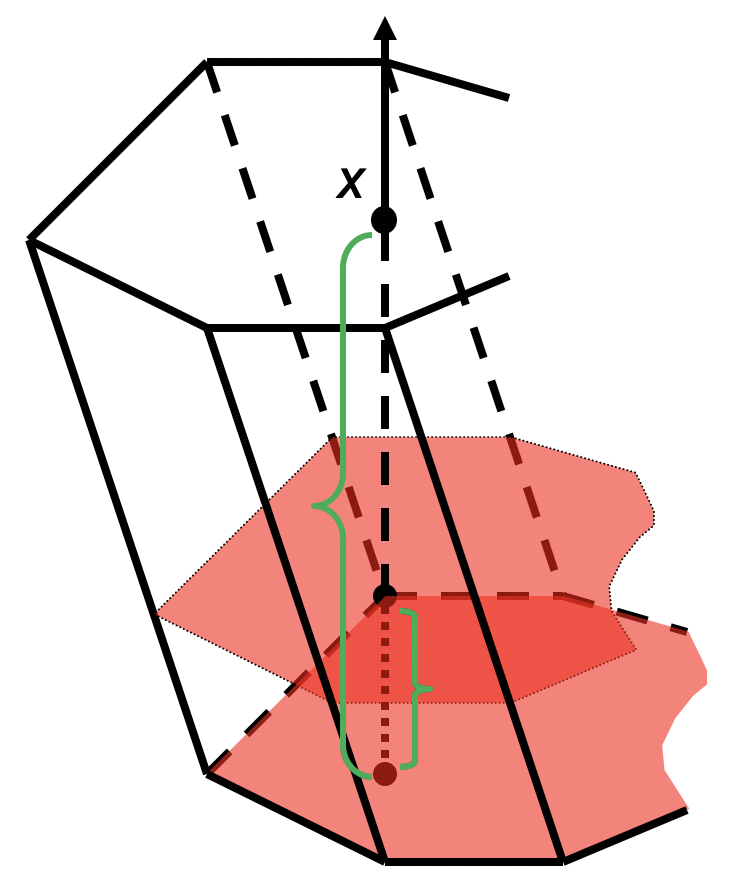
Объем треугольной пирамиды

V = \int\limits_0^{H} S(x) dx \xRightarrow{S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}} \int\limits_0 ^H \frac{S_{\text{ осн}} \cdot x^2}{H^2} dx =
V = \frac13 S_{\text{ осн}} H
S(0)
x_i
H

*Площадь сечения изменяется в зависимости от расстояния    , причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных тругольниках:

0
S(x_i)
x_i
H
x
x
\frac{S_{\text{ осн}}}{S(x)} = \bigl(\frac{H}{x}\bigr)^2 \Rightarrow S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}
= \frac{S_{\text{ осн}}}{H^2} \int\limits_0 ^H x^2 dx = \frac{S_{\text{ осн}}}{H^2} \frac{x^3}{3} \Bigl|_0^ H = \frac13 S_{\text{ осн}} H.

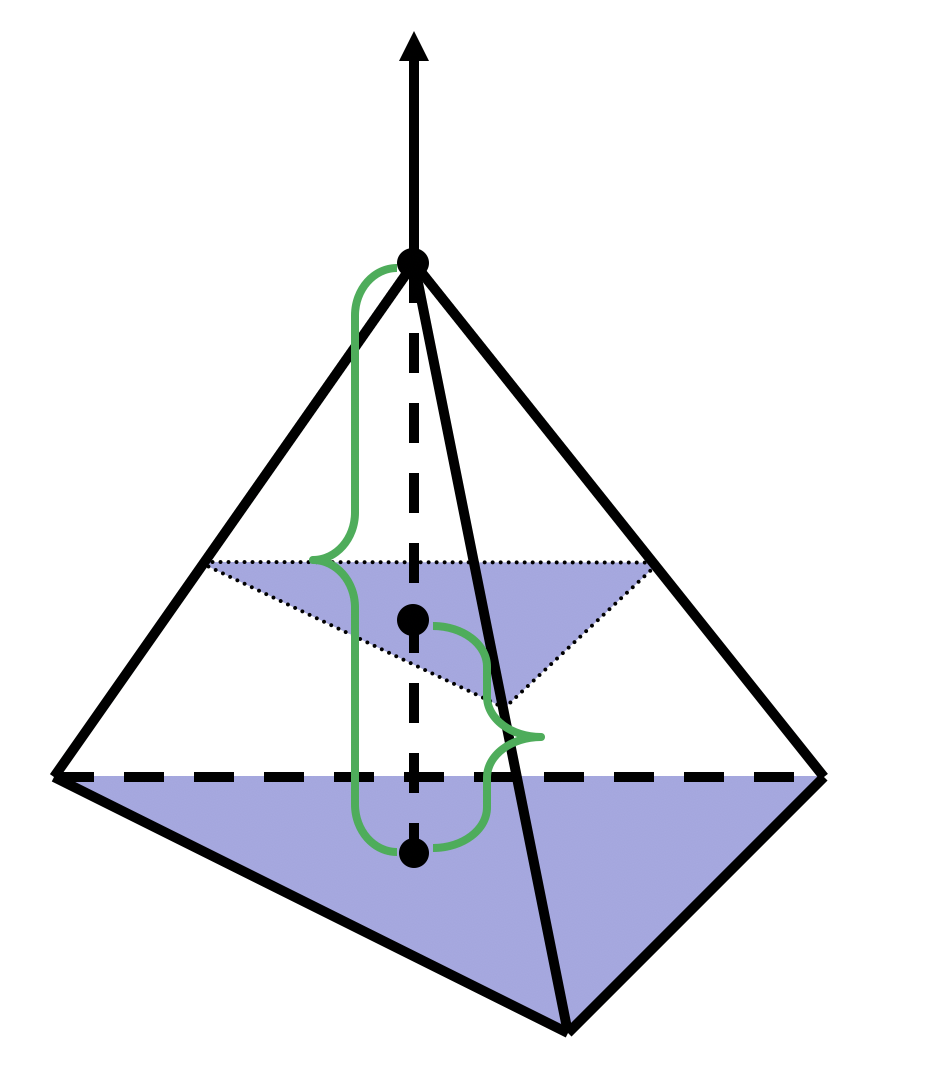
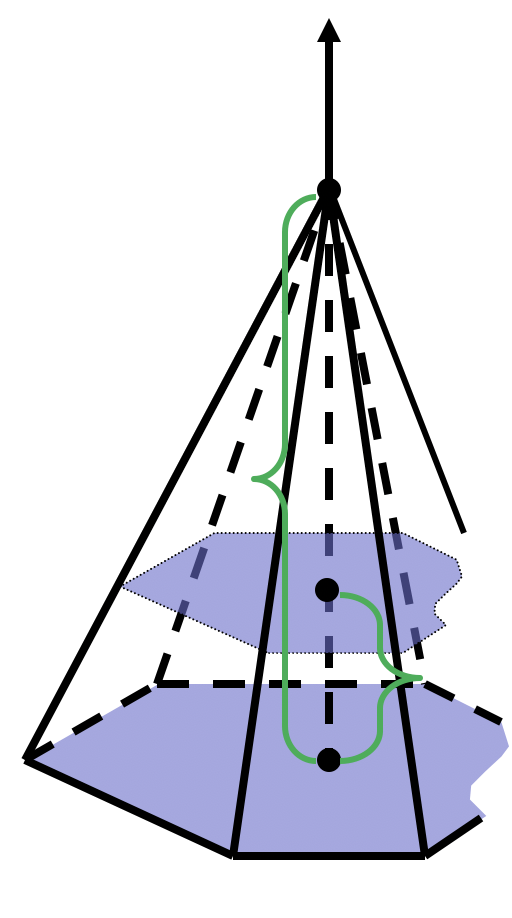
Объем n-угольной пирамиды

V = \int\limits_0^{H} S(x) dx \xRightarrow{S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}} \int\limits_0 ^H \frac{S_{\text{ осн}} \cdot x^2}{H^2} dx =
V = \frac13 S_{\text{ осн}} H
S(0)
x_i
H

*Площадь сечения изменяется в зависимости от расстояния    , причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных n- угольниках:

0
S(x_i)
x_i
H
x
x
\frac{S_{\text{ осн}}}{S(x)} = \bigl(\frac{H}{x}\bigr)^2 \Rightarrow S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}
= \frac{S_{\text{ осн}}}{H^2} \int\limits_0 ^H x^2 dx = \frac{S_{\text{ осн}}}{H^2} \frac{x^3}{3} \Bigl|_0^ H = \frac13 S_{\text{ осн}} H.

Объем цилиндра

S(0)
x_i
H
0
S(x_i)
x_i
H
x
V = \int\limits_0^{H} S(x) dx \xRightarrow{S=const} \int\limits_0 ^H S_{\text{осн}} dx =
S_{\text{осн}} x \Bigl|_0 ^H = S_{\text{осн}}(H - 0) = S_{\text{осн}}H.

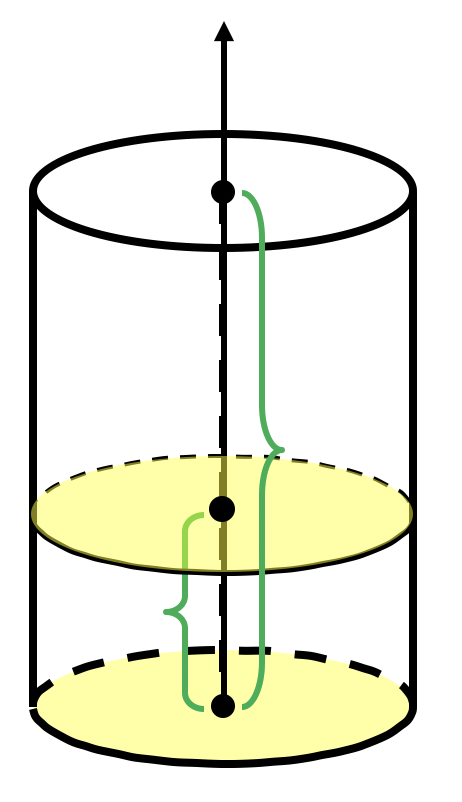
*Площадь не изменится в любой точке отрезка от    до      и равна площади основания

0
H
V = S_{\text{осн}}H
S(0) = S(x_1) = ... = S(x_n)
S(H)

Объем конуса

S(0)
x_i
H
0
S(x_i)
x_i
H
x
V = \int\limits_0^{H} S(x) dx \xRightarrow{S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}} \int\limits_0 ^H \frac{S_{\text{ осн}} \cdot x^2}{H^2} dx =
V = \frac13 S_{\text{ осн}} H

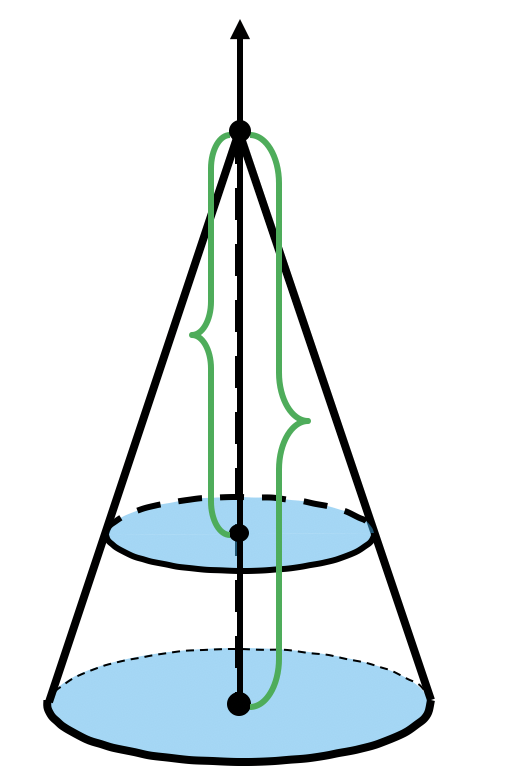
*Площадь сечения изменяется в зависимости от расстояния    , причем отношение площади основания к площади сечения равно квадрату коэффициента подобия соответственных кругов:

x
\frac{S_{\text{ осн}}}{S(x)} = \bigl(\frac{H}{x}\bigr)^2 \Rightarrow S(x) = \frac{S_{\text{ осн}} \cdot x^2}{H^2}
= \frac{S_{\text{ осн}}}{H^2} \int\limits_0 ^H x^2 dx = \frac{S_{\text{ осн}}}{H^2} \frac{x^3}{3} \Bigl|_0^ H = \frac13 S_{\text{ осн}} H.

Объем шара

S(0)
x_i
0
S(x_i)
x_i
R
x
r
S(x) = \pi r^2 = \pi(\sqrt{R^2 - x^2})^2 = \pi(R^2 - x^2)
= \pi \int\limits_0^R (R^2 - x^2) dx = \pi \int\limits_0^R R^2 - \pi \int\limits_0^R x^2dx =
V_{\frac{1}{2} шара} = \int\limits_0^{R} S(x) dx \xRightarrow{S(x) = \pi(R^2 - x^2)} \int\limits_0^R \pi(R^2 - x^2) dx =
= \pi \int\limits_0^R (R^2 - x^2) dx = \pi \int\limits R^2 dx - \pi \int\limits_0^R x^2dx =
= \pi R^2 x \Bigl |_{0}^{R} - \pi \frac{x^3}{3} \Bigl |_{0}^R = \pi R^3 - \frac{\pi R^3}{3} = \frac{2\pi R^3}{3}.
\Rightarrow V_{шара} = 2{V_{\frac{1}{2}шара}} = 2 \frac{2\pi R^3}{3} = \frac{4}{3}\pi R^3.
V = \frac{4}{3}\pi R^3

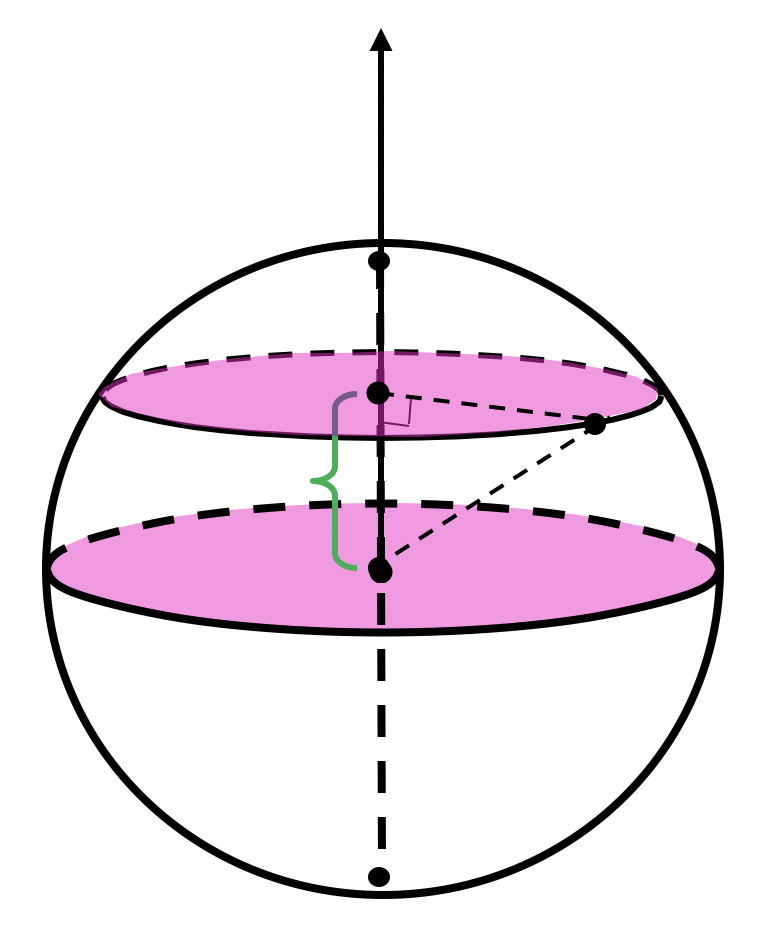
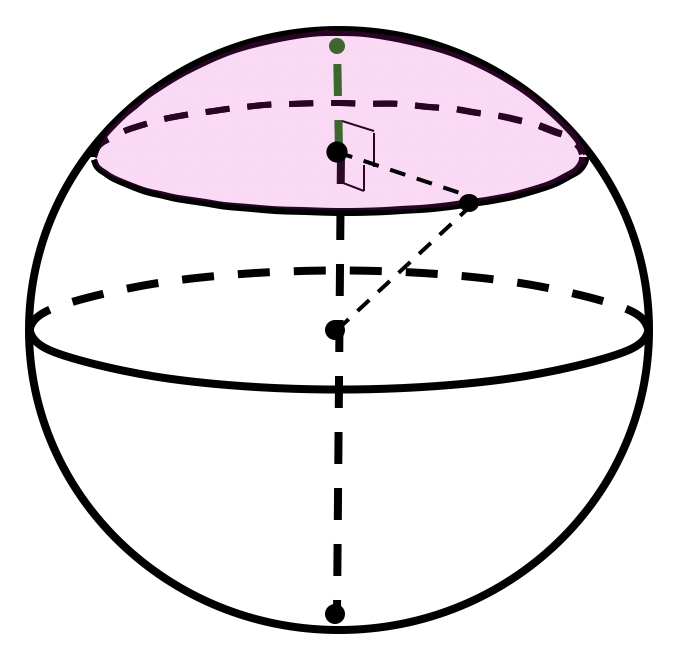
Шаровой сегмент

Шаровой сегмент — часть шара, отсекаемая от него плоскостью.

\alpha
AB

 — высота шарового сегмента.

S = 2\pi Rh

Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью) вычислить как:

Объем шарового сегмента

R-h
0
r
R

*Вывод объема шарового сегмента с высотой     и радиусом основания     отличается от вывода объема полушария нижним пределом интегрирования. В данном случае он равен             :

h
r
R-h
V_{ш. сегм.} = \int\limits_{R-h}^{R} S(x) dx \xRightarrow{S(x) = \pi(R^2 - x^2)} \int\limits_{R-h}^R \pi(R^2 - x^2) dx =
=\int\limits_{R-h}^R \pi(R^2 - x^2) dx = \pi \int\limits_{R-h}^R R^2 dx - \pi \int\limits_{R-h}^R x^2 dx =
=\pi \Bigl(R^2 x - \frac{x^3}{3} \Bigr)\Bigl |_{R-h}^R = \pi \Bigl(R^2 R - \frac{R^3}{3} - \bigl(R^2(R-h) - \frac{(R-h)^3}{3}\bigr)\Bigr)=
\pi\Bigl(\frac{2 R^3}{3}- R^3 + R^2h + \frac{R^3-3R^2h + 3Rh^2 - h^3}{3}\Bigr ) = \pi(Rh^2 - \frac{h^3}{3}) = \pi h^2(R - \frac{h}{3}).
V = \pi h^2(R - \frac{h}{3})
R

Шаровой слой (пояс)

Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

\alpha
AB

 — высота шарового слоя.

\beta
S = 2\pi Rh

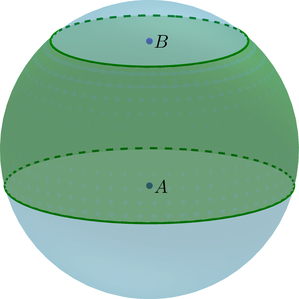
Площадь сферической части шарового слоя равна:

Объем шарового слоя

A
B
C
AC
BC

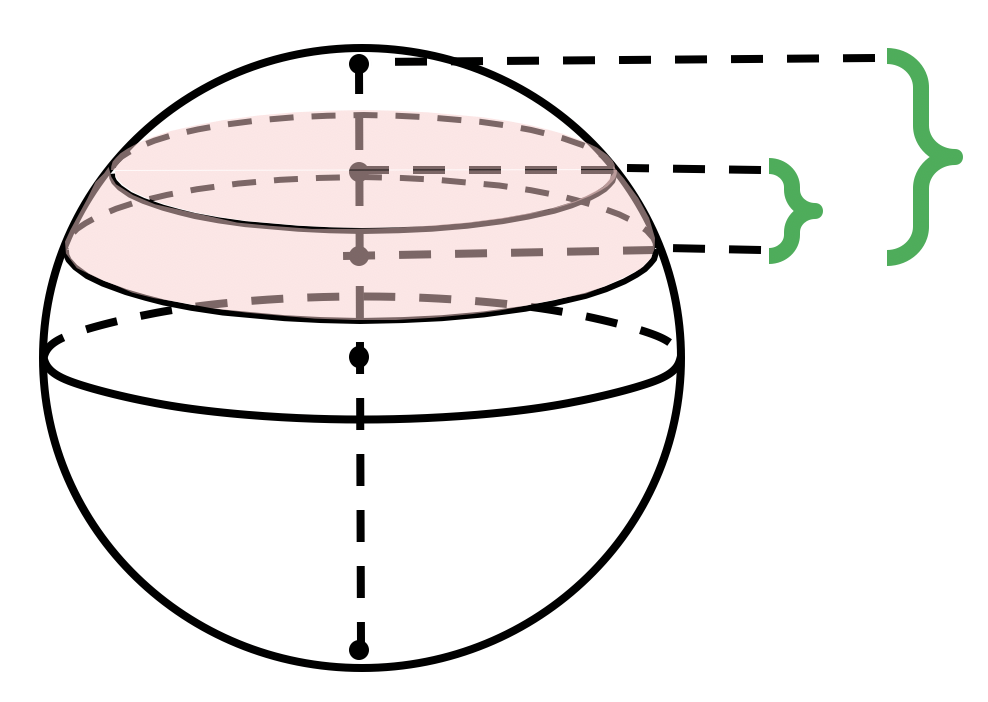
Объем шарового слоя равен разности объемов двух шаровых сегментов:
 

V = V_{AC} - V_{BC}

Шаровой сектор

Шаровой сектор — часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

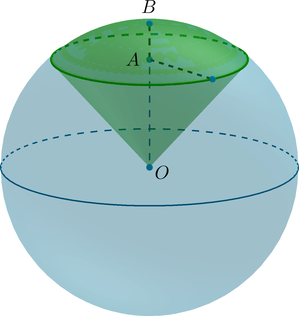
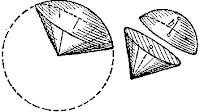
Объем шарового сектора

Шаровой сектор состоит из шарового сегмента и конуса, значит объем шарового сектора равен:

V = V_{конус} + V_{ш. сек.}
V_{конус} = \frac{1}{3}\pi r^2 (R-h) \Bigl|
h
r
R
O
V_{ш.сег.} = \pi h^2(R - \frac{h}{3}).
r = \sqrt{R^2 - (R-h)^2} =\\= \sqrt{R^2 - [R^2 - 2Rh + h^2]} =\\= \sqrt{2Rh - h^2} = \sqrt{h(2R - h)}
V_{конус} = \frac{1}{3}\pi r^2 (R-h) \Bigl|
= \frac{1}{3}\pi h(2R - h) (R-h).
\Bigl| =
V = \frac{1}{3}\pi h(2R - h) (R-h) + \pi h^2(R - \frac{h}{3}) = \frac{1}{3}\pi h(2R - h) (R-h) + \frac{1}{3}\pi h^2(3R - h) = \frac{2}{3}\pi R^2 h.

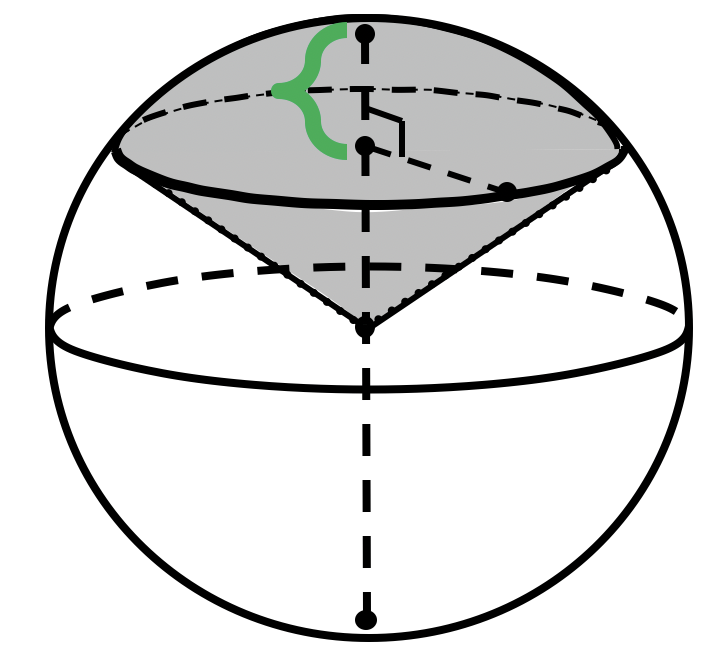
Тогда:

V = \frac{2}{3}\pi R^2 h

Задачи

1. Найти объем цилиндра, диаметр основания которого равен его высоте, а площадь осевого сечения равна 16.

 

2. Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

 

3. Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в 343 раза больше объема второго шара?

 

4. Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.

Задачи (2)

5. В сосуд цилиндрической формы, объем которого 2400 кубических сантиметра, налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.

 

6. В одном основании прямого кругового цилиндра с высотой 12 и радиусом основания 6 проведена хорда       , равная радиусу основания, а в другом его основании проведён диаметр       , перпендикулярный       . Построено сечение              , проходящее через прямую        перпендикулярно прямой         так, что точка      и центр основания цилиндра, в котором проведён диаметр        , лежат с одной стороны от сечения.

    а) Докажите, что диагонали этого сечения равны между собой.

    б) Найдите объём пирамиды                  .

CABNM
AB
CD
AB
ABNM
AB
C
CD
CD
Made with Slides.com