Теория чисел

10-11 класс

 

vkrysanov320@gmail.com

version 2.2, 11-09-2022

Некоторые операции со множествами

Объединение

A \cup B
A
B
A
B
A \setminus B

Разность

A \cap B

Пересечение

A
B
A
B
A \subset B

Подмножество (строго):

или

B \supset A

Подмножество (не строго):

A \subseteq B

или

B \supseteq A

Работает так же как и 

>, \ge, <, \le.

Иерархия чисел

\mathbb{C}

комплексные

\mathbb{R}

вещественные

 (действительные)

\mathbb{N}

натуральные

\mathbb{Z}

целые

\mathbb{Q}

рациональные

\mathbb{I}

иррациональные

Натуральные числа

\mathbb{N} = \{1; 2; 3; ...\}.

Натуральные числа — числа, получаемые при естественном счёте:

 

 

* Иногда к множеству натуральных чисел также относят ноль:

\mathbb{N}_0 = \{0, 1; 2; 3; ...\}.

Операции над натуральными числами

  • сложение
  • умножение
  • возведение в степень

операции, не выводящие результат из множества натуральных чисел (замкнутые операции)

Дополнительно рассматривают ещё две операции (с формальной точки зрения не являющиеся операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет)):

  • сложение
  • умножение
  • возведение в степень
  • вычитание
  • деление с остатком:
a = p \cdot b + r, r < b

Свойства натуральных чисел

a + b = b + a

1. Коммутативность сложения:

2. Коммутативность умножения:

a \cdot b = b \cdot a

3. Ассоциативность сложения:

(a + b) + c = a + (b + c)

4. Ассоциативность умножения:

(a \cdot b) \cdot c = a \cdot (b \cdot c)

5. Дистрибутивность умножения относительно сложения:

{\displaystyle {\begin{cases}a\cdot (b+c)=a\cdot b+a\cdot c\\(b+c)\cdot a=b\cdot a+c\cdot a\end{cases}}}

Основная теорема арифметики (ОТА)

n > 1

Каждое натуральное число           можно факторизовать (разложить) в виде                  ,      

где                — простые числа, причём такое представление единственно, если не учитывать порядок следования множителей. 

p_1 \cdot ... \cdot p_k
p_1, ..., p_k

Простое число — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число    является простым, если оно отлично от    и делится без остатка только на    и на само себя.

p
1
1
102
2
51
3
17
17
1
\Rightarrow\mathrm{factor} (102) = 2 \cdot 3 \cdot 17.
23244
2
2
3
11622
5811
1937
13
149
149
1
\Rightarrow\mathrm{factor} (23244) = 2^2 \cdot 3 \cdot 13 \cdot 149.
n = p_1^{d_1} \cdot p_2^{d_2} \cdot ... \cdot p_k^{d_k}

, где                               — простые числа, а

p_1 < p_2 < ... < p_k
d_1, ..., d_k

— некоторые натуральные числа.

Каноническое разложение

Примеры факторизации:

3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 ​47 48 49 50
51 ... ... ... ... ... ... ... ... ...

Решето Эратосфена

4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 ​47 48 49 50
51 ... ... ... ... ... ... ... ... ...

2

3

2

4 6 8 9 10
12 14 15 16 18 20
21 22 24 25 26 27 28 30
32 33 34 35 36 38 39 40
42 44 45 46 ​ 48 49 50
51 ... ... ... ... ... ... ... ... ...

2

3

5

7

11

13

17

19

23

29

31

41

43

47

37

\Rightarrow \mathrm{prime}: 2, 3, 5, 7, 11, 13, 17, 19, 23,
31, 37, 41, 43, 47, ...

1. Запишем натуральные числа, начиная от    , до    (в данном случае до      ). Первое число в списке,    — простое. Пройдем по ряду чисел, зачеркивая все числа, кратные    (то есть, каждое второе, начиная с             ).

n
2
51
2
2
2^2 = 4

2. Следующее незачеркнутое число,    — простое. Пройдем по ряду чисел, зачеркивая все числа, кратные (то есть, каждое третье, начиная с             ).

3
3
3^2 = 9

3. И так далее ... Оставшиеся числа будут простые, так как все составные уже зачеркнуты.

Признак делимости Паскаля

A=\overline {a_{n}a_{{n-1}}\ldots a_{2}a_{1}a_{0}}

 — остаток от деления              на      ; 

 — остаток от деления              на     ; 

 — остаток от деления              на     ;

...

 — остаток от деления                 на     .

r_1
r_2
r_3
r_n
10 \cdot r_0
m
10 \cdot r_1
10 \cdot r_2
10 \cdot r_{n-1}
m
m
m
\begin{cases} \\\\\\\\\\ \end{cases}
A

      имеет тот же остаток при делении на    , что и

a_0 + r_1 \cdot a_1 + r_2 \cdot a_2 + ... + r_n \cdot a_n
m
r_0 = 1

Признак делимости Паскаля. Пример

т. д.:                   (или можно записать                                ) по признаку

48916\text{ }\mathrm{mod} \text{ }7 = 0
48916 \text{ }\vdots \text{ }7

делимости Паскаля.

m = 7:
10 \cdot r_0 =1\cdot 7+3\Rightarrow r_{1}=3
10\cdot r_{1}=4\cdot 7+2\Rightarrow r_{2}=2
10\cdot r_{2}=2\cdot 7+6\Rightarrow r_{3}=6
10\cdot r_{3}=8\cdot 7+4\Rightarrow r_{4}=4
10\cdot r_{4}=5\cdot 7+5\Rightarrow r_{5}=5
10\cdot r_{5}=7\cdot 7+1\Rightarrow r_{6}=1
\circlearrowright

Цикл

\begin{cases} \\\\\\\\\\ \end{cases}
48916\text{ }\mathrm{mod}\text{ } 7 = (a_{0}+3a_{1}+2a_{2}+6a_{3}+4a_{4}+5a_{5}+a_{6}+\ldots)\text{ } \mathrm{mod}\text{ } 7
48916 \equiv 6+3\cdot 1+2\cdot 9+6\cdot 8+4\cdot 4 \text{ }(\mathrm{mod} \text{ }7);

Тогда:

48916 \equiv 6+3+18+48+16 \text{ }(\mathrm{mod} \text{ }7);
48916 \equiv 91 \text{ }(\mathrm{mod} \text{ }7);
48916 \equiv 0 \text{ }(\mathrm{mod} \text{ }7).
\Rightarrow 48916 \text{ }\vdots \text{ }7.

Задачи

1. Разложить число 2016 на простые множители.

2. Произведение двух натуральных чисел, каждое из которых не делится нацело на 10, равно 10000. Найти сумму этих чисел.

3. Существует ли целое число, произведение цифр которого равно 594?

4. Существует ли целое число, произведение цифр которого равно 1330?

5. Доказать, что произведение любых трёх последовательных целых чисел делится на 3?

6. Доказать, что произведение любых трёх последовательных целых чисел делится на 6?

7. Доказать, что число              делится на 6 при любом целом    .

n^3 - n
n

Как доказать справедливость следующей формулы?

1 + 2 + 3 + ... + n = \frac{n(n+1)}{2}.

Метод математической индукции

Метод математической индукции

Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел.

Принцип:

Пусть доминошки выставлены на ребро друг за другом. Нам необходимо доказать следующий факт:

«Если толкнуть первую доминошку, то для любого сколь угодно большего      доминошка с номером когда-нибудь упадет.»

N
N

Для доказательства понадобится установить верность двух утверждений:

1) База индукции: Мы можем толкнуть первую доминошку и она упадет.

2) Индукционный переход: Если падает доминошка с номером    , то она толкает доминошку с номером

k+1.
k

Метод математической индукции. Теперь более формально...

Пусть имеется последовательность утверждений:                                 . Для того чтобы доказать справедливость всех утверждений этой последовательности, необходимо поступить следующим образом:

1) База индукции: Доказать истинность утверждения     .

2) Индукционный переход: Доказать, что при любом натуральном     из справедливости утверждения       следует справедливость утверждения          .

P_1, P_2, P_3, ... P_n, ...
P_1
P_n
P_{n+1}
n

Пример 1

Доказать справедливость формулы:

1 + 2 + 3 + ... + n = \frac{n(n+1)}{2}.

Решение:

1) База индукции              :

1 = \frac{1(1+1)}{2} \Rightarrow 1 = 1.

(база индукции доказана)

2) Индукционный переход:

предположим, что для            выполнено

тогда для                   согласно предположению:

1 + 2 + 3 + ... + k = \frac{k(k+1)}{2},
(n=1)
n = k
n = k + 1
{\underbrace{1 + 2 + 3 + ... + k}_{\frac{k(k+1)}{2}}} + (k + 1) = \frac{k(k+1)}{2} + (k + 1) = \frac{k(k+1) + 2(k+1)}{2} = \frac{k^2 + k + 2k + 2}{2} = \frac{k(k + 1) + 2(k + 1)}{2} =
= \frac{(k + 1)(k + 2)}{2}.

Значит по принципу математической индукции выполнено равенство для всякого   .

n
P_{k+1}

(индукционное предположение)

Пример 2

Доказать справедливость формулы:

1 + 3 + 5 + ... + (2n-1) = n^2.

Решение:

1) База индукции              :

1 = 1^2 \Rightarrow 1 = 1.

(база индукции доказана)

2) Индукционный переход:

предположим, что для            выполнено

тогда для                   согласно предположению:

1 + 3 + 5 + ... + (2k - 1) = k^2,
(n=1)
n = k
n = k + 1
{\underbrace{1 + 3 + 5 + ... + (2k - 1)}_{k^2}} + (2(k+1) - 1) = k^2 + (2(k+1) - 1) = k^2 + 2k + 2 - 1 =
= k^2 +2k + 1 = (k+1)^2.

Формула справедлива для любого натурального

n.
P_{k+1}

(индукционное предположение)

\Rightarrow

Пример 3

Доказать справедливость формулы:

(13^n + 5) \text{ } \vdots \text{ } 6.

Решение:

1) База индукции              :

(13^1 + 5) \text{ } \vdots \text{ } 6 \Rightarrow 1 = 18 \text{ } \vdots \text{ } 6.

(база индукции доказана)

2) Индукционный переход:

предположим, что для            выполнено

тогда для                   согласно предположению:

(13^k + 5) \text{ } \vdots \text{ } 6.
(n=1)
n = k
n = k + 1
(13^{k+1} + 5) = (13 \cdot 13^{k} + 5) = (12 \cdot 13^{k} + {\underbrace{13^k + 5}_{\text{ }}})
\vdots \text{ } 6

Формула справедлива для любого натурального

n.

(индукционное предположение)

\Rightarrow

кратно

6

Первое слагаемое делится на 6 и второе — по индукционному предположению, следовательно и сумма делится на 6.

Задачи

(2^{3n} + 1) \text{ } \vdots \text{ } 3^{n-1}.

1. Доказать справедливость следующих формул при любом натуральном    :

2. На какое число частей могут разделить плоскость     прямых общего положения?

n

a)

(7^{2n} - 1) \text{ } \vdots \text{ } 24;
\sum\limits_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6};

б)

1 \cdot 2 + 2\cdot 3 + 3\cdot 4 + ... + (n-1)n = \frac{(n-1)n(n+1)}{3}, n \ge 2;
n

в)

г)

* Прямые общего положения – это прямые, которые попарно пересекаются, причем никакие три прямые в одной точке не пересекаются.

Целые числа

\mathbb{Z} = \{..., -2; -1, 0; 1; 2; 3; ...\}.

Целые числа — расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел:

 

 

Также можно ввести следующие обозначения:

\mathbb{Z}_{+} = \mathbb{N};\\ \mathbb{Z}_{\ge 0} = \mathbb{N_0};\\ \mathbb{Z}_{-} = \{...; -2; -1\}.

Свойства целых чисел

a + b = b + a

1. Коммутативность сложения:

2. Коммутативность умножения:

a \cdot b = b \cdot a

3. Ассоциативность сложения:

(a + b) + c = a + (b + c)

4. Ассоциативность умножения:

(a \cdot b) \cdot c = a \cdot (b \cdot c)

5. Дистрибутивность умножения относительно сложения:

 

 

 

6. Свойства нуля:

 

7. Свойство противоположного элемента:

{\displaystyle {\begin{cases}a\cdot (b+c)=a\cdot b+a\cdot c\\(b+c)\cdot a=b\cdot a+c\cdot a\end{cases}}}
a + 0 = a;\text{ } a \cdot 0 = 0
-(-a) = a

Понятие модуля

\mathrm{abs}(a) = |a| = \begin{cases} a, \text{ если } a \ge 0;\\ -a, \text{ если } a < 0.\\ \end{cases}

Абсолютной величиной числа    (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат.

 

Из определения следует, что:

a

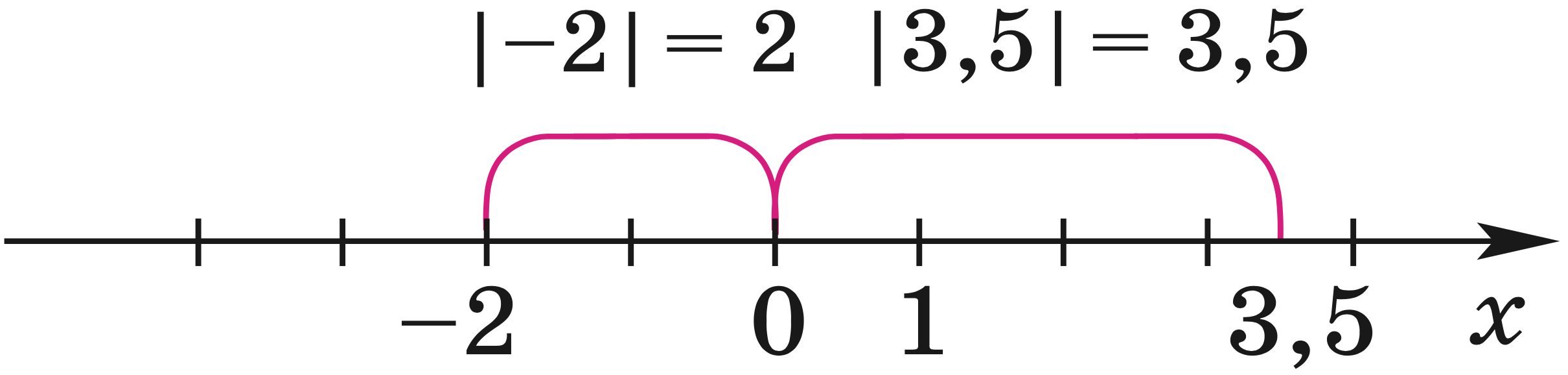
Некоторые свойства модуля:

|a| \ge 0;
|a| = |-a|;

1.

2.

3.

|a \cdot b| = |a| \cdot |b|;

1.

2.

3.

4.

5.

|\frac ab| = \frac{|a|}{|b|}, b \neq 0;
|f(x)| = g(x) \Leftrightarrow \begin{cases} g(x) \ge 0;\\ \left[ \begin{array}{l} f(x) = g(x); \\ f(x) = -g(x);\\ \end{array} \right . \end{cases}
|f(x)| = |g(x)| \Leftrightarrow f^2(x) = g^2(x).
|f(x)| = |g(x)| \Leftrightarrow \left[ \begin{array}{l} f(x) = g(x); \\ f(x) = -g(x);\\ \end{array} \right .

6.

7.

Задачи

\frac{|x-2|-1}{2x-1} = 2;

1. Решить уравнения:

a)

|2x^2 - 1| = x;
|6x^2 - 5x| = 1;

б)

|2x-3| = 2;

в)

г)

д)

е)

|x+2| + 2|x-1|-|x+1| = 3.
\frac{|x| - 3}{|x^2 - 5x - 6} = 1;

Рациональные числа

Рациональные числа —  (от лат. ratio «отношение, деление, дробь») — числа, которые можно представить в виде обыкновенной дроби, где числитель — целое число, а знаменатель — натуральное:

{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} \right\}}.

Периодические дроби

Рациональные числа —  (от лат. ratio «отношение, деление, дробь») — числа, которые можно представить в виде обыкновенной дроби, где числитель — целое число, а знаменатель — натуральное:

{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} \right\}}.

Иррациональные числа

Иррациональные числа — это вещественные числа, которые не является рациональными, то есть не могут быть представлены в виде обыкновенной дроби.

* Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. ​

Комплексные числа

об это потом ...

Made with Slides.com