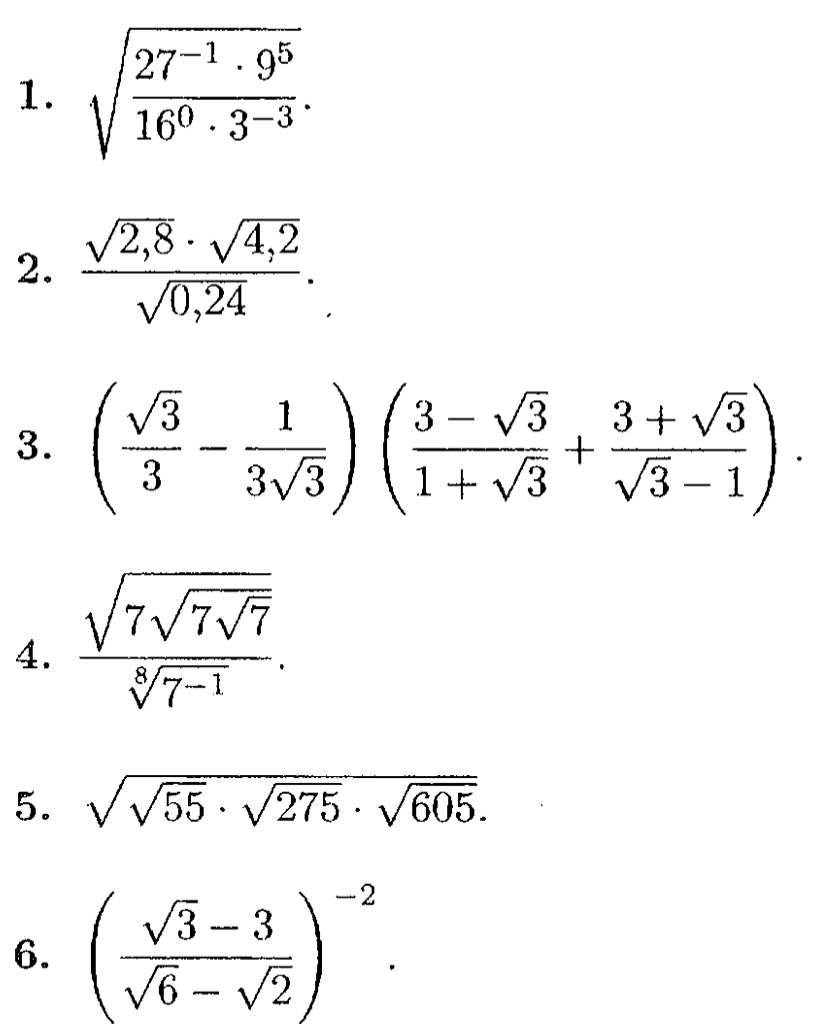Корни. Степени

10-11 класс

vkrysanov320@gmail.com

version 2.1, 07-11-2024 not fixed

Арифметический корень степени n

Неотрицательный корень степени из неотрицательного числа

называют арифметическим корнем степени из числа .

\sqrt[n]{b},

b \ge 0, n \in \mathbb N, n \ge 2

Знак радикала

Подкоренное выражение

Степень

\Rightarrow

Если — отрицательное число, а — четное число, то запись не имеет смысла;

\sqrt[n]{0} = 0, n \ge 2;

\sqrt[n]{1} = 1, n \ge 2;

\sqrt[n]{b}

\sqrt[4]{-9} = \varnothing

\sqrt{-4} = \varnothing

При возведении в четную степень не породнится отрицательное значение (но только для действительных чисел)

Если — положительное число, а — нечетное число, то справедливо следующее равенство:

\sqrt[n]{-b} = -\sqrt[n]{b}.

\sqrt[3]{-8} = -\sqrt[3]{8} = -2

\sqrt[5]{-125} = -\sqrt[5]{125}

\bigl(\sqrt[n]{b}\bigr)^n = b

\sqrt[n]{b^n} = b

График арифметического корня степени n

— четно

f(x) = \sqrt[n]{x}, n

f_1(x) = \sqrt{x}

f_2(x) = \sqrt[4]{x}

f_3(x) = \sqrt[6]{x}

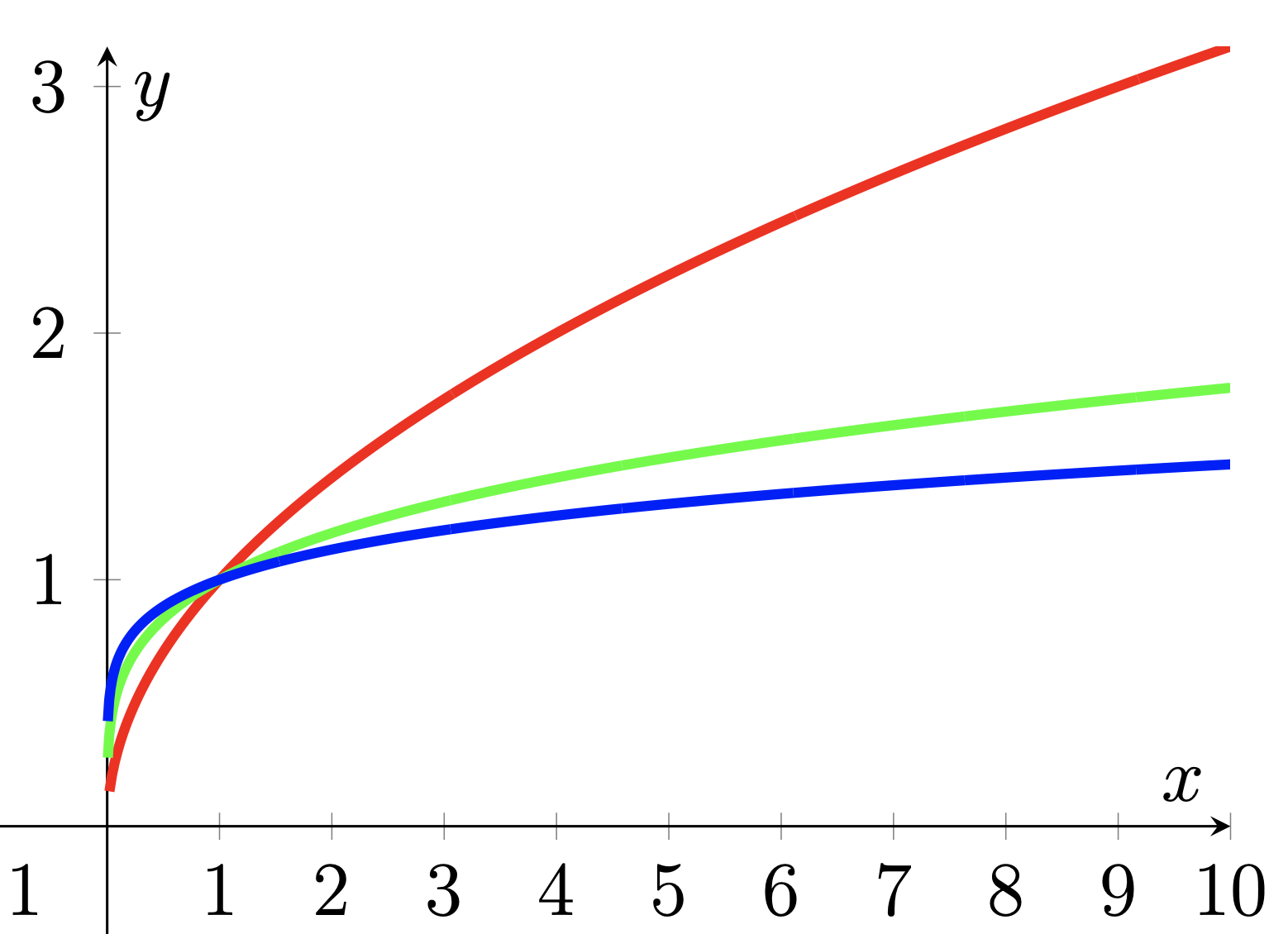
возрастает на всей ОДЗ
непрерывна на всей ОДЗ;
общего вида;

D(f) = [0; +\infty); E(f) = [0;+\infty).

(x \rightarrow +\infty \Rightarrow y \rightarrow +\infty);

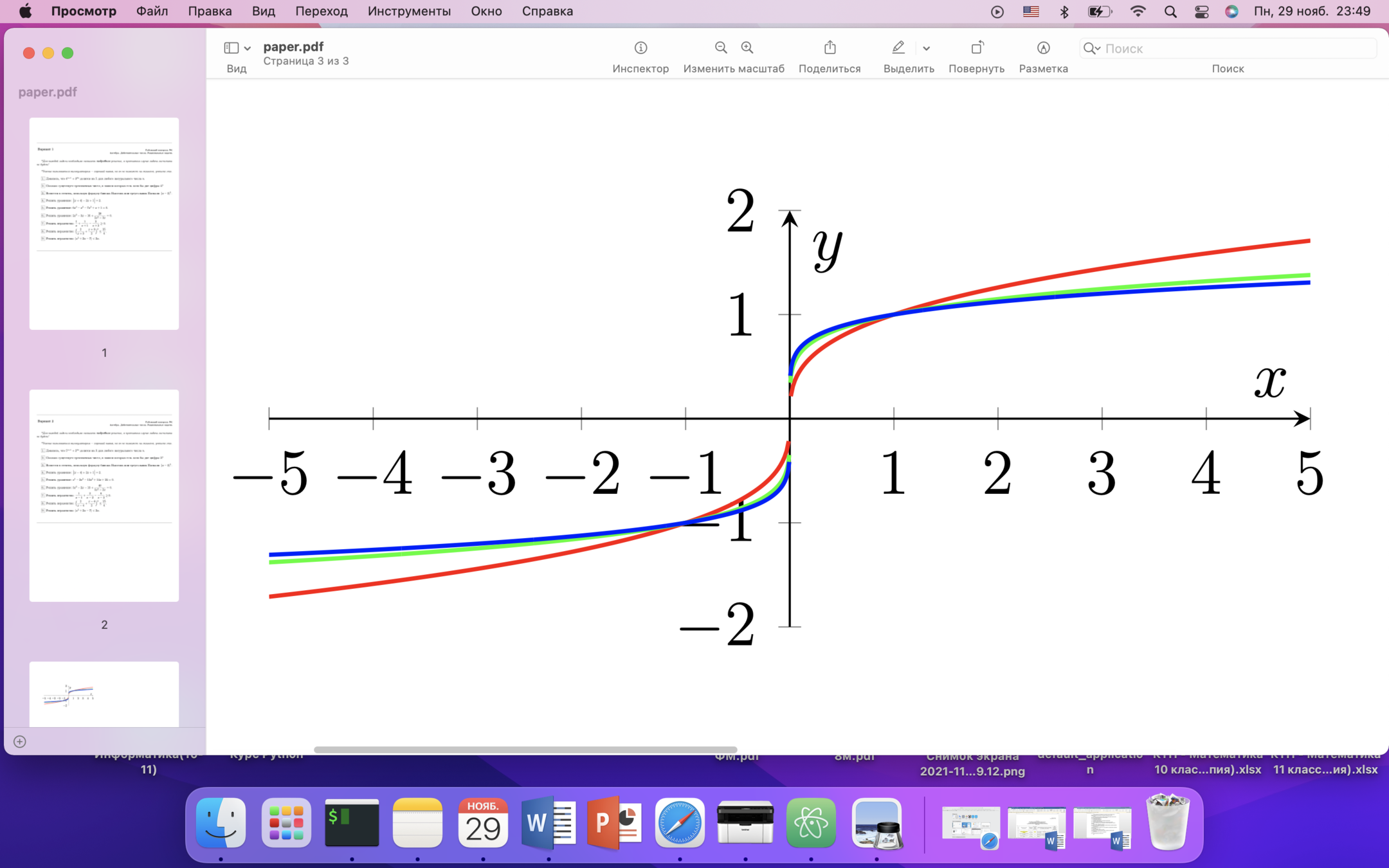
— нечетно

f(x) = \sqrt[n]{x}, n

f_3(x) = \sqrt[7]{x}

f_1(x) = \sqrt[3]{x}

f_2(x) = \sqrt[5]{x}

возрастает на всей ОДЗ
непрерывна на всей ОДЗ;
нечетная;

D(f) = \mathbb{R}; E(f) = \mathbb{R}.

(x \rightarrow +\infty \Rightarrow y \rightarrow +\infty);

Свойства арифметических корней

Для натурального числа и неотрицательных чисел , и

n (n \ge 2)

c (c \ne 0)

справедливы равенства:

\sqrt[n]{a\cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b};

\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{ \sqrt[n]{b}}.

Для любых двух действительных чисел и неотрицательных чисел и

n (n \ge 2)

a, b \ge 0

натурального числа верно утверждение:

a \le b

\sqrt[n]{a} \le \sqrt[n]{b}

Если , то .

Для любого действительного числа и натуральних чисел

a \ge 0

выполнены неравенства:

a \ge 1

\sqrt[m]{a} \le \sqrt[n]{a}

Если и , то

m, n \ge 2

m \ge n

a \le 1

\sqrt[m]{a} \ge \sqrt[n]{a}

Если и , то

m \ge n

Очень важное свойство

Для любого действительного числа и натурального числа выполнены рав-ва:

\sqrt[2k]{a^{2k}} = |a|

\sqrt[2k-1]{a^{2k-1}} = a

Задачи

1. Вычислить:

2. Вычислить:

3. Вычислить:

\sqrt[3]{1000} - \sqrt[4]{160000}

\sqrt[5]{3200000} - \sqrt[3]{8000}

\sqrt[3]{0{,}008} + \sqrt[4]{0{,}0625}

\sqrt[4]{\frac{1}{81}} + \sqrt[3]{\frac{1}{125}}

а)

б)

в)

г)

\sqrt[3]{8} - \sqrt[3]{27}

а)

\sqrt[3]{125 \cdot 27}

\sqrt[4]{16} \cdot \sqrt[4]{625}

б)

в)

\sqrt[4]{81 \cdot 16}

г)

\sqrt[3]{2} \cdot \sqrt[3]{4}

\sqrt[5]{16} \cdot \sqrt[5]{2}

д)

е)

\sqrt[4]{5} \cdot \sqrt[4]{125}

ж)

\sqrt[3]{9} \cdot \sqrt[3]{24}

\sqrt[3]{10} \cdot \sqrt[3]{100}

з)

и)

\sqrt[5]{8} \cdot \sqrt[5]{4}

\sqrt[3]{4} \cdot \sqrt[3]{16}

\sqrt[3]{4} \cdot \sqrt[3]{8} \cdot \sqrt[3]{-2}

а)

б)

в)

г)

\sqrt[5]{-7} \cdot \sqrt[5]{49} \cdot \sqrt[5]{49}

Задачи (2)

4. Найти область определения следующих функций:

y=\sqrt{8+2x-x^2}

y=\frac{\sqrt[4]{x+3}}{x-1}

y=\frac{\sqrt{x^2-1}}{4-x^2}

y=\sqrt{\frac{x^2-1}{4-x^2}}

y=\sqrt{2x^2-x} + \frac{\sqrt{9-x^2}}{x-1}

y=\sqrt{x^2(x^2-5x+6)} + \frac{1}{\sqrt{16-x^2}}

y=\frac{\sqrt{x^2-1}}{\sqrt[3]{4-x^2}}

y=\sqrt{\frac{7x^2 - 10x + 3}{7x-3} - \frac{3}{2x-3}}

а)

б)

е)

в)

г)

д)

ж)

з)

y=\sqrt[3]{x^2(x^2-5x+6)} + \frac{1}{\sqrt[7]{16-x^2}}

и)

Задачи (3)

5. Найти точку максимума функции .

y = \sqrt{4-4x-x^2}

6. Найти точку минимума функции .

y=\sqrt{x^2-6x+11}

7. Найти наибольшее значение функции .

y=\sqrt{5-4x-x^2}

8. Найти наименьшее значение функции .

y=\sqrt{x^2-8x+80}

9. Избавиться от иррациональности в знаменателе:

\frac{2}{\sqrt{5}}

\frac{3}{\sqrt{3}}

\frac{7}{\sqrt{5}}

\frac{7}{\sqrt[3]{2}}

\frac{1}{\sqrt[4]{2}}

\frac{3}{\sqrt[3]{7}}

\frac{2}{\sqrt{3} - 1}

\frac{3}{\sqrt{2} + 1}

\frac{\sqrt{3}}{\sqrt{7} + 6}

\frac{\sqrt{5}}{\sqrt{8} - 2}

а)

б)

в)

г)

д)

е)

ж)

з)

и)

к)

10. Упростить и вычислить значение выр-я: .

\sqrt{(2-\sqrt{2})^2} + \sqrt{2}

Ещё парочка свойств ...

Для натуральных чисел и неотрицательного числа

m, n (m \ge 2, n \ge 2)

справедливы равенства:

(\sqrt[n]{a})^m = \sqrt[n]{a^m};

\sqrt[nm]{a^m} = \sqrt[n]{a};

\sqrt[n]{\sqrt[m]{a}} = \sqrt[nm]{a};

Пусть — положительное число, — целое число и — натуральное

n (n\ge 2)

число. Тогда справедливо равенство:

\sqrt[n]{a^p} = (\sqrt[n]{a})^p.

FIX IT!

Задачи

1. Упростить:

2. Упростить:

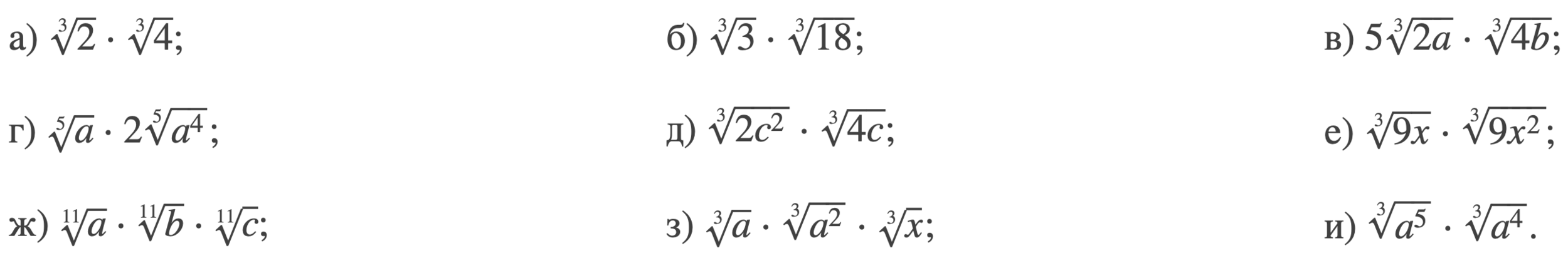
3. Упростить:

4. Упростить:

FIX IT!

Иррациональные уравнения. Равносильные переходы

\sqrt{f(x)} = g(x) \Leftrightarrow \begin{cases} f(x) = g^2(x);\\ g(x) \ge 0. \end{cases}

\sqrt{f(x)} = \sqrt{g(x)} \Leftrightarrow \begin{cases} f(x) = g(x);\\ f(x) \ge 0. \end{cases}

\begin{cases} f(x) = g(x);\\ g(x) \ge 0. \end{cases}

II.

\Leftrightarrow

k(x)\sqrt{f(x)} = 0 \Leftrightarrow \begin{cases} k(x) \cdot f(x) = 0;\\ f(x) \ge 0. \end{cases}

III.

\sqrt{f(x)} + \sqrt{g(x)} = \sqrt{k(x)} \Leftrightarrow

\Leftrightarrow \begin{cases} f(x) \ge 0;\\ g(x) \ge 0;\\ k(x) \ge 0;\\ f(x) + 2\sqrt{f(x) \cdot g(x)} + g(x) = k(x). \end{cases}

IV.

* далее приведены примеры каждого равносильного перехода

Пример I

\begin{cases} 4x^2 - \sqrt{x-1} = (4-2x)^2;\\ 4-2x \ge 0;\\ \end{cases}\\

\sqrt{4x^2 - \sqrt{x-1}} = 4-2x.

Решить уравнение:

\sqrt{4x^2 - \sqrt{x-1}} = 4-2x;\\

\begin{cases} 4x^2 - \sqrt{x-1} = 16 - 16x + 4x^2;\\ x \le 2;\\ \end{cases}\\

\begin{cases} 16(x-1) = \sqrt{x-1};\\ x \le 2;\\ \end{cases}\\

\begin{cases} \begin{cases} 16(x-1) \ge 0;\\ [16(x-1)]^2 = x - 1;\\ \end{cases}\\ x \le 2;\\ \end{cases}\\

\begin{cases} \begin{cases} x \ge 1;\\ 256(x-1)^2 = x - 1;\\ \end{cases}\\ x \le 2;\\ \end{cases}\\

\begin{cases} x \ge 1;\\ x \le 2;\\ 256(x-1)^2 = x - 1;\\ \end{cases}\\

\begin{cases} x \ge 1;\\ x \le 2;\\ (x-1)[256(x-1) - 1] = 0;\\ \end{cases}\\

\begin{cases} 1 \le x \le 2;\\ x=\left[ \begin{array}{l} 1;\\ \frac{257}{256}; \end{array} \right. \end{cases}\\

x=\left[ \begin{array}{l} 1;\\ \frac{257}{256}; \end{array} \right.

Решение:

\Rightarrow

Ответ:

1; \frac{257}{256}.

\sqrt{f(x)} = g(x) \Leftrightarrow \\ \Leftrightarrow \begin{cases} f(x) = g^2(x);\\ g(x) \ge 0. \end{cases}

Пример II

\begin{cases} 4x+2 = -x;\\ -x \ge 0;\\ \end{cases}\\

\sqrt{4x+2} = \sqrt{-x}.

Решить уравнение:

\sqrt{4x+2} = \sqrt{-x};\\

\begin{cases} x = -\frac{2}{5};\\ x \le 0;\\ \end{cases}\\

Решение:

Ответ:

-\frac{2}{5}.

\sqrt{f(x)} = \sqrt{g(x)} \Leftrightarrow \begin{cases} f(x) = g(x);\\ g(x) \ge 0. \end{cases}

\begin{cases} 5x = -2;\\ x \le 0;\\ \end{cases}\\

\Rightarrow x = -\frac{2}{5}.

Пример III

\begin{cases} (9-x^2)[2+x] = 0;\\ x+2 \ge 0;\\ \end{cases}\\

(9-x^2)\sqrt{2+x} = 0.

Решить уравнение:

(9-x^2)\sqrt{2+x} = 0.

\Rightarrow x=\left[ \begin{array}{l} -2;\\ 3. \end{array} \right.

Решение:

Ответ:

-2; 3.

k(x)\sqrt{f(x)} = 0 \Leftrightarrow \begin{cases} k(x) \cdot f(x) = 0;\\ f(x) \ge 0. \end{cases}

\begin{cases} x=\left[ \begin{array}{l} 3;\\ -3;\\ -2 \end{array} \right.\\ x \ge -2;\\ \end{cases}\\

\begin{cases} (3-x)(3+x)[2+x] = 0;\\ x+2 \ge 0;\\ \end{cases}\\

Пример IV

\begin{cases} x - 2\ge 0;\\ x-1 \ge 0;\\ 3x-5 \ge 0;\\ x-2 + 2\sqrt{(x-2)(x-1)} + (x-1) = 3x+5 \end{cases}\\

\sqrt{x-2} + \sqrt{x-1} = \sqrt{3x-5}.

Решить уравнение:

\sqrt{x-2} + \sqrt{x-1} = \sqrt{3x-5};

Решение:

\sqrt{f(x)} + \sqrt{g(x)} = \sqrt{k(x)} \Leftrightarrow \\ \Leftrightarrow \begin{cases} f(x) \ge 0;\\ g(x) \ge 0;\\ k(x) \ge 0;\\ f(x) + 2\sqrt{f(x) \cdot g(x)} + g(x) = k(x). \end{cases}

\begin{cases} x \ge 2;\\ x \ge 1;\\ x \ge \frac{5}{3};\\ 2\sqrt{x^2-3x+2} = x-2; \end{cases}\\

\begin{cases} x \ge 2;\\ 2\sqrt{x^2-3x+2} = x-2; \end{cases}\\

\begin{cases} x \ge 2;\\ \begin{cases} x \ge 2;\\ 4(x^2-3x+2) = (x-2)^2; \end{cases}\\ \end{cases}\\

\begin{cases} x \ge 2;\\ 4(x^2-3x+2) = x^2-4x+4; \end{cases}\\

\begin{cases} x \ge 2;\\ 3x^2 - 8x + 4 = 0; \end{cases}\\

\begin{cases} x=\left[ \begin{array}{l} \frac{2}{3};\\ 2; \end{array} \right.\\ x \ge 2;\\ \end{cases}\\

\Rightarrow x= 2.

Ответ:

\sqrt{f(x)} = g(x) \Leftrightarrow \\ \Leftrightarrow \begin{cases} f(x) = g^2(x);\\ g(x) \ge 0. \end{cases}

FIX IT!

Задачи

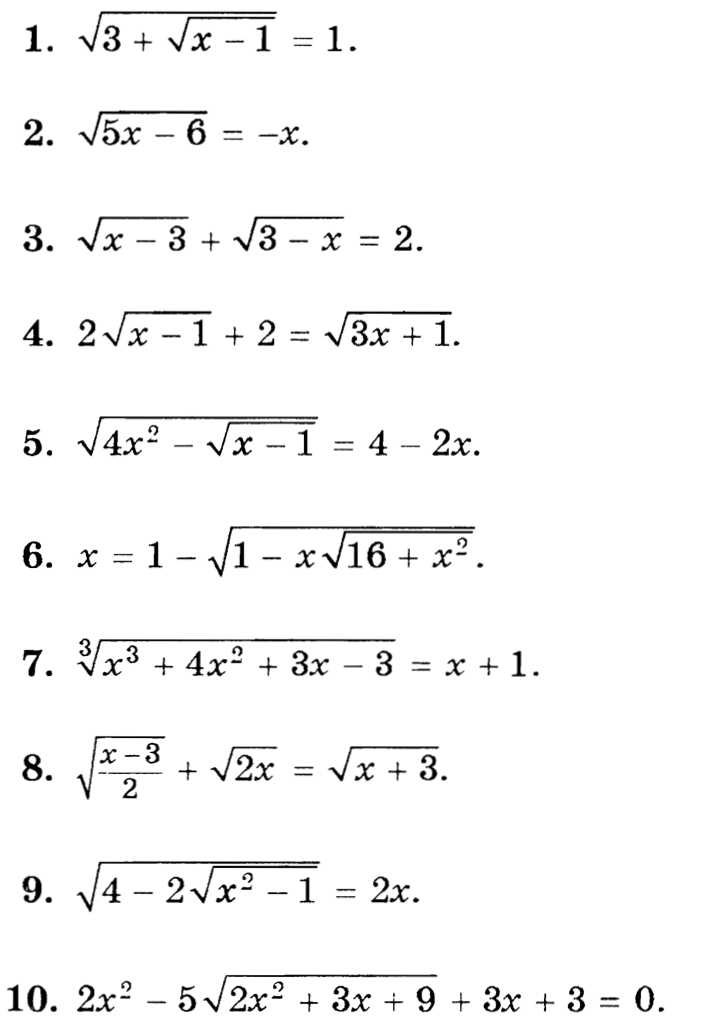
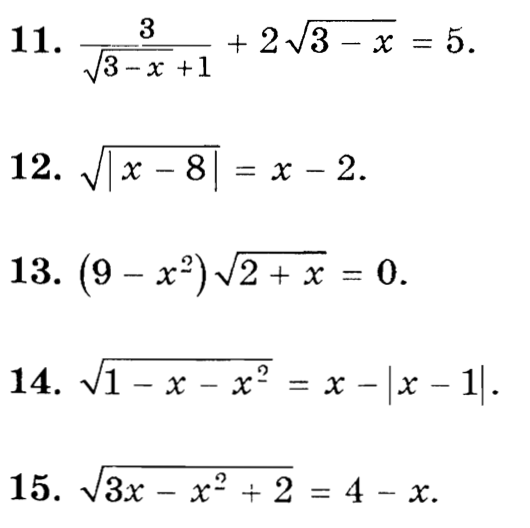
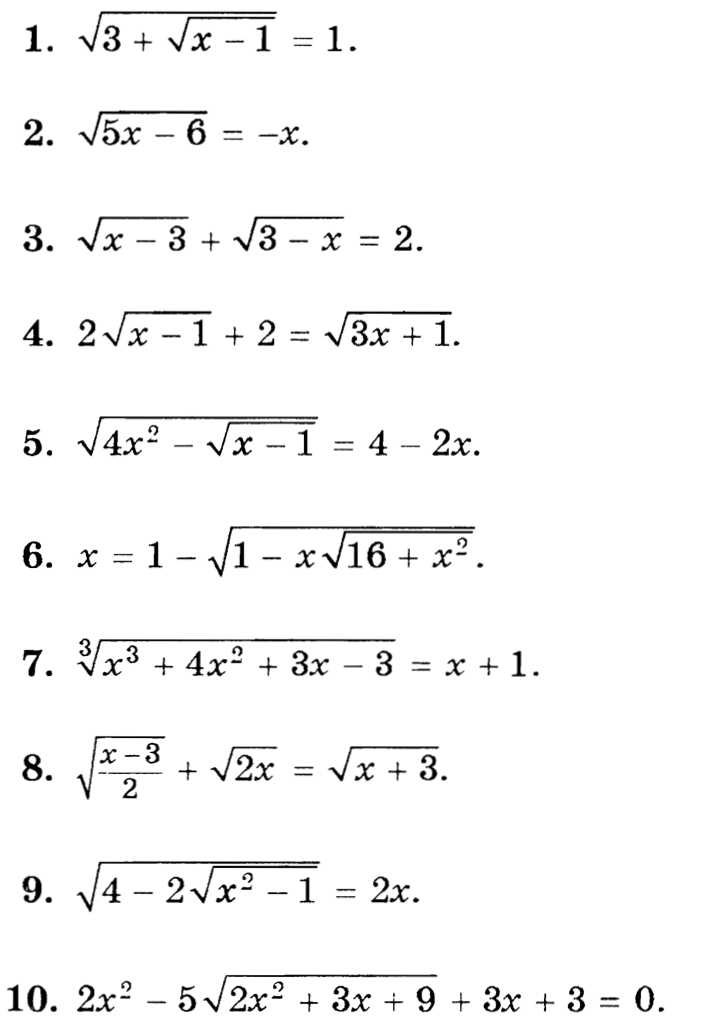
Иррациональные неравенства. Равносильные переходы

\sqrt{f(x)} < _{\le} g(x) \Leftrightarrow \begin{cases} g(x) \ge 0;\\ f(x) \ge 0;\\ f(x) <_{\le} g^2(x). \end{cases}

I(a).

I(b).

k(x)\sqrt{f(x)} \vee 0 \Leftrightarrow \begin{cases} k(x) \cdot f^2(x) \vee 0;\\ f(x) \ge 0. \end{cases}

II.

\sqrt{f(x)} + \sqrt{g(x)} \vee \sqrt{k(x)} \Leftrightarrow

\Leftrightarrow \begin{cases} f(x) \ge 0;\\ g(x) \ge 0;\\ k(x) \ge 0;\\ f(x) + 2\sqrt{f(x) \cdot g(x)} + g(x) \vee k(x). \end{cases}

IV.

\sqrt{f(x)} >_{\ge} g(x) \Leftrightarrow \left[ \begin{array}{l} \begin{cases} g(x) \ge 0;\\ f(x) >_{\ge} g^2(x);\\ \end{cases}\\ \begin{cases} g(x) < 0;\\ f(x) \ge 0.\\ \end{cases} \end{array} \right.

III(a).

\sqrt{f(x)} >_{\ge} \sqrt{g(x)} \Leftrightarrow \begin{cases} g(x) \ge 0;\\ f(x) >_{\ge} g(x). \end{cases}

III(b).

\sqrt{f(x)} <_{\le} \sqrt{g(x)} \Leftrightarrow \begin{cases} f(x) \ge 0;\\ f(x) <_{\le} g(x). \end{cases}

Задачи

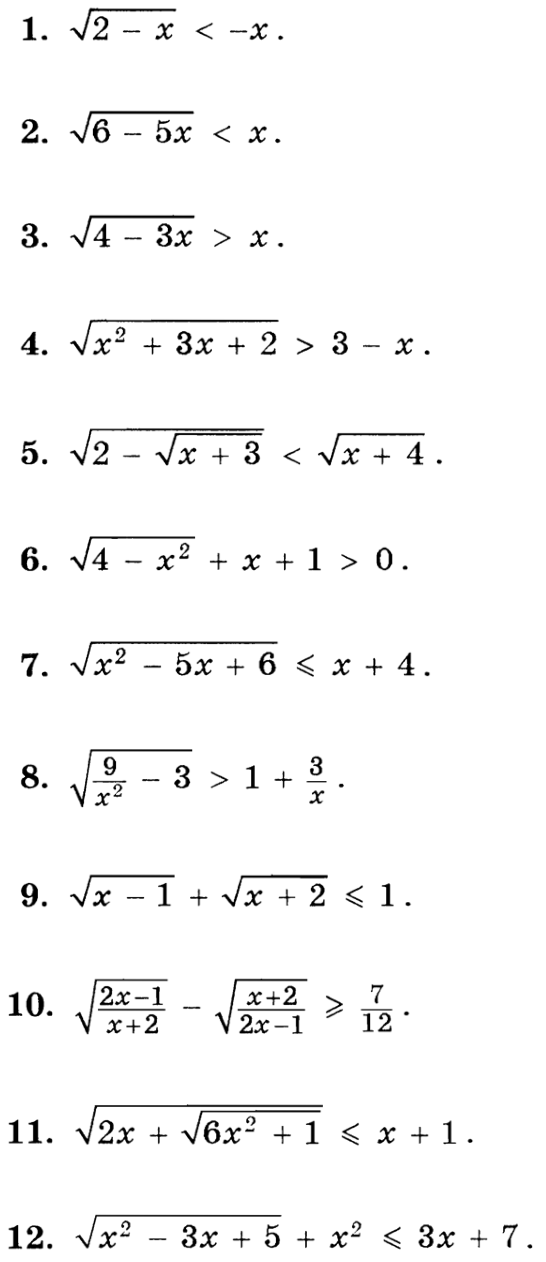
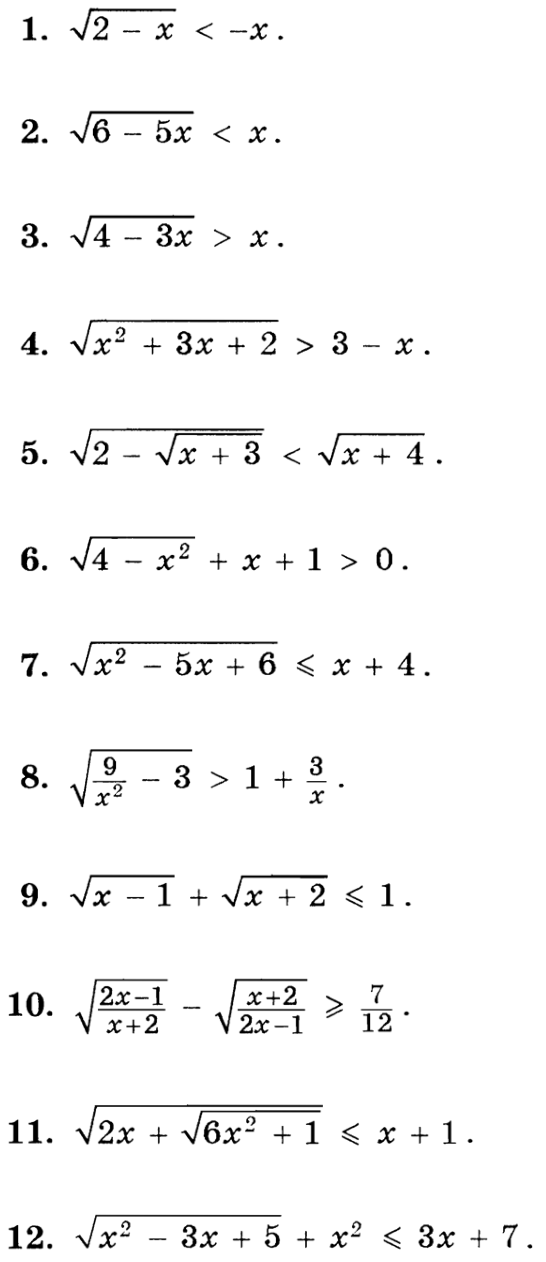
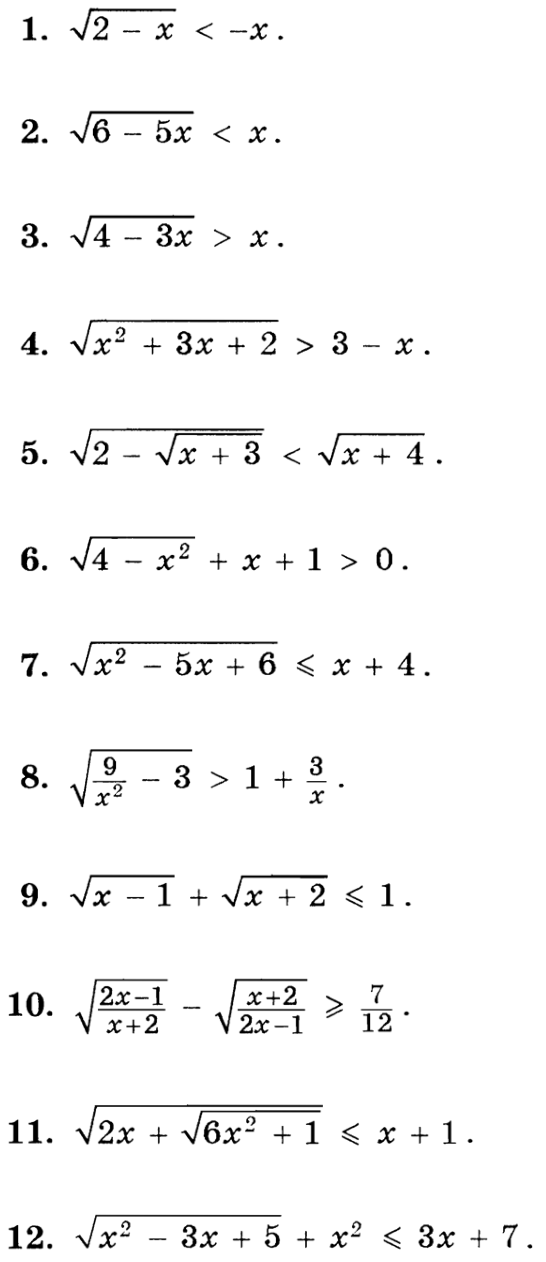
Степень с рациональным показателем

Пусть — положительное число, а — рациональное число ( ). По определению число в степени есть арифметический корень степени из в степени :

\frac{p}{q}

q \ge 2

\frac{p}{q}

a^\frac{p}{q} = \sqrt[q]{a^p}

Если — положительное число, — целое, — натуральные числа (больше или равные двум), тогда справедливы равенства:

k, q

a^\frac{p}{q} = (a^\frac{1}{q})^p

a^\frac{p}{q} = a^\frac{p \cdot k}{q \cdot k}

a^p = a^\frac{p \cdot k}{k}

Свойства степени с рациональным показателем

Теорема 1: Положительное число в степени с любым рациональным показателем положительно:

a^r > 0

Теорема 3: Пусть — положительные числа, a — рациональное число. Тогда справедливы свойства:

a, b

a^{r_1} \cdot a^{r_2} = a^{r_1 + r_2}

a^{r_1} : a^{r_2} = a^{r_1 - r_2}

(a^{r_1})^{r_2} = a^{r_1 \cdot r_2}

a^{-r} = \frac{1}{a^{r}}

Теорема 2: Пусть — положительное число, a , и — рациональные числа. Тогда справедливы свойства:

r_1

r_2

(ab)^r = a^r \cdot b^r

(\frac{a}{b})^r = \frac{a^r}{b^r}

Задачи

1. Вычислить