Теория информации

10 класс

vkrysanov320@gmail.com

Что такое информация?

Термин «информация» происходит от латинского слова «informatio», что означает разъяснение, изложение, осведомлённость

Кодирование информации — это переход от одной формы представления информации к другой, более удобной для восприятия, обработки, хранения и передачи.

Представление информации на ЭВМ

Графическая

Звуковая

Текстовая

Видео

Числовая

Оценка количества информации

Бит — базовая единица измерения количества информации, равная количеству информации, содержащемуся в опыте, имеющем два равновероятных исхода

Единицы измерения информации

1 байт	= 8 бит
1 килобайт (Кб)	= 1024 байт
1 мегабайт (Мб)	= 1024 килобайта
1 гигабайт (Гб)	= 1024 мегабайта
1 терабайт (Тб)	= 1024 гигабайта


1 килобит (Кбит)	= 1024 бита
1 мегабит (Мбит)	= 1024 килобита
1 гигабит (Гбит)	= 1024 мегабита
1 терабит (Тбит)	= 1024 гигабита

:1024

\cdot 8

\cdot 1024

Задачи

1. В одной из кодировок Unicode каждый символ кодируется 16 битами. Определить размер следующего предложения в данной кодировке:

Роняет лес багряный свой убор, сребрит мороз увянувшее поле.

2. Статья, набранная на компьютере, содержит 16 страниц, на каждой странице 30 строк, в каждой строке 32 символа. Определить информационный объём статьи в одной из кодировок Unicode, в которой каждый символ кодируется 16 битами.

Представление числовой информации на ЭВМ

Для хранения чисел в памяти компьютера используется два формата:

целочисленный;
с плавающей точкой.

Прямой код

Знаковый разряд

Цифровые разряды

При этом, если:
— знаковый разряд равен 0, то число положительное;
— знаковый разряд равен 1, то число отрицательное.

1	1	0	1	0	0	0	1

Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел

= - \sum\limits_{i = 0}^{n} a_i \cdot 2^i = - 81;

0	1	0	1	0	0	0	1

= \sum\limits_{i = 0}^{n} a_i \cdot 2^i = 81.

Прямой код. Примеры

1	0	0	0	0	0	0	0

0	0	0	0	0	0	0	0

— «Отрицательный ноль»

— «Положительный ноль»

1	0	0	0	0	1	0	1

= - (2^{-5} + 2^{-7}) = -\frac{5}{128}

0	0	0	0	0	1	0	1

= 2^{0} + 2^{2} = 5

Неудобно!

При использовании для чисел со знаком у прямого кода есть два недостатка.

В прямом коде есть два варианта записи числа 0 (положительный и отрицательный ноль);
Формальное суммирование чисел с различающимися знаками даёт неверный результат, а процедура для корректного сложения чисел в прямом коде очень громоздка.

Обратный код

1	1	0	1	0	0	0	1

Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами.

Правило образования. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы нулями:

1	0	1	0	1	1	1	0

0	1	0	1	0	0	0	1

0	1	0	1	0	0	0	1

\text{ОК}

\text{П}

\text{ОК}

Зачем?

Упрощает арифметику с отрицательными числами.

Вычислить в обратном коде

64 + (-31)

64 = 0 | 1000000_{\text{П}} = 0 | 1000000_{\text{OK}}

-31 = 1 | 0011111_{\text{П}} = 1| 1100000_{\text{ОК}}

\Rightarrow 0|0100001_{\text{ОК}} = 0|0100001_{\text{П}} = 2^0 + 2^5 = 33.

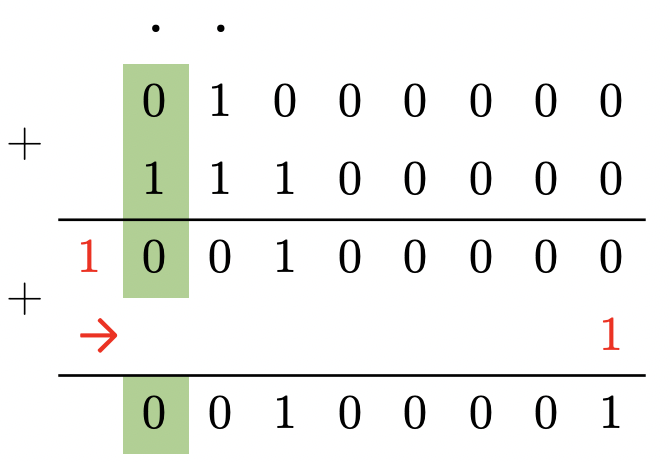
Опять неудобно!

процесс суммирования чисел является двухэтапным, что увеличивает время выполнения этой операции;
как и в прямом коде, в обратном — два представления нуля.

Дополнительный код

1	1	0	1	0	0	0	1

Обратный код — позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.

Правило образования: Обратный код положительных чисел совпадает с их допонительным кодом. А если число отрицательное, то все разряды числа, кроме знакового, инвертируются, а к результату прибавляется 1.

1	0	1	0	1	1	1	0

0	1	0	1	0	0	0	1

0	1	0	1	0	0	0	1

\text{ДК}

\text{П}

\text{ОК}

\text{ДК}

1	0	1	0	1	1	1	1

Вычислить в дополнительном коде

64 + (-31)

64 = 0 | 1000000_{\text{П}} = 0 | 1000000_{\text{OK}} = 0|1000000_{\text{ДК}}

-31 = 1 | 0011111_{\text{П}} = 1| 1100000_{\text{OK}} = 1| 1100001_{\text{ДК}}

\Rightarrow 0|0100001_\text{ДК} = 0|0100001_\text{П} = 2^0 + 2^5 = 33.

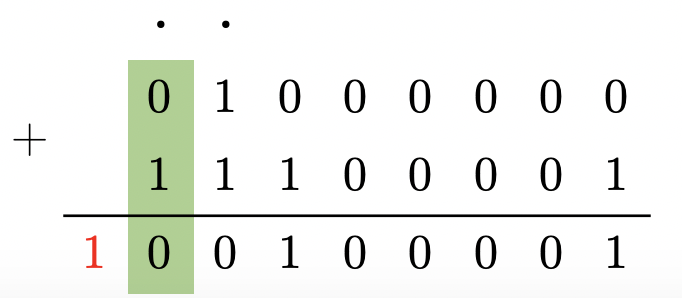
Диапазон представления беззнаковых целых чисел

n\text{-бит}:

[0; 2^{n}-1]

[0; 1-(2^{n}-1)]

-разрядный код ( цифровых разрядов) позволяет представлять:

целые числа в диапазоне:

правильные двоичные дроби в диапазоне:

...

Диапазон представления знаковых целых чисел

n-1

n\text{-бит}:

[-2^{n-1}; 2^{n-1}-1]

[-1-(2^{-n-1}); 1-(2^{n-1}-1)]

-разрядный код ( цифровых разрядов и один знаковый) позволяет представлять:

n-1

целые числа в диапазоне:

правильные двоичные дроби в диапазоне:

...

Задачи

long int

1. В языке программирования С, целые знаковые числа можно представить типом , переменная, которого занимает 8 байт. Какой диапазон чисел можно представить данным типом?

unsigned int

2. В языке программирования С, целые беззнаковые числа можно представить типом , переменная, которого занимает 8 байт. Какой диапазон чисел можно представить данным типом?

Представление графической информации на ЭВМ

Существуют два принципа представления изображения на компьютере:

векторный;
растровый.

Векторная графика

Векторная графика — способ представления объектов и изображений (формат описания) в компьютерной графике, основанный на математическом описании элементарных геометрических объектов, обычно называемых примитивами, таких как: точки, линии, сплайны, кривые Безье, круги и окружности, многоугольники.

SVG, EMF, CDR, CGM, DXF, OpenVG, GXL, WMF, EPS, PDF, AI, SWF, SWFTools, DXE, FLA, ...

Форматы:

<svg height="499pt"
     viewBox="0 -9 499.20714 499"
     width="499pt"
     xmlns="http://www.w3.org/2000/svg">
	<polyline points="0,0 50,0 150,100 250,100 300,150"
              fill="rgb(249,249,249)"
              stroke-width="1"
              stroke="rgb(0,0,0)"/>
</svg>

\Downarrow

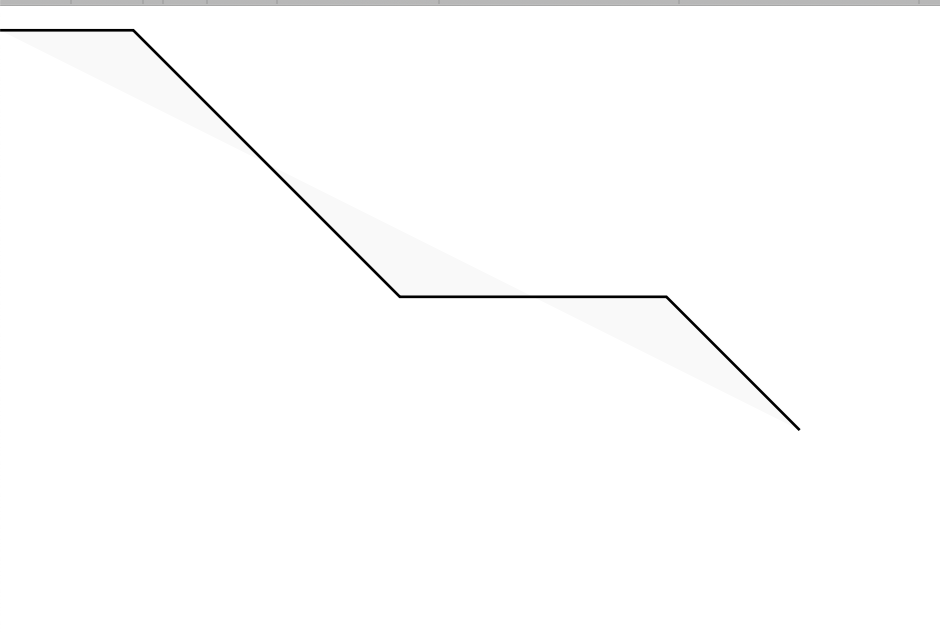
Кодирование векторного изображения

The Art of Computer Programming

Дональд Кнут

Где используется?

Векторная графика используется там, где необходимо обеспечить «безболезненную» масштабируемость изображений и малый размер файлов.

Чаще всего векторная графика используется для создания макетов, наиболее распространена в полиграфическом дизайне. Векторная графика не может передать тона и полутона, но гораздо более удобна если речь идет о простых формах, текстах, контурных фигур.

Достоинства и недостатки

Векторное изображения можно легко масштабировано без потери качества.
Графические файлы имеют существенно меньший, по сравнению с растровым объём.
Максимально использует разрешающие возможности устройства вывода.

qТрудно получить фотореалистичное изображение.
При прорисовке необходимо каждый раз раqстеризовать изображение.
Программная зависимость вследствие отсутствия единого формата.

Достоинства

Недостатки

Вычисление объёма векторного изображения

В векторной графике объем памяти, занимаемый линией (контуром), не зависит от размеров линии, поскольку линия представляется в виде формулы, а точнее говоря, в виде нескольких параметров.

Фрактальная графика

Фрактальная графика, как и векторная, основана на математических вычислениях. Однако базовым элементом фрактальной графики является сама математическая формула, т.е. никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям.

Фрактал — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей).

Множество Мандельброта

Множество Жюлиа

Ещё фракталы ...

Где применяются?

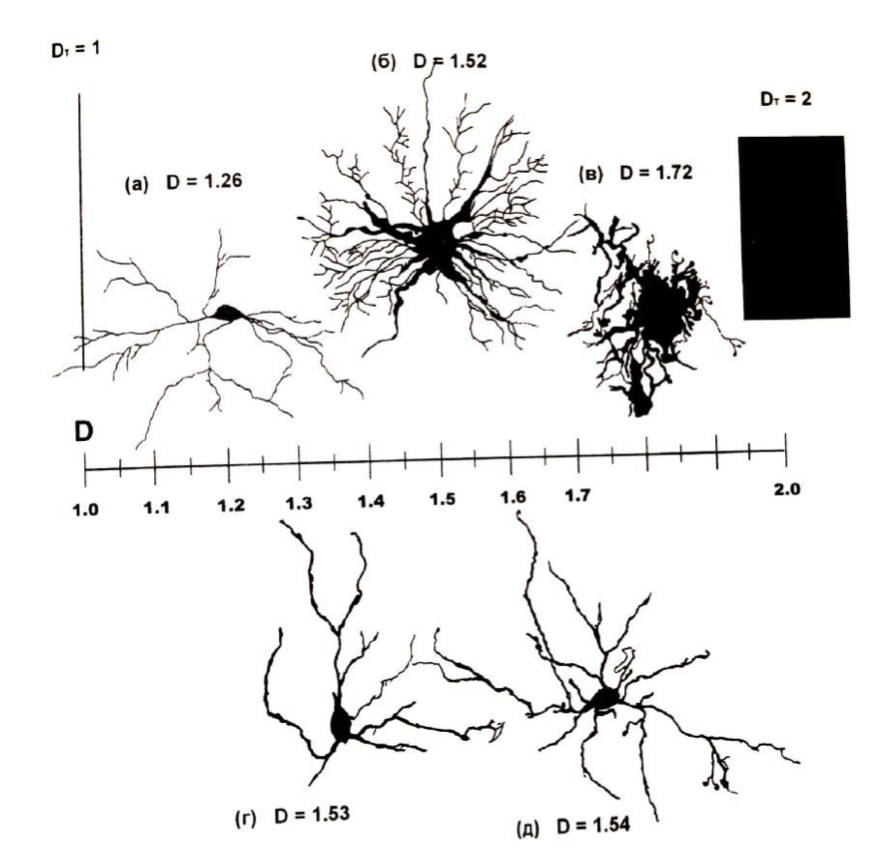
Биология и медицина

Для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов);
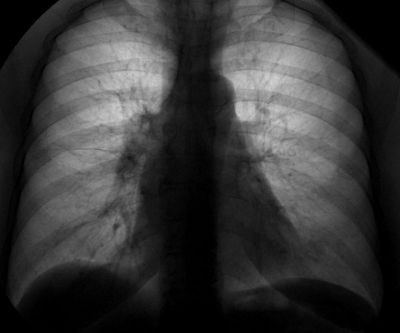
Рентгеновские снимки обработанные с помощью фрактальных алгоритмов дают более качественную картинку а соответственно и более качественную диагностику.
Карты адгезии (в физике — сцепление поверхностей разнородных твёрдых и/или жидких тел) поверхностей нормальных и раковых клеток имею разную фрактальную размерность.

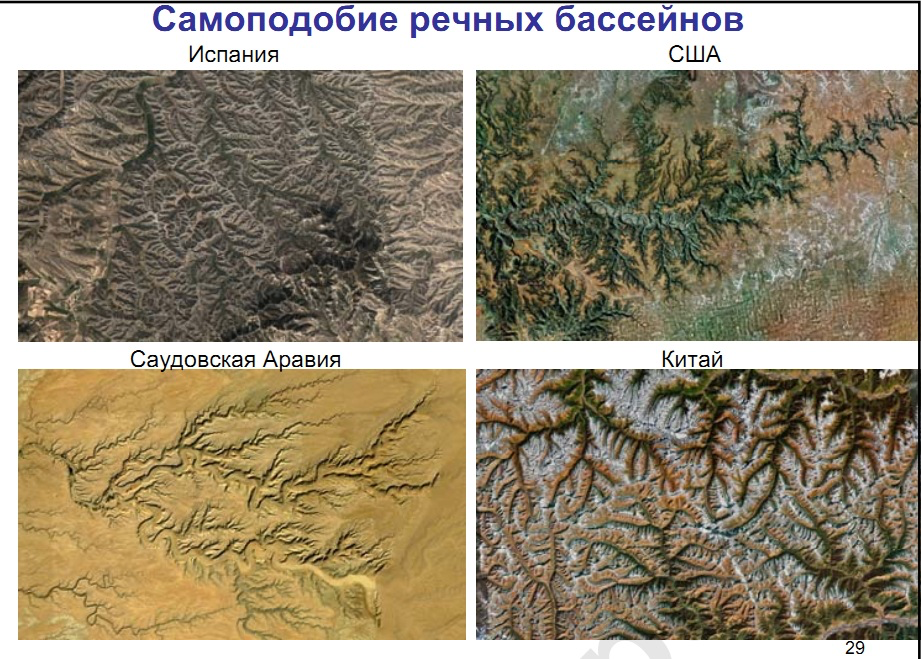
Геология и геофизика

Побережья островов и континентов имеют некоторую фрактальную размерность, зная которую можно очень точно вычислить длины побережий.
Фрактальный анализ помогает в поиске и разработке месторождений полезных ископаемых, распределение которых очень часто происходит по фрактальному механизму.

Физика, информатика

Сжатие изображений с помощью фракталов. Построение изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее.
В телекоммуникациях фракталы используются для создания фрактальных антенн.
Изучение турбулентности в потоках очень хорошо подстраивается под фракталы.

Растровая графика

Растровое изображение — изображение, представляющее собой сетку пикселей — цветных точек (обычно прямоугольных) на мониторе, бумаге и других отображающих устройствах.

BMP, TIFF, GIF, JPEG, PNG, PSD, ICO, ...

Форматы:

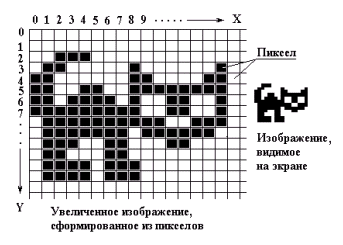
Пиксель:

наименьший элемент двумерного цифрового изображения в растровой графике;
«физический» элемент матрицы дисплеев, формирующих изображение.

Кодирование растрового изображения

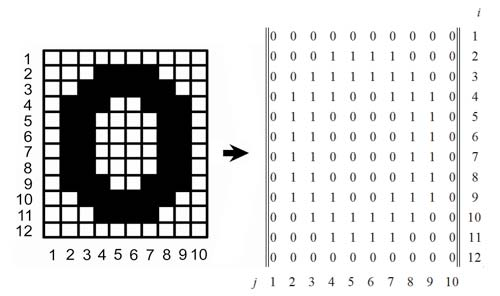
Два цвета (чёрный — 1, белый — 0):

bitmap

Какие существуют характеристики растрового изображения?

(1) Размер изображения в пикселях

Может выражаться в виде количества пикселей по ширине и по высоте ( px, px,

px и т.п.) или же в виде общего количества пикселей.

800\text{x}600

1024\text{x}768

1600\text{x}1200

(2) Глубина цвета

Количество используемых цветов или глубина цвета (эти характеристики имеют следующую зависимость: , где — количество цветов, — глубина цвета);

N = 2^{k}

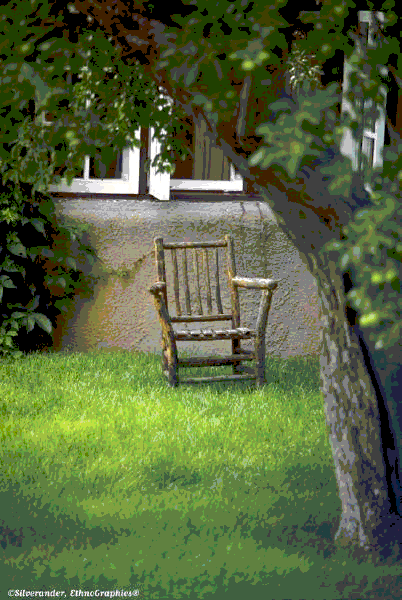
4 bit

16 bit

(3) Цветовое пространство

RGB

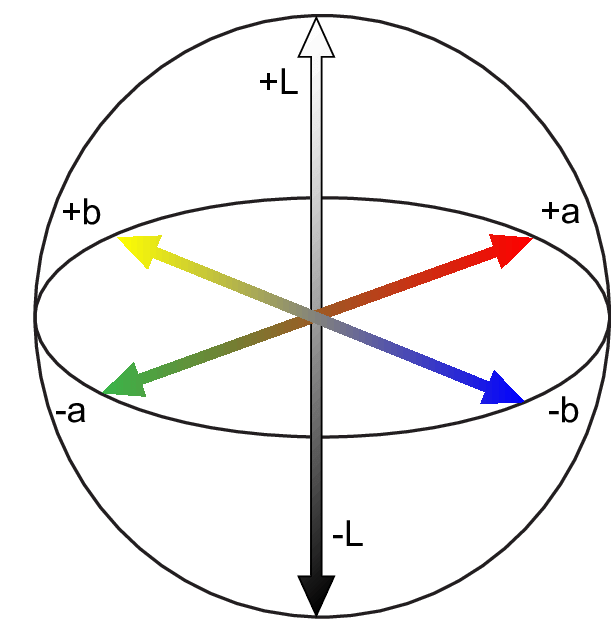
Lab

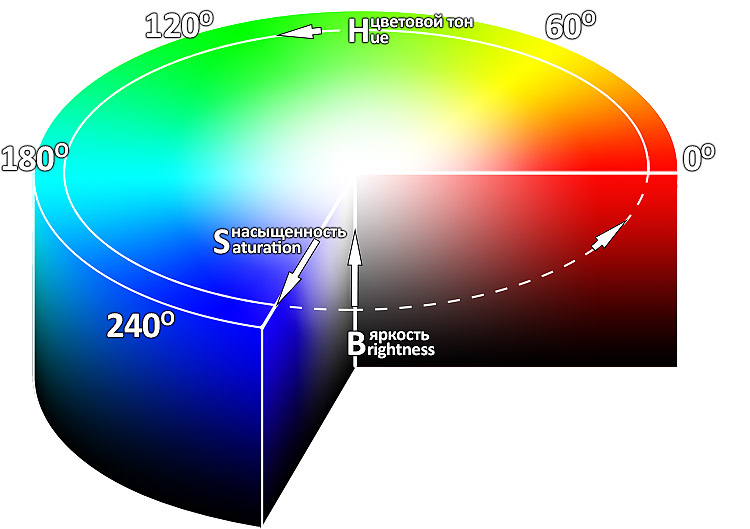
Hsb

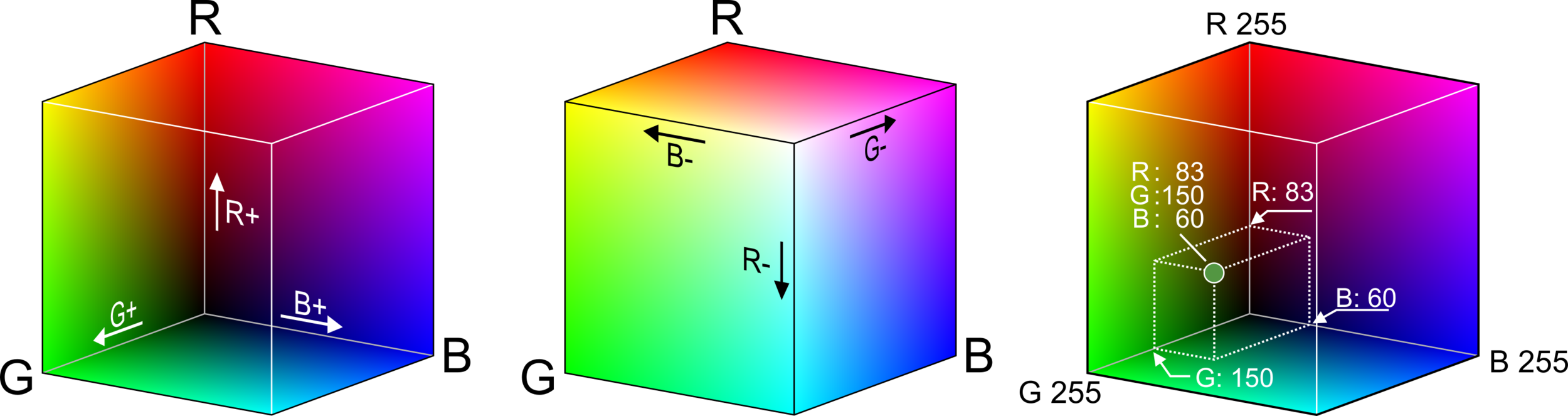
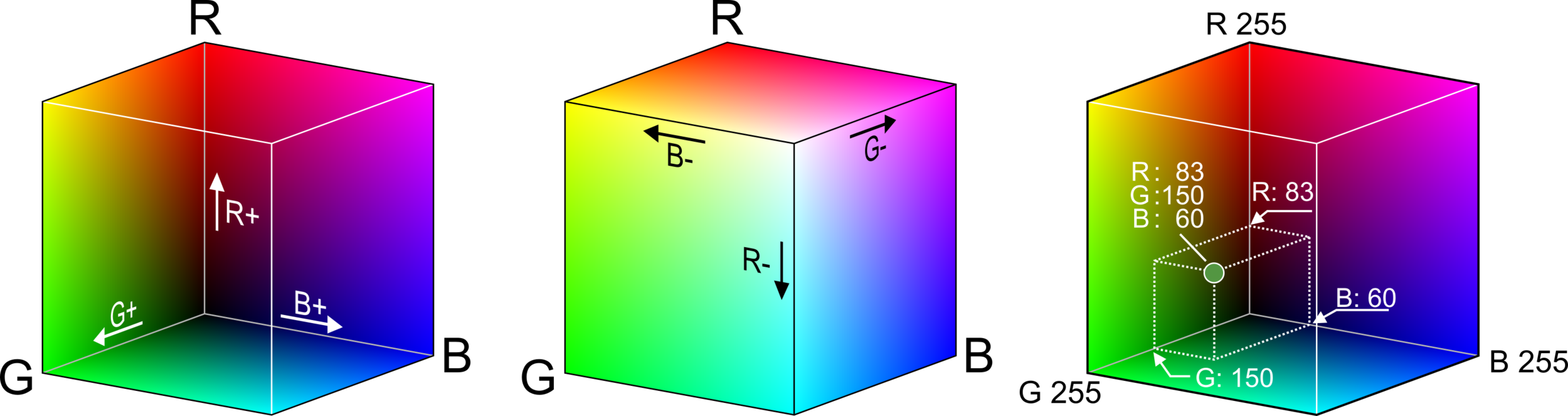
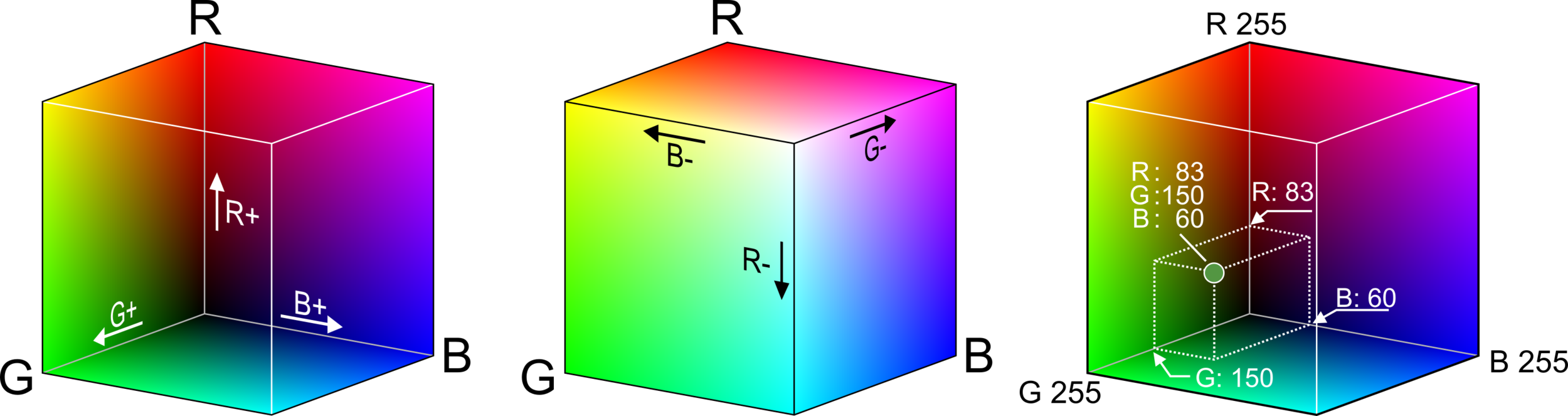
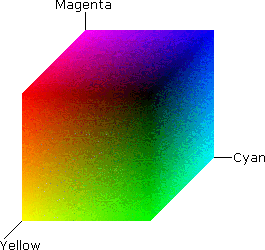
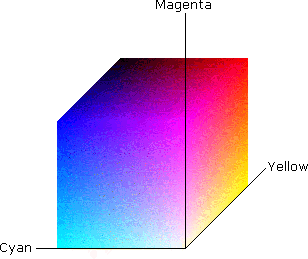
CMY

Где используется?

На любом дисплее информация отображается именно в растровом виде.

Достоинства растровой графики

Возможность воспроизведения изображений любого уровня сложности. Количество деталей, воспроизводимых на изображении во многом зависит от количества пикселов.
Точная передача цветовых переходов.
Наличие множества программ для отображения и редактирования растровой графики.

Большой размер файла. Фактически для каждого пиксела приходится хранить информацию о его координатах и цвете.
Невозможность масштабирования (в частности, увеличения) изображения без потери качества.

Достоинства

Недостатки

Вычисление объёма растрового изображения

V = K \cdot I

— объем файла, — количество пикселей изображения,

— глубина

N = 2^I; I = \lceil \log_2{N} \rceil

— количество цветов, — глубина

Объём

Глубина

1. Вычислить объем растрового изображения размером и палитрой цветов.

2. Какой минимальный объём памяти (в Кбайт) необходимо зарезервировать, чтобы можно было сохранить любое растровое изображение размером пикселей при условии, что в изображении могут использоваться различных цветов?

3. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером пикселов при условии, что в изображении могут использоваться различных цветов?

Задачи

128\text{x}128

256

128\text{x}128

512

512\text{x}512

256

4. Автоматическая фотокамера производит растровые изображения размером пикселей. При этом объём файла с изображением не может превышать Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?

5. Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей цветов. Средний размер фотографии составляет Мбайт. Для хранения в базе данных фотографии преобразуют в чёрно-белый формат с палитрой, содержащей цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?

Задачи (2)

800\text{x}600

600

2^{24} = 16'777'216

256

Разрешение — величина, определяющая количество точек (элементов растрового изображения) на единицу площади (или единицу длины).

Разрешение

	Экранное	Принтер	Сканер
Измеряется	px	dpi (англ. dots per inch) — количество точек на дюйм	ppi (англ. point per inch) — количество пикселей на дюйм
Зависит	от монитора, видеокарты, настроек ОС	от количества точек, которые могут напечатаны на участке единичной длины	от количества точек, которые светочувствительные датчики могут считать с каждой горизонтальной полосы изображения
Определяет	размер изображения, которое может поместиться на экране целиком	качество изображения в заданном размере	качество изображения (увеличение изображения бюез потери качества)

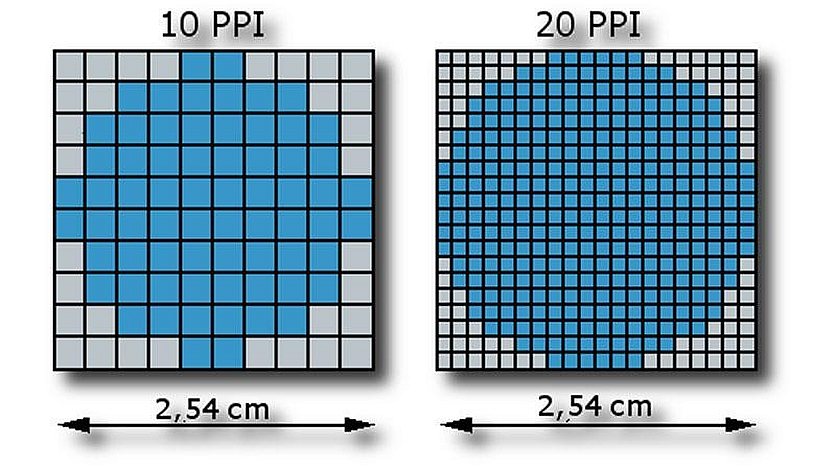
Задачи

1. Для хранения в информационной системе документы сканируются с разрешением dpi и цветовой системой, содержащей цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет Мбайт. В целях экономии было решено перейти на разрешение dpi и цветовую систему, содержащую цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?

2^{24}

600

300

2^{16}

Представление звуковой информации на ЭВМ

Что такое звук?

Звук (в узком смысле) — волнообразно распространяющееся колебательное движение материальных частиц упругой среды, воспринимаемое органами слуха.

f(\tau)

\tau

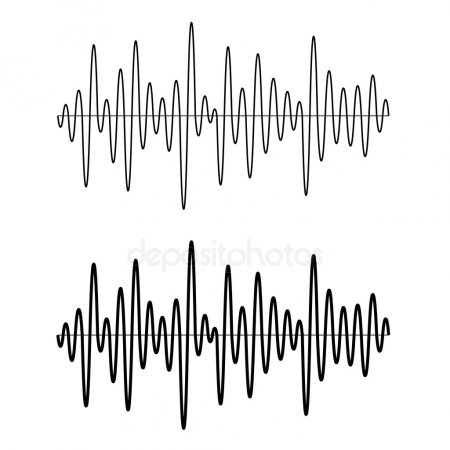
Аналоговый звук представляется в аппаратуре непрерывным электрическим сигналом.

f(\tau)

\tau

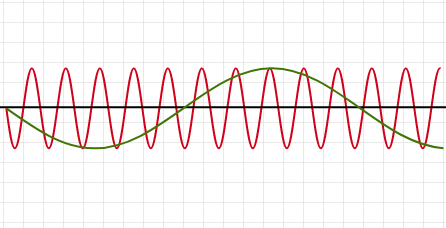
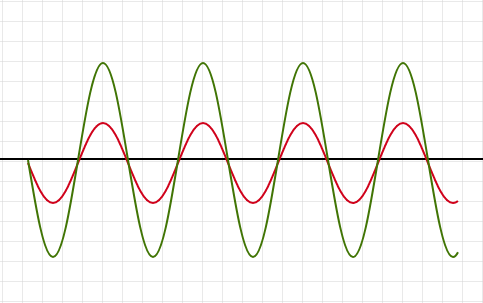
Волны чаще — звук выше

Амплитуда больше — громче звук

Сколько значений содержится, к примеру, в диапазоне от до у ?

f(x) = \sin(x)

\frac{\pi}{2}

\pi

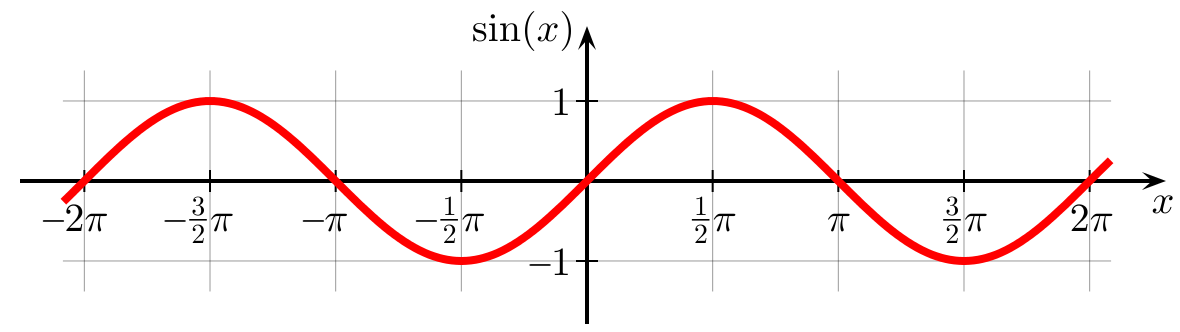
Как звук представить в памяти компьютера?

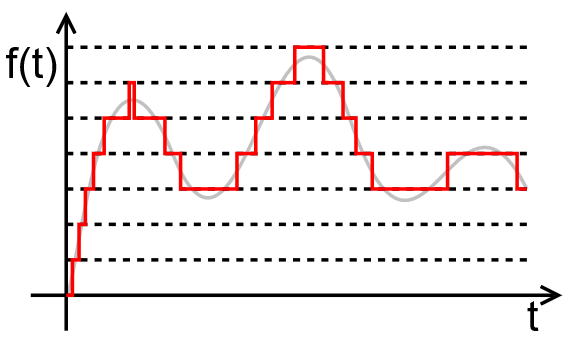
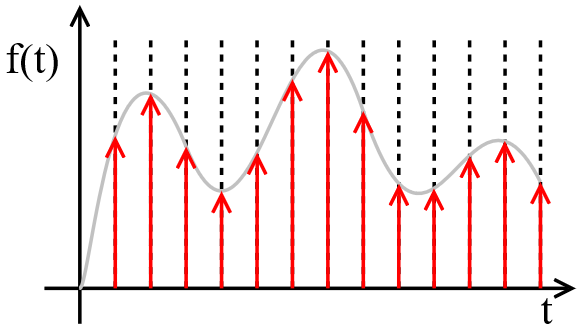
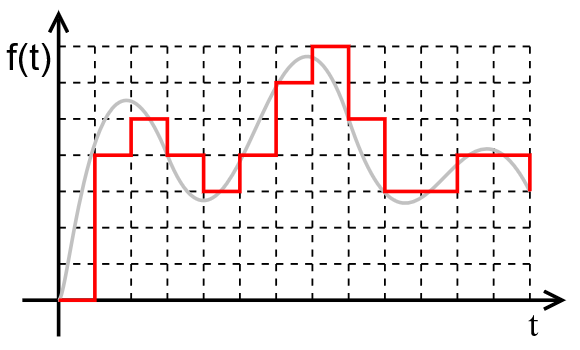
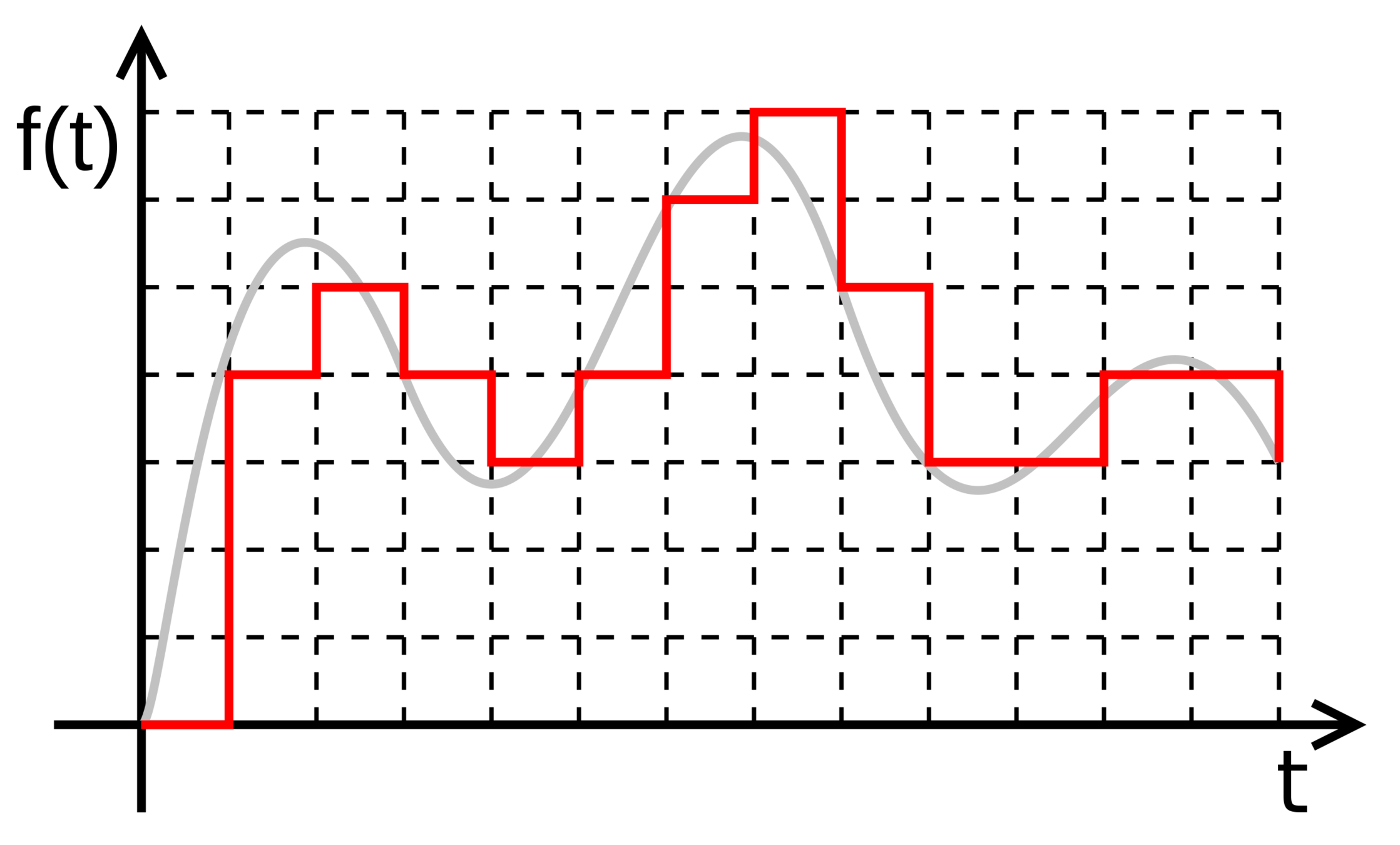
Квантование и дискретизация

\tau

f(\tau)

Есть две основные характеристики цифрового сигнала — частота дискретизации и глубина дискретизации по уровню.

Процесс преобразования непрерывного аналогового сигнала в цифровой сигнал называется дискретизацией (по времени и по уровню).

Цифровой сигнал — это набор значений уровня сигнала, записанный через заданные промежутки времени.

«Звуковая перспектива»

f(\tau)

f_1(\tau), f_2(\tau), ... f_n(\tau)

f_1(\tau), f_2(\tau)

\tau

Монозвук

Стереозвук

Многоканальный звук

Информационный объём аудиофайла

V = T \cdot f \cdot I \cdot k

— объем файла, — общая длительность звучания (с),

— частота дискретизации (Гц), — глубина кодирования (бит)

— количество каналов

N = 2^I; I = \lceil \log_2{N} \rceil

— количество уровней дискретизации

— глубина дискретизации

Объём

Глубина

Задачи

1. Оценить информационный объём цифрового стереозвукового файла длительностью звучания секунда при среднем качестве звука ( бит, измерений в секунду).

2. Вычислить глубину кодирования звука, если частота дискретизации — кГц, время звучания — секунд, объём файла Кбайт, звукозапись — одноканальная.

3. Производилась стерео звукозапись с частотой дискретизации кГц и -битным разрешением. В результате был получен файл размером Мбайт. Определить приблизительно, сколько времени (в минутах) проводилась запись. Ответ округлить до целых.

624000

320

20625

Представление видеоинформации

Видеоинформация — это прежде всего, это сочетание звуковой и графической информации. Для создания на экране эффекта движения используется технология быстрой смены статических картинок.

Если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные.

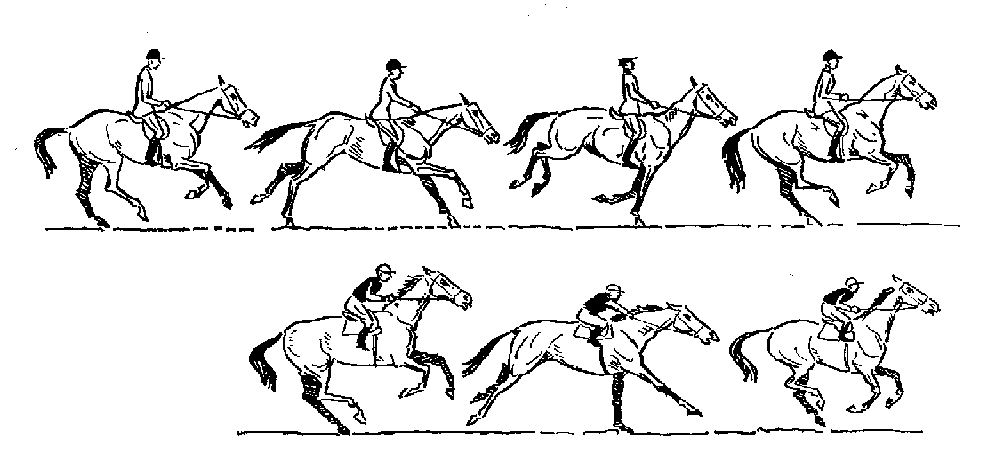
1	2	3	4	5	6	7

Некоторая проблемка...

Видеофайл — это набор статичных изображений, меняющих друг друга с определенной частотой. Каждое статичное изображение является отдельным кадром видео. Однако в таком формате никто не хранит фильмы. Почему?

Некоторая проблемка...

К примеру, кадр видео формата PAL состоит из точек.

Для хранения цвета каждой точки в памяти отводится 24 бита.

Несжатое видео занимает на диске очень много места!

720\text{x}576

\Rightarrow

для хранения одного кадра понадобится 9953280 бит (или примерно 1,2 Мбайт).
секунда несжатого видео в формате PAL будет занимать почти 30 Мбайт.
час такого видео — более 100Гбайт.

Решение проблемы

В основном, видео хранят в видеофайлах, в которых применены различные алгоритмы сжатия информации. Благодаря этим технологиям видеофайл можно сжимать в десятки и сотни раз практически без потери качества картинки и звука.

Кодирование цвета

Перевод изображения в цветовое пространство YUV. Яркостная компонента (Y) содержит «черно-белое» (в оттенках серого) изображение, а оставшиеся две компоненты содержат информацию для восстановления требуемого цвета.

Компенсация движения

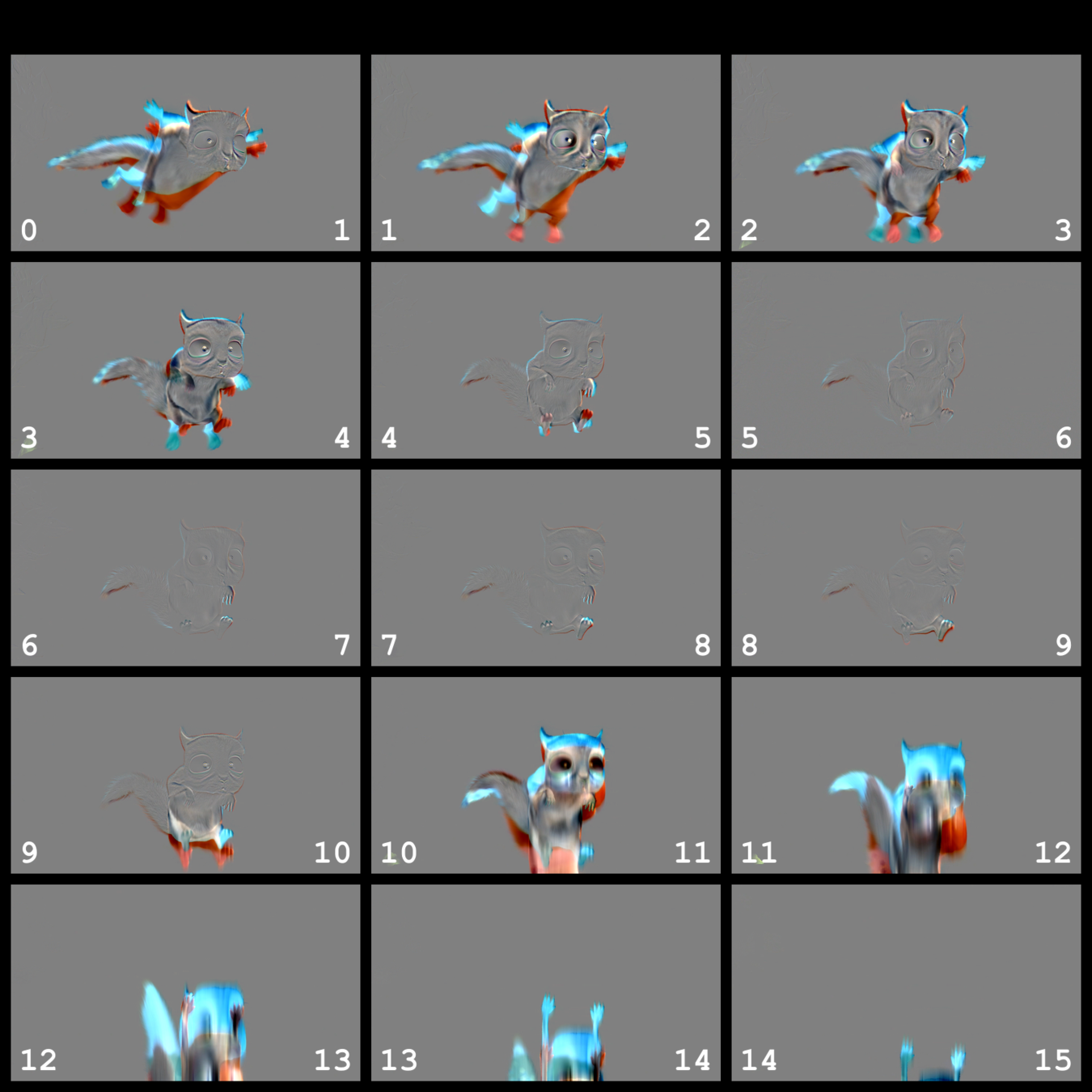
Изображение делится на блоки и в окрестности каждого из них ищется похожий блок на другом кадре (motion estimation), так получается поле векторов движения. А уже при компенсации (motion compensation) учитываются вектора движения, и создается изображение в целом похожее на исходный кадр:

Применение различных алгоритмов сжатия изображений

Что такое информация?

Сколько вопросов необходимо задать, чтобы найти задуманное число

от 1 до 100?

Подсказка

Есть такой способ поиска, как «деление пополам» ...

В итоге...

Задаётся вопрос: «число меньше 𝑁 ?». Любой из ответов «да» и «нет» сократит область поиска вдвое. Далее по той же схеме диапазон снова делится пополам. В конечном счёте загаданное число будет найдено.

Допустим, загаданное число 27. Вариант диалога:

— Больше 50? Нет.

— Больше 25? Да.

— Больше 38? Нет.

— Меньше 32? Да.

— Меньше 29? Да.

— Меньше 27? Нет.

— Это число 28? Нет. это число 27.

\Rightarrow

И какая тут зависимость?

А вот такая...

\lceil \log_2 N \rceil = \lceil \log_2 100 \rceil = 7.

Содержательный подход к измерению информации

Информация — это снятая неопределенность. Величина неопределенности некоторого события — это количество возможных исходов этого события.

Чем более вероятно наступление какого-либо события, тем меньшее количество информации несет для нас сообщение о наступлении этого события.

Один бит — это такое количество информации, которое уменьшает неопределенность в два раза.

Формула Хартли

I = \log_2 N

Если все исходы какого-то события равновероятны, то количество информации о наступление того или иного исхода определяется формулой Хартли, которую впервые записал в 1928 году американский инженер Ральф Хартли:

— количество информации,

— количество возможных событий.

Что такое равновероятные события?

Равновероятные события

1. при бросании монеты:

«выпала решка», «выпал орел»;

2. при бросании игральной кости:

появление одной из цифр кости (1, 2, 3, ..., 6);

3. при вытягивании карты из колоды: появление карты какой-либо масти и ранга (с одной оговоркой — какой?);

Являются ли равновероятными сообщения

«первой выйдет из дверей здания женщина»

«первым выйдет из дверей здания мужчина»?

Формула Шеннона

I = -\sum \limits_{i}^N p_{i}\log_{2} p_{i}

Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе:

— количество информации,

— вероятность -го события.

— количество возможных событий.

p_i

Задачи

1. В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?

2. Сообщение о том, что ваш друг живет на 6 этаже несет 4 бита информации. Сколько этажей в доме.

3. Найти количество информации в однозначном сообщении.

4. Какое количество информации потребуется для кодирования одного шахматного поля?

Задачи (2)

5. Сколько информации содержит сообщение о выпадении грани с числом 3 на шестигранном игральном кубике?

6. Сколько вопросов следует задать и как их нужно сформулировать, чтобы узнать с какого из 16 путей отправляется ваш поезд?

7. За четверть ученик получил 100 оценок. Сообщение о том, что он получил четверку, несет 2 бита информации. Сколько четверок ученик получил за четверть?

Задачи (3)

8. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

9. В озере живут караси и окуни. Подсчитано, что карасей — 1500, а окуней — 500. Сколько информации содержится в сообщениях о том, что рыбак поймал карася, окуня, поймал рыбу?

10. В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара.

Алфавитный подход к измерению информации

Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита. Такой подход не связан с содержанием текста.

Алфавит — упорядоченный набор символов, используемый для кодирования сообщений на некотором языке.

Мощность алфавита — количество символов алфавита.

Примеры алфавитов:

B = \{A, B, C, ... Z\}

|B| = 26

A = \{0, 1\}

|A| = 2

C = \{\text{А}, \text{Б}, \text{В}, ... \text{Я}\}

|С| = 33

Алфавитный подход к измерению ифнормации

Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле Хартли:

I = \log_2 N

— количество информации, которое несёт один символ

— мощность алфавита.

Количество информации в сообщении

V = K \cdot I

— количество информации, которое несёт один символ

— количество символов в соощении.

Задачи

1. В велокроссе участвуют 28 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Какой объём памяти будет использован устройством, когда все спортсмены прошли промежуточный финиш?

2. В велокроссе участвуют 915 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая номер участника с использованием минимально возможного количества бит, одинакового для всех спортсменов. Какой объём памяти будет использован устройством, когда промежуточный финиш прошли 560 велосипедистов?

Задачи (2)

3. В некоторой стране автомобильный номер состоит из 8 символов. Первый символ — одна из 26 латинских букв, остальные семь — десятичные цифры. Пример номера — A1234567. Каждый символ кодируется минимально возможным количеством бит, а каждый номер — одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 30 автомобильных номеров.

4. Для регистрации на сайте некоторой страны пользователю необходимо придумать пароль длиной ровно 11 символов. В пароле можно использовать десятичные цифры и 12 различных символов местного алфавита, причем все буквы используются в двух начертаниях — строчные и прописные. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый пароль — одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 60 паролей.