Вавилонская библиотека

Вавилонская библиотека — это библиотека, в которой есть всё. Всё, что когда-либо было, есть или будет, все события, изобретения, имена, все литературные произведения, которых даже пока не существует, вся история вселенной — всё это есть в этой библиотеке.

Как это возможно?

Вавилонская библиотека

Библиотека состоит из шестигранных комнат, в каждой из которых имеется по двадцать полок, на каждой из которых находятся тридцать две книги одного формата, во всех книгах по четыреста десять страниц, на странице сорок строк, в строке около восьмидесяти букв чёрного цвета, которые допускают двадцать пять орфографических символов: 22 буквы, точку, запятую и пробел.

 

Большинство книг абсолютно бессмысленны, так как они являют собой комбинаторный перебор всех возможных вариантов двадцати пяти знаков. Однако эти варианты никогда не повторяются, главный закон библиотеки: в библиотеке не бывает двух одинаковых книг. Поэтому количество книг конечно и библиотека имеет границы.

Комбинаторика

10 класс

 

vkrysanov320@gmail.com

 

Комбинаторика

Комбинаторика — раздел математики, в котором изучаются вопросы о том, сколько различных конфигураций (комбинаций), подчиненных тем или иным условиям, можно составить из заданных объектов.

Правило суммы

Если элемент     можно выбрать     различными способами и независимо от него элемент     можно выбрать      различными способами, то выбрать  «     или     » можно                способами.

A
B
n
m
A
B
n + m
\xRightarrow[\text{синий \textbf{или} красный}]{\text{выбираем 1 шар}}
\underbrace{\hspace{1cm}}_{n=3}
\underbrace{\hspace{1cm}}_{m=5}
3 + 5 = 8\text{ способов}.

*любой цвет из данных

связка «или» указывает на использование правила суммы

Дежурные

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить дежурного?

Дежурные. Решение

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

16 + 10 = 26

                              способов (по правилу сложения, т.к. дежурным можно назначить либо мальчика, либо девочку).


Правило произведения

Если элемент     можно выбрать     способами, и при любом выборе элемент     можно выбрать      способами, то пару             можно выбрать

            способами.

a
b
n
m
(a, b)
n\cdot m
\xRightarrow[\text{синий \textbf{и} красный}]{\text{выбираем пару шаров}}
\underbrace{\hspace{1cm}}_{n=3}
\underbrace{\hspace{1cm}}_{m=5}
3 \cdot 5 = 15\text{ способов}.

*(красный, синий)

связка «и» указывает на использование правила произведения

a

И опять дежурные...

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Дежурные (2). Решение

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

16 + 10 = 26

1) Назначаем первого дежурного:                               способов (по правилу сложения, т.к. первым дежурным можно назначить либо мальчика, либо девочку).

 

2) Теперь мы можем выбрать второго дежурного из оставшихся       учеников, т.е.  способами.

 

3) Таким образом, дежурные могут быть выбраны                                способами (по правилу произведения).

25
25
26 \cdot 25 = 650

Задача 1

Имеются три города: A, B и C. Из A в B ведут три дороги, из B в C — пять дорог. Сколько различных путей ведут из A в C? Прямого пути между A и C нет.

 

Задача 1. Решение

Обозначим дороги буквами и цифрами. Именно, дороги из A в B назовём a, b, c; дороги из B в C назовём 1, 2, 3, 4, 5.

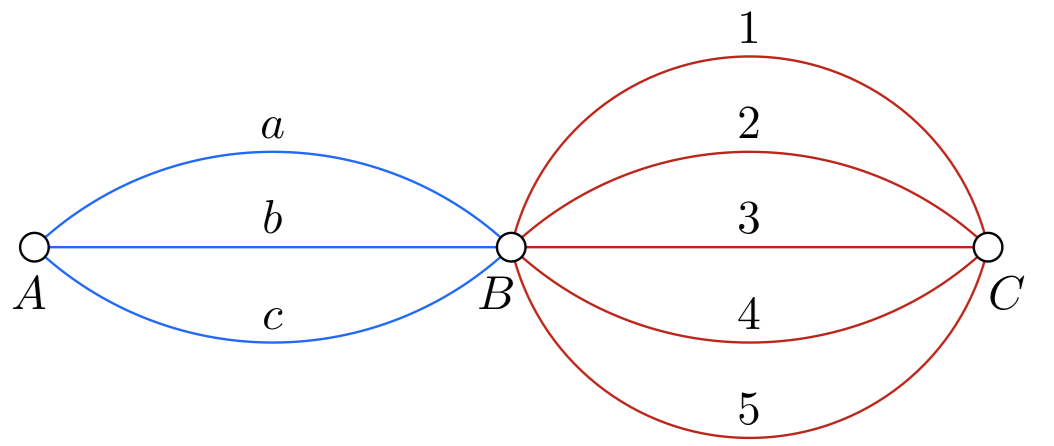
Или же, по правилу произведения, число маршрутов равно произведению числа дорог из A в B на число дорог из B в C, т.е.

3 \cdot 5 = 15.

Таким образом, любой маршрут из A в C получает уникальное имя в виде пары из буквы и цифры:

a1 a2 a3 a4 a5
b1 b2 b3 b4 b5
c1 c2 c3 c4 c5
\Sigma = 15.

*полный перебор значений

Задача 2

Сколько существует пятизначных чисел, у которых все цифры чётные?

Задача 2. Решение

Сколько существует пятизначных чисел, у которых все цифры чётные?

a_2
a_4
a_3
a_5
a_1
a_1 \in \underbrace{\{ 2,4,6,8\}}_{n=4}
a_2, a_3, a_4, a_5 \in \underbrace{\{ 0, 2,4,6,8\}}_{n=5}
\Sigma = 4 \cdot 5 \cdot 5 \cdot 5 \cdot 5 = 2500.

Задача 3

В магазине есть 7 видов пиджаков, 5 видов брюк и 4 вида галстуков. Сколькими способами можно купить комплект из пиджака, брюк и галстука?

Задача 3. Решение

В магазине есть 7 видов пиджаков, 5 видов брюк и 4 вида галстуков. Сколькими способами можно купить комплект из пиджака, брюк и галстука?

...

\times 7
\Rightarrow 7 \cdot 5 \cdot 4 = 140 \text{ способов.}

Задача 4

В магазине «Все для чая» продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?

 

Задача 4. Решение

В магазине «Все для чая» продается 5 чашек, 3 блюдца и 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?

5\cdot 3 = 15
3\cdot 4 = 12
4\cdot 5 = 20
\left. \begin{array}{ccc} \\ \\ \\ \\ \\ \\ \end{array} \right\}
\Sigma = 47

Факториал

n! = \prod \limits_{i=1}^{n} i = 1 \cdot 2 \cdot 3 \cdot ... \cdot n.

Факториал (от лат. factorialis — действующий, производящий, умножающий) — функция, определённая на множестве неотрицательных целых чисел. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:

Свойства факториала

n!= \begin{cases} 1, \text{ если } n = 0;\\ n \cdot (n-1)!, \text{ если } n > 0. \end{cases}
0! = 1.

3) Факториал нуля равен единице:

1) Рекуррентная формула:

2) Из 1) вытекает:

n! = \frac{(n+1)!}{n+1}.
0! = \frac{(0+1)!}{0+1} = \frac{1!}{1} = \frac{1}{1} = 1

Неполный факториал

n^{\underline{k}} = n\cdot (n-1)\cdot \ldots\cdot (n-k+1) = \frac{n!}{(n-k)!} = \prod_{i=n-k+1}^n i.
n^{\overline{k}} = n\cdot (n+1)\cdot \ldots\cdot (n+k-1) = \frac{(n+k-1)!}{(n-1)!}=\prod_{i=n}^{(n+k)-1} i.

Убывающий факториал:

Возрастающий факториал:

Другие виды факториальных функций

\mathrm{sf}(n) = \prod \limits_{i=1}^n i!

Суперфакториал:

Праймориал — определяется как произведение n первых простых чисел. К примеру, праймориал от 5:

p_{5}\#=2\times 3\times 5\times 7\times 11=2310.

Обозначение праймориала

Обозначение суперфакториала

!n=n!\left(1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+...+(-1)^{n}{\frac {1}{n!}}\right)=n!\sum \limits_{{k=0}}^{n}{\frac {(-1)^{k}}{k!}}

Субфакториал:

Что такое упорядоченный набор? А что такое неупорядоченный набор?

\begin{cases} x + y = 3;\\ x - y = 1. \end{cases}

Упорядоченный набор

Решим систему уравнений:

x = 2; y = 1.

Явно

Также ответ можно записать в виде пары

(2; 1).

Такую пару называют упорядоченной, поскольку порядок следования чисел важен; записывая ответ, мы не можем поменять числа местами.

x
y

Запись

(1; 2)

будет обозначать

x = 1; y = 2

что не будет решением

a_1, a_2, ..., a_k

Цепочка (или упорядоченный набор), составленная по порядку из элементов                       , записывается                  или                         ; число       называется длиной цепочки. При изменении порядка следования элементов мы, вообще говоря, получим другую цепочку (той же длины).

a_1a_2 ... a_k
\langle a_1, a_2, ... , a_k \rangle
k

системы.

x^2 - 3x + 2 = 0.

Неупорядоченный набор

Решим уравнение:

Мы записываем пару этих корней в виде           . Такую пару называют неупорядоченной, поскольку порядок следования чисел в данной записи не играет роли;

Пары            и            — это одна и та же неупорядоченная пара.

Его корнями служат числа 1 и 2.

\{1, 2\}
\{1, 2\}
\{2, 1\}

Еще примеры:

Множество корней уравнения:                                        —    

Множество букв русского алфавита:

Множество букв слова «математика» —

x(x-1)(x-2) = 0
\{0, 1, 2\}
\{\text{а, б, в, . . . , ю, я}\}
\{\text{м, а, т, е, и, к}\}

Размещения

Пусть имеется множество, содержащее     элементов. Произвольный
упорядоченный набор, составленный из    различных элементов данного множества, называется размещением из     элементов по элементов (или просто размещением из     по    ).

n
k
n
k
n
k

*Множество из которого составляем наборы

Упорядоченные наборы:

A_n^k = \frac{n!}{(n-k)!}
A_3^2 = \frac{3!}{(3-2)!} = 3! = 6

Задача 1

В футбольной команде 11 человек.
Сколькими способами можно выбрать: капитана, первого ассистента и второго ассистента?

Задача 1. Решение

В футбольной команде 11 человек. Сколькими способами можно выбрать: капитана, первого ассистента и второго ассистента?

A_{11}^3 = \frac{11!}{(11-3)!} = \frac{11!}{8!} = \frac{8! \cdot 9 \cdot 10 \cdot 11}{8!} = 9 \cdot 10 \cdot 11 = 990.

Задача 2

Сколькими способами могут быть заняты первое, второе и третье места (по одному человеку на место) на соревнованиях, в которых участвуют:

а) 5 человек;

б) 6 человек?

 

Задача 2. Решение

A_{5}^3 = \frac{5!}{(5-3)!} = \frac{5!}{2!} = \frac{2! \cdot 3 \cdot 4 \cdot 5}{2!} = 3 \cdot 4 \cdot 5 = 60.

Сколькими способами могут быть заняты первое, второе и третье места (по одному человеку на место) на соревнованиях, в которых участвуют:

а) 5 человек;

 

​

б) 6 человек?

 

A_{6}^3 = \frac{6!}{(6-3)!} = \frac{6!}{3!} = \frac{3! \cdot 4 \cdot 5 \cdot 6}{3!} = 4 \cdot 5 \cdot 6 = 120.

Задача 3

Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?

Задача 3. Решение

Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?

 

A_{10}^6 = \frac{10!}{(10-6)!} = \frac{10!}{4!} = \frac{4! \cdot 5 \cdot 6 \cdot 7\cdot 8 \cdot 9 \cdot 10}{4!} = 5 \cdot 6 \cdot 7\cdot 8 \cdot 9 \cdot 10 = 151200.

Перестановки

Пусть имеется множество, содержащее     элементов. Произвольный
упорядоченный набор длины    составленный из всех элементов данного множества, называется перестановкой этого множества (или перестановкой     элементов). Иными словами, перестановка  элементов — это размещение из     по    .

 

n
n
n
n
n
n
\underbrace{\hspace{4cm}}_{6\text{ различных перестановок}}
P_n = n!
P_3 = 3! = 6

Задача 1

Сколькими способами 28 учеников могут выстроиться в очередь в столовую?

Задача 1. Решение

Сколькими способами 28 учеников могут выстроиться в очередь в столовую?

P_{28}=28!.

Задача 2

Сколько различных слов  можно получить переставляя буквы слова «ВЕКТОР»?

Задача 2. Решение

Сколько различных слов  можно получить переставляя буквы слова «ВЕКТОР»?

Так как все буквы слова различны, то всего можно получить       слов.

То есть                            слов.

P_6
P_6 = 6! = 720

Задача 3

Сколько различных слов  можно получить переставляя буквы слова «ПАРАБОЛА»?

Задача 3. Решение

Сколько различных слов  можно получить переставляя буквы слова «ПАРАБОЛА»?

Считая три буквы А этого слова различными                       , получим   разных слов. Однако, слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы                       можно переставлять      способами, все      слов разбиваются на группы по

одинаковых. Поэтому разных слов всего:

P_8
\frac{P_8}{P_3} = \frac{8!}{3!}.
(A_1, A_2, A_3)
A_1, A_2, A_3
P_3
P_8
P_3

Задача 4

В футбольной команде 11 человек. Сколькими способами можно выбрать из них двух игроков для прохождения допинг-контроля?

Задача 4. Решение

В футбольной команде 11 человек. Сколькими способами можно выбрать из них двух игроков для прохождения допинг-контроля?

A_{11}^2 = ...

Почему данная комбинаторная схема не подходит?

Сочетания

Пусть имеется множество, содержащее      элементов. Произвольный неупорядоченный набор, состоящий из      различных элементов данного множества, называется сочетанием из     элементов по элементов (или просто сочетанием из     по    ).

n
k
n
k
n
k

или

или

или

\left. \begin{array}{ccc} \\ \\ \\ \\ \\ \\ \end{array} \right\}
3\text{ сочетания}
C_n^k = \frac{A_n^k}{k!} = \frac{n!}{k!(n-k)!}
C_3^2 = \frac{3!}{2!(3-2)!} = \frac{3!}{2!} = \frac{6}{2} = 3

Вернёмся к задаче со спортсменами

В футбольной команде 11 человек. Сколькими способами можно выбрать из них двух игроков для прохождения допинг-контроля?

В данном случае пара человек, отправленный на допинг-тест,
является неупорядоченной: отправить Петю и Васю на тест — это ровно то же самое, что отправить Васю и Петю на тест. Соответственно, в данной задаче нас интересует именно число неупорядоченных пар
футболистов, выбираемых из 11 человек.

C_{11}^2 = \frac{11!}{2!(11-2)!} = \frac{11!}{2!9!} = \frac{9! \cdot 10 \cdot 11}{2!9!} = \frac{10 \cdot 11}{2!} = \frac{110}{2} = 55.

Задача 1

Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?

Задача 1. Решение

Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?

C_{10}^3 = \frac{10!}{3!(10-3)!} = \frac{10!}{3!7!} = \frac{7! \cdot 8 \cdot 9 \cdot 10}{3!7!} = \frac{8 \cdot 9 \cdot 10}{3!} = \frac{720}{6} = 120.

Задачи

1. Монету подбрасывают 8 раз. При этом получается некоторая последовательность «орлов» и «решек» (длины 8). Сколько всего существует таких последовательностей, в которых «орёл» выпал ровно три раза?

2. Из 30 участников собрания надо выбрать предсе­дателя и секретаря. Сколькими способами это можно сделать?

3. Сколькими способами можно выбрать 4 краски из имеющихся 7 различных?

4. Рота состоит из трёх офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?

5. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?


Размещения с повторениями

В отличие от обычных размещений, в размещениях с повторениями
каждый объект может участвовать несколько раз. Это больше похоже на перебор различных комбинаций кодового замка.

\overline{A}_n^k

Количество размещений с повторениями обозначается как       , где

— размер множества из которого выбираются элементы, а     — по скольку выбирается.

 

Количество размещений находится по формуле:
 

k
n
\overline{A}_n^k = \underbrace{n \cdot n \cdot ... \cdot n}_{k\text{-раз}} = n^k

Кодовый замок

Сколько различных комбинаций имеет кодовый замок у которого 6 барабанов с 10 цифрами на каждом?

\underbrace{\hspace{4cm}}_{6\text{ барабанов}}
a_1
a_2
a_3
a_4
a_5
a_6
a_i \in \{0,...,9\}
\Sigma = \overline{A}_{10}^6 = 10^6=1000000.

Задача 1

Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если:

а)первая из них не равна нулю;

б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?

Задача 1. Решение

Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если:

а) первая из них не равна нулю;

б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?

а)                                                                             б)

\Sigma = \overline{A}_{9}^1 \cdot \overline{A}_{10}^4 = 9 \cdot 10^4.
\Sigma = \overline{A}_{26}^1 \cdot \overline{A}_{9}^4 = 26 \cdot 9^4.

цифра, отличая от нуля

одна любая буква

четыре цифры, отличные от нуля

четыре любые цифры

Перестановки с повторениями

Последовательность длины    , составленная из     разных символов, первый из которых повторяется       раз, второй —      раз, третий —   раз, ...,    -й  —       раз (где                                         ) называется перестановкой с повторениями из    элементов.

n_1
k
n
n_2
n_3
k
n_k
n_1+ n_2+... + n_k = n
n

Число перестановок с повторениями длины     из     разных элементов, взятых соответственно по                        раз каждый обозначается:

n
k
n_1,n_2,..., n_k
\overline{P}(n_1,n_2,..., n_k) = \frac{n!}{n_1! \cdot n_2! \cdot ... \cdot n_k!}
abac, baac, aabc, aacb, abca, baca, acba, acab, bcaa, cbaa, caba, caab.

Для набора из четырех букв          все перестановки с повторениями будут такими:

aabc
\underbrace{\hspace{10cm}}_{12\text{ различных перестановок}}
\overline{P}(2,1,1) = \frac{4!}{2!} = 12

Задача 1

Сколько различных слов  можно получить переставляя буквы слова «ПАРАБОЛА»?

Задача 1. Решение

Сколько различных слов  можно получить переставляя буквы слова «ПАРАБОЛА»?

П А Р Б О Л
1 3 1 1 1 1
\overline{P}(1,3,1,1,1,1) = \frac{8!}{3!}.
\underbrace{\hspace5cm}_{8}
\Leftarrow

Сочетания с повторениями

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

\overline{C}^k_n = \overline{P}(k, n-1) = C^k_{k+n-1}

Для множества                        все сочетания с повторениями из множества     по 2 будут такими:

A = \{1,2,3\}
A
1,1; 1,2; 1,3; 2,2; 2,3; 3,3.
\underbrace{\hspace{4cm}}_{6\text{ сочетаний}}
\overline{C}^2_3 = C^2_{2+3-1} = C^2_{4} = \frac{4!}{2!(4-2)!} = \frac{4!}{2!2!}= \frac{24}{4} = 6

Число сочетаний с повторений из    -элементного множества по элементов обозначается:

k
n

Задача 1

На почте пять видов открыток к Новому году. Сколькими способами из них можно выбрать семь открыток?

Задача 1. Решение

На почте пять видов открыток к Новому году. Сколькими способами из них можно выбрать семь открыток?

\overline{C}^7_5 = C^7_{7+5-1} = C^7_{11} = \frac{11!}{7!(11-7)!} = \frac{11!}{7!4!} = 330.

Задача 2

В магазине продаются булочки трёх видов: с маком, изюмом и повидлом. Мама послала Колю купить 6 булочек. Сколько возможных вариантов выбора у него есть?

Задача 2. Решение

В магазине продаются булочки трёх видов: с маком, изюмом и повидлом. Мама послала Колю купить 6 булочек. Сколько возможных вариантов выбора у него есть?

\overline{C}^6_3 = C^6_{6+3-1} = C^6_{8} = \frac{8!}{6!(8-6)!} = \frac{8!}{6!2!} = 28.

Распределение по группам

Группа из 25 студентов делится на три подгруппы, в первую входят 5 человек, во вторую — 8, а в третью — 12. Сколькими способами это можно сделать?

 

Распределение по группам. Решение

Группа из 25 студентов делится на три подгруппы, в первую входят 5 человек, во вторую — 8, а в третью — 12. Сколькими способами это можно сделать?

C^5_{25}
C^8_{20}
C^{12}_{12}

I группа

II группа

III группа

\Leftarrow
\Sigma = C^5_{25} \cdot C^8_{20} \cdot C^{12}_{12}

Применяя правило произведения

Олимпиада по программированию

В олимпиаде по программированию может участвовать команда из трех студентов группы.
Сколько возможностей составить команду, если в группе 20 студентов?

Олимпиада по программированию. Решение

В олимпиаде по программированию может участвовать команда из трех студентов группы. Сколько возможностей составить команду, если в группе 20 студентов?

\Sigma = C^3_{20} = \frac{20!}{3!(20-3)!} = \frac{20!}{3!17!} = 1140.

Составляем слова

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

 

Составляем слова. Решение

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

 

С * * * Г
\overline{A}_2^1
\overline{A}_2^1
\overline{A}_4^3
\underbrace{\hspace{2cm}}
\Sigma = \overline{A}_2^1 \cdot \overline{A}_4^3 \cdot \overline{A}_2^1 = 2^1 \cdot 4^3 \cdot 2^1 = 256.
\Leftarrow

Применяя правило произведения

Задача с карточками

Сколько пятибуквенных слов можно образовать из следующих карточек

\boxed{С}
\boxed{А}
\boxed{П}
\boxed{Ф}
\boxed{И}
\boxed{Р}

Сколько среди них таких, которые не содержат карточки       ?

Сколько таких, которые начинаются с карточки         и оканчиваются карточкой       ?

 

\boxed{Р}
\boxed{С}
\boxed{Р}

Задача с карточками. Решение

Сколько пятибуквенных слов можно образовать из следующих карточек

\boxed{С}
\boxed{А}
\boxed{П}
\boxed{Ф}
\boxed{И}
\boxed{Р}

Сколько среди них таких, которые не содержат карточки       ?

\boxed{Р}
\boxed{С}
\boxed{Р}
\Sigma = A_6^5 = \frac{6!}{(6-5)!} = 6!.

Сколько таких, которые начинаются с карточки         и оканчиваются карточкой       ?

\Sigma = A_5^5 = 5! = 120.
\Sigma = 1 \cdot A_4^3 \cdot 1 = \frac{4!}{(4-3)!} = 4! = 24.

Левий

Левий составляет 5-буквенные коды из букв Л, Е, В, И, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания ЕИ. Сколько различных кодов может составить Левий?

 

Левий. Решение

Левий составляет 5-буквенные коды из букв Л, Е, В, И, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания ЕИ. Сколько различных кодов может составить Левий?

 

Е И * * *
* Е И * *
* * Е И *
* * * Е И
\Sigma_1 = A_4^4 = 4! = 24
Й * * * *

Случаи с Й в начале:

Случаи с ЕИ:

\Sigma_2 = A_3^3 = 3! = 6
\left. \begin{array}{ccc} \\ \\ \end{array} \right\}

Помним, что все случаи с Й в начале мы исключили!

\Sigma_3 = 3(A_2^2 \cdot A_2^2 \cdot 1) = 3 \cdot 4 = 12
\Sigma = \Sigma' - \Sigma_1 - \Sigma_2 - \Sigma_3 = 120 - 24 - 6 - 12 = 78.

Все переборы:

\Sigma' = P_5 = 5! = 120

Ольга

Ольга составляет 5-буквенные коды из букв О, Л, Ь, Г, А. Каждую букву нужно использовать ровно 1 раз, при этом Ь нельзя ставить первым и нельзя ставить после гласной. Сколько различных кодов может составить Ольга?

 

Ольга. Решение

Ольга составляет 5-буквенные коды из букв О, Л, Ь, Г, А. Каждую букву нужно использовать ровно 1 раз, при этом Ь нельзя ставить первым и нельзя ставить после гласной. Сколько различных кодов может составить Ольга?

Ь * * * *
Г Ь * * *
* Г Ь * *
* * Г Ь *
* * * Г Ь

Случаи с Ь:

Все переборы:

\Sigma' = P_5 = 5! = 120
\Sigma_1 = A_4^4 = 4! = 24
\Sigma_2 = 4(A_2^1 \cdot 1 \cdot A_3^3) = 4 \cdot 2 \cdot 6 = 48
\left. \begin{array}{ccc} \\ \\ \\ \end{array} \right\}

Таким образом:

\Sigma = \Sigma' - \Sigma_1 - \Sigma_2 = 120 - 24 - 48 = 48.

Немного некомбинаторная задача

Все 4-бук­вен­ные слова, со­став­лен­ные из букв Н, Р, Т, У, за­пи­са­ны в алфа­вит­ном по­ряд­ке. Вот на­ча­ло спис­ка:

1. НННН
2. НННР
3. НННТ
4. НННУ
5. ННРН

Какое слово, ко­то­рое стоит на 215-м месте от начала списка?

Решение

В данном случае можно представить список данных слов в четверичной системе счисления: Н — 0, Р — 1, Т — 2, У — 3. Таким образом начало списка будет следующим:

1. НННН — 0000
2. НННР — 0001
3. НННТ — 0002
4. НННУ — 0003
5. ННРН — 0004

Значит, чтобы понять, какое слово стоит на 215-м месте от начала списка, необходимо                  перевести в четверичную

систему счисления (минус 1, так как список начинается с 0000) и произвести замену на буквы:

214_{10} = 3112_{4} \Rightarrow \text{ УРРТ.}
215 - 1

Билеты в театр

Сколькими способами можно распределить три билета в театр между 20 студентами, если

 

1) распределяются билеты в разные театры, а каждый студент может получить не более одного билета;

 

2) распределяются билеты в разные театры и на разные дни, а каждый студент может получить любое (не превышающее трех) число билетов;

 

3) распределяются равноценные билеты на вечер, и каждый студент может получить не более одного билета?

Билеты в театр. Решение (1)

Сколькими способами можно распределить три билета в театр между 20 студентами, если распределяются билеты в разные театры, а каждый студент может получить не более одного билета.

  • в данном случае выборка без повторений, т.к. каждый студент может получить не более одного билета.
  • порядок важен, в виду того, что билеты разные.
  • следовательно, число возможных способов распределений билетов равно числу размещений без повторений:
\Sigma = A_{20}^3 = \frac{20!}{(20-3)!} = \frac{20!}{17!} = 18 \cdot 19 \cdot 20 = 6840.

Билеты в театр. Решение (2)

Сколькими способами можно распределить три билета в театр между 20 студентами, если распределяются билеты в разные театры и на разные дни, а каждый студент может получить любое (не превышающее трех) число билетов.

  • каждый студент может получить более одного билета, значит, имеем дело с выборкой с повторениями;
  • порядок важен, в виду того, что билеты разные;
  • следовательно, число возможных способов распределений билетов равно числу размещений с повторениями:
\Sigma = \overline{A}_{20}^{3} = 20^{3}.

Билеты в театр. Решение (3)

Сколькими способами можно распределить три билета в театр между 20 студентами, если распределяются равноценные билеты на вечер, и каждый студент может получить не более одного билета.

  • каждый студент может получить не более одного билета, значит, имеем дело с выборкой без повторений;

  • порядок не важен, в виду того, что билеты равноценные;

  • следовательно, число возможных способов распределений билетов равно числу сочетаний без повторений:

\Sigma = C^3_{20} = \frac{20!}{3!(20-3)!} = \frac{20!}{3!17!} = 1140.

Беспорядки

Беспорядок (англ. Derangement) — это перестановка чисел от     до    , в которой ни один элемент не стоит на своём месте. Количество беспорядков порядка     равно субфакториалу числа    :

1
n
D(n) = !n = n!-{\frac {n!}{1!}} + {\frac {n!}{2!}} - {\frac {n!}{3!}}+ ... + (-1)^{n}{\frac {n!}{n!}}= \sum \limits_{k=0}^{n}(-1)^{k}{\frac {n!}{k!}}
n
n

Профессор дал четырём студентам (                 ) контрольную, а затем предложил им проверить её друг у друга. Ни один студент не должен проверять свою контрольную. Сколько у профессора вариантов распределения контрольных, в которых ни одному студенту не достанется своя работа?

D(4) = !4 = 4!-{\frac {4!}{1!}} + {\frac {4!}{2!}} - {\frac {4!}{3!}}+ {\frac {4!}{4!}} = 24 - 24 +12 - 4 + 1 = 9.
BADC, BCDA, BDAC, CADB, CDAB, CDBA, DABC, DCAB, DCBA.
A, B, C, D
\underbrace{\hspace{10cm}}_9
Made with Slides.com