VGG type Network​

  1. ConvBlock (32, 360, 360)
  2. ConvBlock (64, 180, 180)
  3. ConvBlock (128, 90, 90)
  4. ConvBlock (256, 45, 45)
  5. ConvBlock (512, 22, 22)
  6. Global Average Pooling
  7. Dense(2)

 

ConvBlock

  1. Conv3x3 + BN + ELU
  2. Conv3x3 + BN + ELU
  3. MaxPool (2, 2)
  • Batch: 32
  • Optimizer: Adam
  • LR: 1e-4
  • 5 fold
  • Loss: L1
  • Augmentation: flips

Training

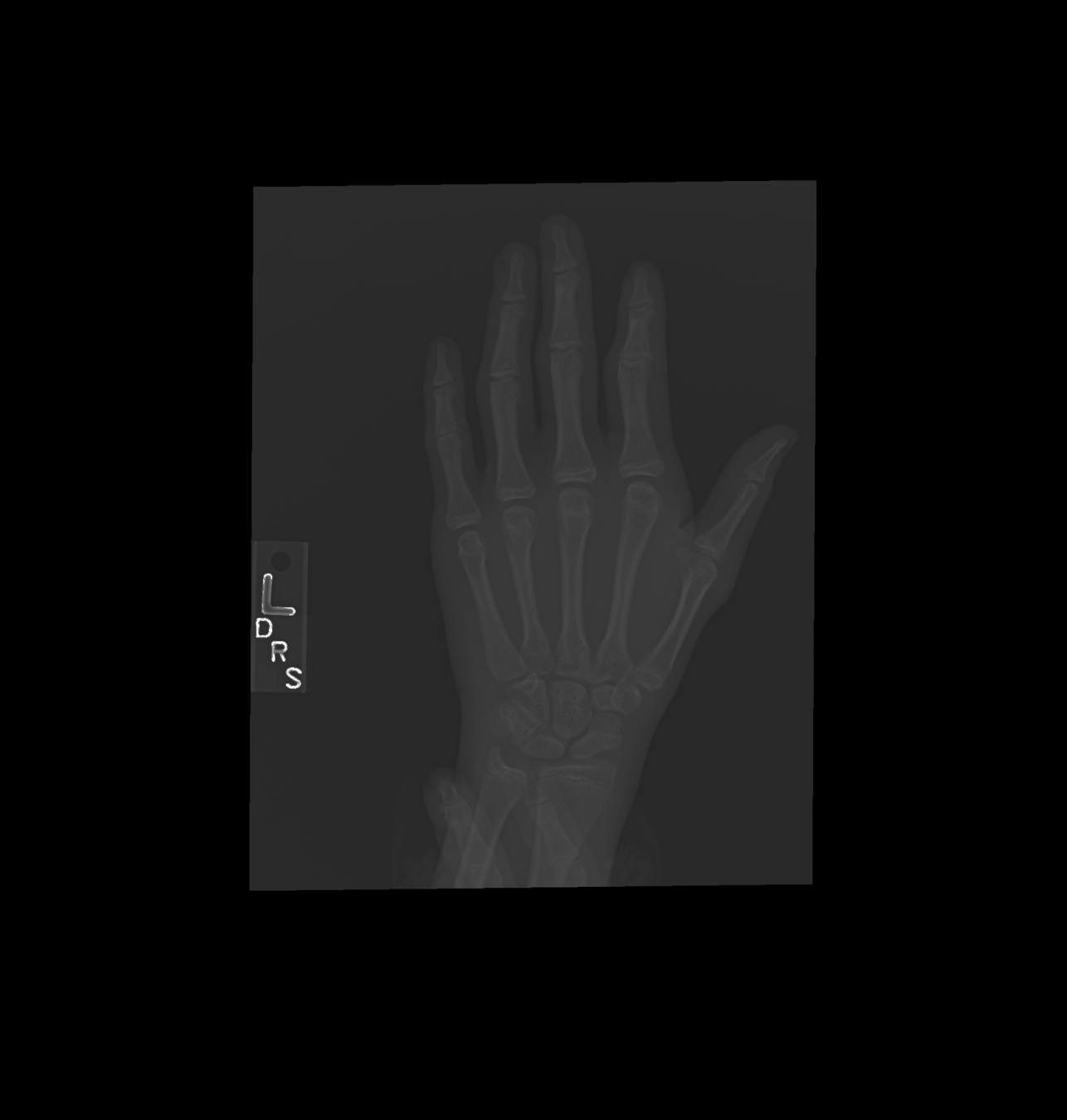
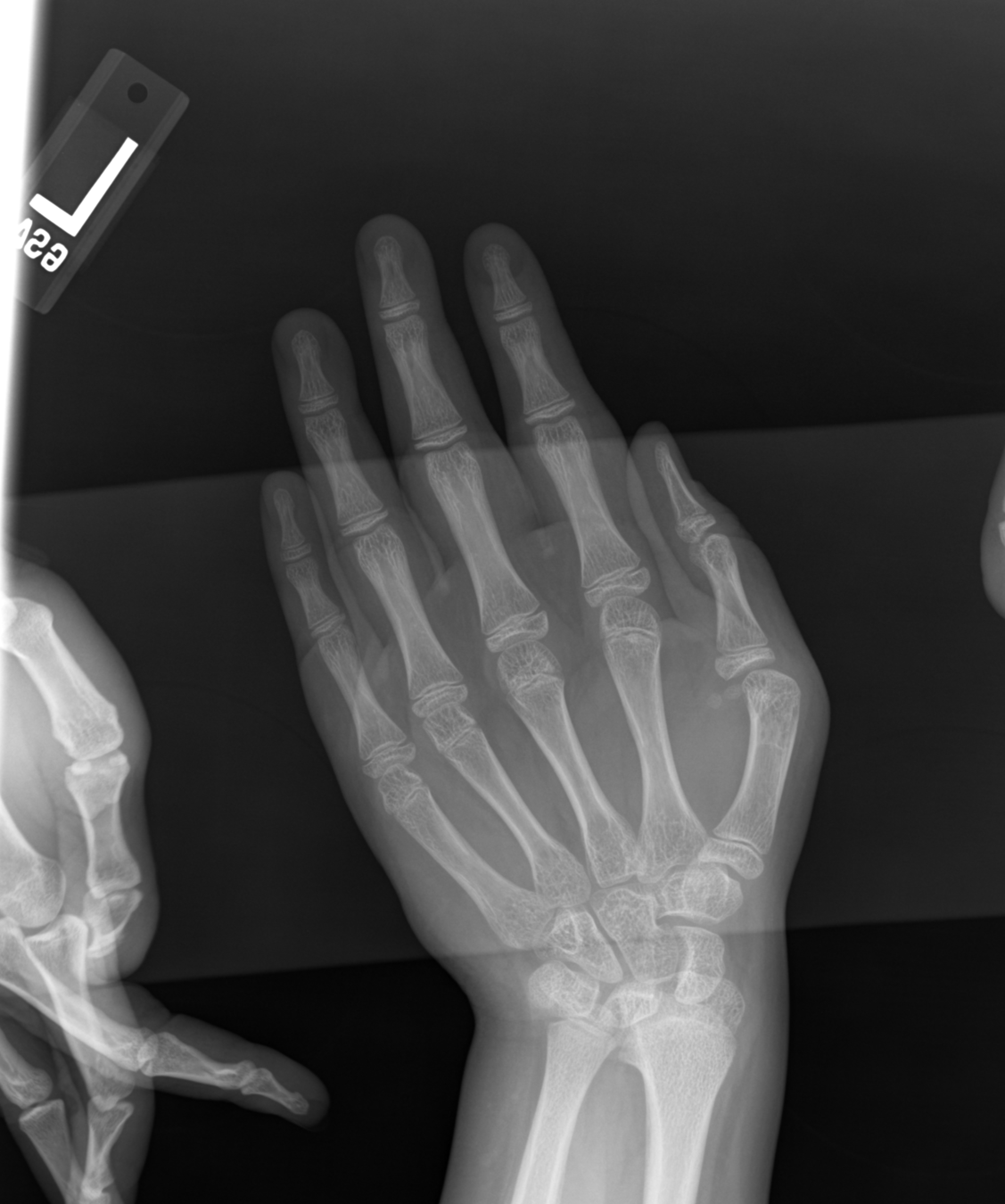
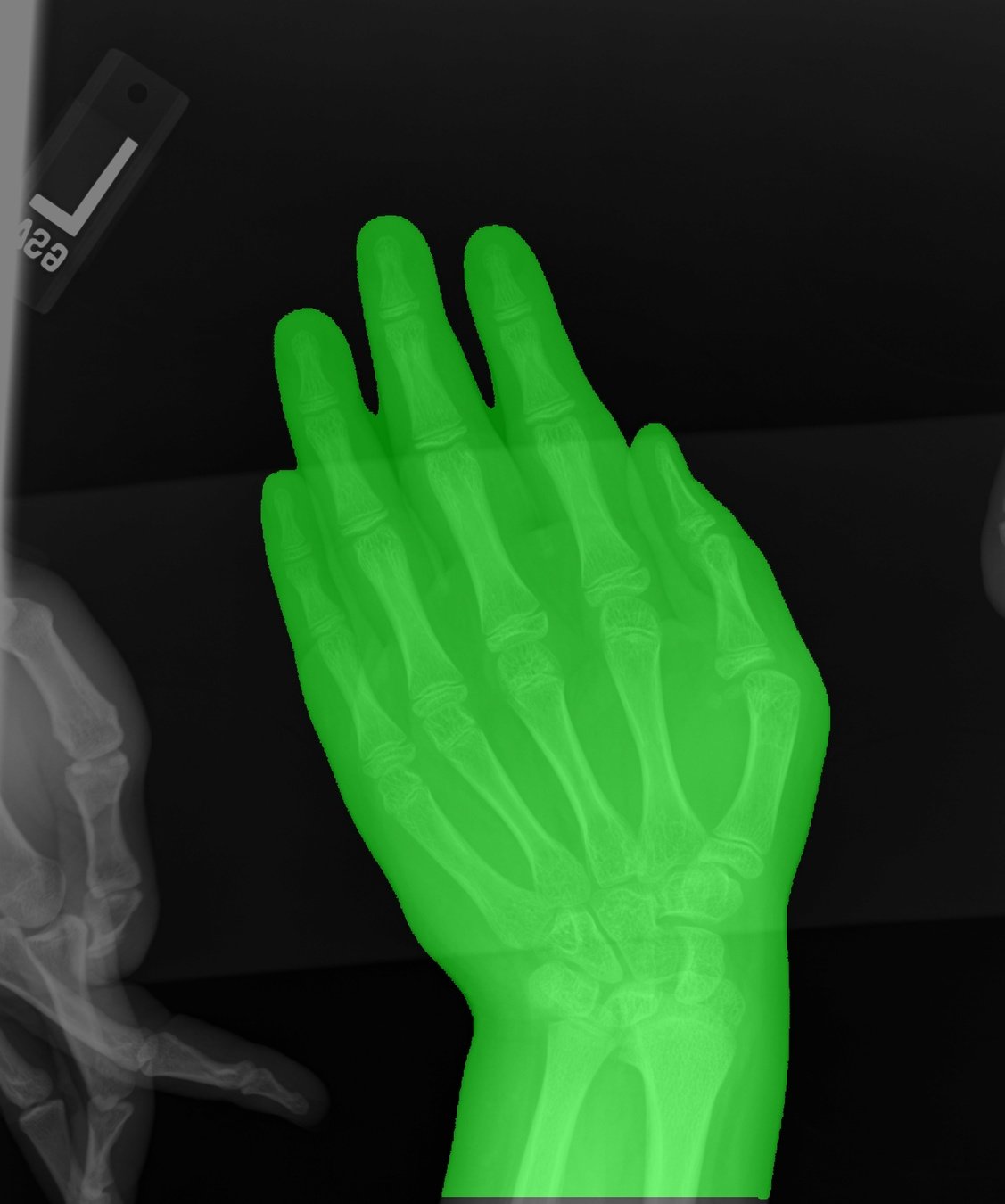
A

B

 

C

D

E

F

BCE = - \sum_i \left( y_i \ln (p_i) + (1 - y_i) \ln(1 - p_i)\right)
BCE=−∑i(yiln(pi)+(1−yi)ln(1−pi))BCE = - \sum_i \left( y_i \ln (p_i) + (1 - y_i) \ln(1 - p_i)\right)
DICE = 2 \frac {\sum_i y_i p_i} {\sum_u y_i + \sum p_i}
DICE=2∑iyipi∑uyi+∑piDICE = 2 \frac {\sum_i y_i p_i} {\sum_u y_i + \sum p_i}
LOSS = BCE - \ln \left( DICE \right)
LOSS=BCE−ln(DICE)LOSS = BCE - \ln \left( DICE \right)
BCE = - \sum_i \left( y_i \ln (\hat{y_i}) + (1 - y_i) \ln(1 - \hat{y_i})\right)
BCE=−∑i(yiln(yi^)+(1−yi)ln(1−yi^))BCE = - \sum_i \left( y_i \ln (\hat{y_i}) + (1 - y_i) \ln(1 - \hat{y_i})\right)
SoftJaccard = \frac{1}{n}\sum\limits_{i=1}^n\left(\frac{y_i\hat{y}_i}{y_{i}+\hat{y}_i-y_i\hat{y}_i}\right)
SoftJaccard=1n∑i=1n(yiy^iyi+y^i−yiy^i)SoftJaccard = \frac{1}{n}\sum\limits_{i=1}^n\left(\frac{y_i\hat{y}_i}{y_{i}+\hat{y}_i-y_i\hat{y}_i}\right)
LOSS = \alpha \times BCE + (1 - \alpha) \times SoftJaccard
LOSS=α×BCE+(1−α)×SoftJaccardLOSS = \alpha \times BCE + (1 - \alpha) \times SoftJaccard
CCE = - \frac {1} {n} \sum_{c=1}^7 \sum_{i=1}^{n} y_i^c \ln (\hat{y_i}^c)
CCE=−1n∑c=17∑i=1nyicln(yi^c)CCE = - \frac {1} {n} \sum_{c=1}^7 \sum_{i=1}^{n} y_i^c \ln (\hat{y_i}^c)
SoftJaccard =\frac{1}{n}\sum_{c=1}^7w_c\sum\limits_{i=1}^n\left(\frac{y_i^c\hat{y}^c_i}{y_{i}^c+\hat{y}^c_i-y_i^c\hat{y}_i^c}\right)
SoftJaccard=1n∑c=17wc∑i=1n(yicy^icyic+y^ic−yicy^ic)SoftJaccard =\frac{1}{n}\sum_{c=1}^7w_c\sum\limits_{i=1}^n\left(\frac{y_i^c\hat{y}^c_i}{y_{i}^c+\hat{y}^c_i-y_i^c\hat{y}_i^c}\right)
LOSS = \alpha \times CCE + (1 - \alpha) \times SoftJaccard
LOSS=α×CCE+(1−α)×SoftJaccardLOSS = \alpha \times CCE + (1 - \alpha) \times SoftJaccard
Jaccard
Public Test 0.636
Private Test 0.613
Jaccard
Public Test 0.493
Private Test 0.523
Made with Slides.com