Modeling the reliability of software developed in multiple releases
Vladimir Ivanov
Innopolis University
04/11/2016

Outline
- Overview of SRGM research
- Multi-stage SRGMs
- Data sets & Experiments
- Preliminary results
Software Reliability Growth Models (SRGM)
Overview and
the state of the art
Overview
According to ANSI, Software Reliability is defined as: the probability of failure-free software operation for a specified period of time in a specified environment. ["Standard Glossary of Software Engineering Terminology", STD-729-1991, ANSI/IEEE, 1991]
Usually, the reliability of software is measured as a number of defects or failures in a released software product or service.
Main applications:
- the optimal software release problem,
- the statistical testing-process control, and
- the optimal testing-effort allocation problem.
First models have been proposed decades ago
[J. D. Musa, A. Iannino, and K. Okumoto. Software reliability: measurement, prediction, application. McGraw-Hill, Inc., 1987]
Alan Wood. "Software reliability growth models".
Tandem Technical Report, 1996.
- Software reliability growth models can be used to provide reasonable predictions of the number of defects remaining in the field.
- Simple models perform as well or better than complex models.
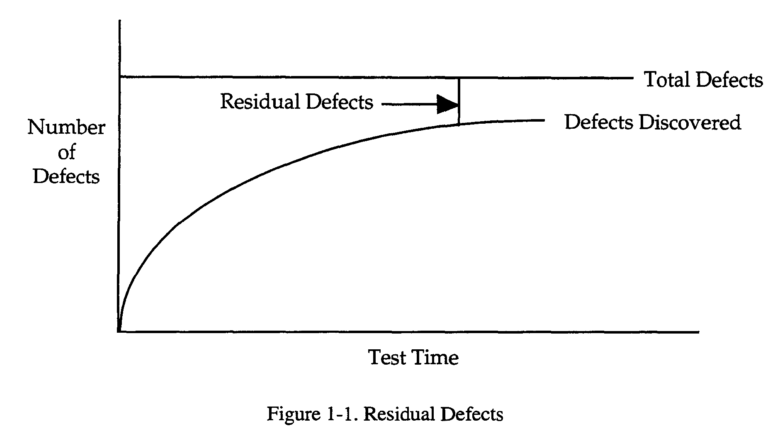
Basic SRGM
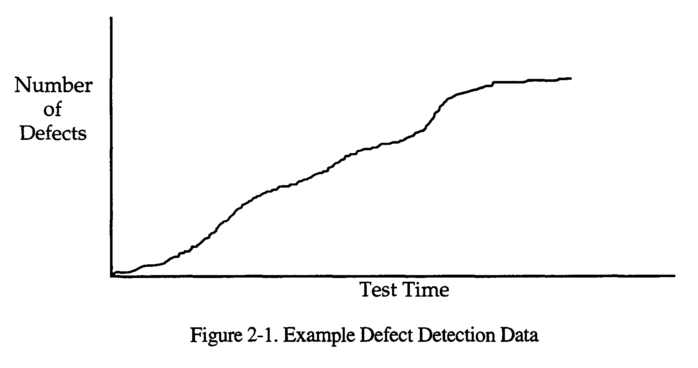
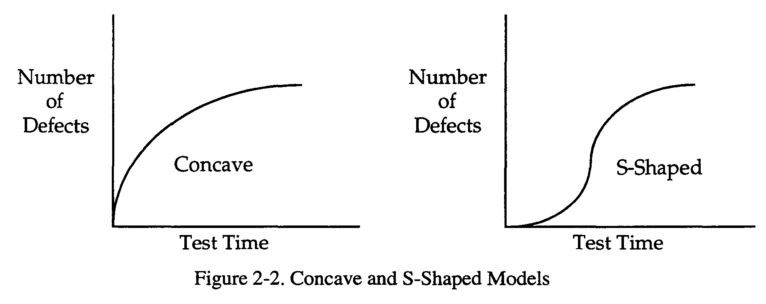

Multi-stage SRGM
Approach
-
A.G. Aggarwal, N. Nijhawan, and P.K. Kapur. A discrete SRGM for multi-release software system with imperfect debugging and related optimal release policy. In Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZE), 2015 International Conference on, pages 186–192, Feb 2015.
-
H. Aman, A. Yamashita, T. Sasaki, and M. Kawahara. Multistage growth model for code change events in open source software development: An example using development of Nagios. In Software Engineering and Advanced Applications (SEAA), 2014 40th EUROMICRO Conference on, pages 207–212. IEEE, 2014.
-
P. K. Kapur, H. Pham, A. G. Aggarwal, and G. Kaur. Two Dimensional Multi-Release Software Reliability Modeling and Optimal Release Planning. IEEE Transactions on Reliability, 61(3):758–768, 2012.
- Q. P. Hu, R. Peng, M. Xie, S. H. Ng, and G. Levitin. Software Reliability Modelling and Optimization for Multi-release Software Development Processes. 2011 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), pages 1534–1538, 2011.
Recent studies in Multi-stage SRGM
(2011 - ...)

Recent studies in Multi-stage SRGM
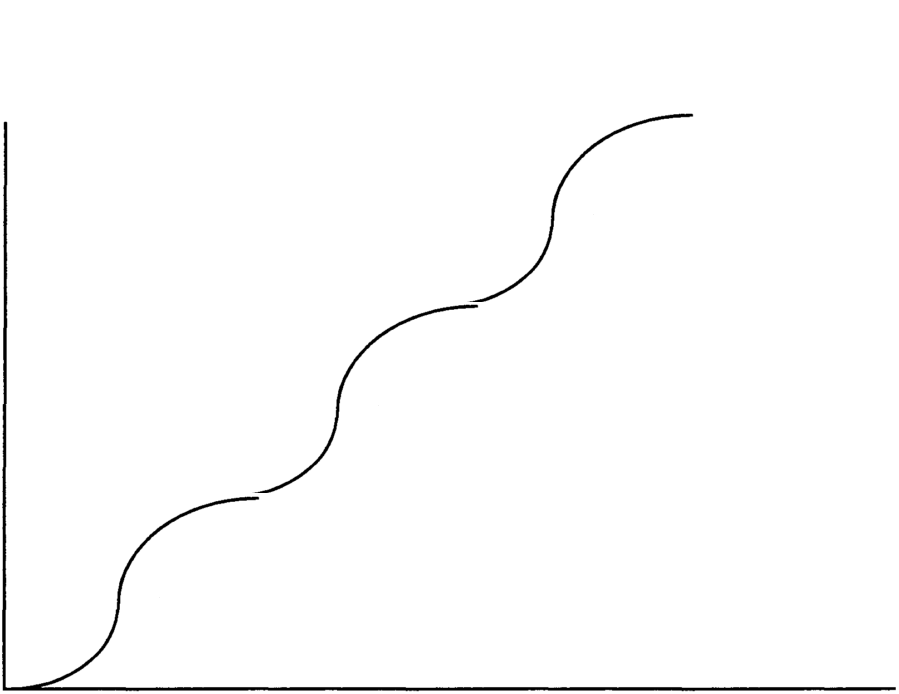
- We assume that during testing several portions of software could be released.
- Hence, data that describe a process of bug arrival may be better described as a summation of basic SRGMs for the individual releases.
Approach
a basic SRGM
- Let n be a number of releases
-
Approach
a basic SRGM;
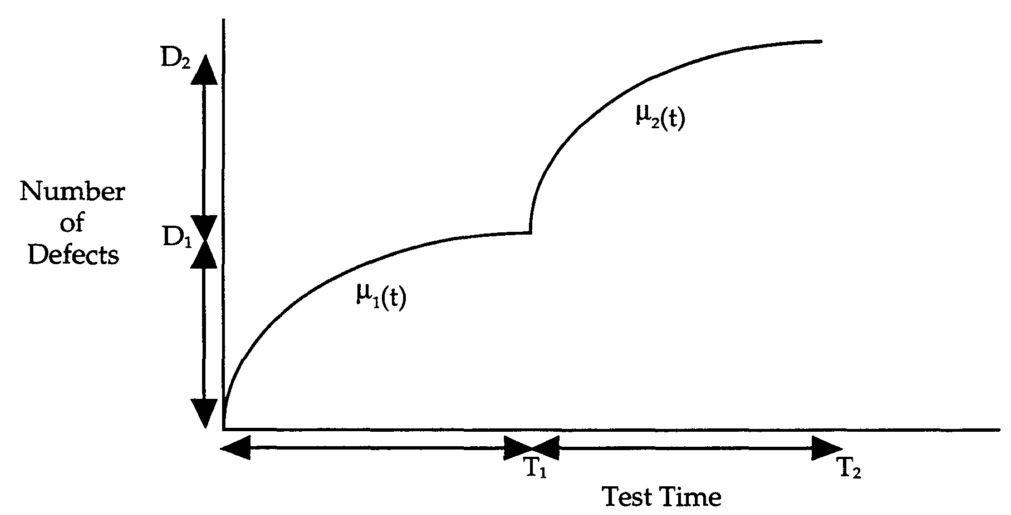
bugs in the i-th release
time of the i-th release
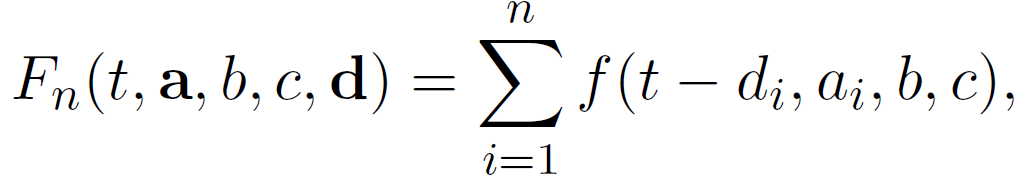
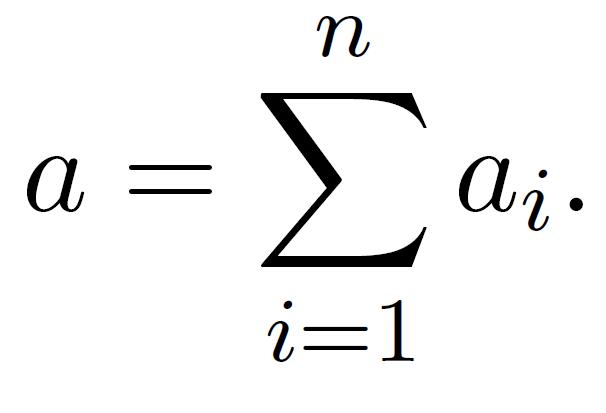
n-release SRGM will depend on 4n parameters
We simplify it by an assumption
We got a model with 2n+2 parameters
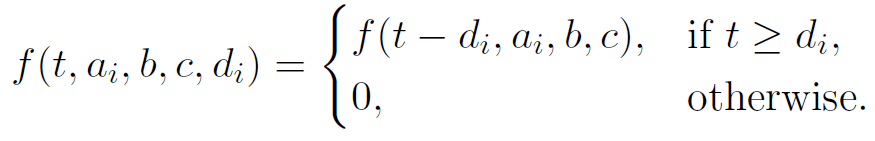
Fitting a curve to the Data
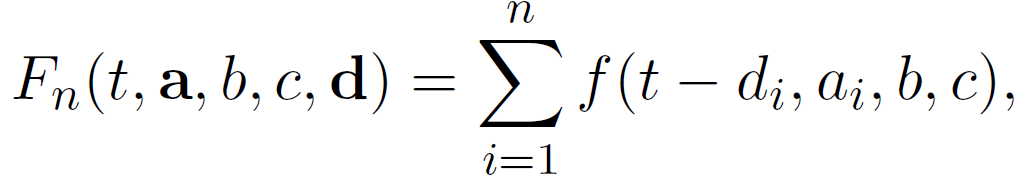

- A nonlinear regression problem
- Levenberg-Marquart method
Data sets and Experiments
Two complementary goals:
- characterize development processes
- predict left-over bugs
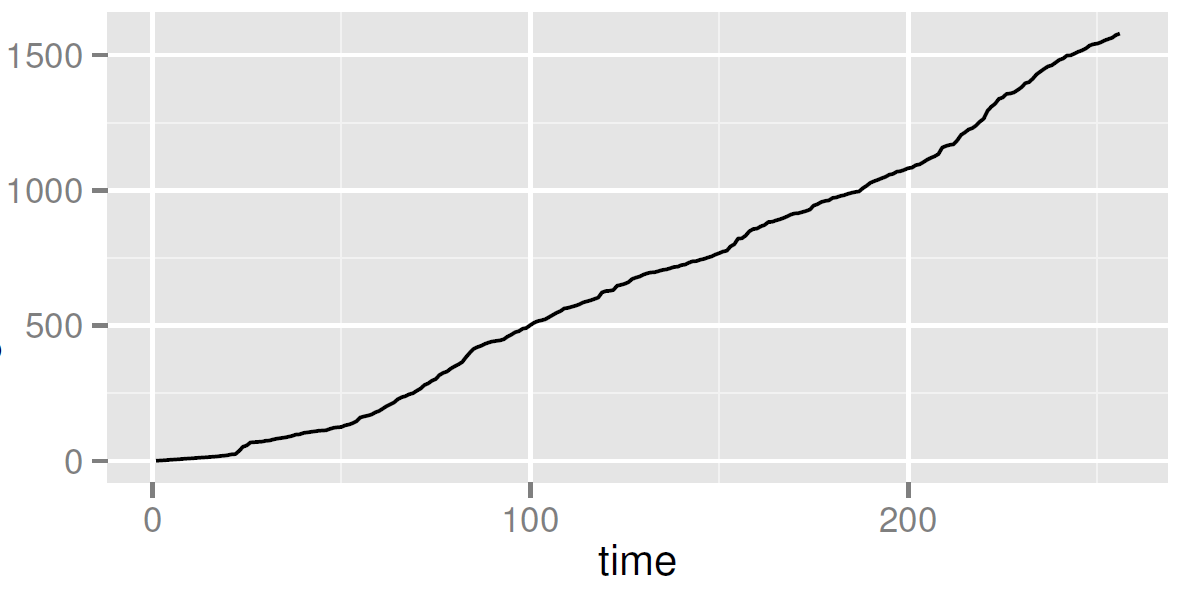
Data
8 Data sets of bug arrivals of two types:
- Open source OS: CyanogenMod, TIZEN, Sailfish (x2)
- Commercial product (4 versions)
Metrics
- Goodness of Fit (GoF),
- Relative Precision of Fit (RPoF),
- Coverage of Fit (CoF),
- Prediction Power (PPow),
- Accuracy of Final Point (AcFP).
The goodness of fit (GoF)
is the root mean square evaluation of how well
the model fits the original data. The unit used for goodness of fit is the
number of MRs.
The relative precision of fit (RPoF)
is the area of the bootstrap 95%
confidence interval of the stripe of the model, normalized over the analyzed
time. Therefore, models with low value of the
relative precision of fit typically have high capability of providing useful
information about the occurrence of SRs.
The coverage of fit (CoF)
is degree to which the bootstrap 95% confidence
interval of the stripe of the model captures the observed MRs. The unit
used for the coverage of fit is the fraction of the total number of MRs within
the bootstrap 95% confidence interval. model. It is measured in
percentages.
Prediction Power (PPow)
shows how early in the development the model
is able to predict the final number of defects with maximum 10% error.
calculated as a relative error between the value
of actual number of bugs and the predicted by the
Accuracy
of Final Point (AcFP)
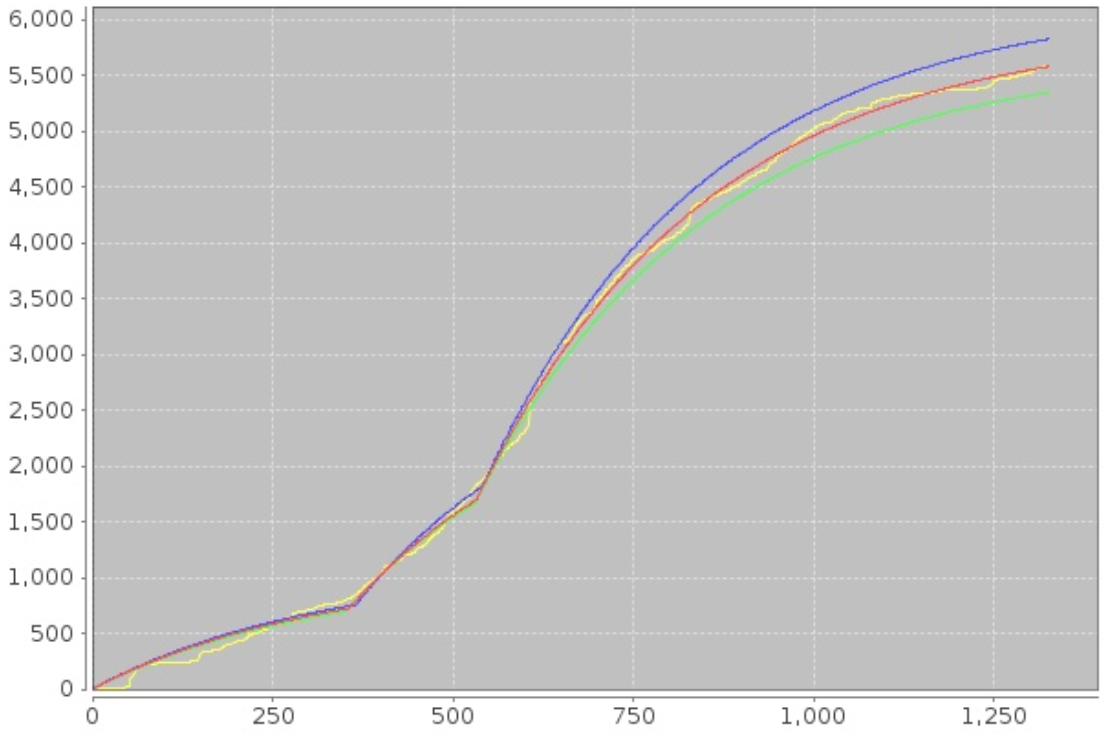
Bootstrapping (80% of data, no returns)
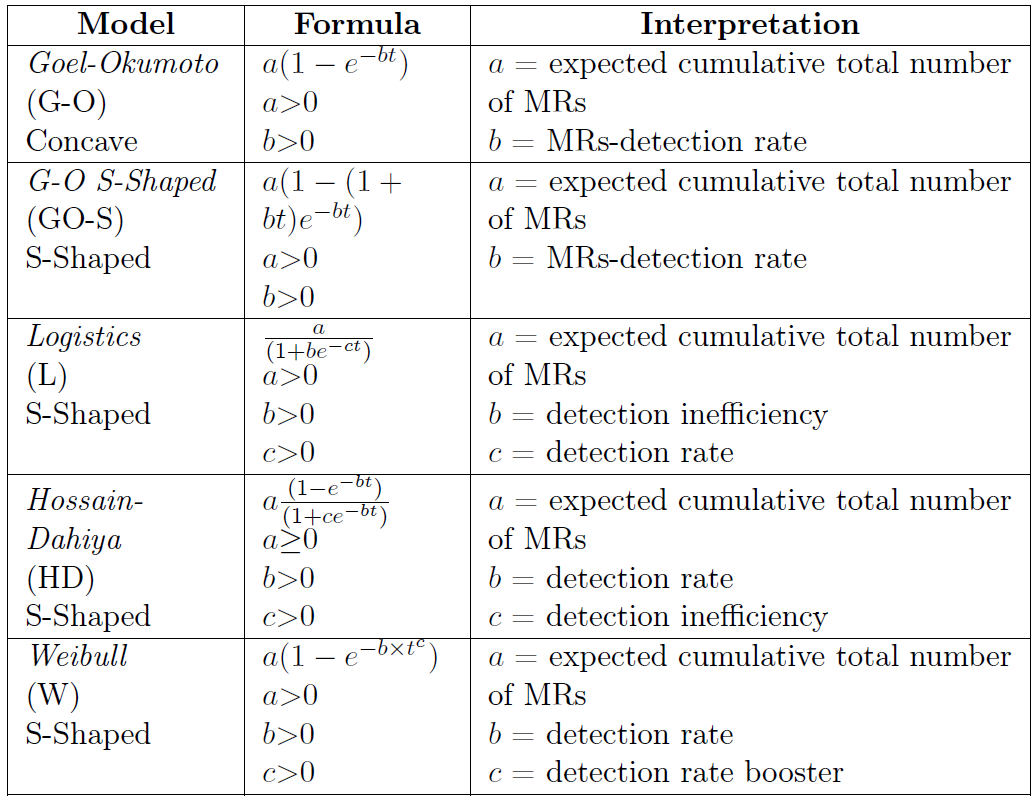
Models
- Goel-Okumoto
- Goel-Okumoto (GO-S)
- Logistics (L)
- Hossain-Dahiya (HD)
- Weibull (W)
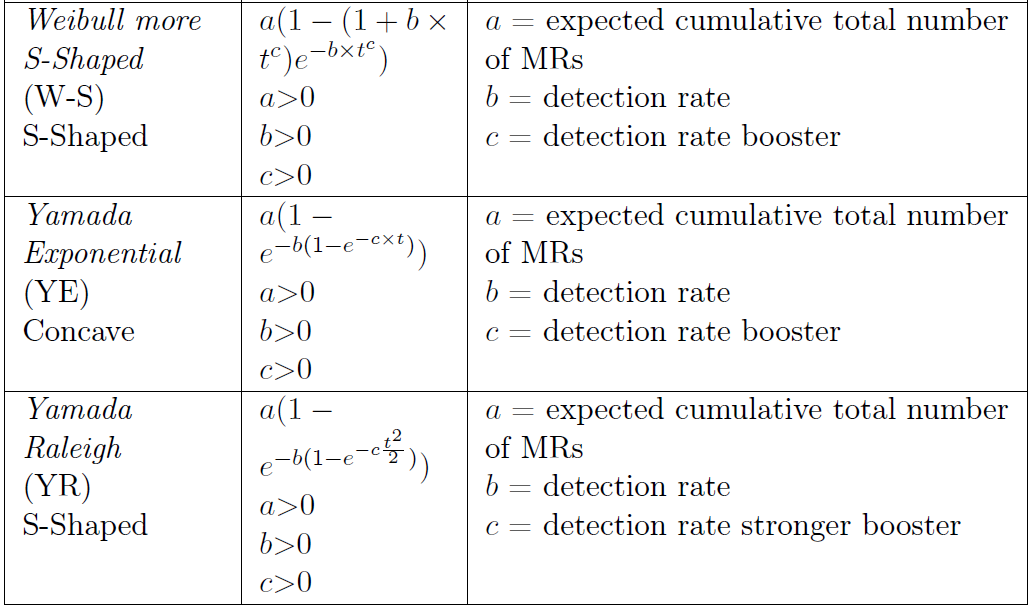
- Weibull more S-Shaped (W-S)
- Yamada Exponential (YE)
- Yamada Raleigh (YR)
Results
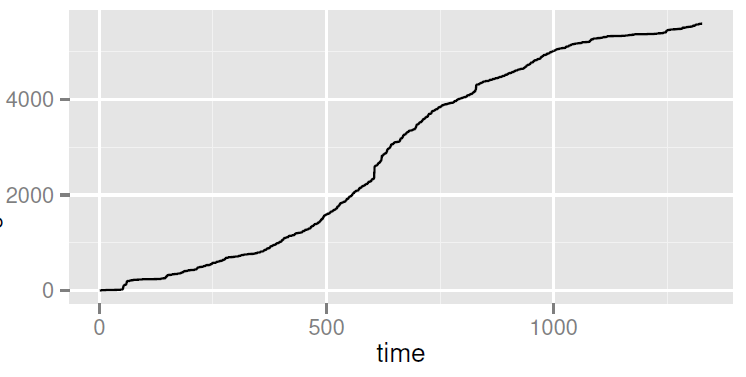
Sailfish-Nemo, n=4, GOS Model
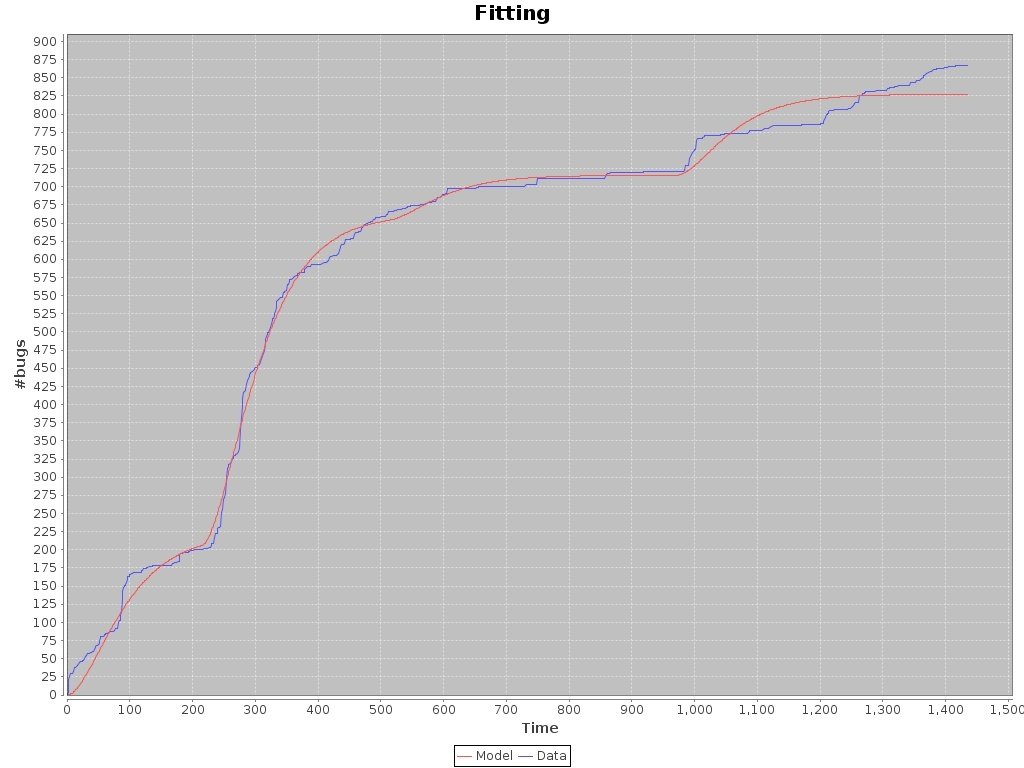
Sailfish-Nemo, n=14, GOS Model
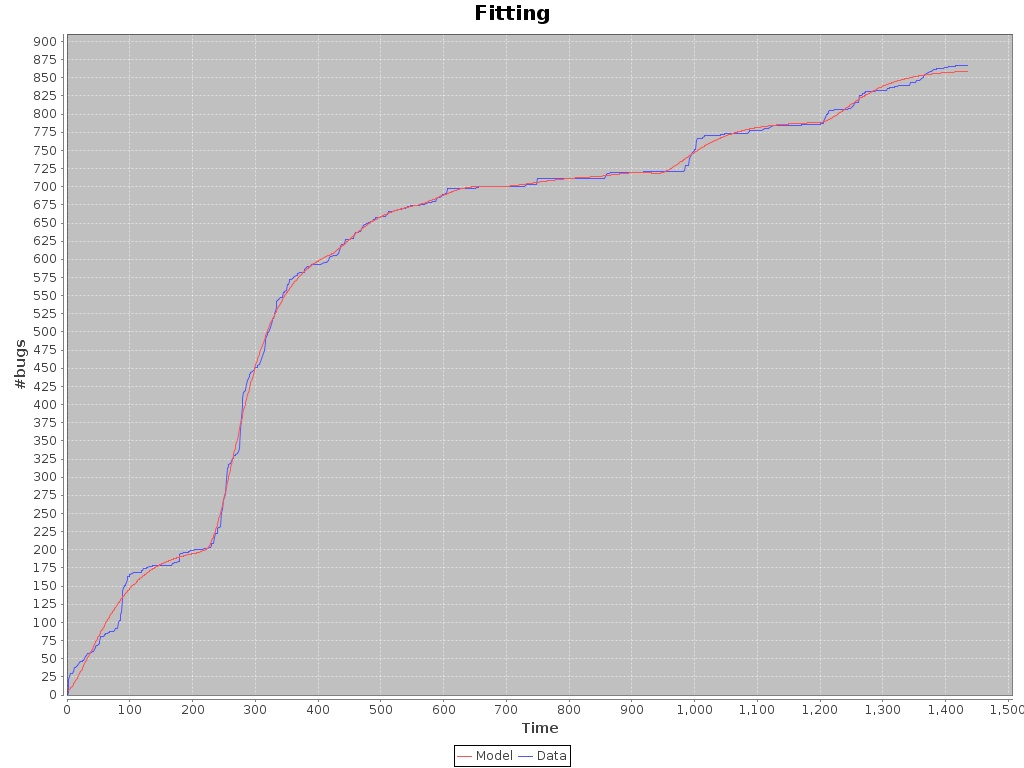
Sailfish-Nemo, n=20, GOS Model


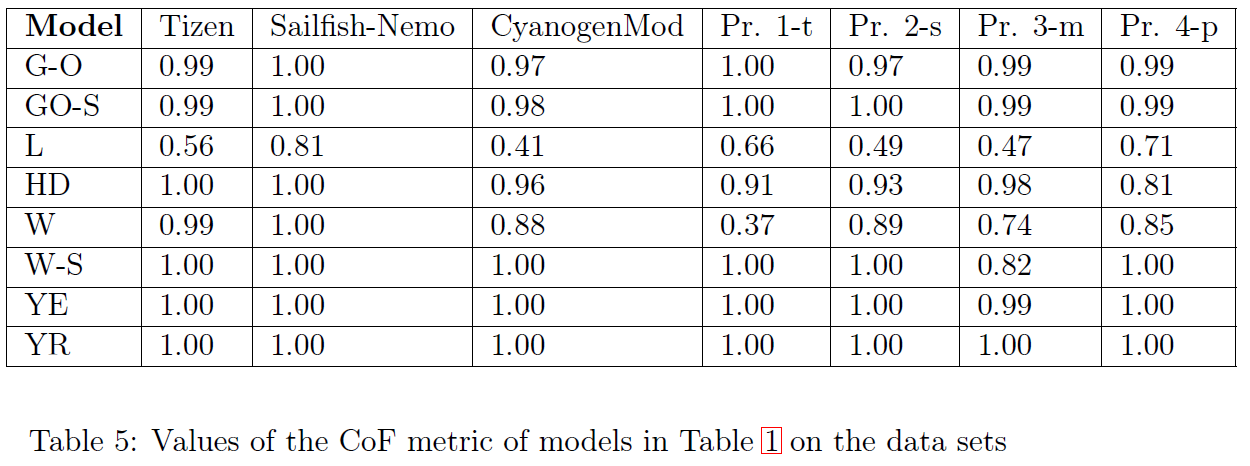
Model comparison
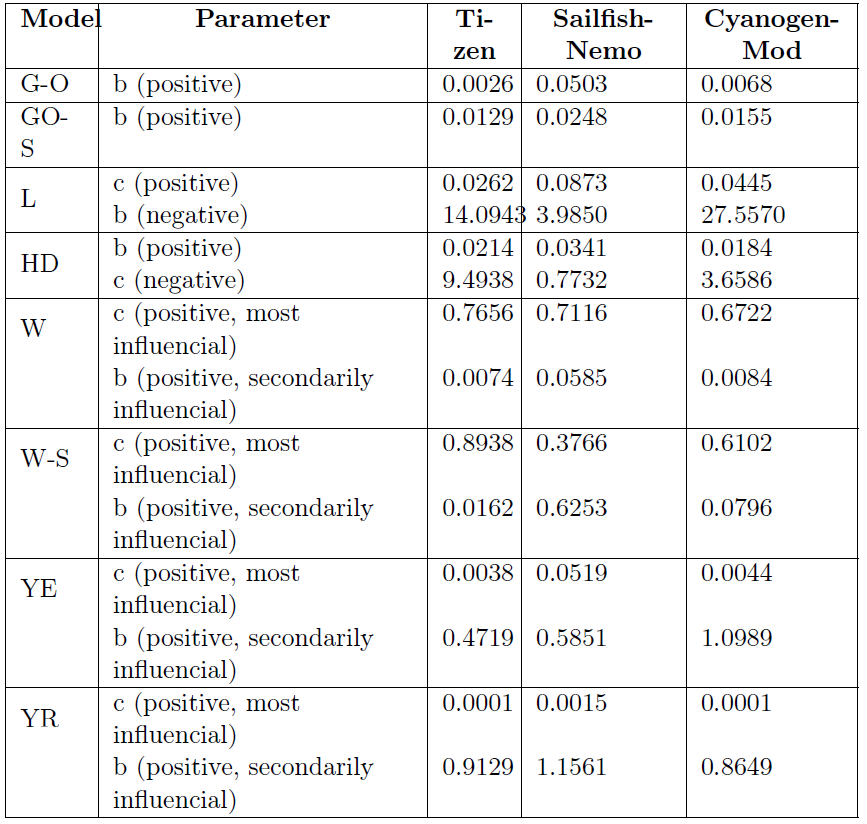
Analysis of testing using additional parameters
Results for Mobile OS
are available
Thank you for your attention!