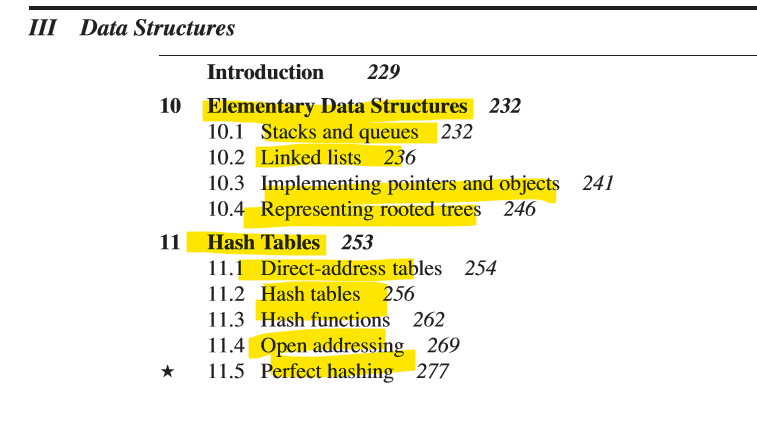
Algorithms #14
Conclusion

What have we learned ?

Overview
of usecases
1. Google maps & Dijkstra algorithm and weighteg graph
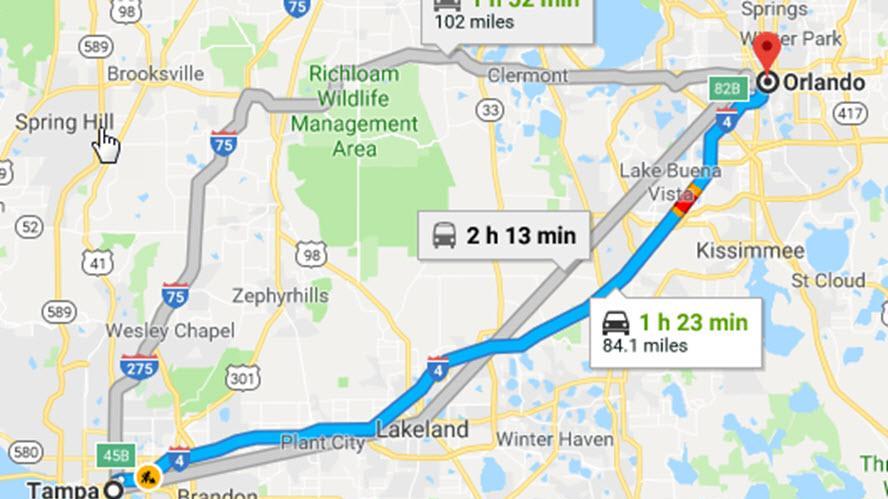
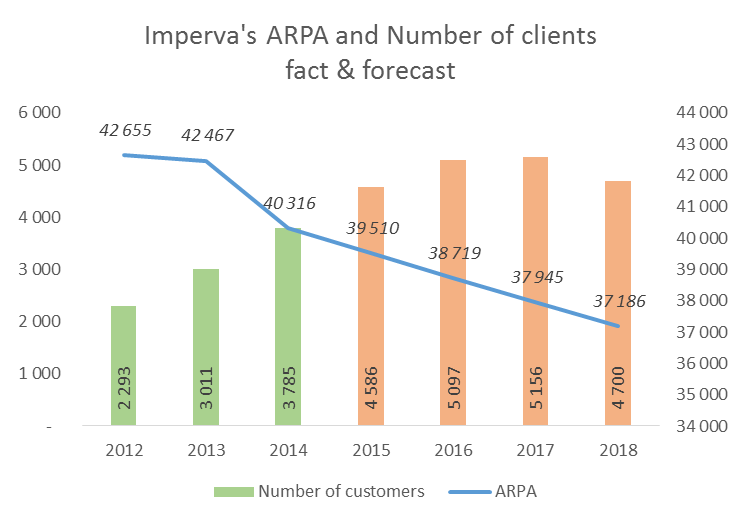
2. How companies optimizing expenses via DP methods
3. Common substrings algorithm which is used in git diff & merge. (And in biology DNA compare)

4. How recommendation systems and social networks use graphs
5. How OS works with process prioryty using Heap & Priority Queue

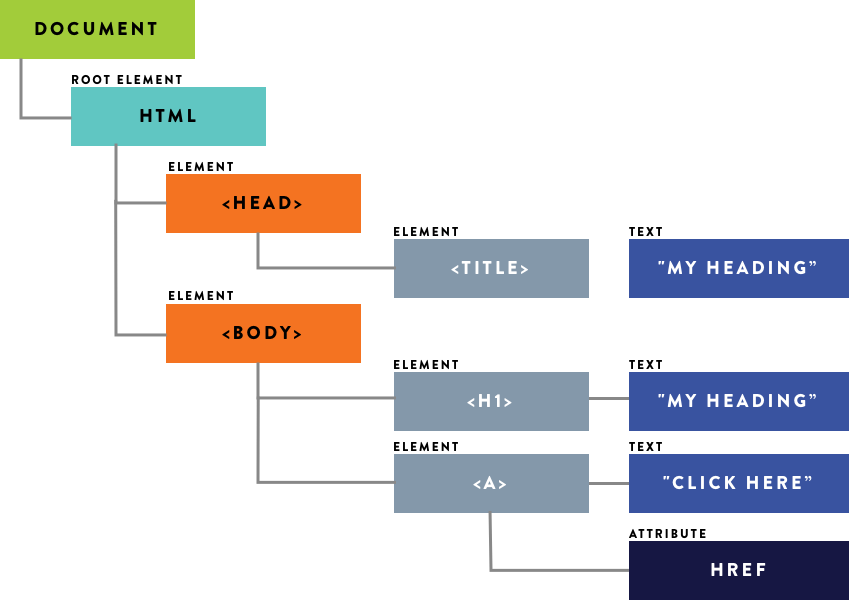
6. DOM internal Tree structure organisation
7. How hashing & HashMap works. Which gives great boost in different in-memory DB stores.

8. Stack & Queue. Which are used everywhere (For ex. browser history)
9. Different ways of searching and sorting data in the collections

10. General approaches for solving any algorithm problem
Frequency Counter Pattern
Two Pointers
Window Sliding
Divide and Conquer
And many more!







So should a programmer learn and know ?
An algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform the input into the output.
Let us first refresh what an algorithm is...

Isn't this is something, that any programmer does everyday ?
Should a programmer know advanced algorithms ?
Lets rephrase it
Depends on the goals
Forms,
CRMs
REST services
etc.
NO
YES

New revolutionary products & platforms,
science,
devices
So do you want to be a true engineer or a coder ?


You not learning algorithms, you learning techniques, which will help you to solve your task more efficiently

Knowing algorithms will help you:
- Find patterns in problems and solving them efficiently.
- It will make you super fast especially in the easy/medium level problems
- Choosing the right technique/data structure is a basic skill when you start learning algorithm and practice solving problems
- Analyse your solution and understand why it should work based on the amount of input data you expect .. or may be understand why a solution won’t work …
- Reducing some problems to be able to use a specific programming techniques
- How to store your data efficiently for later processing
- When to do pre-processing for your data to minimize the running time of later hits to your data
- When you use technologies that does Caching/Hasing/Indexing/… you will know how these things work internally and this will make you a better user of the tech
But everything is already implemented in libraries and frameworks ?
- Think about size of your application if you are going to add a library for every little problem
- Some frameworks require you to add application specific settings
- Developers who can solve a problem only with a library are not in demand on the market
- In any case you should know how the library doing the job, to understand if it feats you application needs
What we didn't cover ?

Greedy algorithms
Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to global solution are best fit for Greedy.
We didn't cover
Or may be we did ?
Greedy algorithm problem example
Coin change problem
The problem at hand is coin change problem, which goes like given coins of denominations 1,5,10,25,100; find out a way to give a customer an amount with the fewest number of coins.
Amount: 30
Solutions : 3 X 10 ( 3 coins )
6 X 5 ( 6 coins )
1 X 25 + 5 X 1 ( 6 coins )
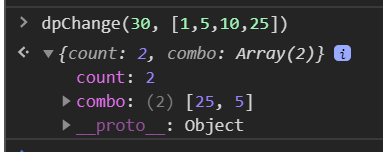
1 X 25 + 1 X 5 ( 2 coins )Isn't this a Dynamic Programming problem ?
Coin change problem : Algorithm
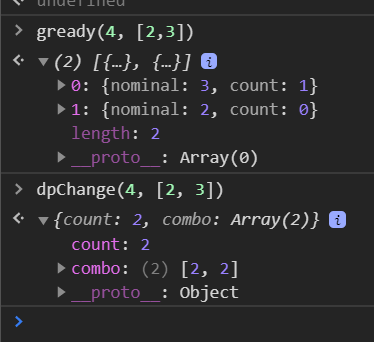
const nominals = [1, 5, 10, 25];
function gready(amount, nominals) {
let res = [];
let totalAmount = amount;
for(let i = nominals.length - 1; i >= 0; i--) {
const coinValue = nominals[i];
const typeCount = Math.floor(totalAmount / coinValue );
res.push({ nominal: coinValue, count: typeCount });
totalAmount -= ( typeCount * coinValue);
}
return res;
}
A dynamic programming approach
function dpChange(amount = 5, nominals = [1, 5]) {
const cache = [ { count: 0, combo: [] } ];
for(let curr of nominals) {
for(let i = 1; i <= amount; i++) {
let minPossible = { count: Infinity };
if (curr <= i) {
const left = cache[i - curr]
const cand = left.count + 1;
if (cand < minPossible.count) {
minPossible = { count: cand, combo: [curr, ...left.combo] }
}
}
if (!cache[i] || cache[i].count > minPossible.count) {
cache[i] = minPossible;
}
}
}
return cache[amount]
}
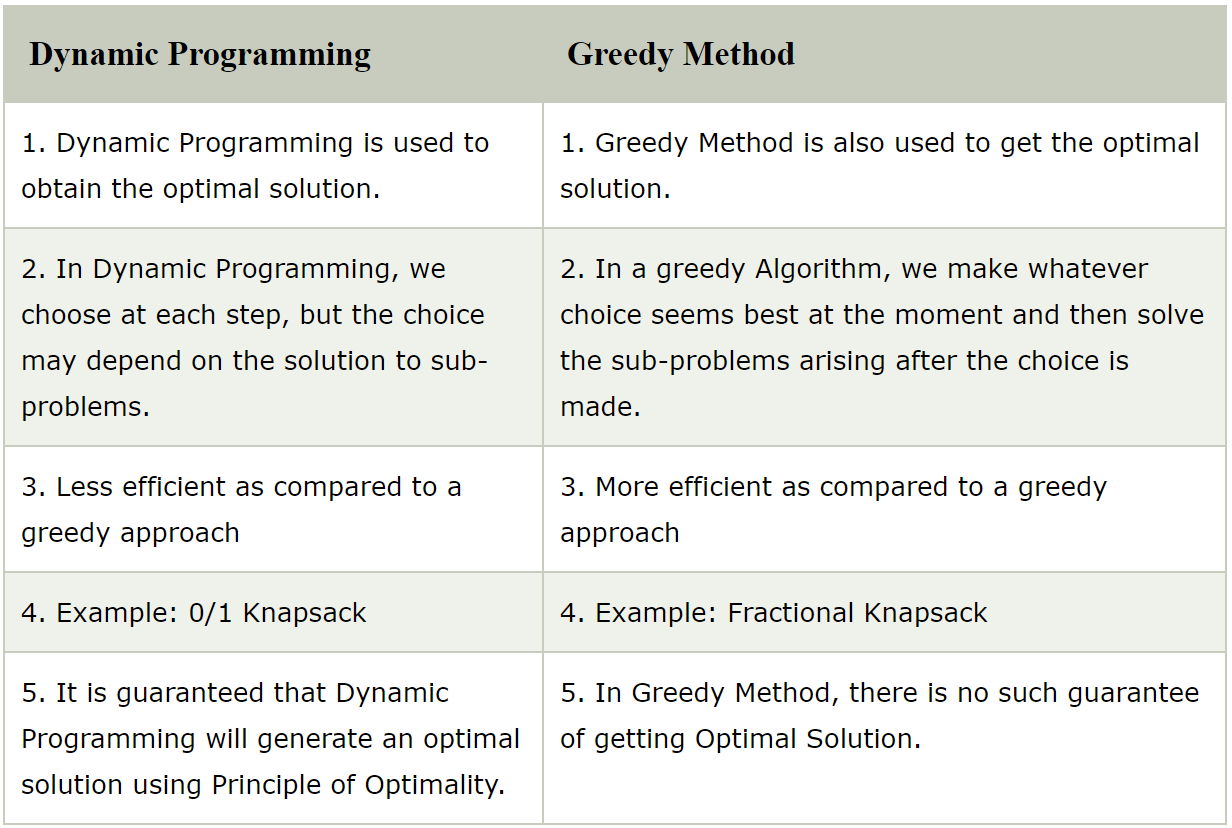
What's the difference between greedy algorithm and dynamic programming?
A Greedy algorithm is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit.
Typical problems
NP-completeness

NP - nondeterministic polynomial
In Theoretical Computer Science, the two most basic classes of problems are P and NP
P includes all problems that can be solved efficiently. For example: add two numbers. The formal definition of "efficiently" is in time that's polynomial in the input's size.
NP includes all problems that given a solution, one can efficient verify that the solution is correct

There are optimization problems associated with several of the NP-complete problems that we have encountered. Here are a few.
Traveling Salesman Optimization Problem. Given a distance matrix, find the shortest traveling salesman tour.
Maximum Clique Problem. Given an undirected graph G, find a largest possible clique in G.
Min-Color Problem. Given an undirected graph G, color the vertices G with the fewest possible colors, ensuring that no two adjacent vertices have the same color.
Longest Path Problem. Given an undirected graph G and two vertices u and v, find a longest simple path from u to v.
All of those problems are NP-hard. Each one is closely related to a known NP-complete problem. Let's take the Maximum Clique problem (MAX-CLIQUE) as an example. CP is the Clique problem.
NP-hard problems are often tackled with rules-based languages in areas including:
- Approximate computing
- Cryptography
- Data mining
- Decision support
- Phylogenetics
- Planning
- Process monitoring and control
- Rosters or schedules
- Routing/vehicle routing
Also we didn't talk about:
1. Prime numbers
Prime number is important when it comes to Cryptography. Specially RSA algorithm. This is because to hack it a common method is to use addition subtraction, and other elementary operators which can be difficult with prime number codes.
AKS algorithm
2. Bitwise Algorithms
The Bitwise Algorithms are used to perform operations at bit-level or to manipulate bits in different ways. The bitwise operations are found to be much faster and are some times used to improve the efficiency of a program.
- Find the element that appears once
- Detect if two integers have opposite signs
- Add 1 to a given number
- Multiply a given Integer with 3.5
- Turn off the rightmost set bit
- Find whether a given number is a power of 4 or not
- Compute modulus division by a power-of-2-number
- Rotate bits of a number
- Find the Number Occurring Odd Number of Times
- Check for Integer Overflow
- Count set bits in an integer
- Count number of bits to be flipped to convert A to B
3. String matching algorithms
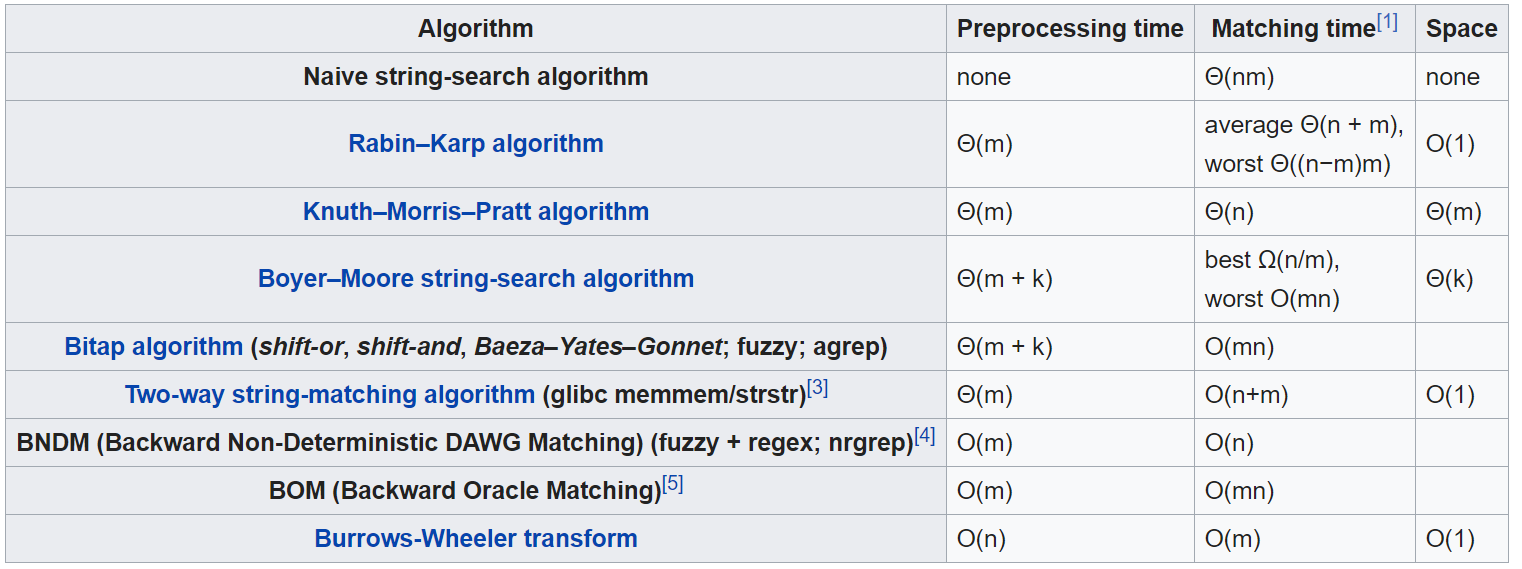
And much more!

But nevertheless
Non IT person
everage
outsource developer
You after compleating and (realizing/practicing) the cource
What should be your goal
Ability to solve complex problems graph
Whats next ?

Introduction to Algorithms, 3rd Edition (The MIT Press)


Cracking the Coding Interview: 189 Programming Questions and Solutions
Also
And also ofc


Never Stop Improving !
Thank you!
