Algorithms #4

Sorting

Sorting algorithm

A sorting algorithm is an algorithm made up of a series of instructions that takes an array as input, performs specified operations on the array, sometimes called a list, and outputs a sorted array. Sorting algorithms are often taught early in computer science classes as they provide a straightforward way to introduce other key computer science topics like Big-O notation, divide-and-conquer methods, and data structures such as binary trees, and heaps.

There are many factors to consider when choosing a sorting algorithm to use.

Sorting Algorithms

Comparison Sorts

Integer Sorts

Also sort algorithm can be stable and not stable

Sorting Algorithms :

Visualization

Simplest sorting algorithm

Bubble Sort

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.

Bubble Sort

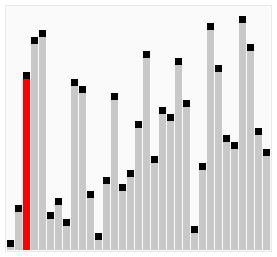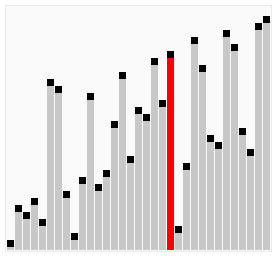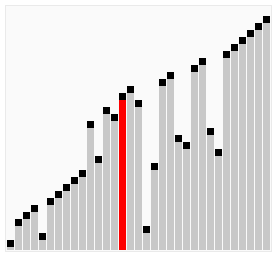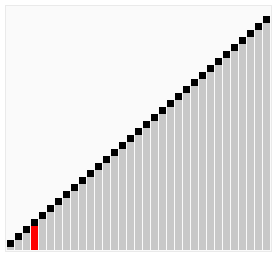
Worst and Average Case Time Complexity: O(n*n). Worst case occurs when array is reverse sorted.

Best Case Time Complexity: O(n). Best case occurs when array is already sorted.

Auxiliary Space: O(1)

Boundary Cases: Bubble sort takes minimum time (Order of n) when elements are already sorted.

Sorting In Place: Yes

Stable: Yes

Bubble Sort Implementation

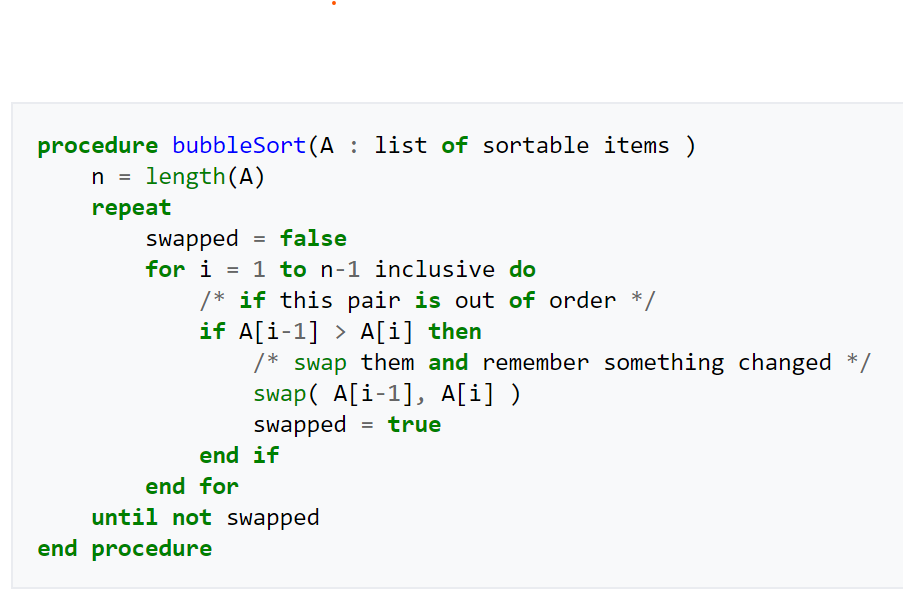
Bubble Sort

Problem #1

Write a function to generate random numbers array given length
Write a function to generate random sorted array
Write a function to generate random almost sorted array

Problem #2

Implement bubble sort

Problem #3

Write a function to check running time of other function with given arguments:

checkRunningTime(bubbleSort, [10,20,0,1]) // 0.001 ms

Check running time of bubble sort with 1000, 10000 and 100000 size arrays, sorted and unsorted

Selection sort

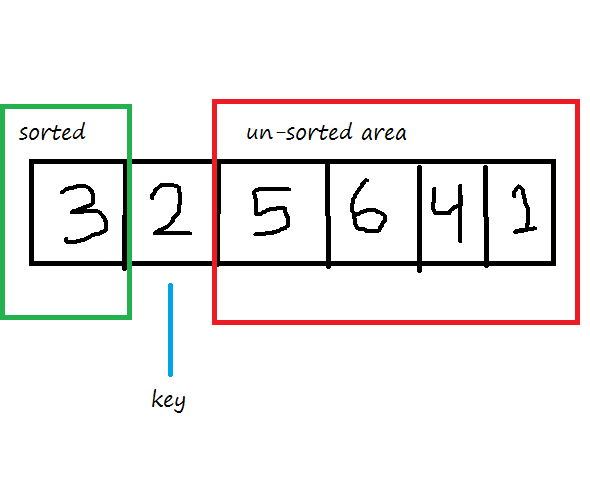
The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from unsorted part and putting it at the beginning. The algorithm maintains two subarrays in a given array.

1) The subarray which is already sorted.
2) Remaining subarray which is unsorted.

In every iteration of selection sort, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.

Selection sort

Time Complexity: O(n2) as there are two nested loops.

Auxiliary Space: O(1)
The good thing about selection sort is it never makes more than O(n) swaps and can be useful when memory write is a costly operation.

Stability : The default implementation is not stable.
However it can be made stable. Please see stable selection sort for details.

In Place : Yes, it does not require extra space.

Problem #4

Implement selection sort

Insertion sort

Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands.

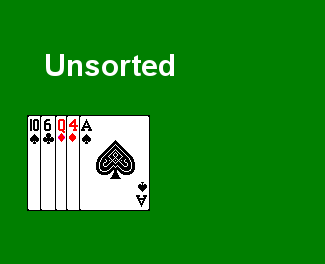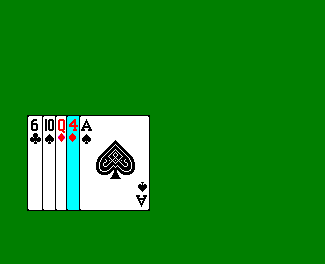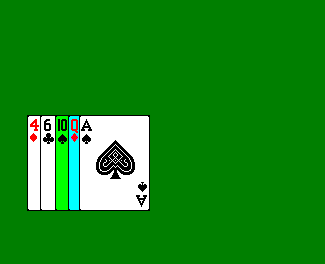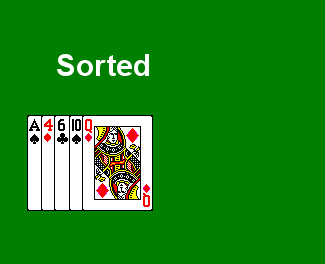
Insertion sort

Time Complexity: O(n^2)

Auxiliary Space: O(1)

Boundary Cases: Insertion sort takes maximum time to sort if elements are sorted in reverse order. And it takes minimum time (Order of n) when elements are already sorted.

Algorithmic Paradigm: Incremental Approach

Sorting In Place: Yes

Stable: Yes

Insertion sort

Problem #5

Implement insertion sort

What is Binary Insertion Sort?

We can use binary search to reduce the number of comparisons in normal insertion sort.

Binary Insertion Sort uses binary search to find the proper location to insert the selected item at each iteration. In normal insertion, sorting takes O(i) (at ith iteration) in worst case. We can reduce it to O(logi) by using binary search. The algorithm, as a whole, still has a running worst case running time of O(n2) because of the series of swaps required for each insertion. Refer this for implementation.

Thank you!

Links

https://www.geeksforgeeks.org/stability-in-sorting-algorithms/ - Stability in sorting algorithms

https://en.wikipedia.org/wiki/Online_algorithm - Online algorithm

https://www.geeksforgeeks.org/in-place-algorithm/ - In-Place Algorithm

https://brilliant.org/wiki/sorting-algorithms/ - Sorting Algorithms overview