Algorithms #7

Stack & Queue

Stack

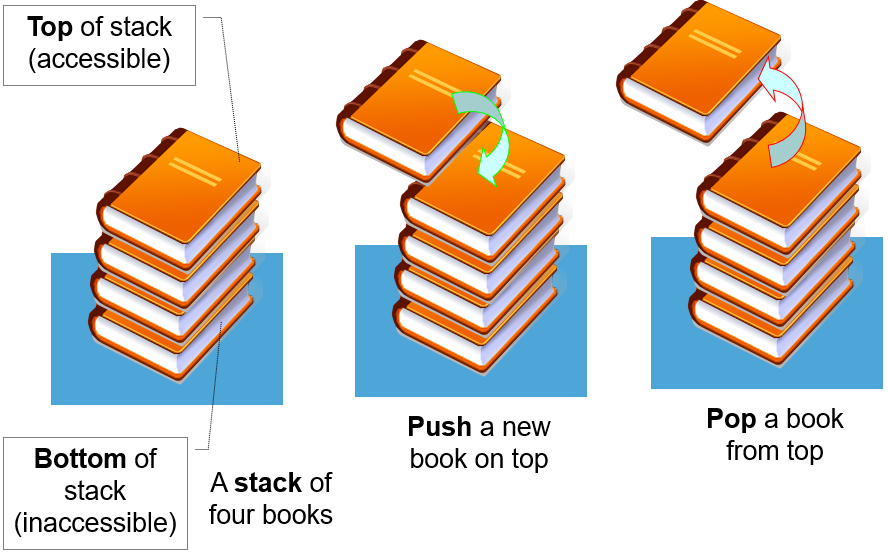
Stack is a linear data structure which follows a particular order in which the operations are performed.

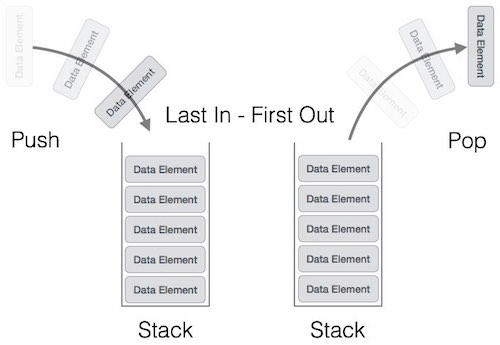
Stack LIFO

The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out)

Stack operations

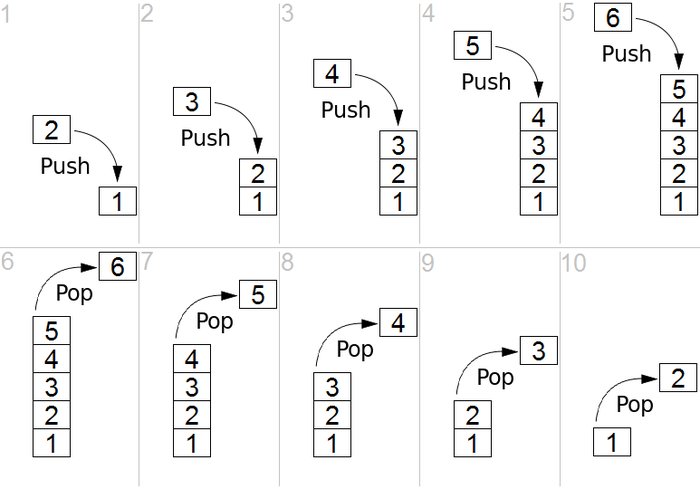
push(x) places the item x onto the top of the stack

pop() removes the top item from the stack, and returns that item.

Usages of Stack

DFS (Depth First Search) on tree / graph datastructures
During Function Calls (Call Stack in JS)
AST processing / Syntax parsing
Browser back-forth button (JS History API).
Reversing a string
Converting expressions(prefix-infix-postfix)
Recursive functions.
Maintaining any sort of LIFO data.
And many more...

Problem #1

Implement string stack using only string operations

const stack = new StringStack();
stack.push("one");
stack.push("two");
stack.push("three");

stack.pop() // three

Problem #2

Implement string stack using linked list

const stack = new Stack();
stack.push("one");
stack.push("two");
stack.push("three");

stack.pop() // three

Problem #3

Implement string stack using linked list

function validateBrackets(ext) {
 ...
}

validateBrackets("[(1 + 1)]^2"); // true 
validateBrackets("(1 + [2 *) - 1]"); // false
validateBrackets("({[]})"); // true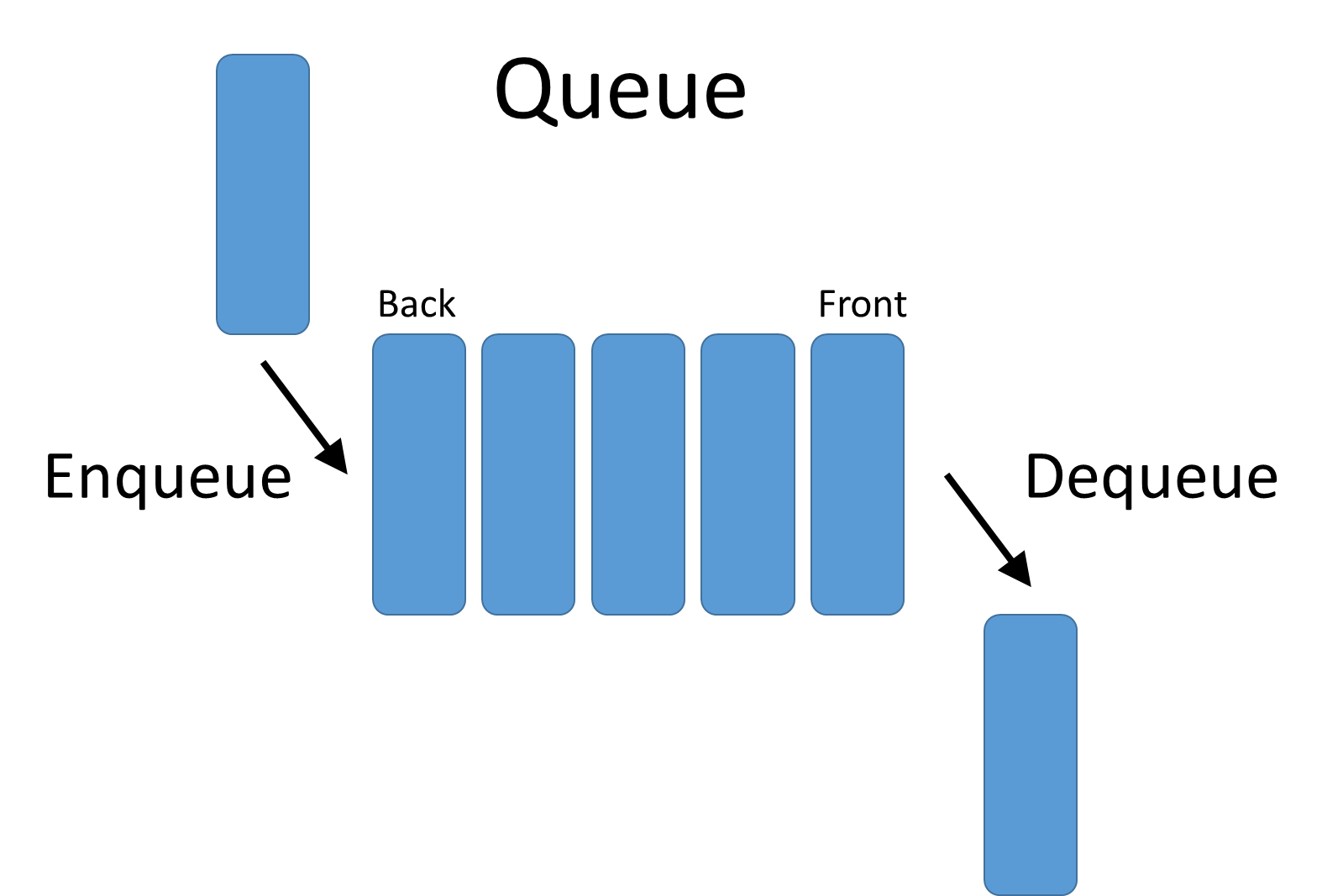

Queue is a linear data structure where the first element is inserted from one end called REAR and deleted from the other end called as FRONT. (FIFO)

enqueue()	This function defines the operation for adding an element into queue.
dequeue()	This function defines the operation for removing an element from queue.
	Pointers
Front	Front is used to get the front data item from a queue.
Rear	Rear is used to get the last item from a queue.

Queue interface

Queue uses

Asynchronous data transfer (file IO, pipes, sockets)
Simulation of real-world queues such as lines at a ticket counter or any other first-come first-served scenario requires a queue.
BFS (Breadth First search) in a Graph. It is an algorithm for traversing or searching graph data structures. It starts at some arbitrary node of a graph and explores the neighbor nodes first, before moving to the next level neighbors.This Algorithm uses Queue data structure.
Handling of interrupts in real-time systems. The interrupts are handled in the same order as they arrive, First come first served.
Etc

Problem #4

Implement queue using linked list

Problem #5

1. Implement queue using stack API only
2. Implement stack using queue API only

Problem #6

Implement priority queue

const queue = new PriorityQueue();

queue.enqueue("one", 10);
queue.enqueue("two", 10);
queue.equeue("truee", 1);

queue.dequeue() // "three";
queue.dequeue() // "one"