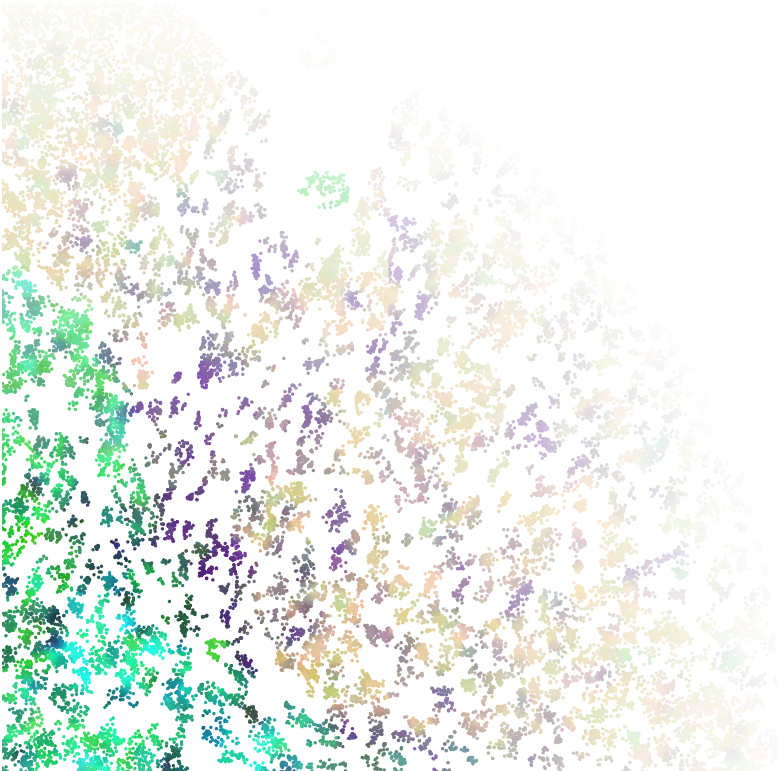
Boundary detection

V. Petukhov, P. Kharchenko

Goal

Estimate

boundaries

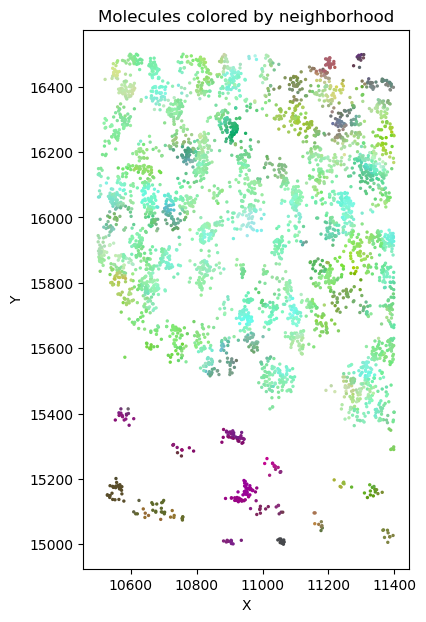
Set of molecules

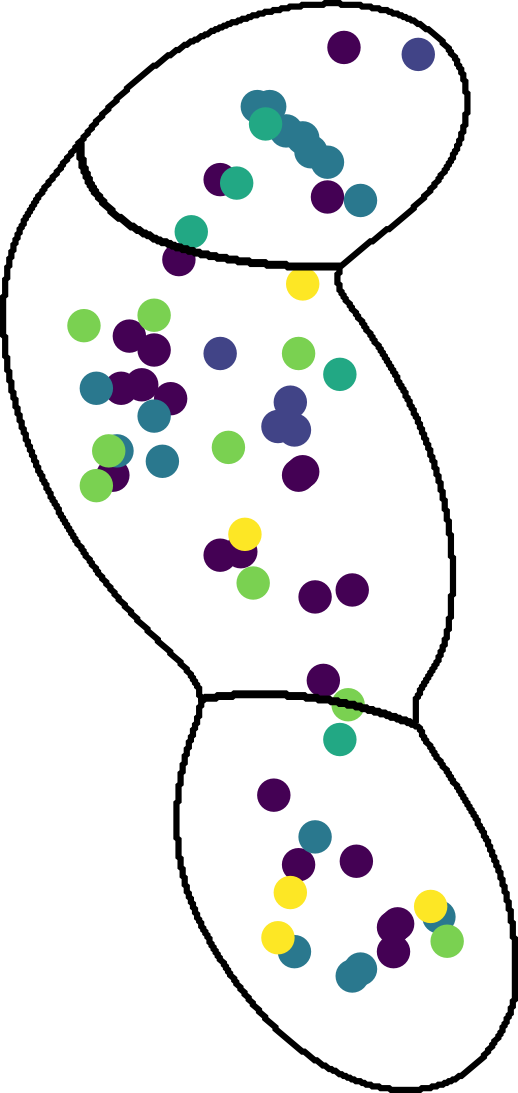
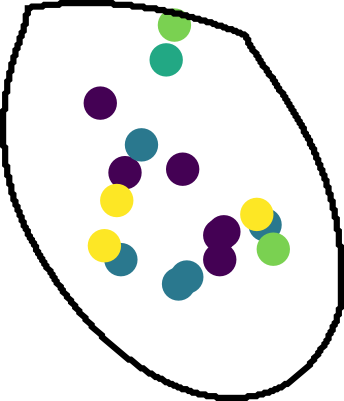
Split molecules by cells

Basic idea

X	Y	Gene
...	...	...

We know:

What is the source?

Gene 1: 20%

Gene 2: 80%

Gene 1: 80%

Gene 2: 20%

Basic idea

Gene 1	...	Gene k
N1		Nk

Gene vector

Embedding to 3d space

k nearest

neighbors

Model description

Global scale

Cell type

Shape / size

Position of center

scRNA-seq data

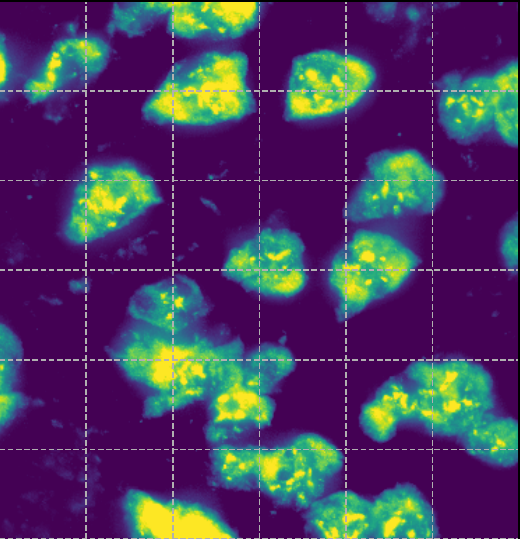
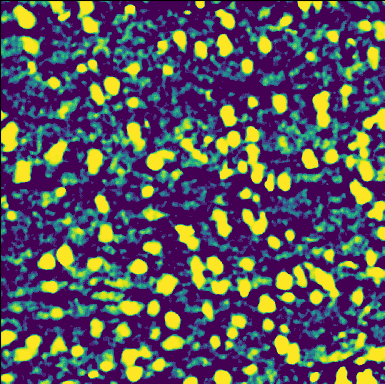
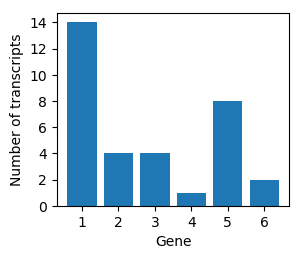
Composition

Nuclei stains

Membrane stains

Molecules

Boundaries

Model description

Transcript composition

Center position, ellipsoid shape

2D Normal distribution

Multinomial distribution

0.43

0.12

0.03

0.24

0.06

3.5	-1.5
-1.5	3.5

\Sigma:

\Sigma:

M:

Position

Shape

Composition

P:

Cell is a distribution:

f(x, y, g) = N(x, y | M, \Sigma) P(g)

f(x, y, g) = N(x, y | M, \Sigma) P(g)

Goal v2.0

Separate probability distributions from a mixture model

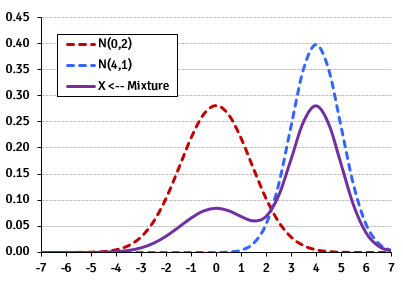
EM on spatial data

Algorithm v0.01

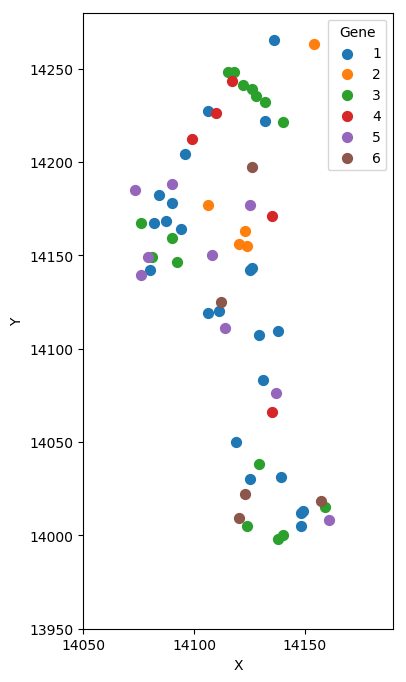
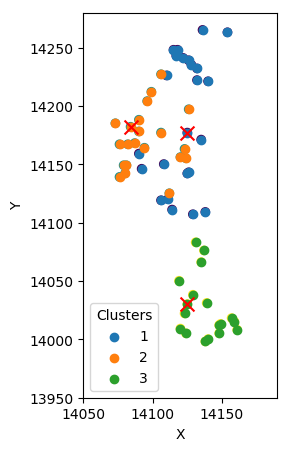
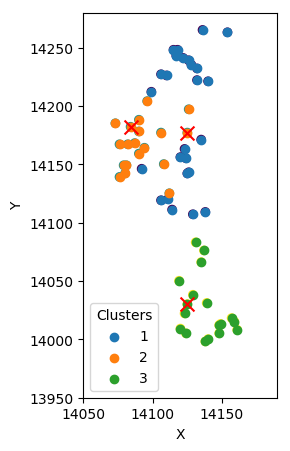
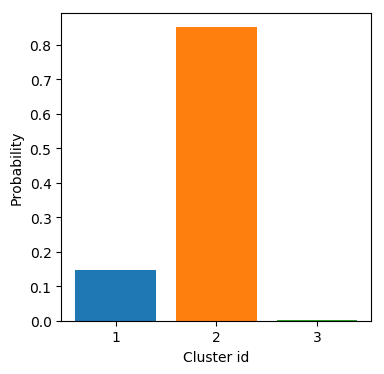
Initial approximation

Expect

Maximize

*Interactive EM demonstration

EM on spatial data

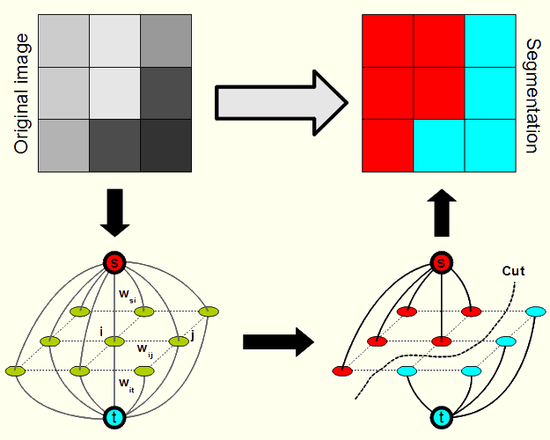
Problem: spatial constraints

EM on spatial data

Solution: Graph Cut Optimization

EM on spatial data

Algorithm v0.02

Initial approximation

Expect

Maximize

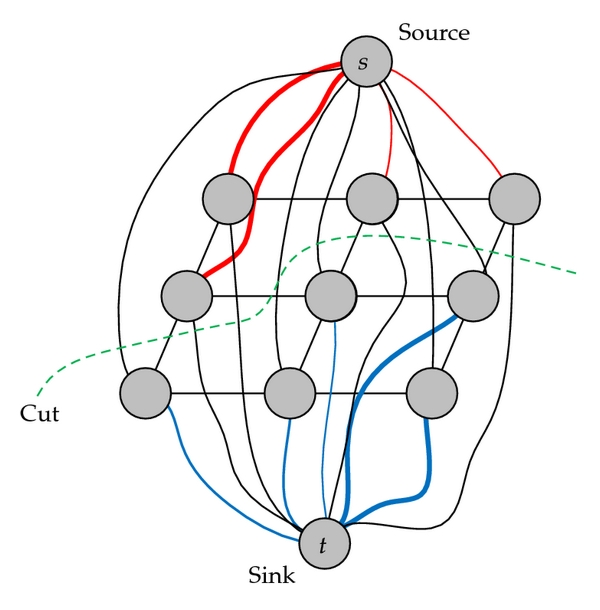
GCO

EM on spatial data

Algorithm v0.02: Results

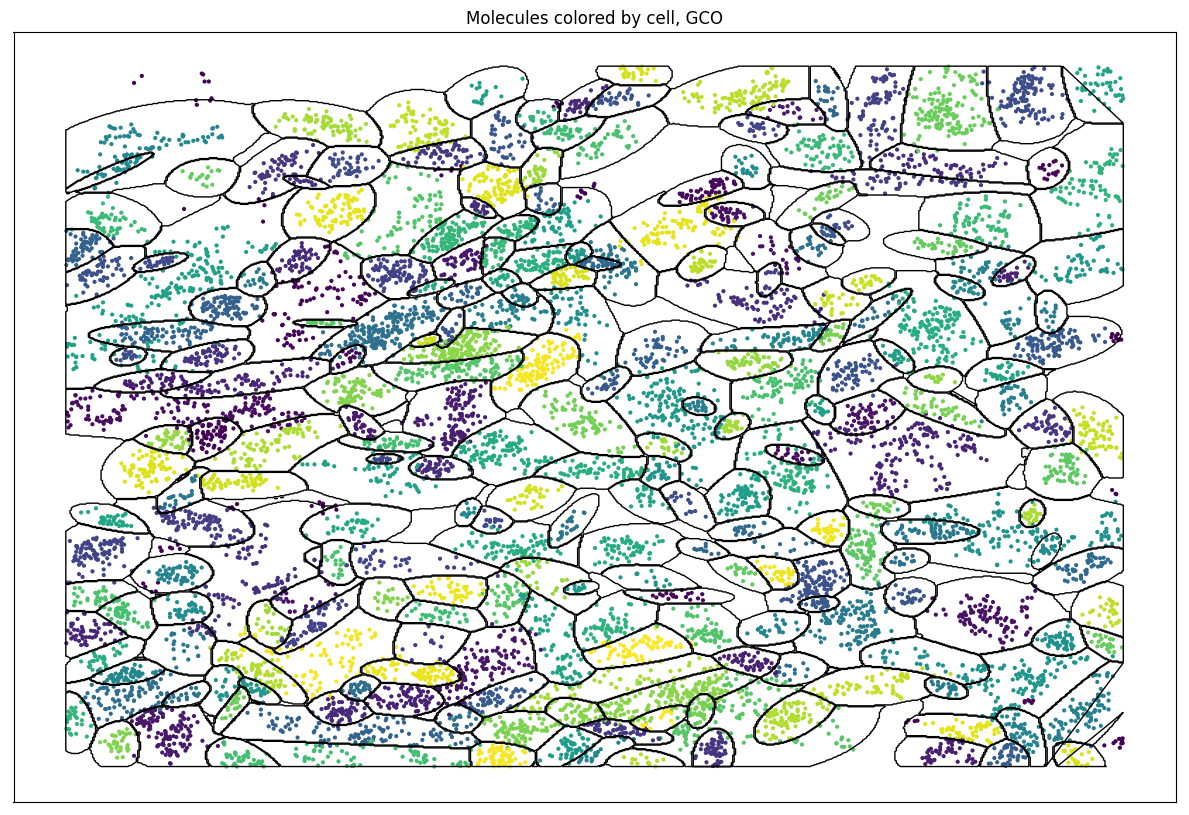
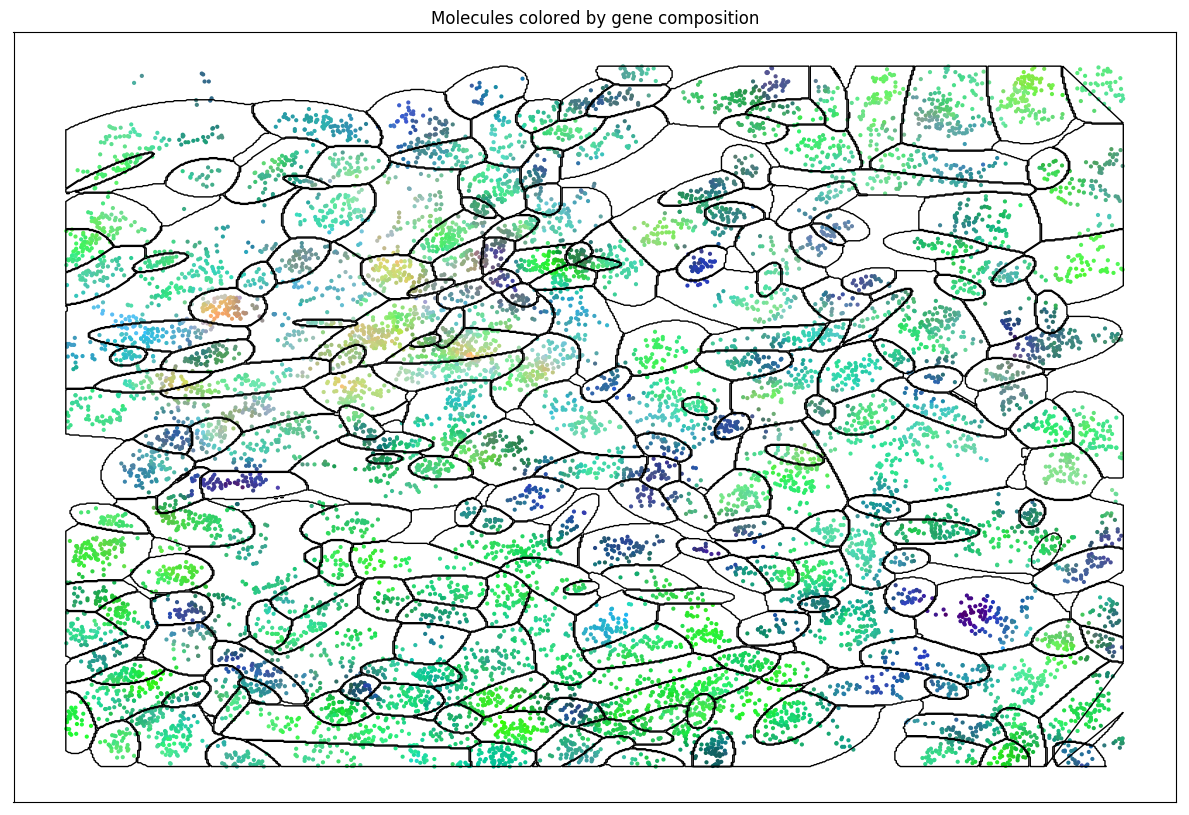
EM on spatial data

Algorithm v0.1: Stochastic EM

Expect

Sample

Maximize

Convergence to global optimum
Doesn't require specification of number of clusters

*Interactive demonstration

EM on spatial data

Algorithm v0.1: Stochastic EM

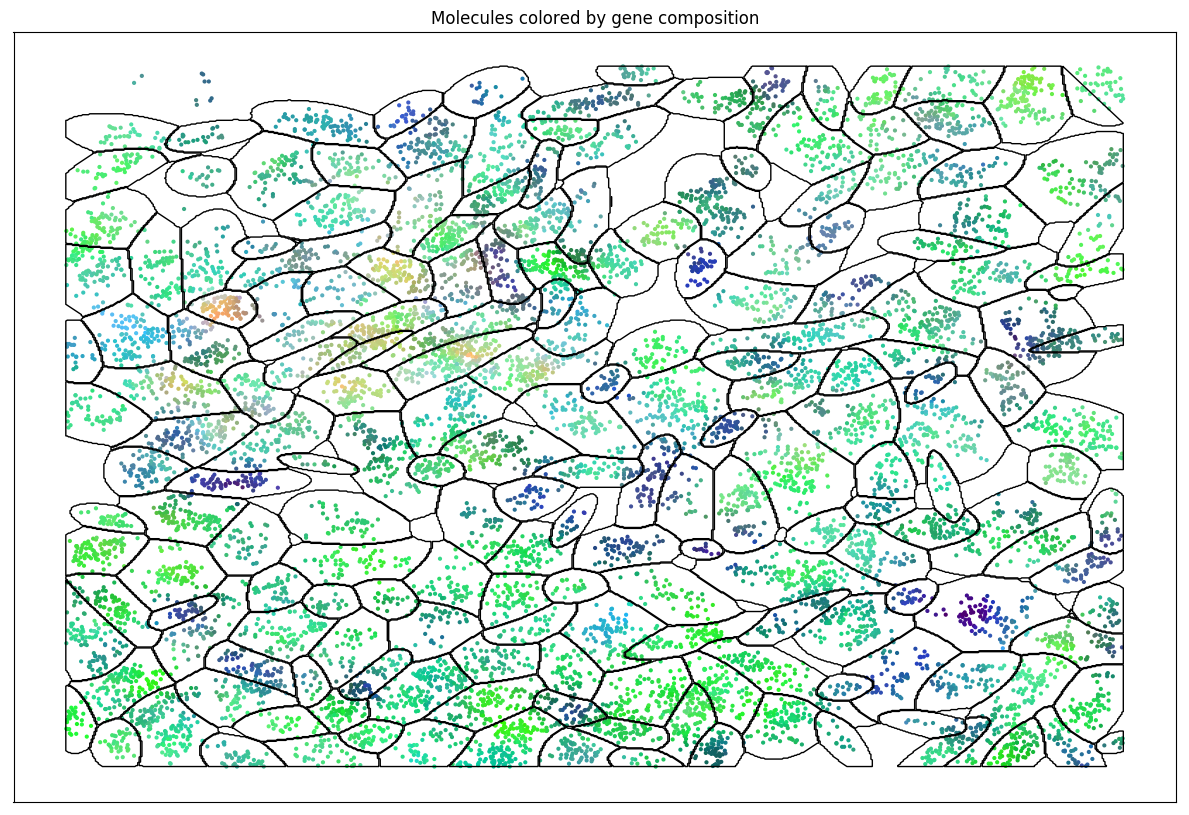
Hierarchical Bayesian Models

Composition prior

Expect

Sample

Maximize