P-value Hell

Viktor Petukhov
viktor.s.petuhov@ya.ru
BRIC, University of Copenhagen
Khodosevich lab
Table of content
- Motivation
- What is p-value?
- What's wrong with p-values?
- How to live without p-values?
- How to live when everyone uses p-values?
Standard workflow
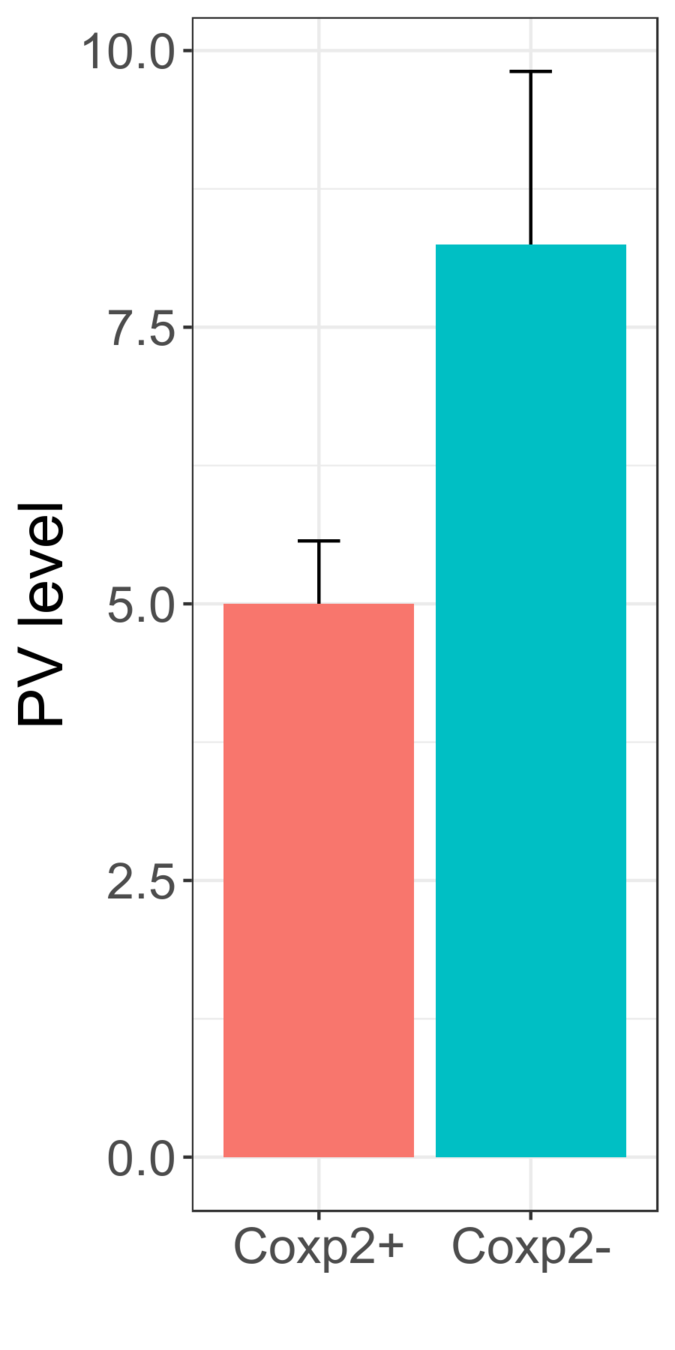
P=0.015
Significant!
The observed decrease in PV levels and synaptic contacts might indicate impaired maturation of PV+ interneurons.
What's that?
How did we understand?
Data
Statistics
P-value
Conclusion
What is p-value?
Comparison of means








Mice on drugs
Average weight: 215g








Mice without drugs
Average weight: 205g
Difference: -10g
Comparison of means
















Hypothesis 0: single group, no difference
Comparison of means
















Hypothesis 0: single group, no difference
Difference: 3g
Comparison of means
















Hypothesis 0: single group, no difference
Difference: -5g
Comparison of means
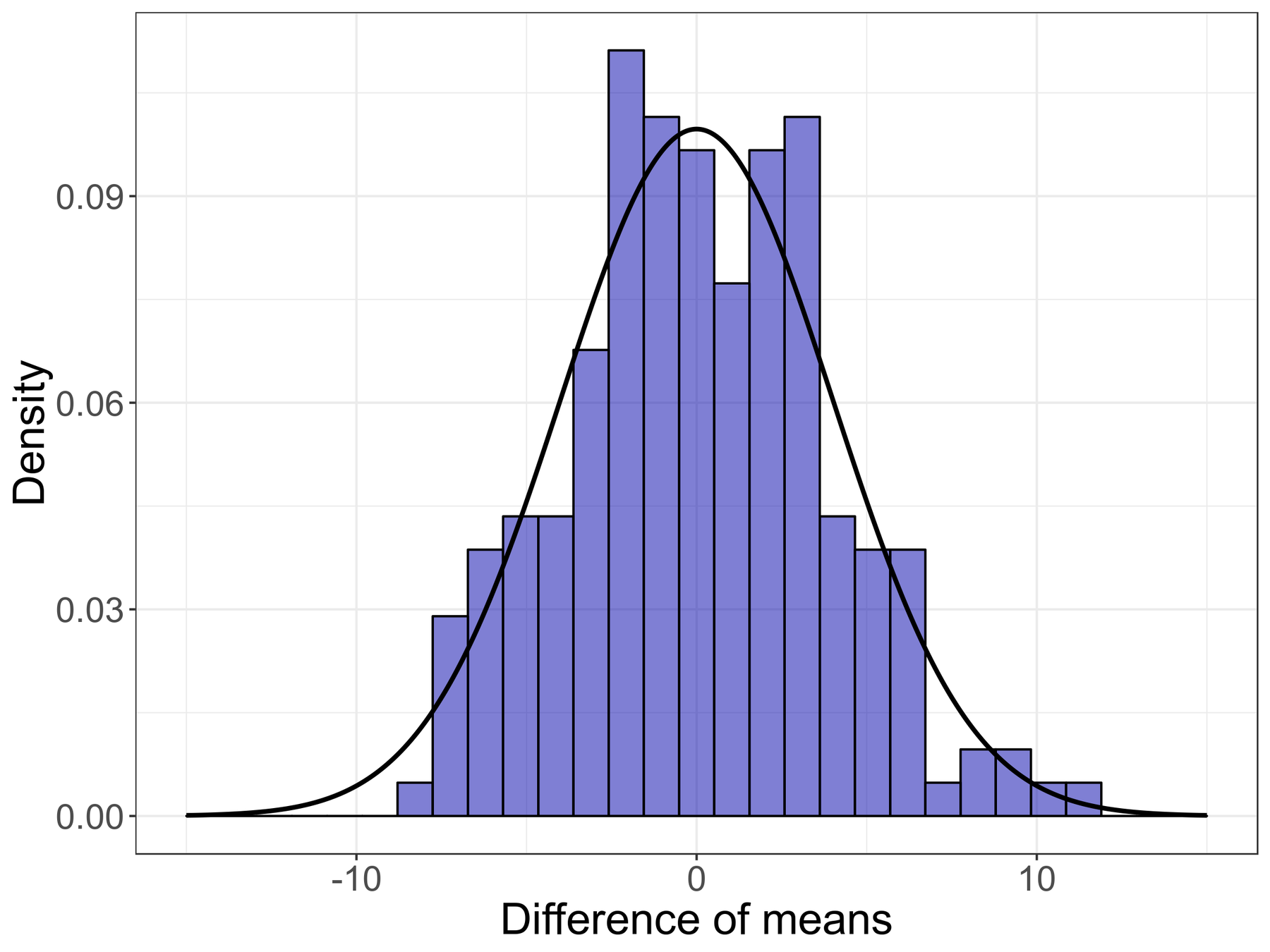
p(difference | H0)
=
False Positive Rate
=
P-value
P-value

What's wrong with it?
P=0.015
Significant!
The observed decrease in PV levels and synaptic contacts might indicate impaired maturation of PV+ interneurons.


Data
Statistics
P-value
Conclusion
What's wrong with
p-values?
Probability to meet a wizard






95%
5%
100%
Actual probability of an error
95%
5%
100%
Difference
Difference
Difference
No
Difference
P-value
Actual probability of an error
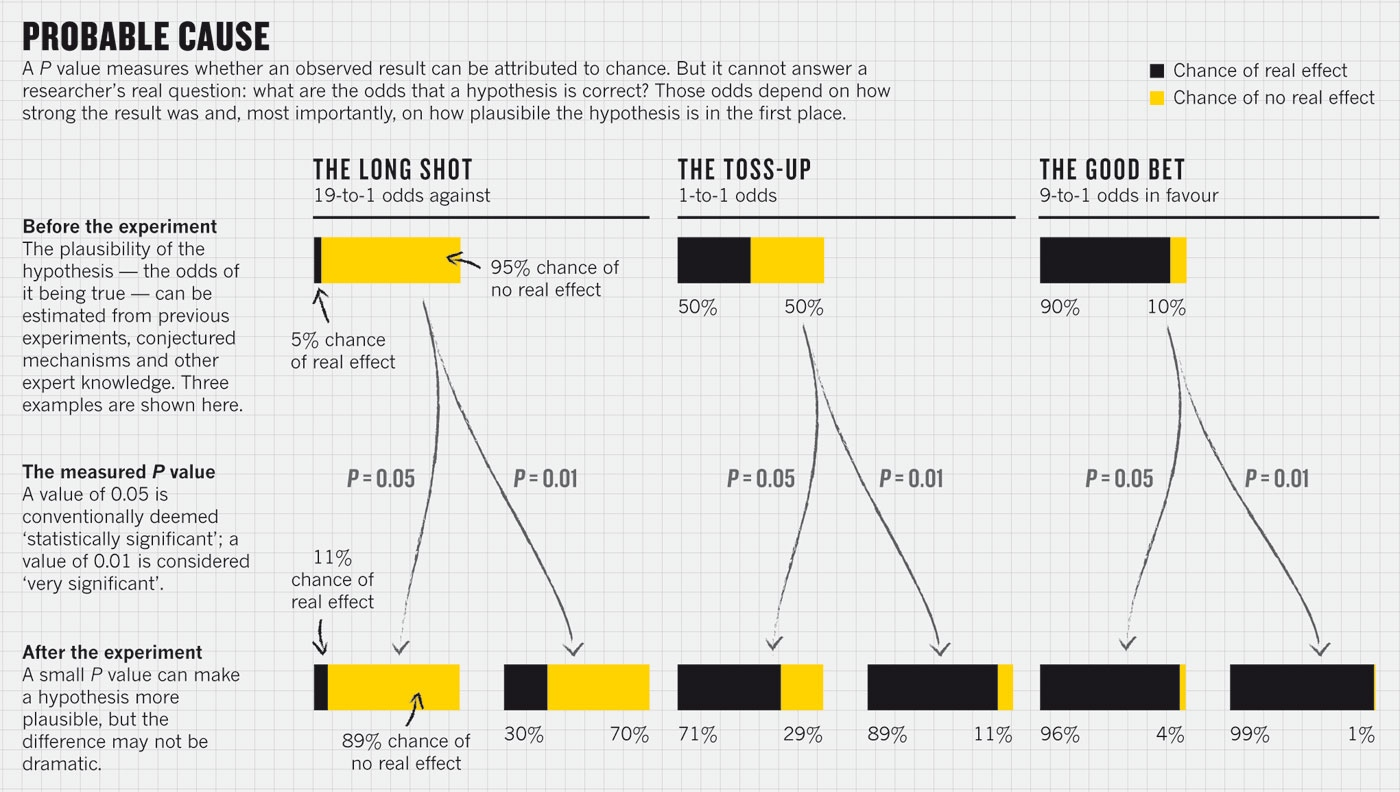
*Regina Nuzzo. Scientific method: Statistical errors. doi:10.1038/506150a
Hypotheses don't represent underlying models
Cells [...] were markedly less bright than [...]. Thus, the MEF2-binding site might set steady-state levels of Cox6a2 expression and E-box fine tunes the specificity.
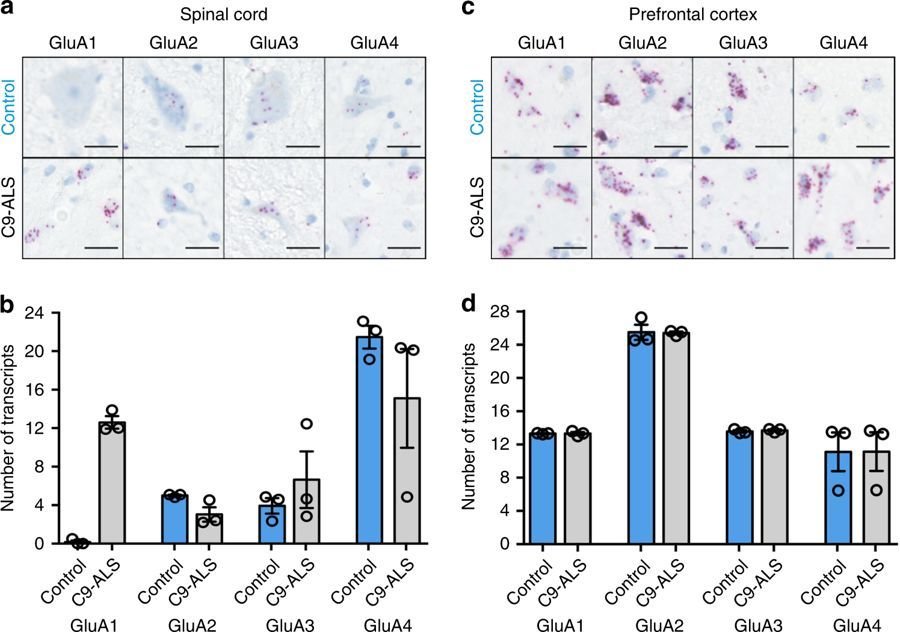
P-value is not a 100% proof of the conclusion
P-value:
0.015
Significant!
The observed decrease in PV levels and synaptic contacts might indicate impaired maturation of PV+ interneurons.
Online daters do better in the marriage...
PNAS, 2013
Study on more than 19,000 people:
those who meet their spouses online are less likely to divorce (p < 0.002) and more likely to have high marital satisfaction (p < 0.001) than those who meet offline
*J. Cacioppo, et. al. Marital satisfaction and break-ups differ across on-line and off-line meeting vensdues. https://doi.org/10.1073/pnas.1222447110
Regina Nuzzo. Scientific method: Statistical errors. doi:10.1038/506150a
Divorce rate:
7.67% vs 5.96%
Happiness:
5.48 vs 5.64

Can we compare p-values?


P-value: 0.02
Previous study:
P-value: 0.001
Your study:

Significant p-value VS Common Sense
Sources:
- Outliers
- Broken test assumptions
- Modification of data, which results in significant difference (p-hacking)
- Bad luck
Summary
- No information about size of effect
- No way to aggregate p-values across several studies
- No way to integrate prior knowledge
- No way to estimate real probability of an error
- Mistakenly considered as a 100% proof
- Hypotheses, which we test, are weakly connected to real models
- Easy to fool yourself
Solution:
Bayesian models
Intro: Bayesian Statistics
“any mathematical statistician would be totally bummed at the informality [of this book], dude.”

John Kruschke - Doing Bayesian Data Analysis A Tutorial with R, JAGS, and Stan
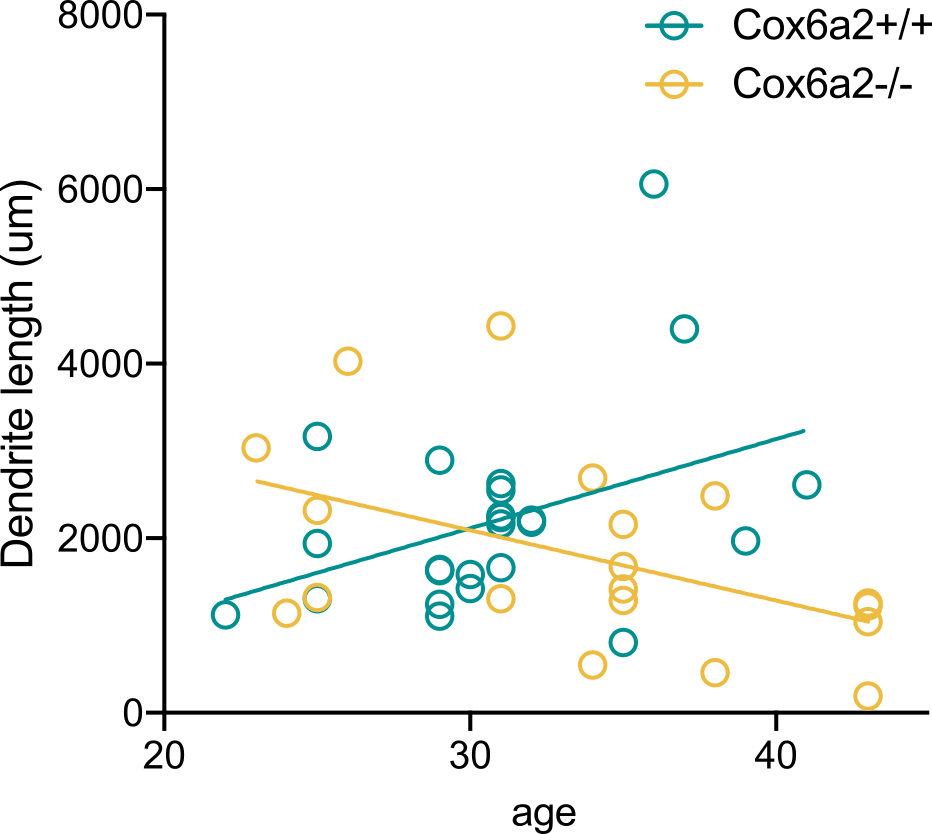
Model vs hypothesis

Hypothesis:
Linear regression has non-zero slope
Model:
Dendrite length ~ S * Age + Noise
Noise ~ Normal(mean=0, std=1)
Prior knowledge:
S ~ Normal(mean=0.2, std=0.1)
Model vs hypothesis

Model 1:
Length ~ S * Age + Noise
Noise ~ Normal(0, 1)
Prior probability: p0=0.1
Model 2:
Length ~ m + Noise
Noise ~ Normal(0, 1)
Prior probability: p0=0.9
Two types of analysis
Evidence
Evidence
Evidence
...
Evidence
Model
Evidence
Evidence
Evidence
...
Evidence
Exploration
_
_
Confirmation
Experiment 1
Experiment 2
Two types of analysis
Evidence
Evidence
Evidence
...
Evidence
Model
Evidence
Evidence
Evidence
...
Evidence
Exploration
_
_
Confirmation
Experiment 1
Experiment 2
Don't care about significance
Don't use p-values
Validation of a model
Bayesian Factor
Popular modifications:
- Akaike Information Criterion
- Bayesian Information Criterion
See "Goodman S.N. - Toward evidence-based medical statistics. 2: The Bayes factor." for more info
Validation of a model
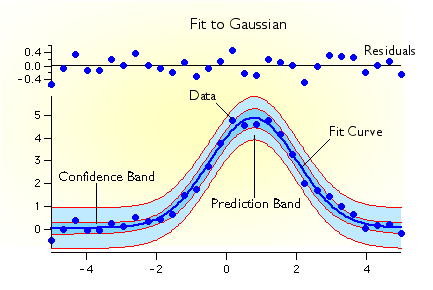
*https://www.wavemetrics.com/products/igorpro/dataanalysis/curvefitting
Residuals and confidence band
Validation of a model
Predictive power

Predictions
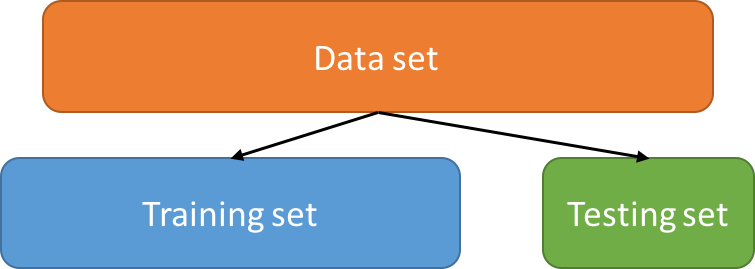
Validation of a model
Train-test split / Cross-Validation
Two types of analysis
| P-values | Bayesian |
|---|---|
| No information about effect size | Effect size is fitted by a model |
| No way to aggregate p-values across several studies | Hierarchical models |
| No way to integrate prior knowledge | Prior probabilities |
| No way to estimate error probability | Prior probabilities |
| Mistakenly considered as a 100% proof | Gives "goodness of fit", but not a binary answer |
| Hypotheses, which we test, are weakly connected to real models | Can use very complex models |
| Easy to fool yourself | More transparent system with priors (but still you can do it) |
How to live in the p-value world
Logo of wrong statistics
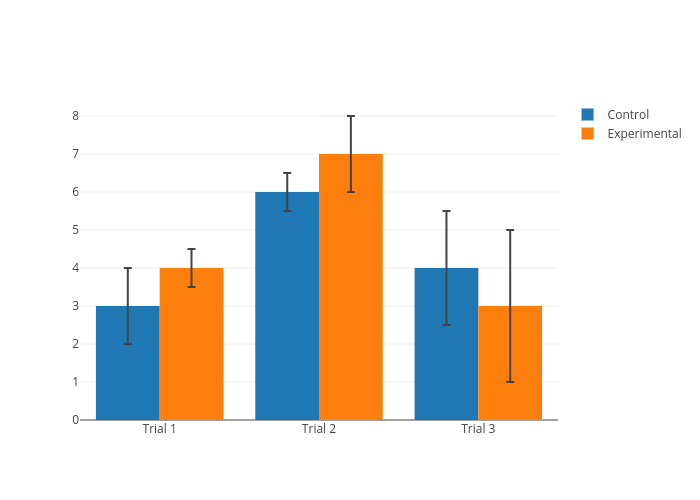
For normal distribution:
- Std show effect size
- SE allows to validate significance of p-values
For non-normal distribution:
- Std means nothing
- SE means nothing
Proper visualization
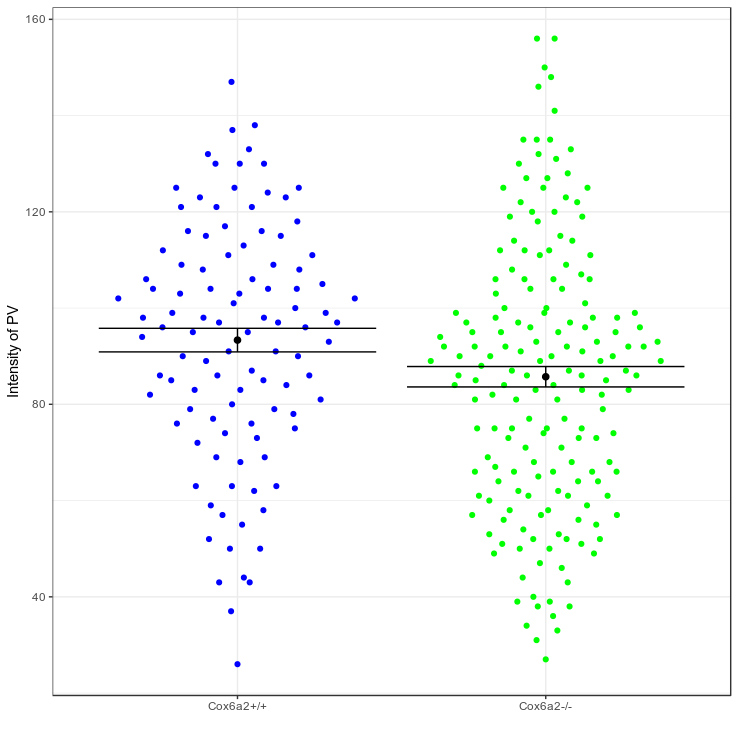
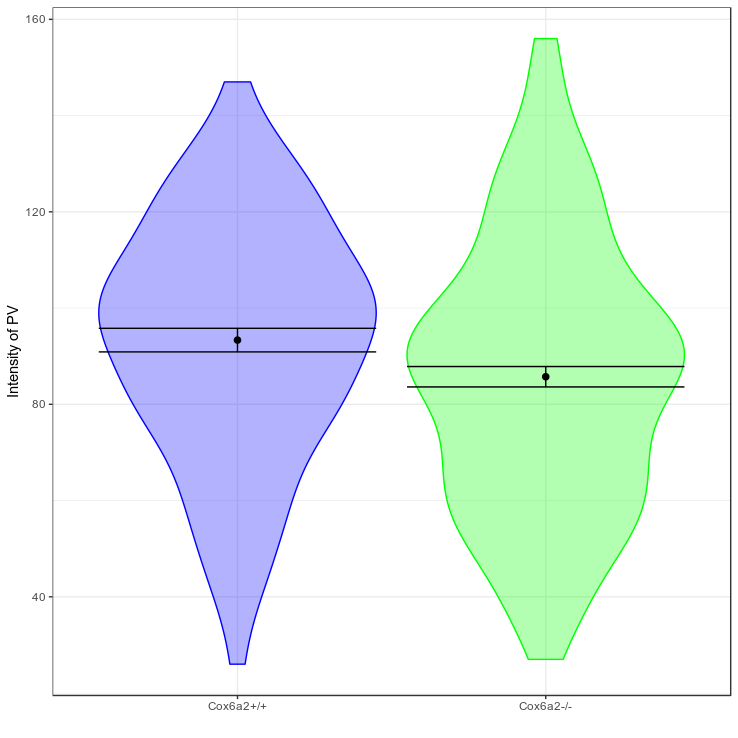
Confidence intervals
Small data
Big data
Multiple comparison
adjustment




Multiple comparison
adjustment
Avoid selective reporting
- Predetermine rule for publishing of the data and results
- Publish this rule
- Publish all data according to this rule
- Publish all manipulations and all measures in the study
Avoid selective reporting
Validation: P-curve

Avoid selective reporting
Validation: P-curve
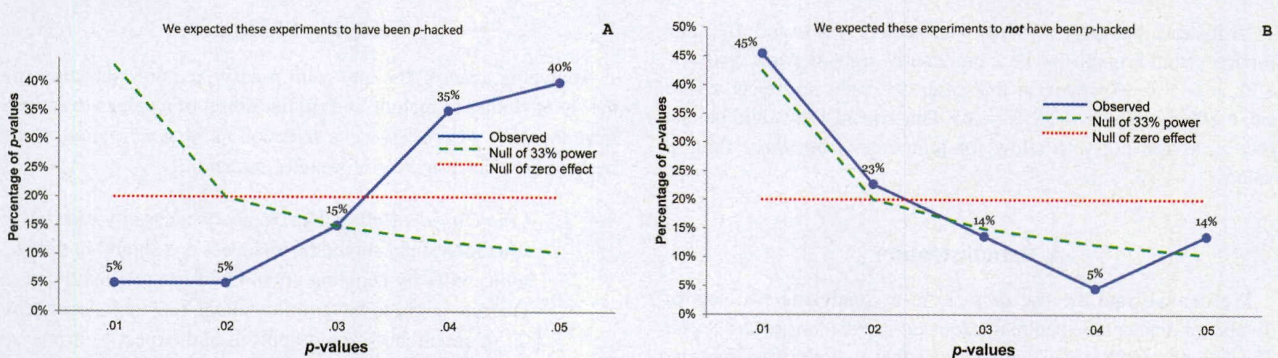
Summary
| Problem | Solution |
|---|---|
| No information about effect size | Better reporting (e.g. swarmplots with confidence intervals) |
| No way to aggregate p-values across several studies | Adjustment for multiple comparisons |
| No way to integrate prior knowledge | - |
| No way to estimate error probability | - |
| Mistakenly considered as a 100% proof | Keep in mind: p-value is just an evidence. Rely on common sense. |
| Hypotheses, which we test, are weakly connected to real models | Use better hypotheses, learn underlying assumptions |
| Easy to fool yourself | Predetermine rule for publishing and follow it |
References
- Nuzzo, R. (2014), “Scientific Method: Statistical Errors,” Nature, 506, 150–152. doi:10.1038/506150a
- Goodman, S. N. (1999). Toward evidence-based medical statistics: I. The p value fallacy. Annals of Internal Medicine, 130, 995–1004. doi:130(12):995-1004
- Greenland, S., Senn, S.J., Rothman, K.J., Carlin, J.B., Poole, C., Goodman, S.N. and Altman, D.G.: “Statistical Tests, P-values, Confidence Intervals, and Power: A Guide to Misinterpretations.
- Simonsohn, U., Nelson, L. D., & Simmons, J. P. (2014). P-curve: A key to the file-drawer. Journal of Experimental Psychology: General, 143(2), 534–547. doi:10.1037/a0033242
- Ronald L. Wasserstein & Nicole A. Lazar (2016) The ASA's Statement on p-Values: Context, Process, and Purpose, The American Statistician, 70:2, 129-133, DOI: 10.1080/00031305.2016.1154108
Further Reading
- W. Beatty - Decision Support Using Nonparametric Statistics. Statistics for very beginners without single formulas.
-
John Kruschke - Doing Bayesian Data Analysis A Tutorial with R, JAGS, and Stan. Extremely informal and well-written book on Bayesian Statistics.
- Andrew Gelman, et al. - Bayesian Data Analysis. The Bible of Bayesian Statistics. All you ever need in real life is probably in this book.
Thank you!
Viktor Petukhov
University of Copenhagen
Khodosevich lab
viktor.s.petuhov@ya.ru