Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN

CVPR 2018

Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, Yanbo Gao

https://arxiv.org/abs/1803.04831

Outline

RNNs
Mathematical Notation
Independently RNN(Ind RNN)
Conclusion
Experiments
Question

RNNs

Vanilla RNN
- Pros:
  - Share parameters across time steps.
  - Computational graph is deeper than CNN.
- Cons:
  - Gradients tend to vanish.

http://colah.github.io/posts/2015-08-Understanding-LSTMs/

RNNs

LSTM
- Cons:
  - Can process longer sequence than Vanilla RNN.
- Pros:
  - Need huge computational resources.
  - Can't be stacked very deep.

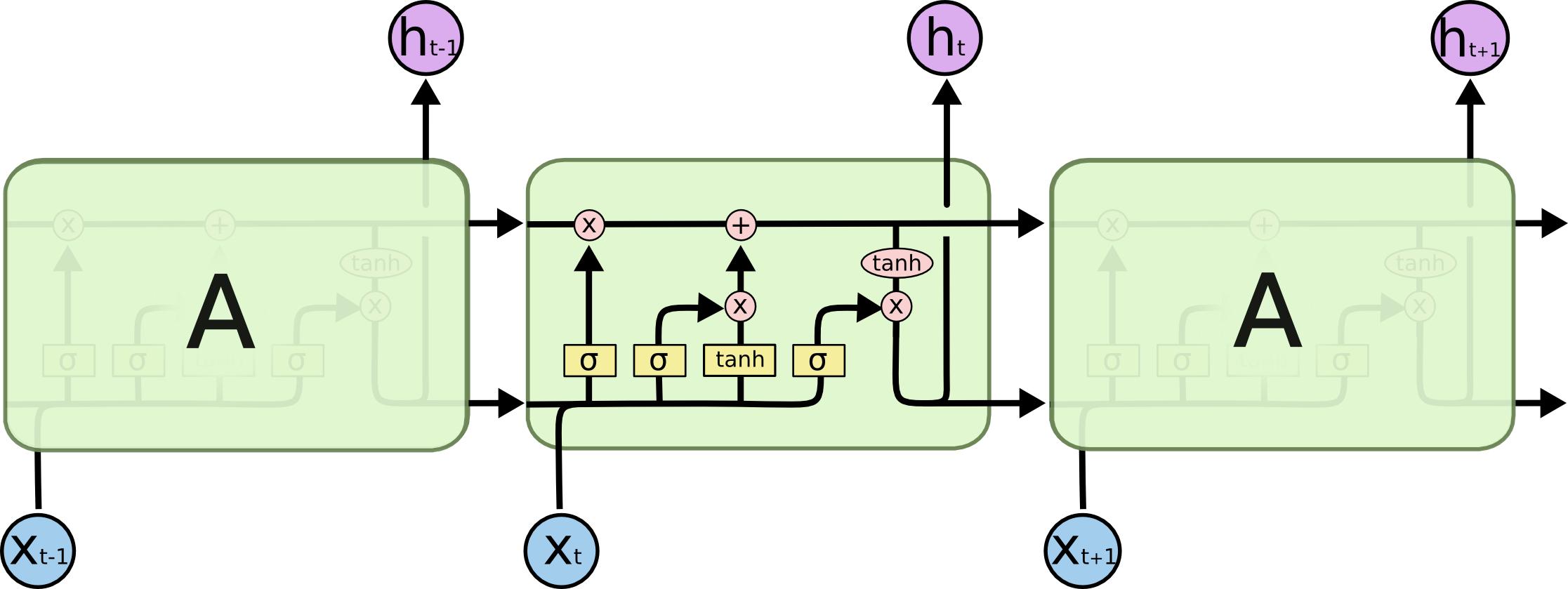
http://colah.github.io/posts/2015-08-Understanding-LSTMs/

Mathematical Notation

Scalar: normal symbol, e.g., $\mathrm{a}, \mathrm{c}$
Vector: italic symbol, e.g., $h, x$
Matrix: bold symbol, e.g., $\mathbf W, \mathbf U$
Element wise multiplication operator: $\odot $
Activation function: $\sigma(x), \phi(x)$

Independently RNN

$$\tag{1} h_t=\sigma(\textbf Wx_t+u\odot h_{t-1}+b)$$

$h_t$ is the hidden state at time $\mathrm t$, $x_t$ is the input at time $\mathrm t$.

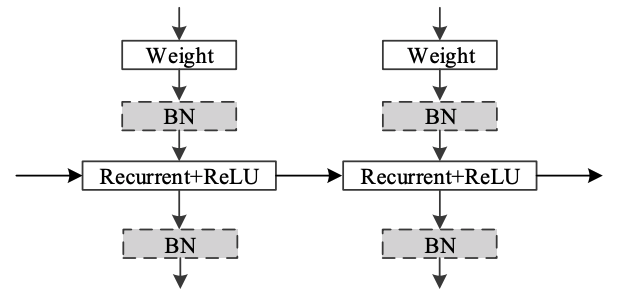
Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

BPTT for IndRNN

$$\tag{1} h_t=\sigma(\textbf Wx_t+u\odot h_{t-1}+b)$$

Consider single neuron in equation $(1)$

$$\tag{2}\mathrm h_{n,t}=\sigma(w_nx_t+\mathrm u_n\mathrm h_{n,t-1}+\mathrm b_n)$$

$\mathrm h_{n,t}$ and $\mathrm u_n$ is the $n-th$ neuron in $h_t$ and $u$.

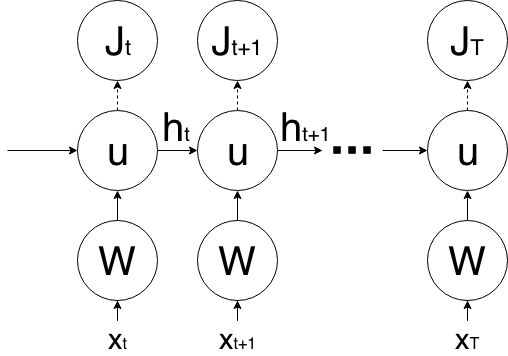
BPTT for IndRNN

$$\tag{2}\mathrm h_{n,t}=\sigma(w_nx_t+\mathrm u_n\mathrm h_{n,t-1}+\mathrm b_n)$$

$$\gdef\rm#1{\mathrm{#1}}\def\head{\frac{\partial \rm{J}_T}{\partial \rm{h}_{n,T}}}\begin{aligned}\frac{\partial \rm{J}_T}{\partial \rm{h}_{n, t}}&=\head\frac{\partial \rm{h}_{n,T}}{\partial \rm{h}_{n, t}}=\head\prod_{k=t}^{T-1}\frac{\partial \rm{h}_{n, k+1}}{\partial \rm{h}_{n, k}}\\&=\head\prod_{k=t}^{T-1}\sigma'_{n, k+1}\rm{u}_n\\&=\tag{3}\head \rm{u}_n^{T-t}\prod_{k=t}^{T-1}\underbrace{\sigma'_{n, k+1}}_{\text{activation}}\end{aligned}$$

$\mathrm J_T$ is the objective at time step $\mathrm T$.

BPTT for IndRNN

From equation $(3)$

$$\gdef\rm#1{\mathrm{#1}}\def\head{\frac{\partial \rm{J}_T}{\partial \rm{h}_{n,T}}}\frac{\partial \rm{J}_T}{\partial \rm{h}_{n, t}}=\head \underbrace{\rm{u}_n^{T-t}\prod_{k=t}^{T-1}\sigma'_{n, k+1}}_{\text{only consider this term}}$$

Keep gradient in specific range $[\epsilon, \gamma]$ to vaoid gradient vanishing and exploding

$$\def\act{\prod_{k=t}^{T-1}\sigma'_{n, k+1}}\gdef\rm#1{\mathrm{#1}}\\\tag{4}\epsilon\le\rm{u}_n^{T-t}\act\le\gamma\\\ \sqrt[T-t]{\frac{\epsilon}{\act}}\le\rm{u}_n\le\sqrt[T-t]{\frac{\gamma}{\act}}$$

BPTT for IndRNN

From equation $(4)$, choose ReLU as activation

$$\def\act{\prod_{k=t}^{T-1}\sigma'_{n, k+1}}\gdef\rm#1{\mathrm{#1}}\\\tag{5}\sqrt[T-t]{\epsilon}\le\rm{u}_n\le\sqrt[T-t]{\gamma}$$

If necessary, relax lower bound to $0$ to forget previous state and only consider current input $x_t$

$$\def\act{\prod_{k=t}^{T-1}\sigma'_{n, k+1}}\gdef\rm#1{\mathrm{#1}}\\\tag{6}0\le\rm{u}_n\le\sqrt[T-t]{\gamma}$$

Multiple-Layer IndRNN

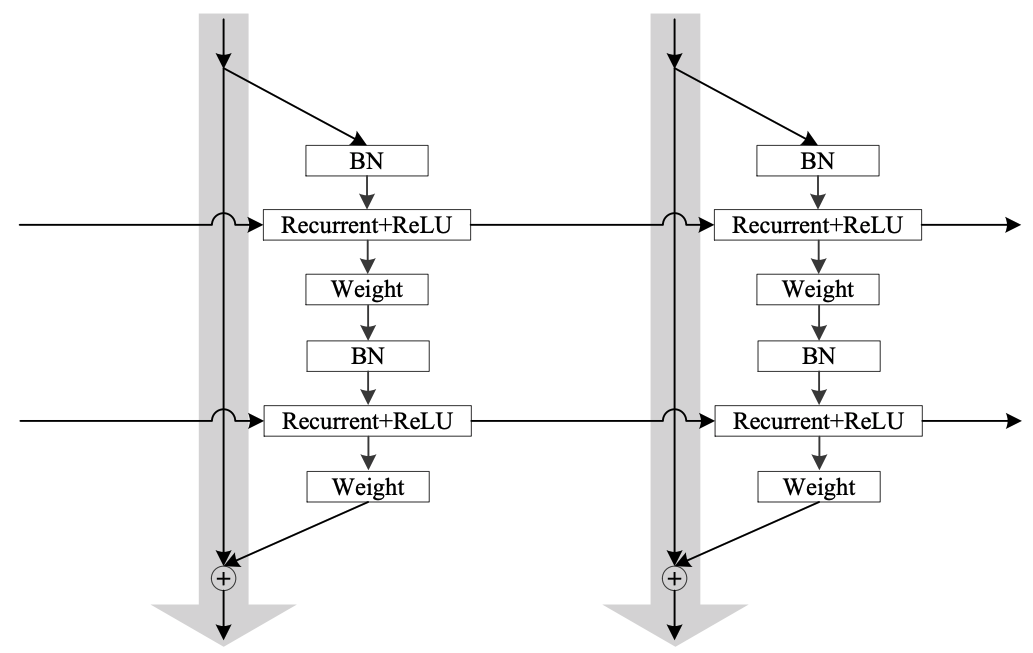
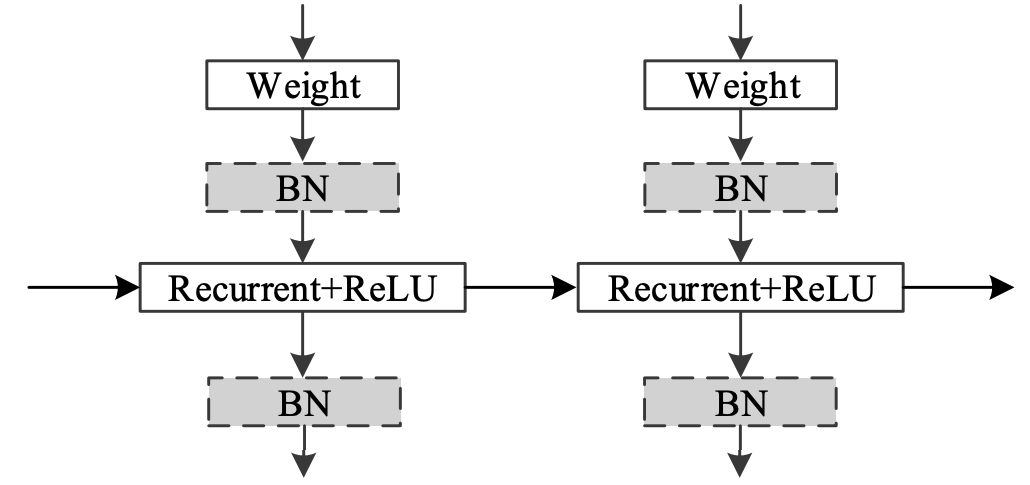
Single Layer IndRNN

Residual IndRNN

Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

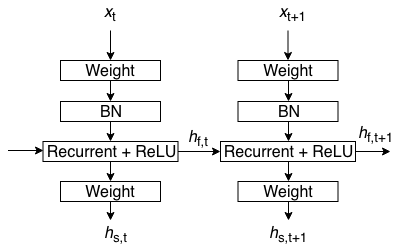
IndRNN vs Vanilla RNN

rewrite equation $(1)$ and add second fully connected layer $h_{s, t}$

$$\begin{aligned}\tag{7}h_{f, t}&=\mathbf W_fx_t+diag(u)h_{f, t-1}\\h_{s, t}&=\mathbf W_sh_{f, t}\end{aligned}$$

solve equations $(7)$, we have

$$h_{s, t}=\mathbf Wx_t+\mathbf Dh_{s, t-1}$$

$\mathbf D$ is a diagonalizable matrix. Compare to Vanilla RNN

$$h_{s, t}=\mathbf Wx_t+\mathbf Uh_{s, t-1}$$

$\mathbf U \in R^{2}$

Architecture	Space Complexity	Time Complexity
Vanilla RNN
1-layer IndRNN
2-layer IndRNN

$M\times N+N\times N$

IndRNN vs Vanilla RNN

$M\times N+N$

$M\times N+N\times N + 2\times N$

$N\times N\times T$

$N\times T$

$2\times N\times T$

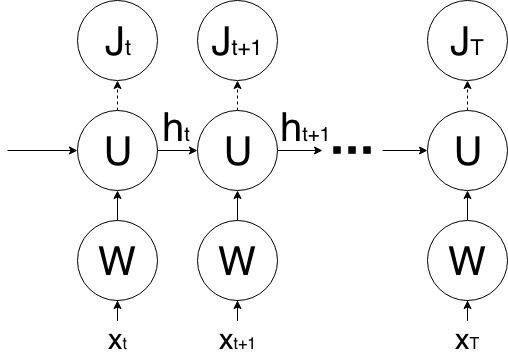
IndRNN

Vanilla RNN

Experiments

Adding Problem
Sequential MNIST Classification
Language Modeling
Skeleton based Action Recognition

Adding Problem

Input sequences:

$$\begin{aligned}x_1&,& \cdots &,& x_{n1}&,&\cdots &,& x_{n2}&,& \cdots &,& x_T\\0&,& \cdots&,& 1&,& \cdots&,& 1&,& \cdots&,& 0\\\end{aligned}$$

Regression output:

$$x_{n1}+x_{n2}$$

Adding Problem

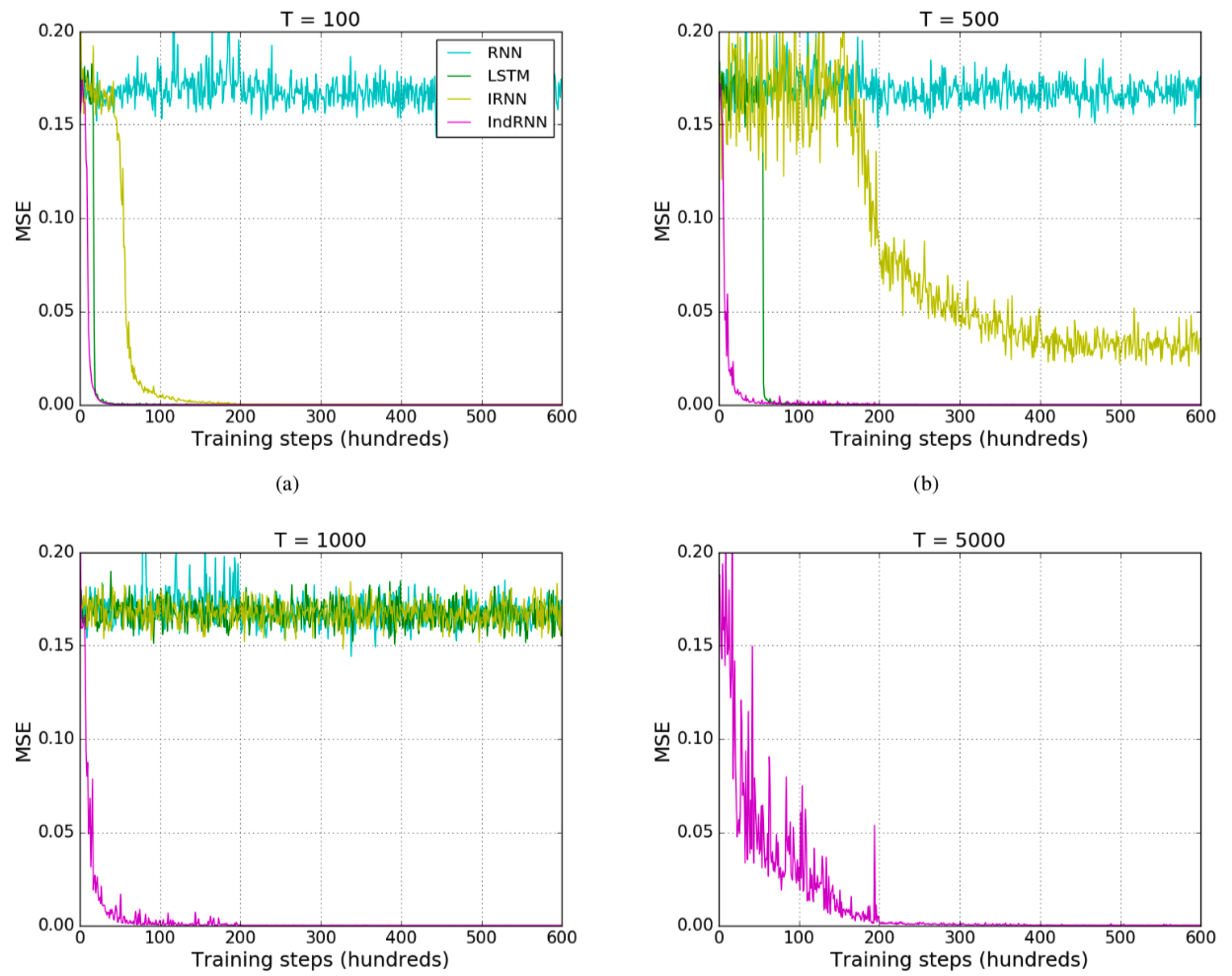
Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

Adding Problem

Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

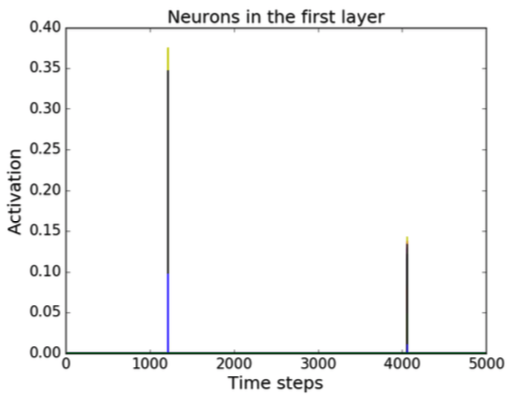
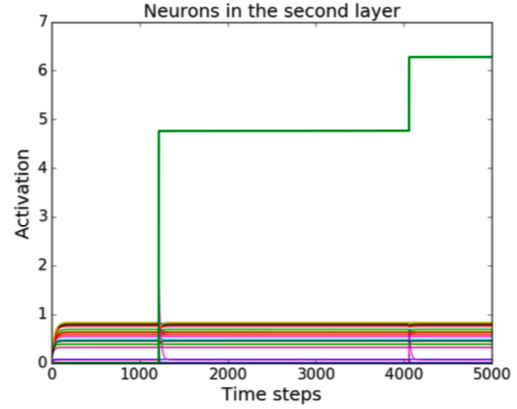
Sequential MNIST Classification

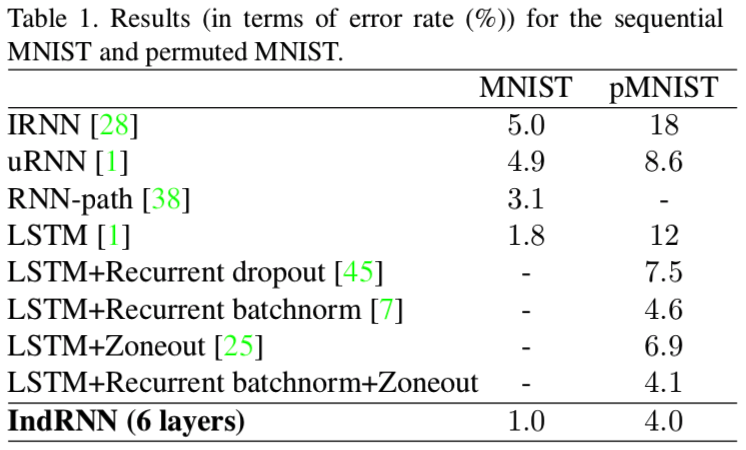
Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

Language Modeling

Dataset: word-level Penn TreeBank (PTB-c)
Metric: $perplexity(S)=\sqrt[m]{\prod_{i=1}^m\frac{1}{P(w_i|w_1,w_2,\cdots,w_{i-1})}}$

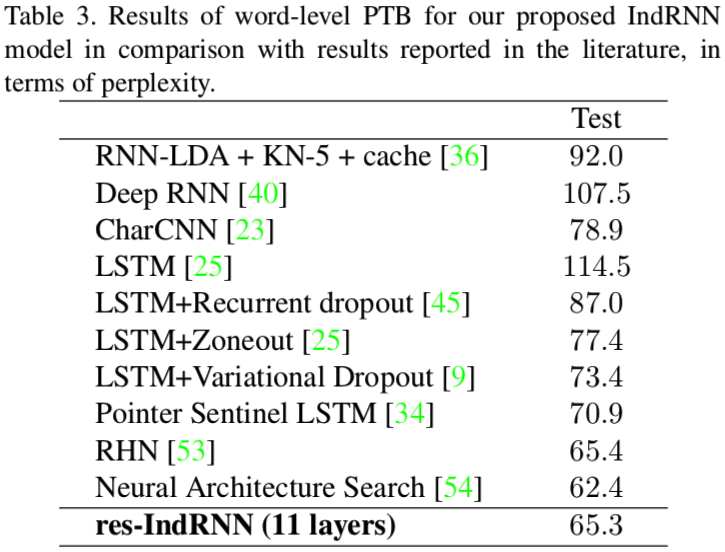
Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

Language Modeling

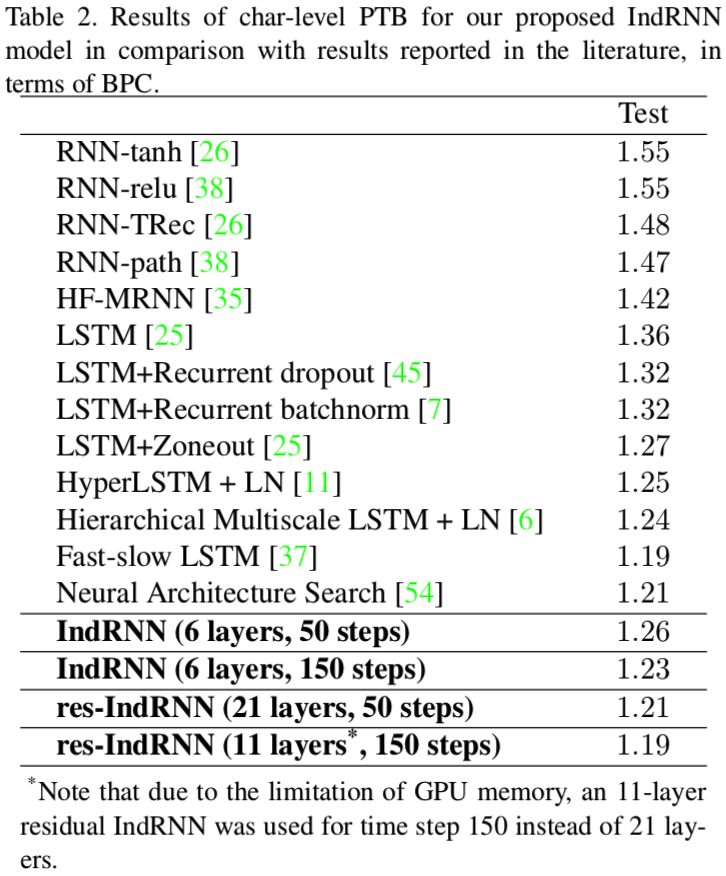
Dataset: character-level Penn TreeBank (PTB-c)
Metric: bits per character (BPC)

Shuai Li, Wanqing Li, Chris Cook, Ce Zhu, and Yanbo Gao. "Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN." CVPR 2018.

Skeleton based Action Recognition

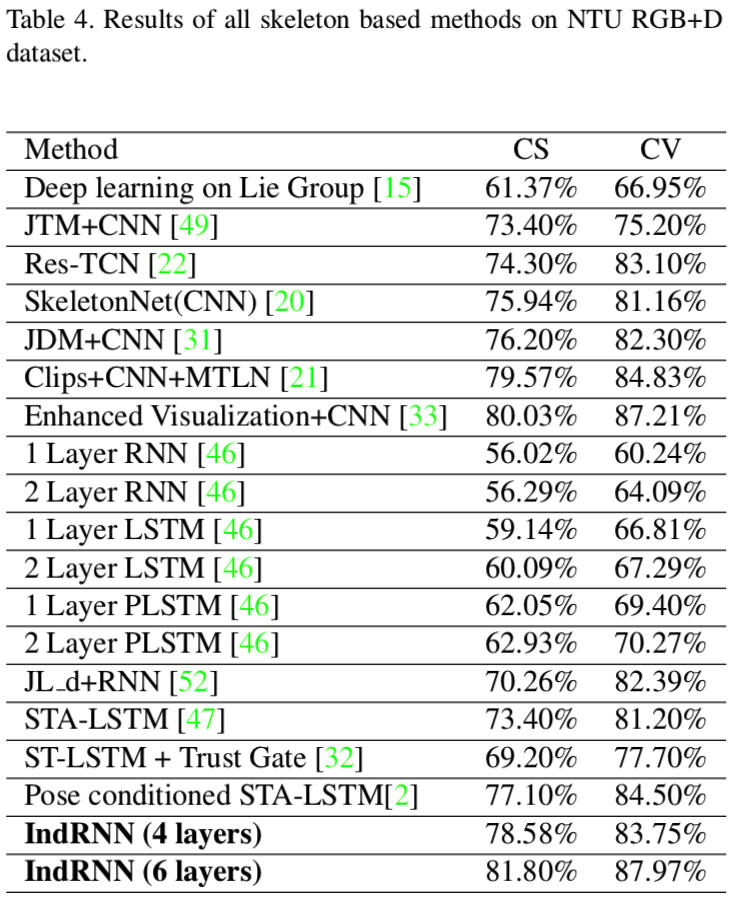
Dataset: NTU RGB-D dataset
Metric: accuracy

Independently RNNs

IndRNN already be implemented in TensorFlow.

Note that TF implementation does not include weight clipping.

Popular implementation: github

import tensorflow as tf

x = ...    # inputs

cell = tf.contrib.rnn.IndRNNCell(num_hidden=128, activation=tf.nn.relu)
hidd = tf.contrib.rnn.static_rnn(cell, x)

Independently RNNs

tf.contrib.rnn.IndyGRUCell, source

$$r_j = \sigma\left([\mathbf W_r\mathbf x]_j +[\mathbf u_r\circ \mathbf h_{(t-1)}]_j\right)\\z_j = \sigma\left([\mathbf W_z\mathbf x]_j +[\mathbf u_z\circ \mathbf h_{(t-1)}]_j\right)\\\tilde{h}^{(t)}_j = \phi\left([\mathbf W \mathbf x]_j +[\mathbf u \circ \mathbf r \circ \mathbf h_{(t-1)}]_j\right)$$

tf.contrib.rnn.IndyLSTMCell, source

$$\begin{aligned}f_t &= \sigma_g\left(W_f x_t + u_f \circ h_{t-1} + b_f\right)\\i_t &= \sigma_g\left(W_i x_t + u_i \circ h_{t-1} + b_i\right)\\o_t &= \sigma_g\left(W_o x_t + u_o \circ h_{t-1} + b_o\right)\\c_t &= f_t \circ c_{t-1} +i_t \circ \sigma_c\left(W_c x_t + u_c \circ h_{t-1} + b_c\right)\end{aligned}$$

Conclusion

IndRNN try to address following issues
- Avoid gradient vanishing and exploding.
- Process longer sequences.
- Work with ReLU.
- Can be stacked deeper.

Question

1. Use Frame-wise or Sequence-wise batch normalization ?

2. Compare weight clipping and gradient clipping, what is the advantage of weight clipping?

RNNs-Appendix

Vanilla RNN
- Representation:$$h_t=\sigma(\textbf Wx_t+\textbf Uh_{t-1})$$
- BPTT: $$\frac{\partial \mathrm{J}_T}{\partial h_t}=\frac{\partial \mathrm{J}_T}{\partial h_T}\prod_{k=t}^{T-1}diag(\sigma'(h_{k+1}))\mathbf U^T$$
LSTM
- Representation:$$\begin{aligned}\begin{pmatrix}i_t \\ f_t \\ o_t \\ g_t\end{pmatrix}&=\begin{pmatrix}\sigma \\ \sigma \\ \sigma \\ \phi \end{pmatrix} (\textbf Wx_t+\textbf Uh_{t-1})\\s_t&=g_t\odot i_t+s_{t-1}\odot f_t\\h_t&=\phi (s_t)\odot o_t\end{aligned}$$
- BPTT: $???$