最佳投票方案(騙人的
2014/11/16 雞蛋糕哲學講座

洪偉
沃草專案經理
偉恩與咖啡格主
團體為什麼要進行決策?如何進行決策?
以下的決策方式哪裡不好?
- 在吵架的時候,最後一個哭的決定
- 大家吵累了以後,還有力氣講話的決定
- 趁麻煩鬼不在的時候偷偷決定
- 打筆戰的時候最後回文的就贏了
團體決策
- 實然上:團體中的個人被設定,有權利參與這個決策
- 應然上:團體決策應該要能代表團體的意志
授權處理
平等參與
所有人的意見都應該在決策時被同等重視
or
共識決
consensus
共識決的好處
- 合作、協作
- 參與
- 充份討論
- ......
發生異議怎麼處理?
- 保留,下次換種提法試試看
- 「有人強烈反對嗎?」
共識決如何失敗?
- 共識決的可能性預設了「可說服性」
- 倔強的人(們)
- 團體人數太多
- 立法院
- 我爸
必須以其他更有效的決定性機制來做決策
投票
如何公平地決定
「要用什麼比賽來公平地決定?」
機制的決定如何決定?
- 要能夠說服大家:機制是公平的
什麼叫作「公平」?
多數決是一個比踢罐子更好的民主決策方式
-
為什麼?
-
因為它更合理
什麼叫作「不合理的機制」?
- 在機制上納入無關的事(班長的姓名、身高、體能)
- 違反「平等參與」原則
- 可能出現不可接受的成果
- 有人永遠不可能獲勝
不合理的投票
可能成為多數暴力
- 氣候變遷會議 COP
- 投票決定他人的居住權
- 政府有權利這麼做嗎?
有哪些投票法?
-
多數決規則
-
方法A
-
方法B
-
方法C
警告
接下來的討論有大量數字分析
在這裡有的兩個假設
-
所有投票者都是誠實的
-
偏好是完全的、線性的
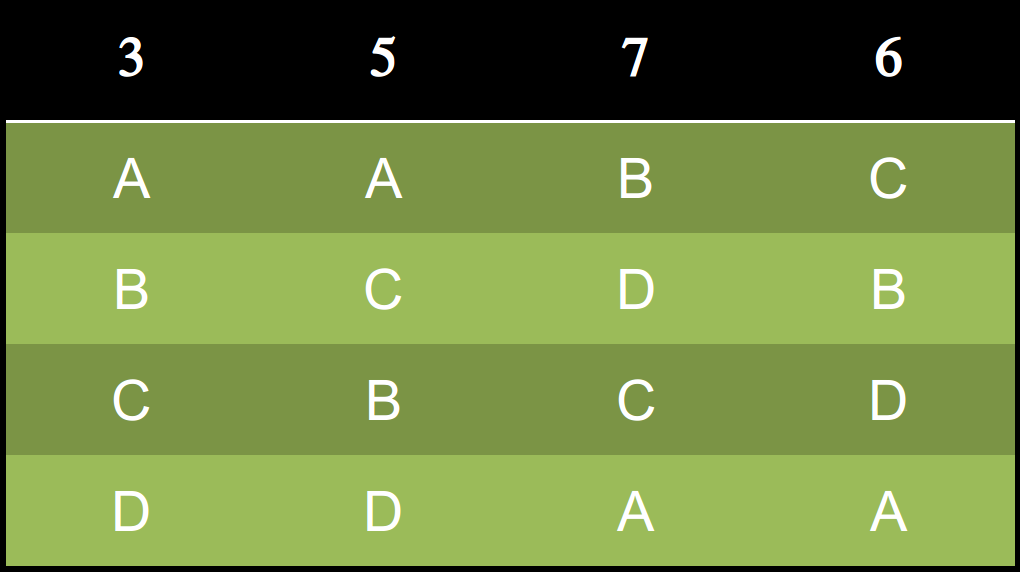
3個人
偏好:A>B>C>D
有3個人覺得他喜歡A勝過B、B勝過C、C勝過D
多數決規則

A勝出
孔多賽規則
PK法

A贏B 8人,B贏A 13人
A贏C 8人,C贏A 13人
A贏D 8人,D贏A 13人
......

我們把這裡的 C 叫作「孔多賽溫拿」
讓我們來算算誰是 PK 王(兩分鐘)
C
伯達計數法

伯達計數法計算的是:「誰贏過最多人?」
(兩分鐘)

BS(A) = 3 × 8 + 2 × 0 + 1 × 0 + 0 × 13 = 24
BS(B) = 3 × 7 + 2 × 9 + 1 × 5 + 0 × 0 = 44
BS(C) = 3 × 6 + 2 × 5 + 1 × 10 + 0 × 0 = 38
BS(D) = 3 × 0 + 2 × 7 + 1 × 6 + 0 × 8 = 20
逐步淘汰法

第一輪
D以0票淘汰
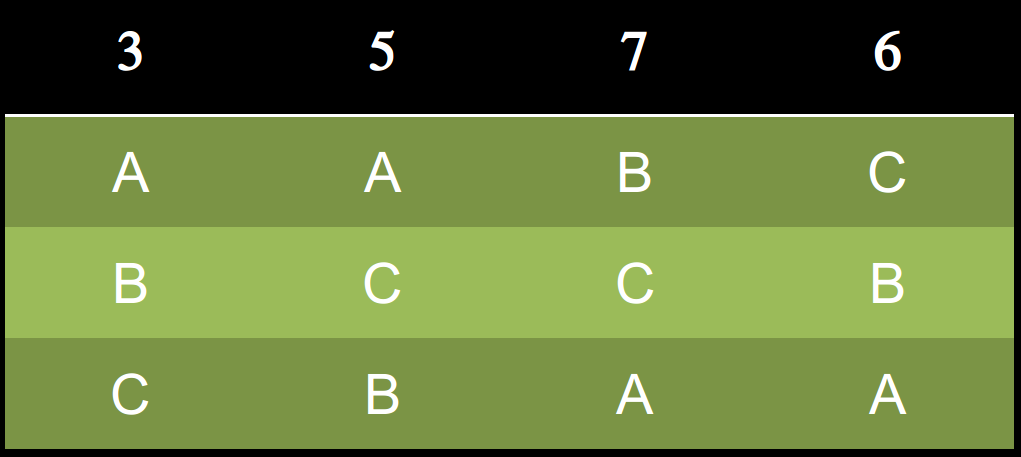
第二輪
C以6票淘汰
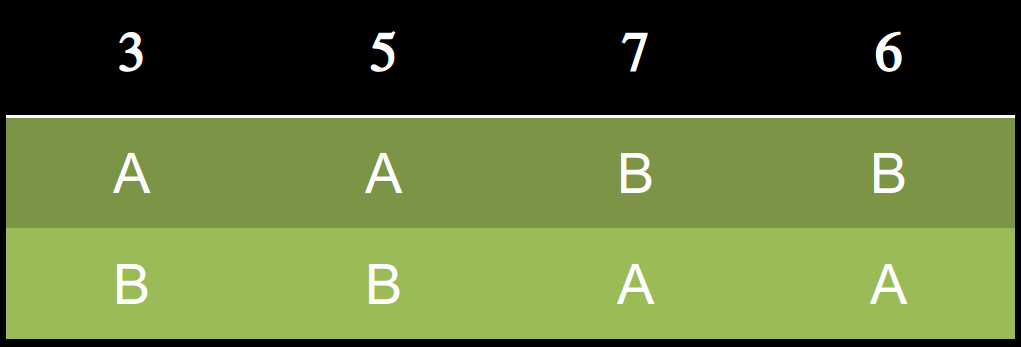
B 勝出
你喜歡哪個投票法?
-
多數決規則
-
逐步淘汰法
-
孔多賽規則
-
伯達計數法
一個直覺
-
孔多賽溫拿不能是魯蛇
有其他辦法能選舉出孔多賽溫拿嗎?
簡單多數決逐步淘汰法- 伯達計數法
伯達計數法的可能性
-
原先我們的計數方式是:你贏過 k 人,就拿到 k 分
-
如果我們在考慮妥當候選人和投票者人數後,將計數的方式調整,讓你在贏過不同人時能得到不同的分數,有沒有可能複製出孔多賽的效果?
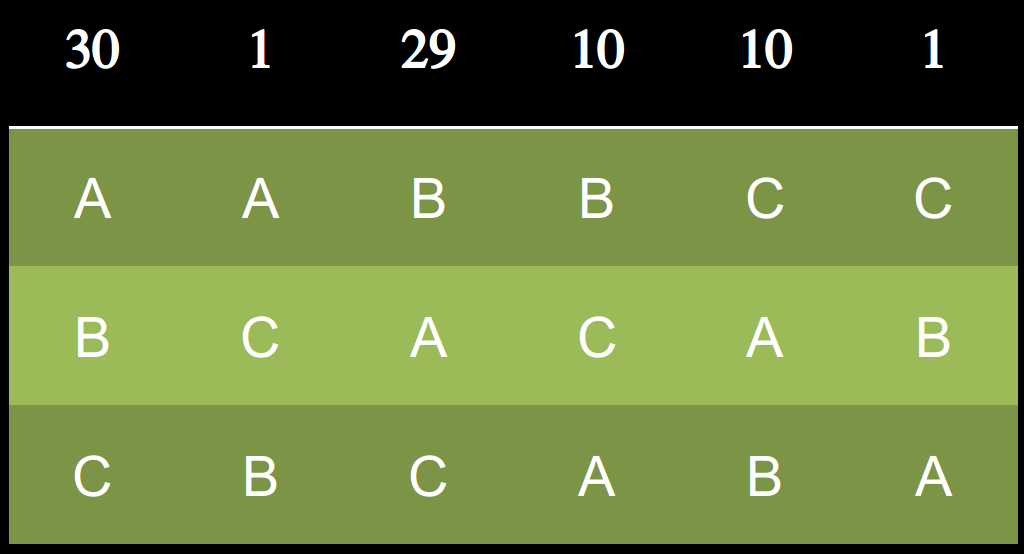
孔多賽溫拿是 A

BS(A) = 2 × 31 + 1 × 39 + 0 × 11 = 101
BS(B) = 2 × 39 + 1 × 31 + 0 × 11 = 109
BS(C) = 2 × 11 + 1 × 11 + 0 × 59 = 33

BS(A) = 2 × 31 + t × 39 + 0 × 11
BS(B) = 2 × 39 + t × 31 + 0 × 11
如果要讓 BS(A) > BS(B)
那麼將有 t > 2
Fishburn Theorem
-
在候選人數量大於等於3名時,沒有任何計數法能夠總是達到孔多賽規則的效果。
不過
孔多賽並不是一個完全合理的規則

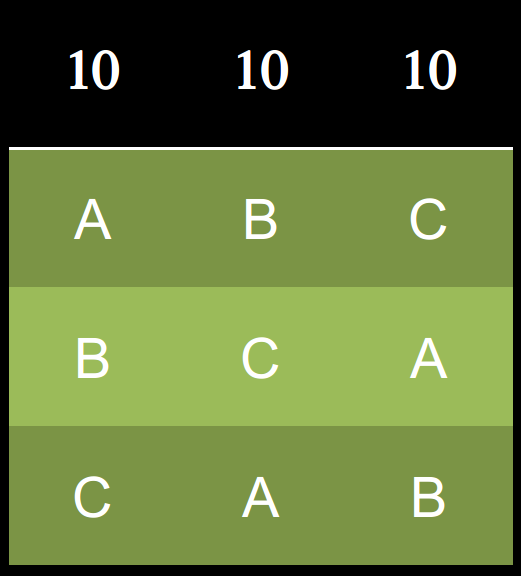
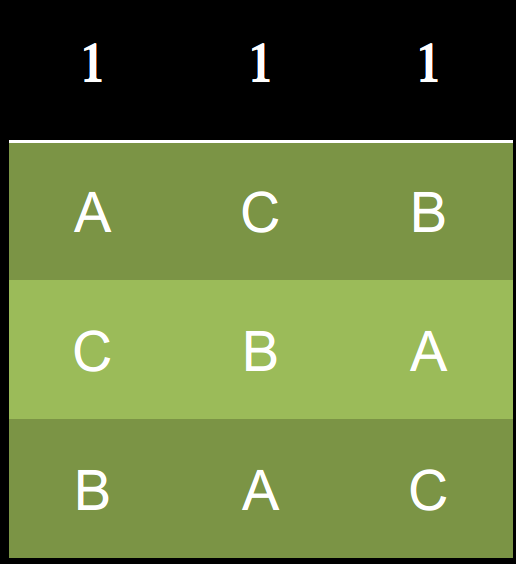
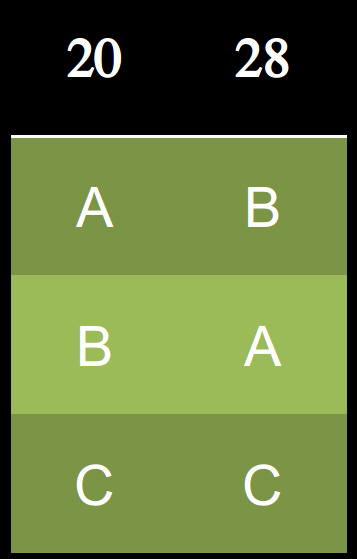
循環
循環
B勝
A是孔多賽溫拿
分組
逐步淘汰法
也有滿有趣的悖論
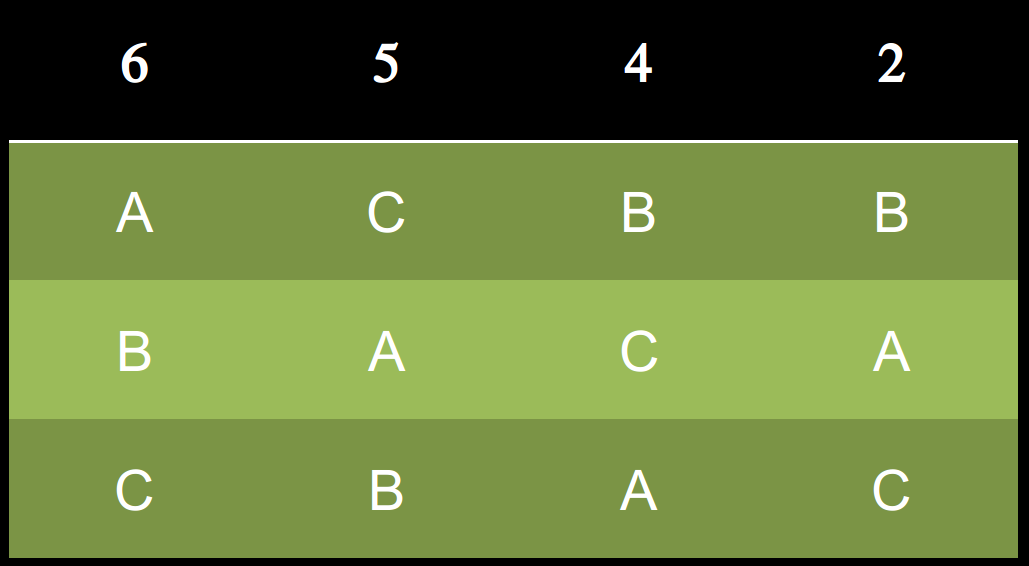
A勝出
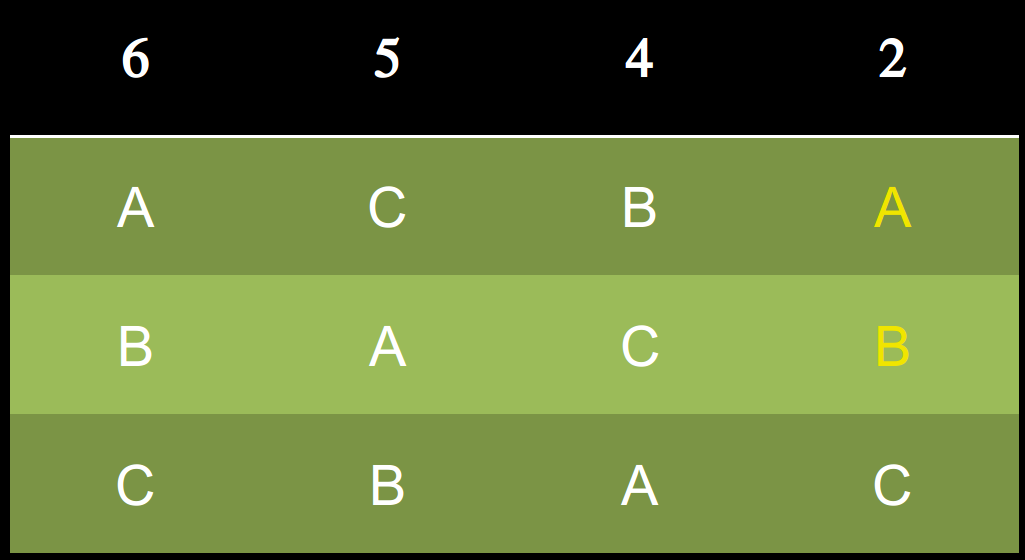
C 勝出

B 勝出
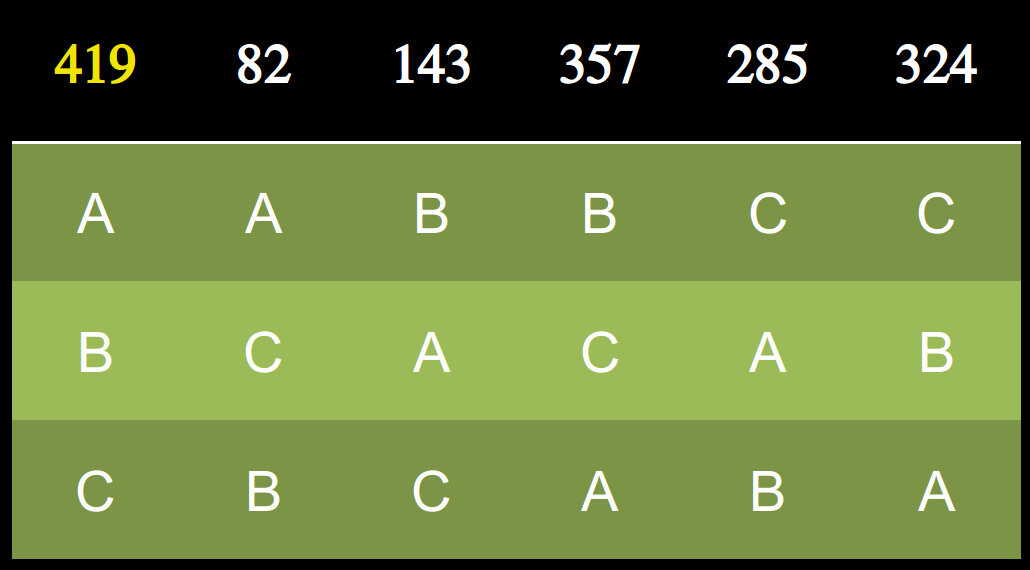
C 勝出
今天介紹的方法總結
-
共識決
- 異議的處理
-
投票
- 多數決規則
- 孔多賽規則
- 逐步淘汰法
- 伯達計數法

多數決依然是我們在民主社會中最常使用的投票法
「策略性投票」作為平衡
凸顯了媒體的重要性
- 「棄X保O」
- 「XX軍整合」
- 「黨內初選」
- 「懶得出門」
- 均以「民調」作為基礎
Gibbard-Satterthwaite Theorem
在自然假設下,沒有任何投票法能保證投票者會誠實地投票。
投票不只是一個單純的
公平分析的問題
-
是一個社會問題
投票法必須能被社會成員所理解
-
是一個政治問題
必須同時考慮投機投票和有心人士的操弄
-
是一個科技問題
有越好的演算法,可以計算越複雜的投票法
什麼時候採用什麼方法?
- 自然解決
- 授權處理
- 共識決
- 比賽
-
投票
- 選擇方法
Thank You
