Isolated Black Hole from Astrometric Microlensing(?)

Wei Zhu (祝伟)

Tsinghua Astro Student Seminar

2022 March 4

Sahu et al. (2022) & Lam et al. (2022)

Outline

  • Microlensing detecting dark objects
    • Opportunity & challenges

 

  • OGLE-2011-BLG-0462
    • The first dark object from astrometric microlensing?

 

  • Summary

微引力透镜 (Gravitational microlensing)

Einstein (1936); Paczynski (1986); Mao & Paczynski (1991)

\(t_{\rm E} \sim 30{\rm days} \left(\frac{M_{\rm L}}{M_\odot}\right)^{1/2} \)

\( t_q \sim 40{\rm min} \left(\frac{q}{10^{-6}}\right)^{1/2} \left( \frac{t_{\rm E}}{30 \rm days}\right) \)

背景恒星亮度

背景恒星

”透镜“星体

\( t_{\rm E} \)

\( t_q \)

First microlensing BH candidate?

Mao et al. (2002)

(see also Bennett+2002, Agol+2002)

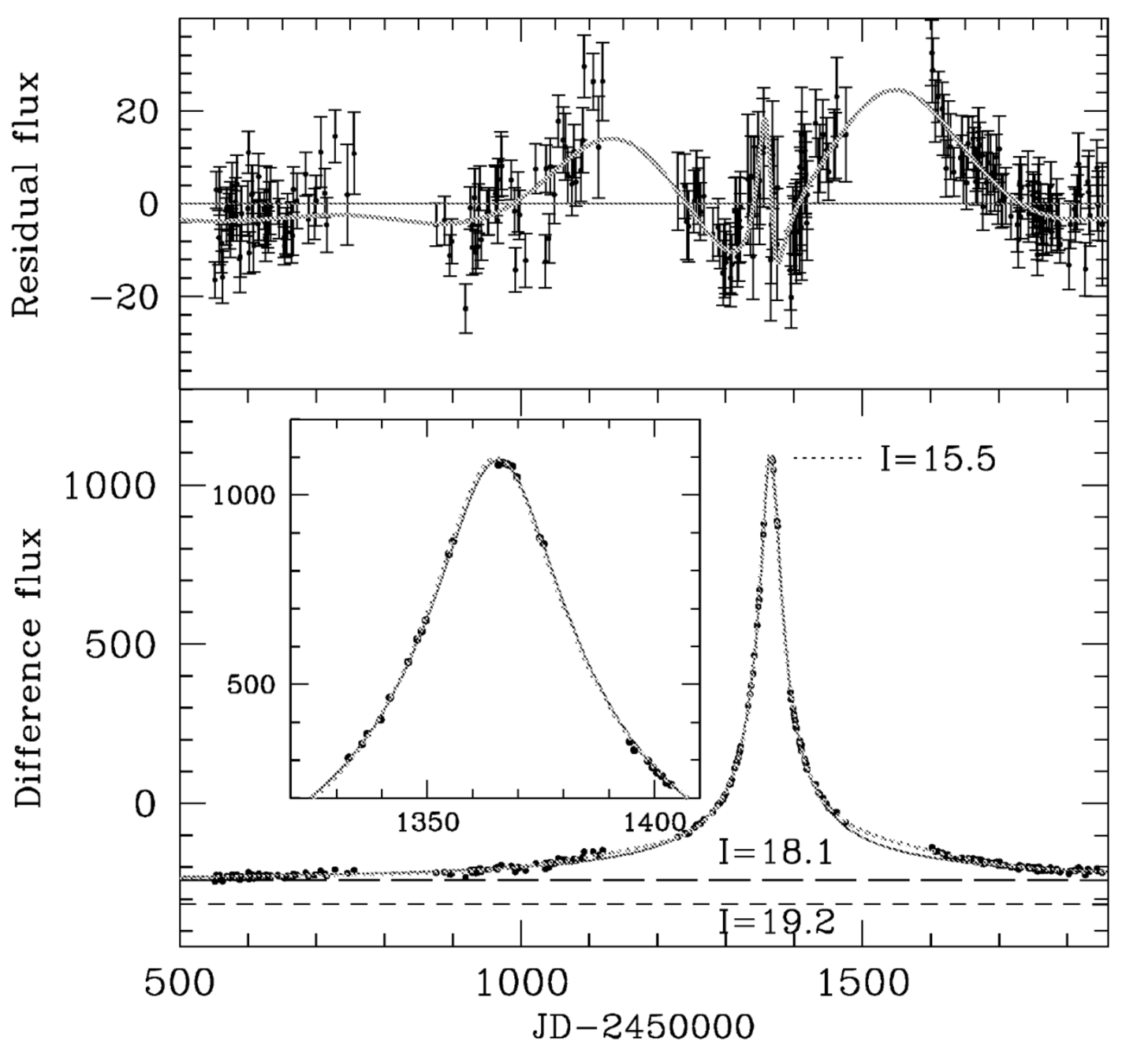
OGLE-1999-BUL-32: \( t_{\rm E} = 640 \) days

\( t_{\rm E} = \frac{\theta_{\rm E}}{\mu_{\rm rel}} \approx f(M_{\rm L}, D_{\rm L}, \mu_{\rm rel}) \)

A statistical approach

Sumi et al. (2011)

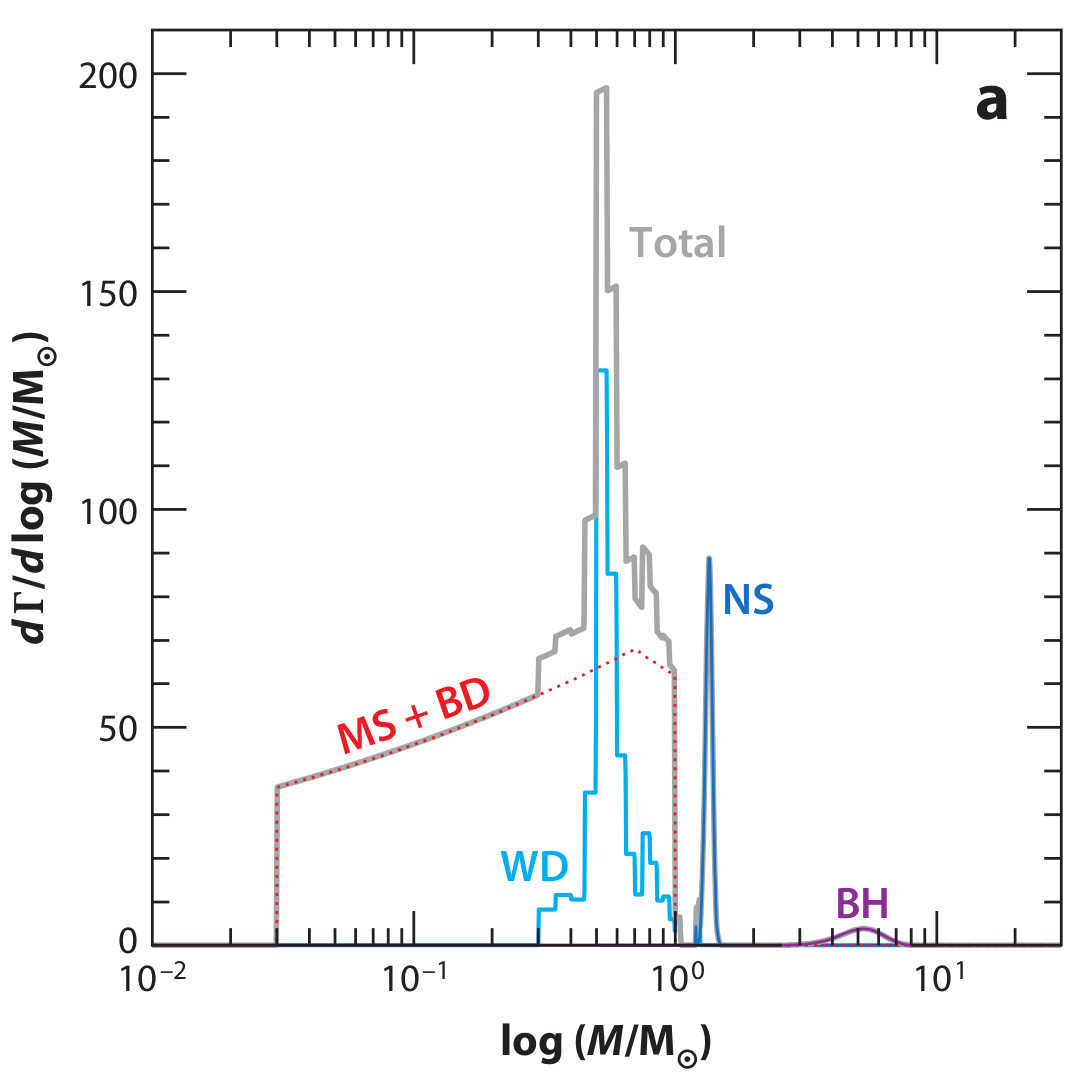
Nature of microlenses

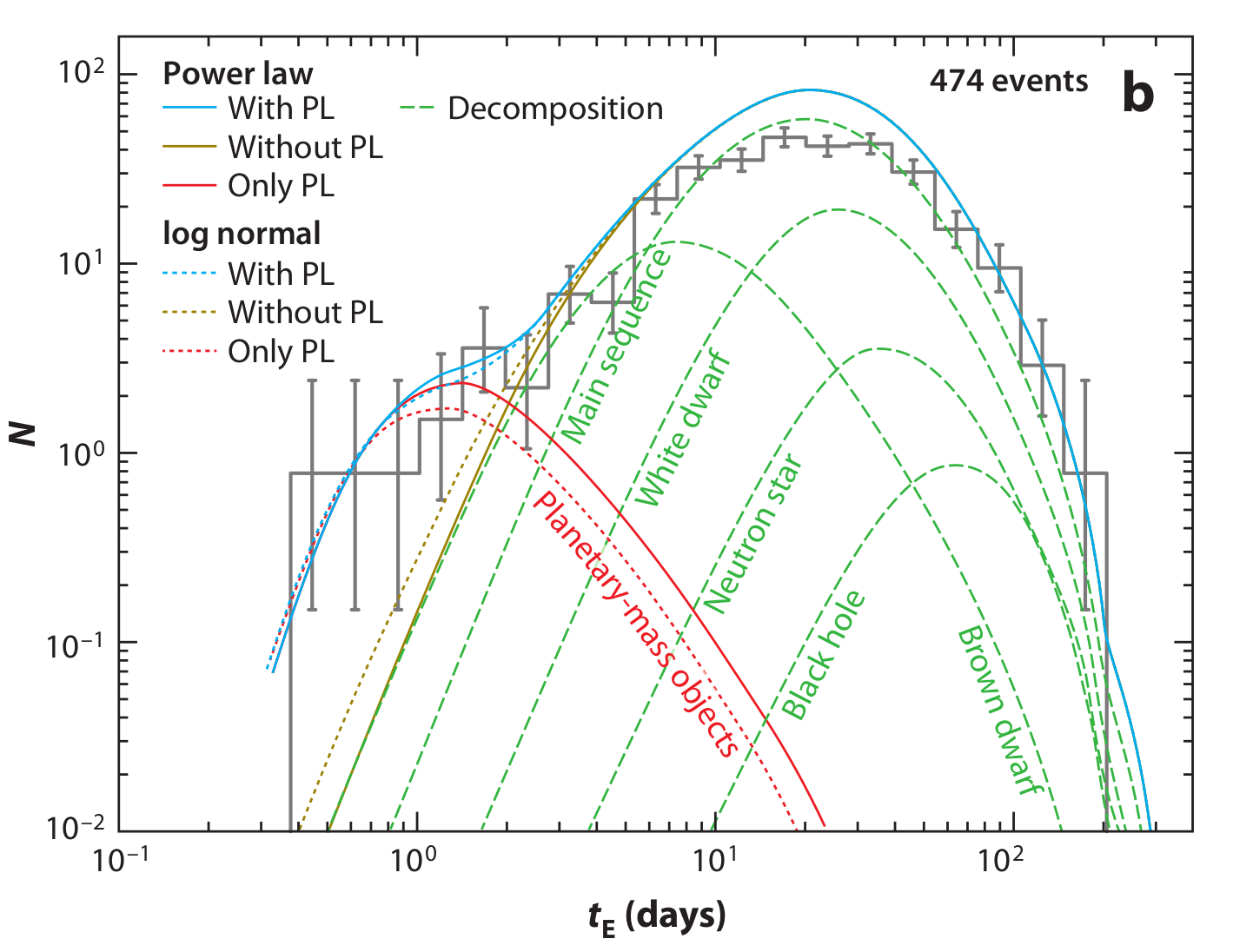
Microlensing toward the bulge:

White dwarf (WD): 17%

Neutron star (NS): 3%

Black hole (BH): 1%

Gaudi (2012)

(see also Gould 2000)

How can we tell BH lenses from normal lenses?

$$ M_{\rm L} \propto \frac{\theta_{\rm E}}{\pi_{\rm E}} $$

Microlensing parallax

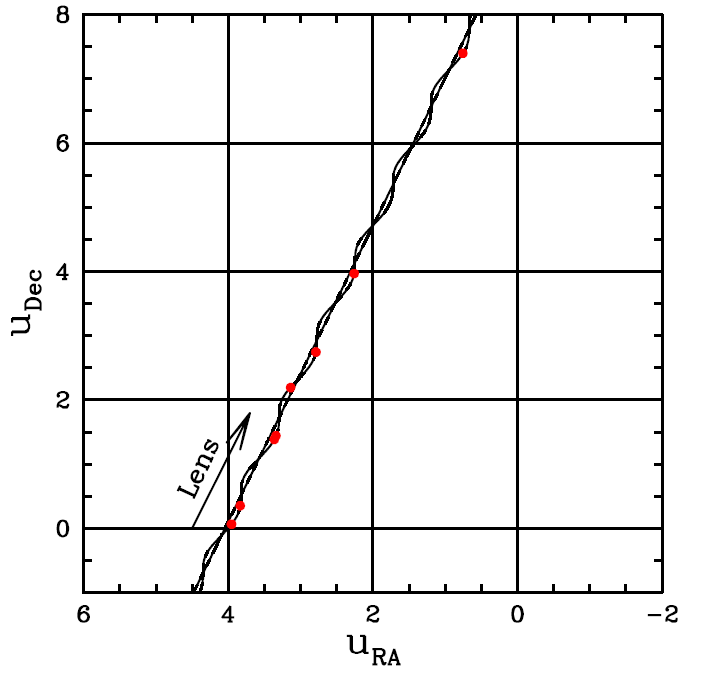
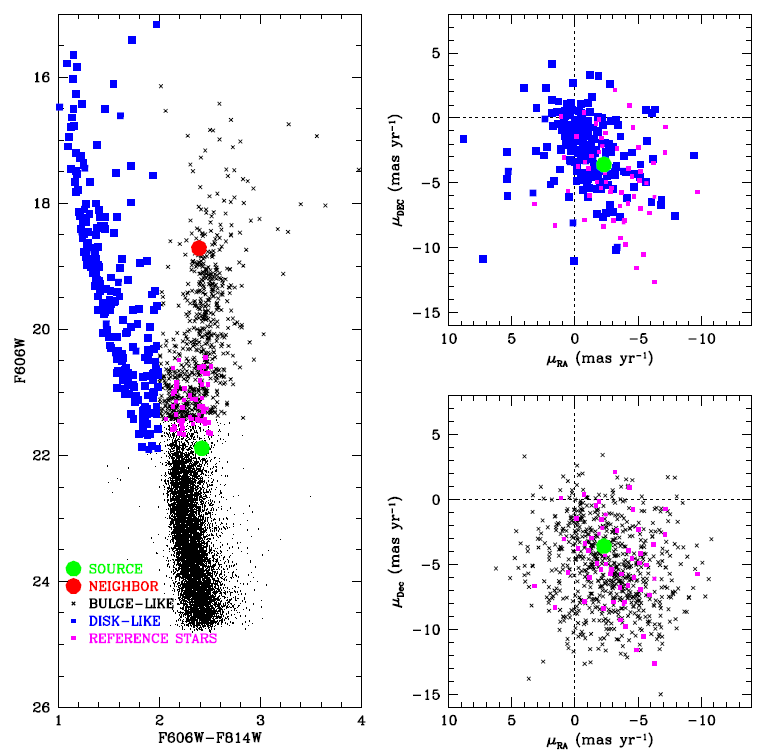
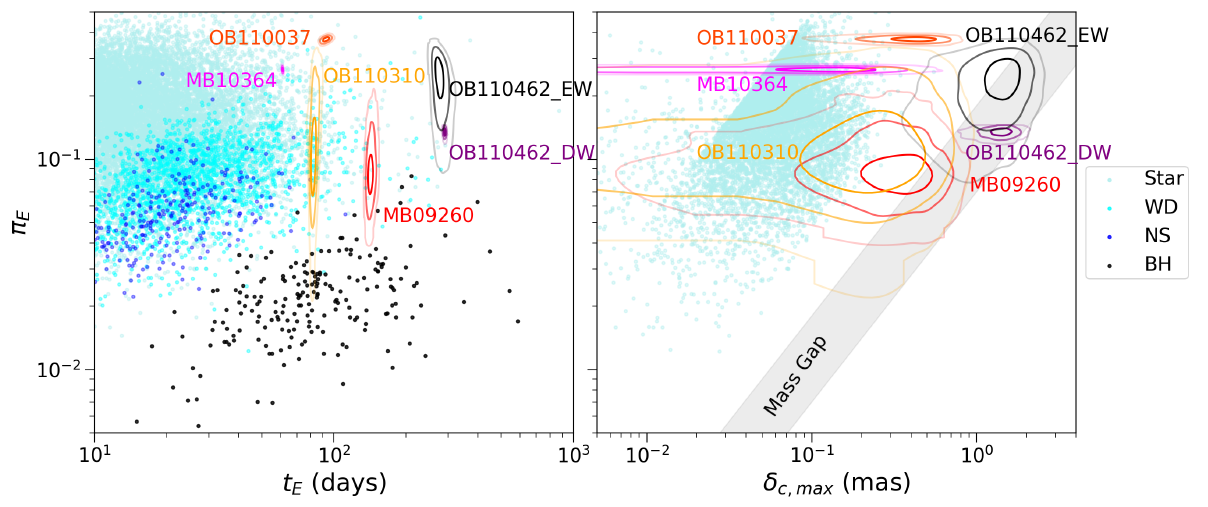
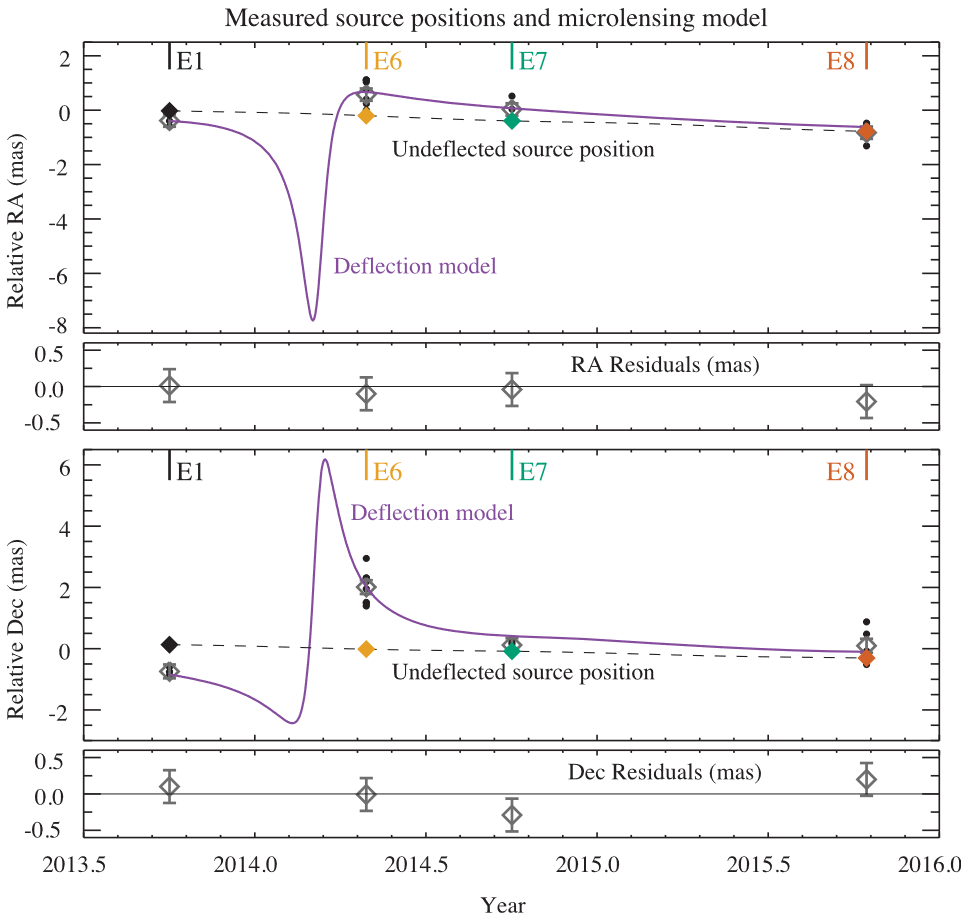
Figures from Sahu et al. (2022, left) and Wyrzykowski et al. (2016, right)

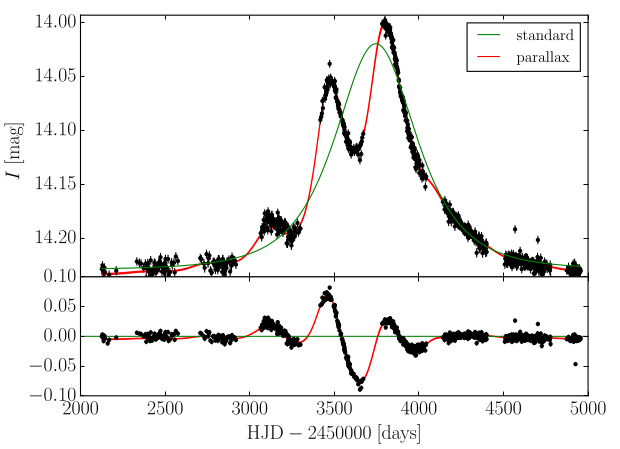
Microlensing parallax: an observable more sensitive to mass

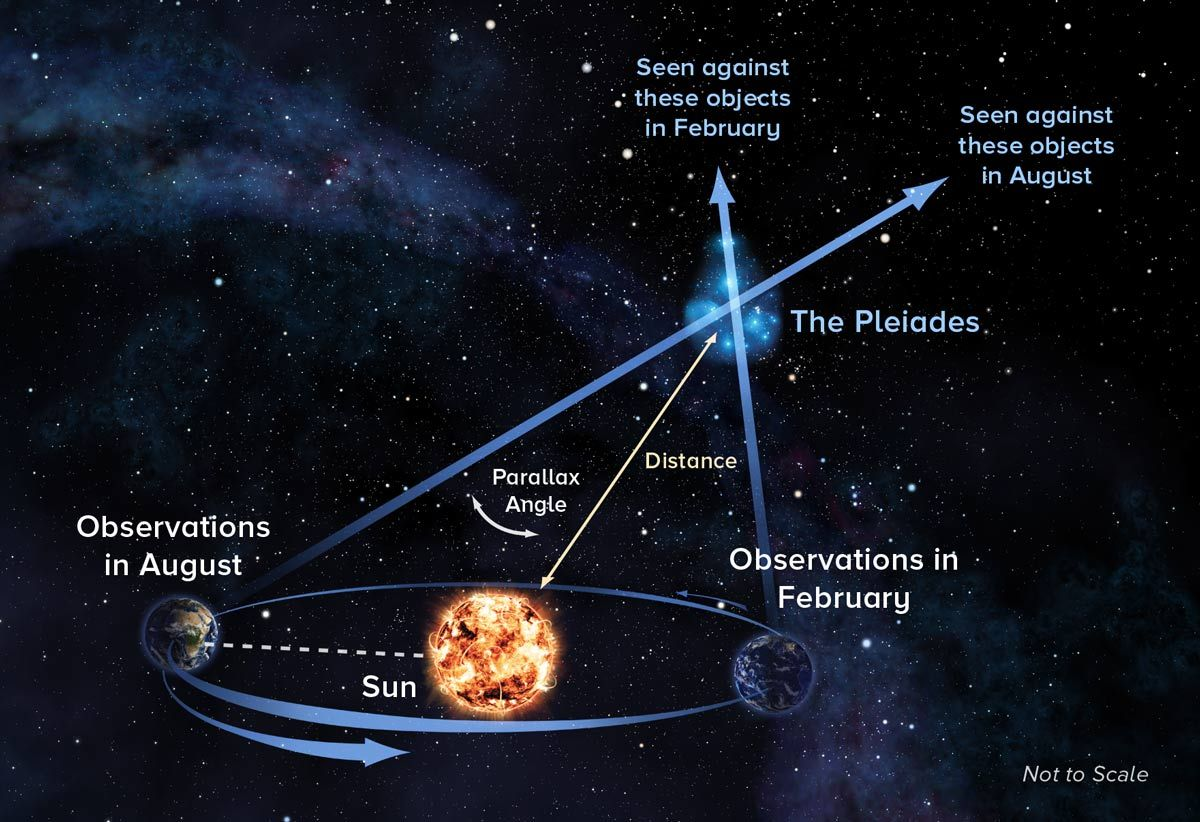
Image credit: Bill Saxton, NRAO/AUI/NSF

  • Parallax (absolute): \( \pi \equiv \frac{\rm au}{d} \)
  • Microlensing parallax: $$ \pi_{\rm E} \equiv \frac{\pi}{\theta_{\rm E}} \approx f(M_{\rm L}, D_{\rm L})$$

Parallax effect in BH event

Lam et al. (2020)

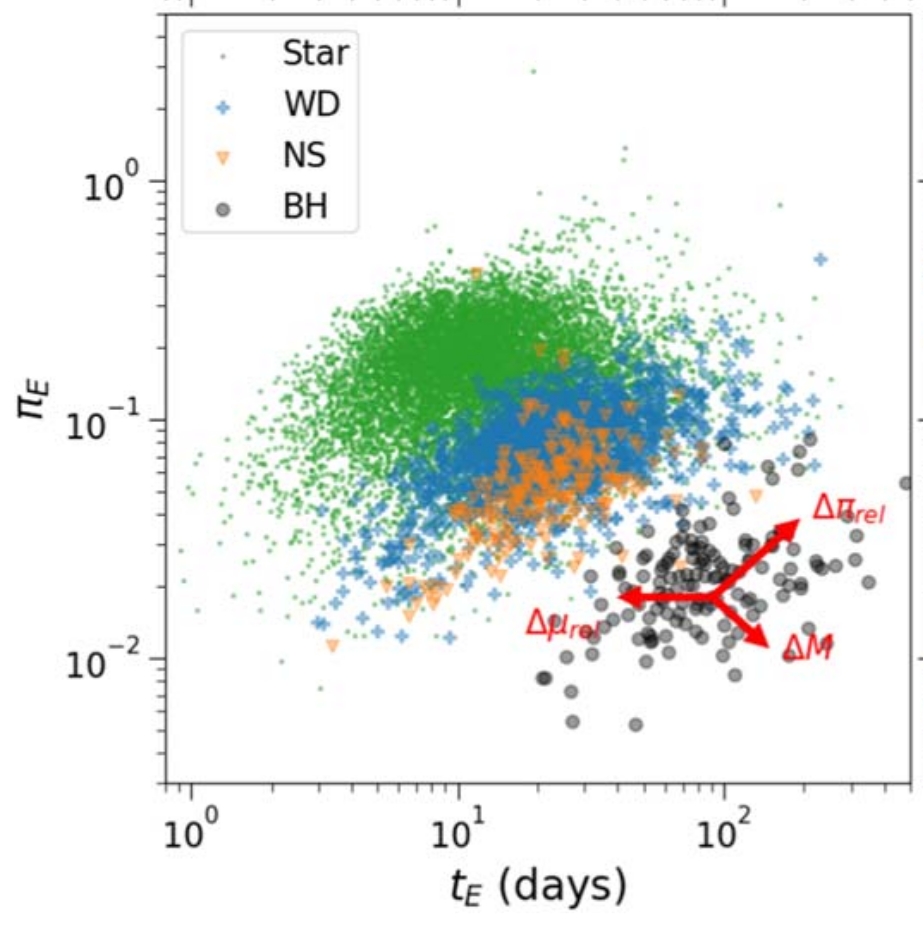
Typical BH events have

  • long timescales (\(t_{\rm E} \gtrsim 100 \) d);
  • small parallaxes (\(\pi_{\rm E} \lesssim 0.05\));
    • usually undetectable (Karolinski & Zhu 2020; Ma, Zhu, & Yang, 2022).

\(\theta_{\rm E}\) from Astrometric microlensing

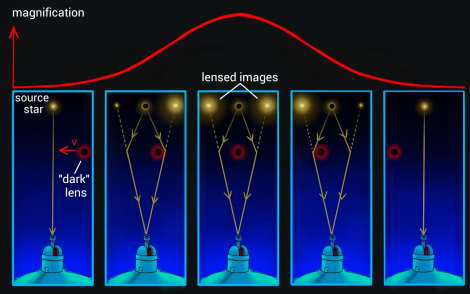
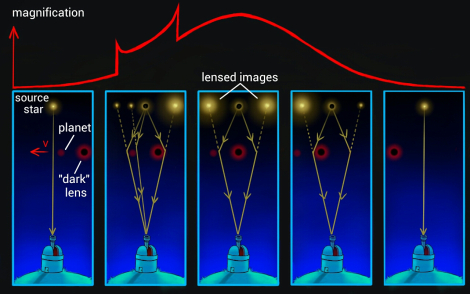
Animations credit to: B. Scott Gaudi (see also Dominik & Sahu 2000)

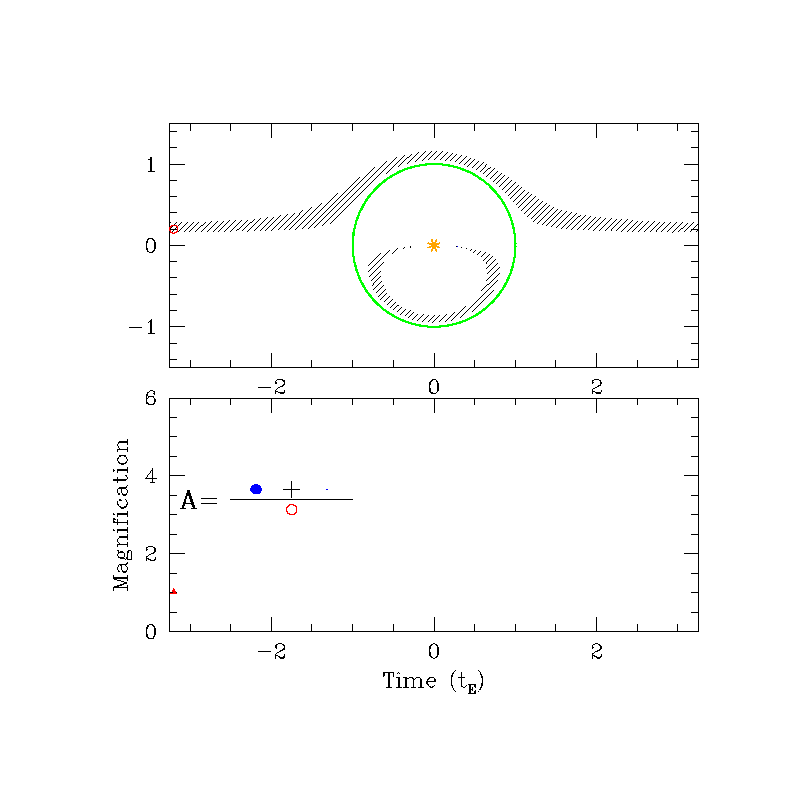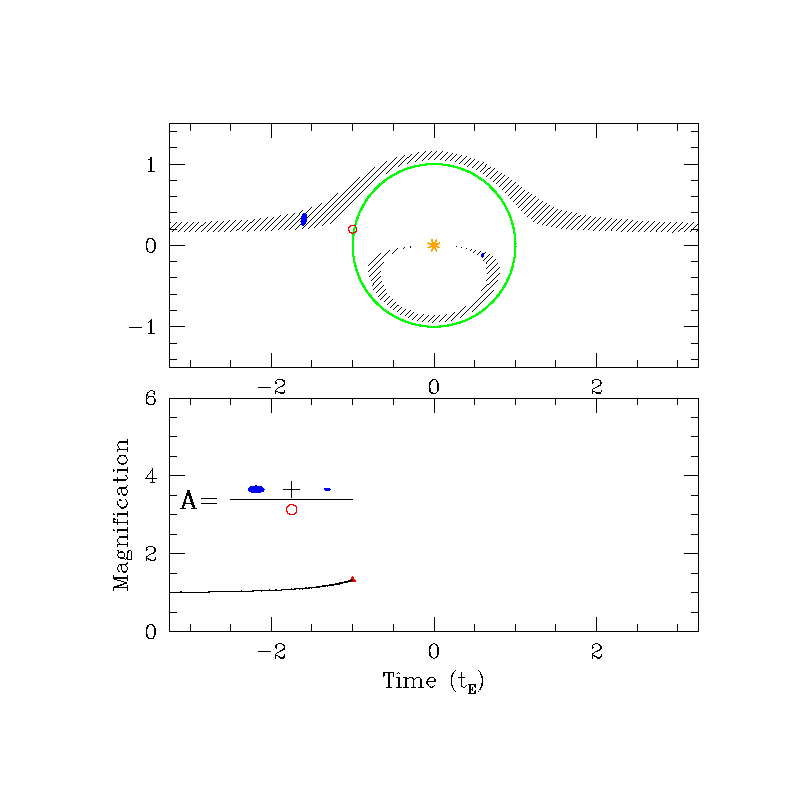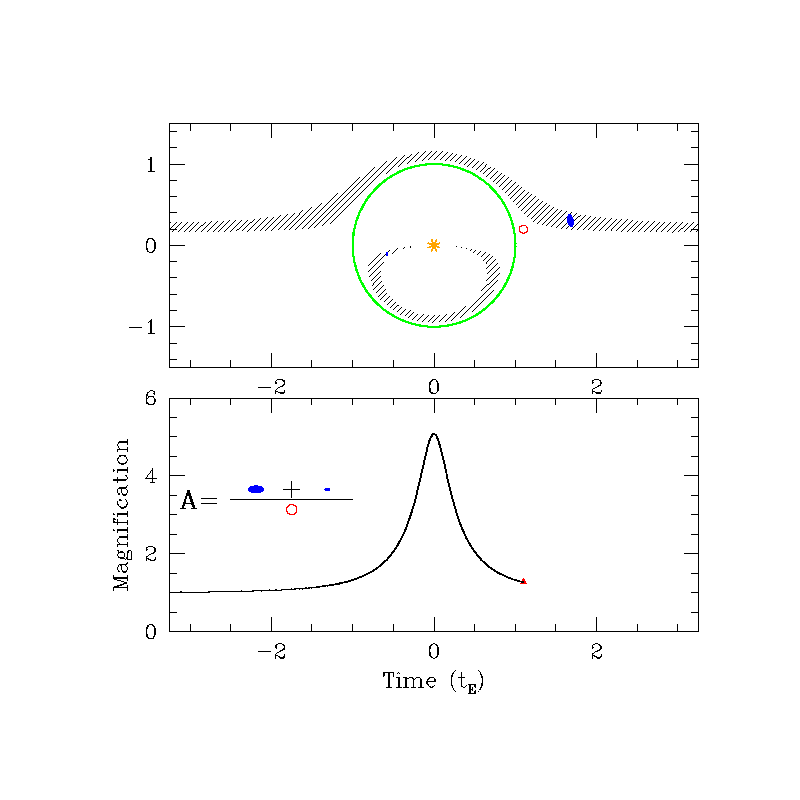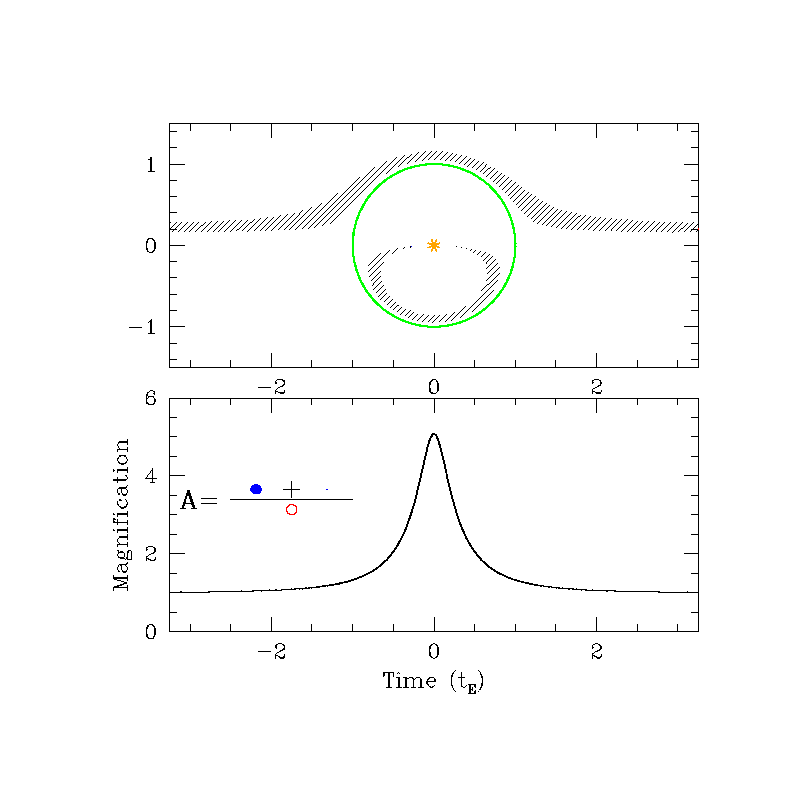
Photometric

Animations credit to: B. Scott Gaudi (see also Dominik & Sahu 2000)

Photometric

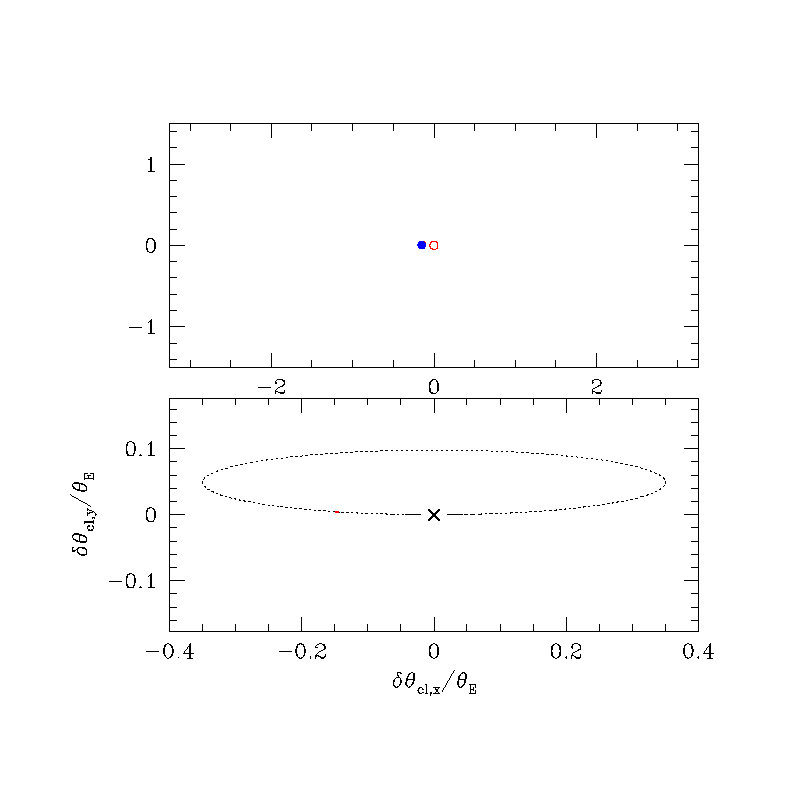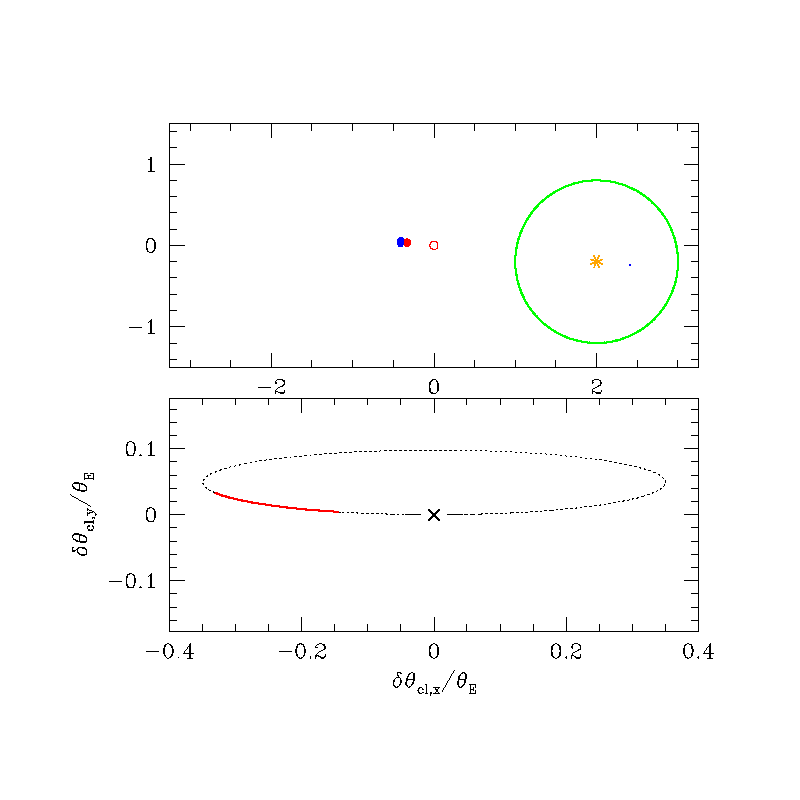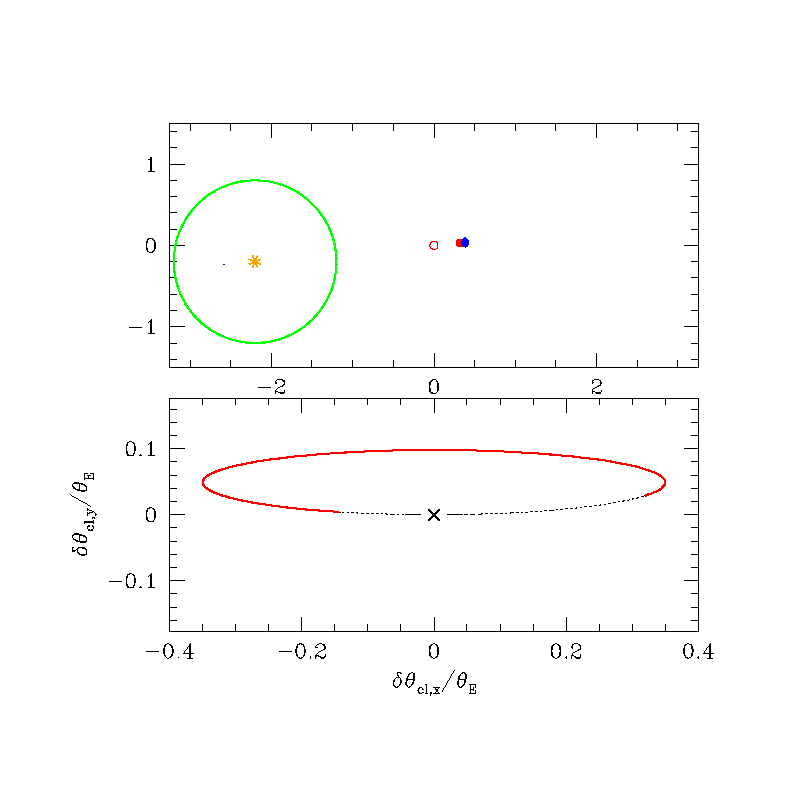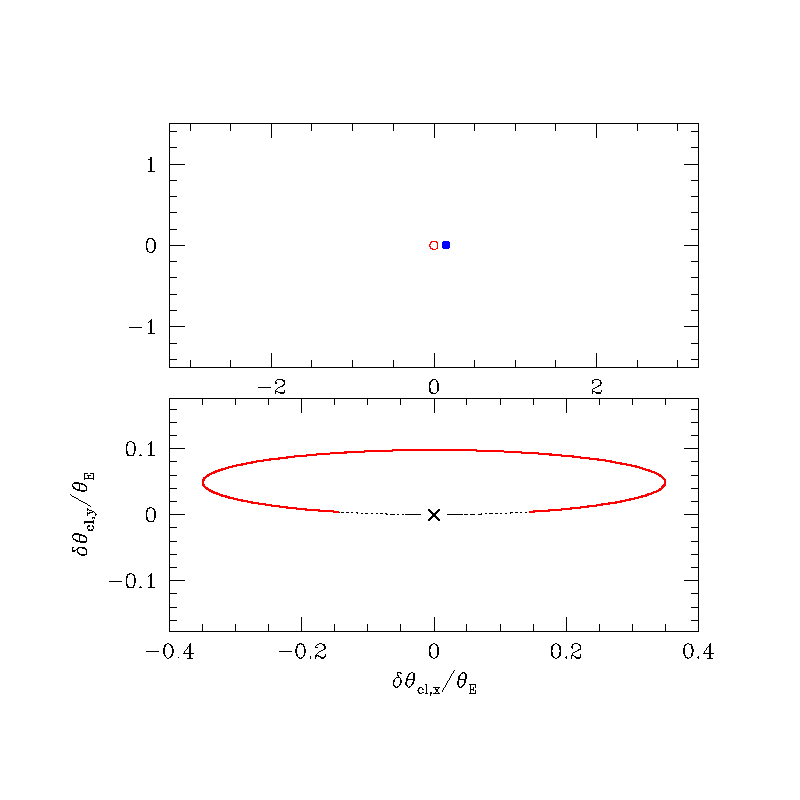
Astrometric (source frame)

Astrometric (lens frame)

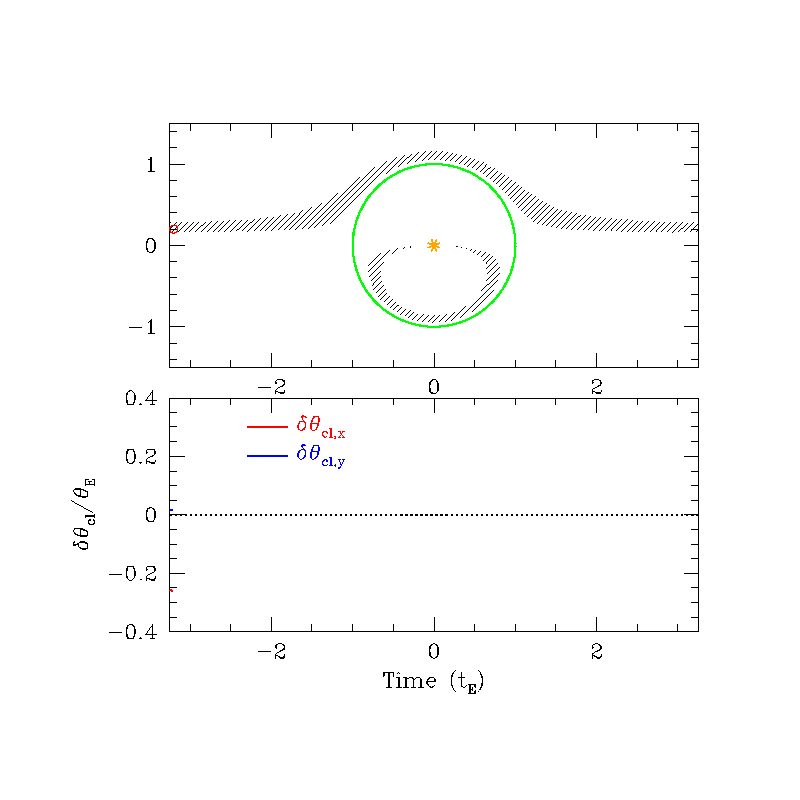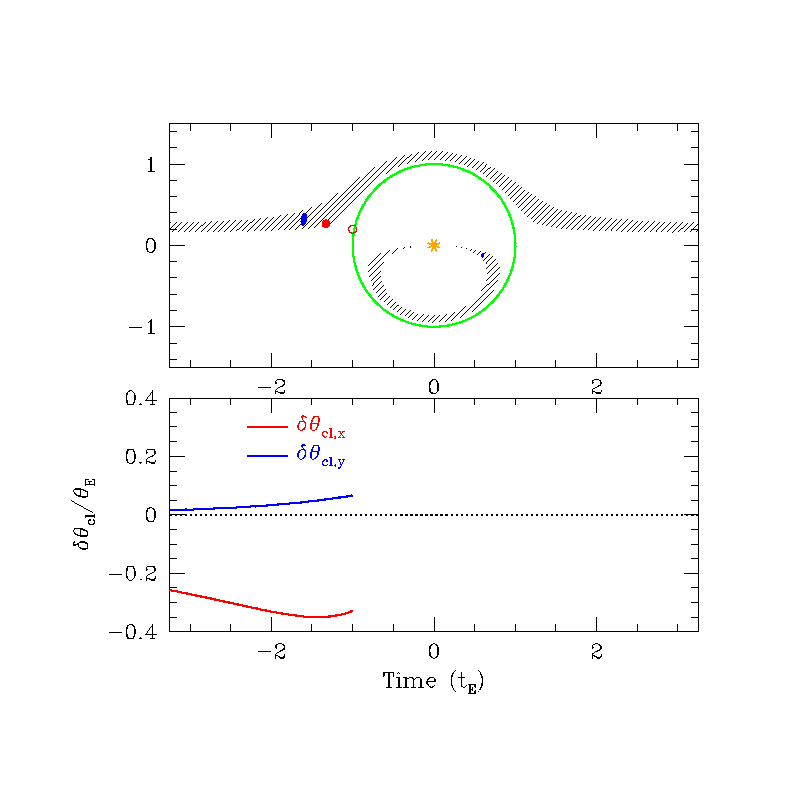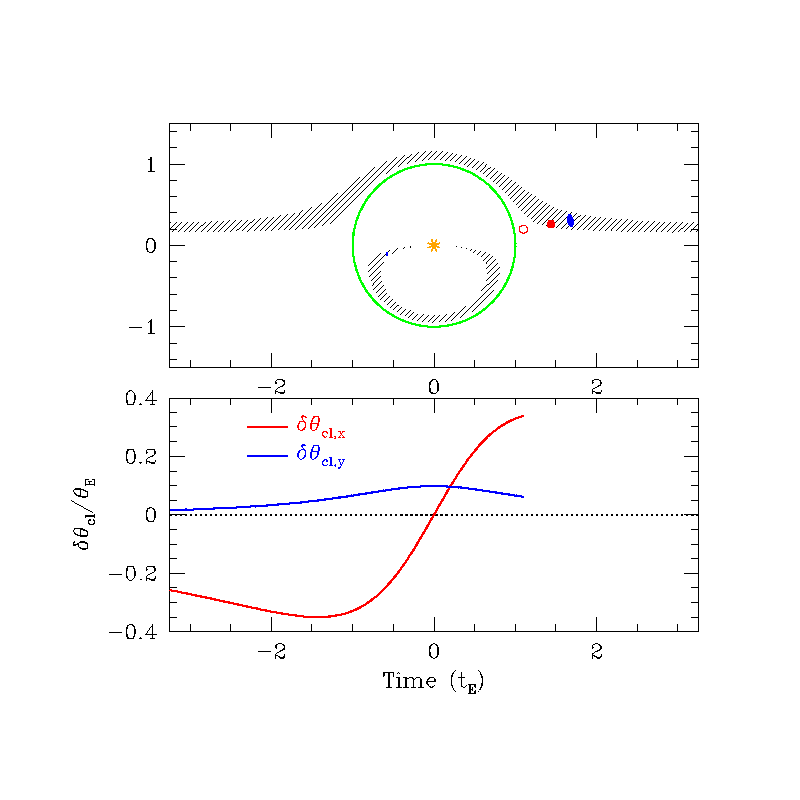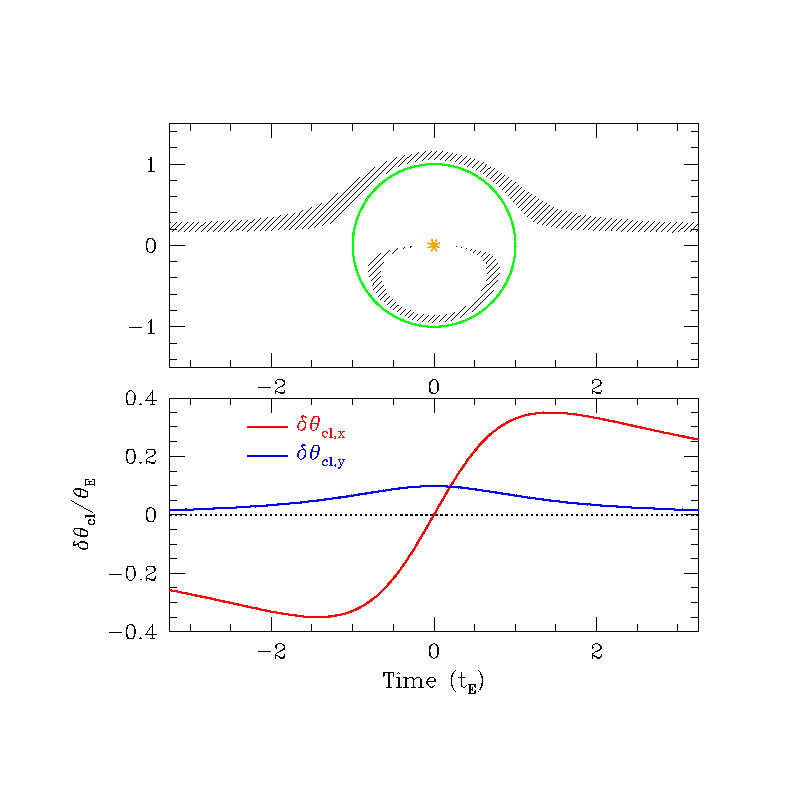
\( \delta_{\rm max} (u=\sqrt{2}) = \frac{\sqrt{2}}{4} \theta_{\rm E} \approx 0.35 \theta_{\rm E} \)

\(\theta_{\rm E}\) from Astrometric microlensing

Previous attempts

Sahu et al., 2017, Science

(see also Lu+16, Kains+17)

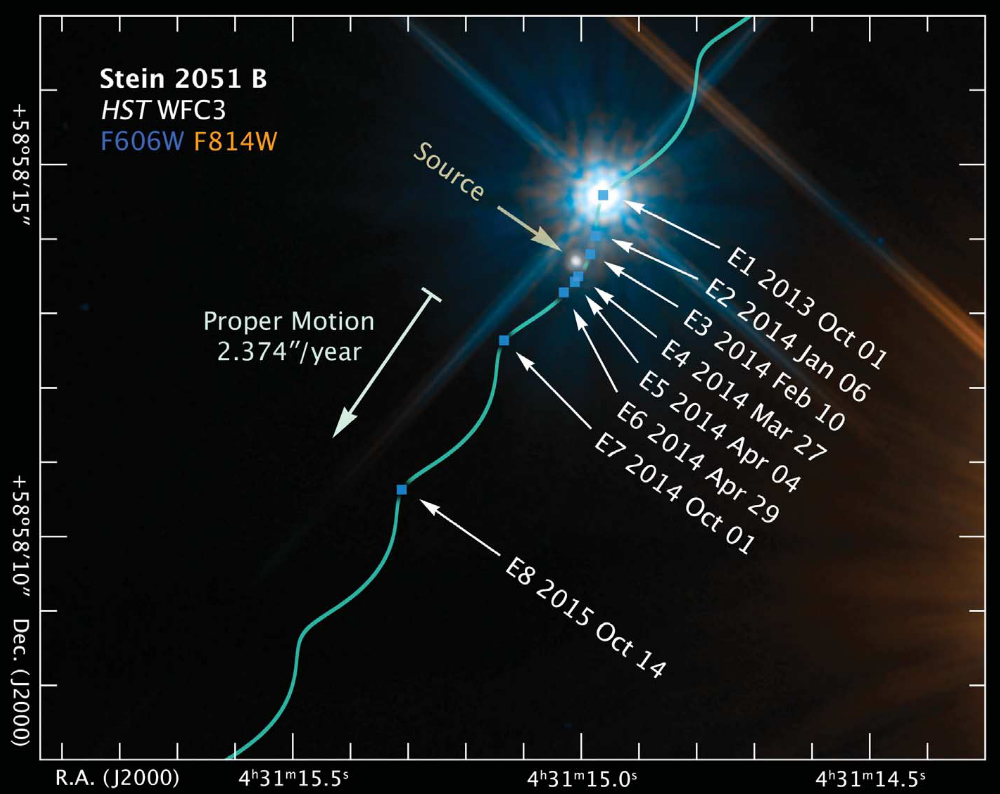
Previous attempts

Sahu et al., 2017, Science

(see also Lu+16, Kains+17)

Astrometric microlensing detecting dark object

Precise astrometry on

  • Long timescale events
  • Bright & isolated source star

 

Constraints on

  • Angular Einstein radius \(\theta_{\rm E}\)
  • Relative proper motion

Take-home message

Long-timescale event, OGLE-2011-BLG-0462, was caused by a dark object, probably an isolated stellar-mass black hole, based on HST astrometric microlensing and ground-based photometry.

The key difference came from photometric microlensing signal (\(\pi_{\rm E}\)), not astrometric microlensing signal (\(\theta_{\rm E}\)).

OGLE-2011-BLG-0462 (OB110462)

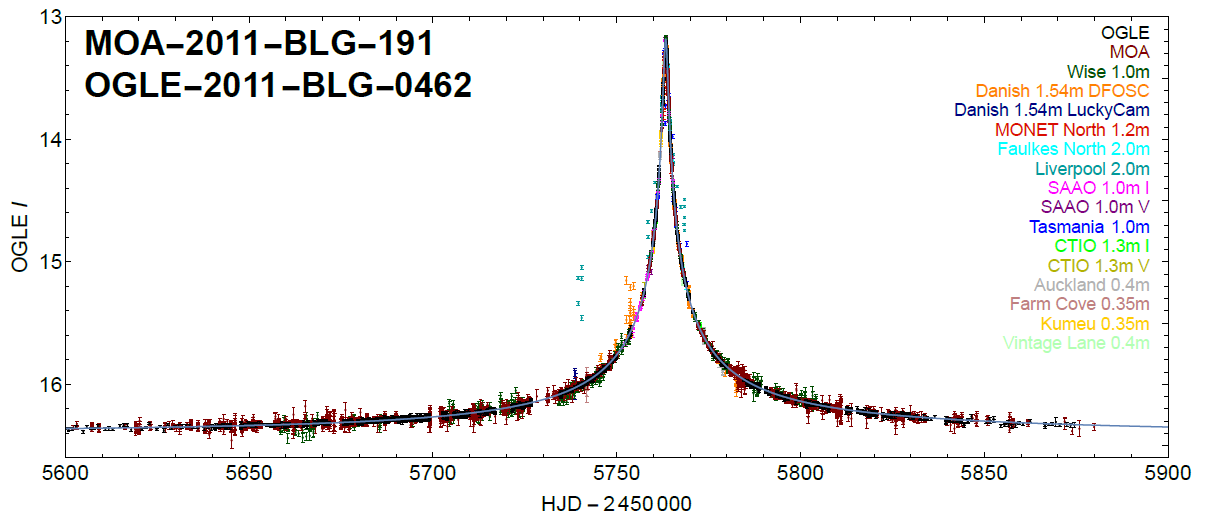
Light curve plot from Sahu et al. (2022)

\( A_{\rm max}=372.62 \)

\( t_{\rm E}=231.56\) days

First HST observation

Imaging (OGLE vs. HST)

2'

8"

2"

HST observations

WFC3 F606W & F814W filters.

Additional observations obtained in Lam et al.

HST astrometric analysis

  • Reference frame
    • Gaia frame

 

  • Bias correction due to nearby star (~0.4 mas)
    • Reconstructed PSF vs. injection-recovery exercise

 

  • Astrometric color offset

Astrometric signal (Sahu et al.)

F606W

F814W

Angular Einstein radius \( \theta_{\rm E} = 5.18 \pm 0.51 \) mas

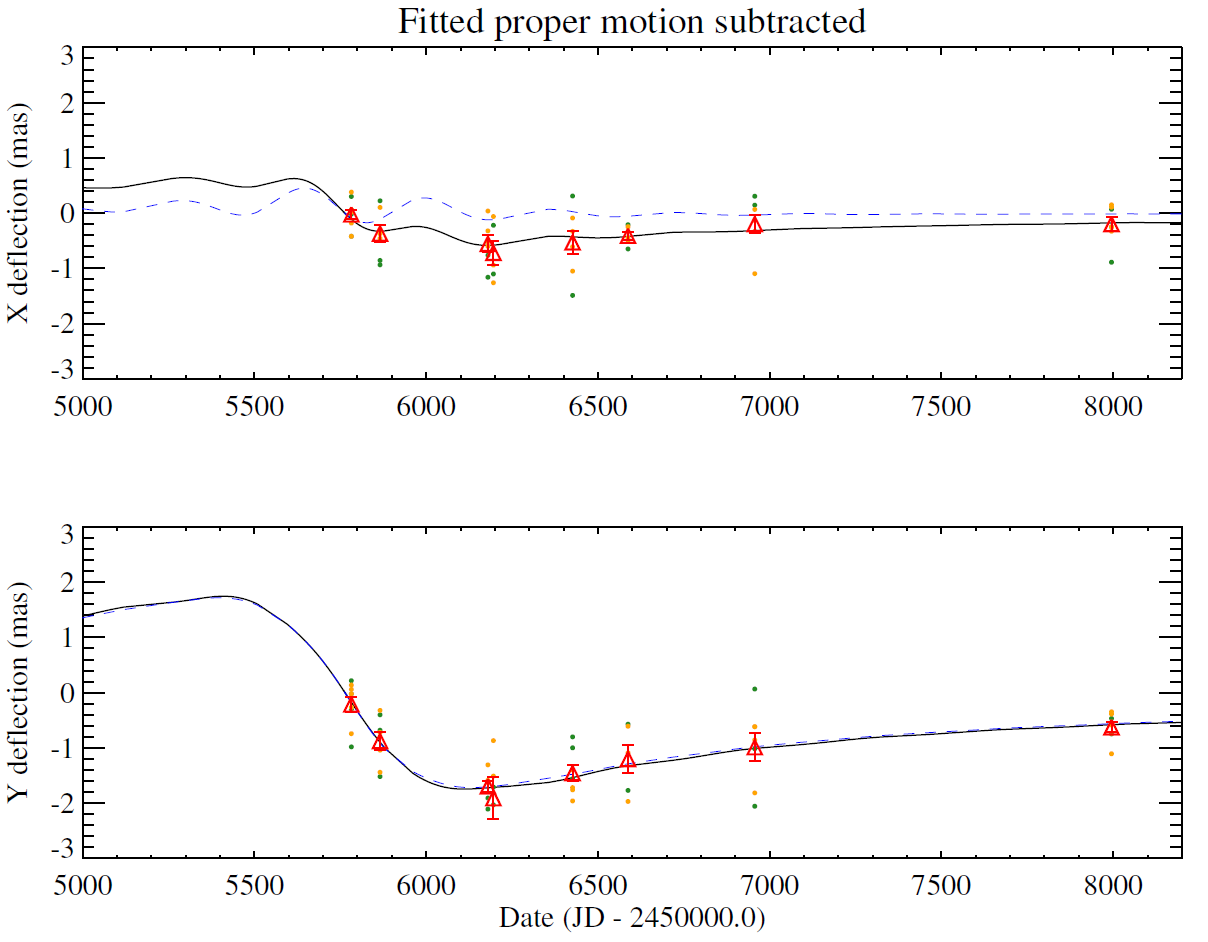
Astrometric signal (Lam et al.)

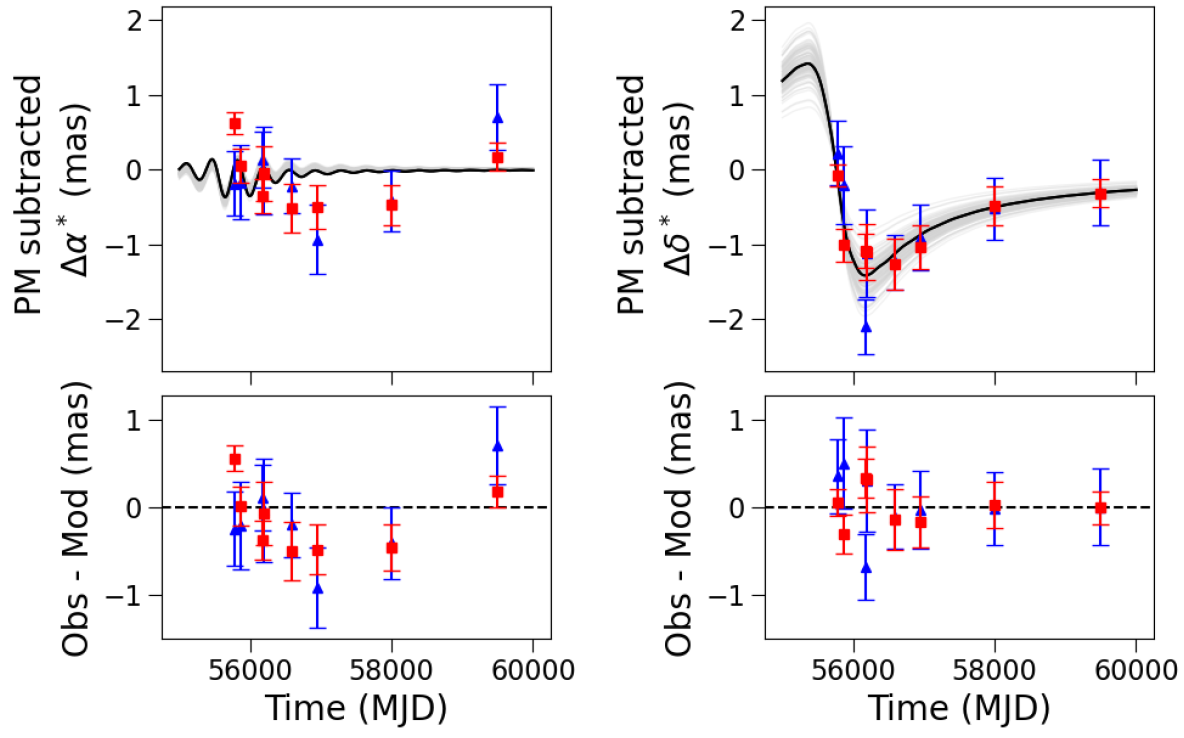
F606W

F814W

Angular Einstein radius \( \theta_{\rm E} = 4.0 \pm 1.1 \) mas

Astrometric microlensing

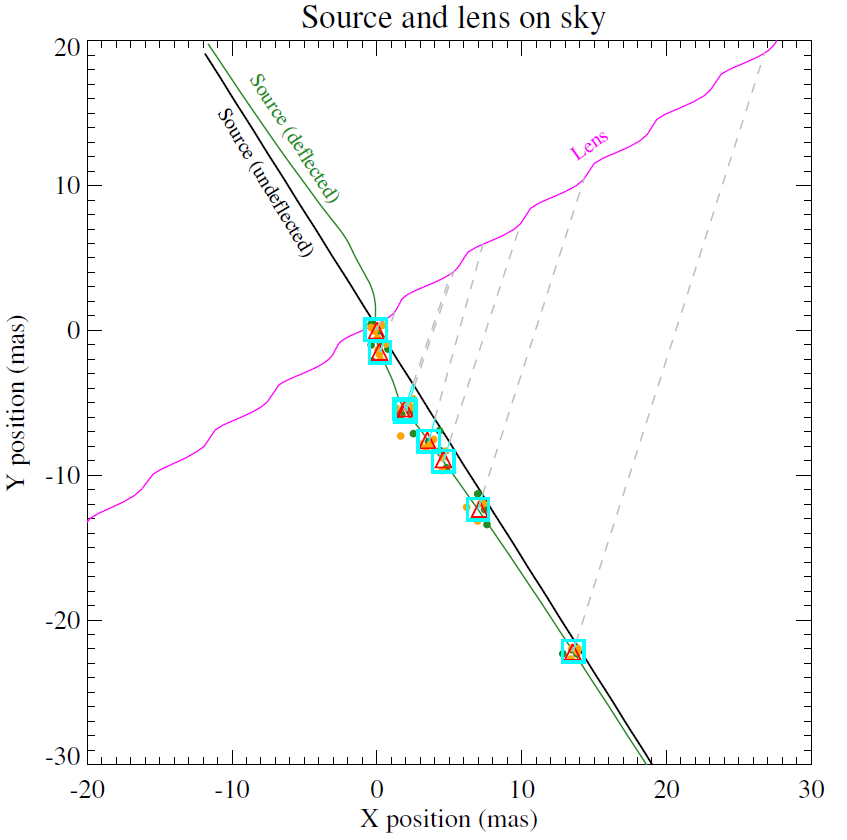
Angular Einstein radius

\( \theta_{\rm E} = 5.18 \pm 0.51 \) mas (Sahu et al.)

\( \theta_{\rm E} = 4.0 \pm 1.1 \) mas (Lam et al.)

Figure from Sahu et al. (2022)

Photometric microlensing

Microlensing parallax

\( \pi_{\rm E}=0.089 \pm0.014 \) (Sahu et al.)

\( \pi_{\rm E} = 0.13 \pm0.01 \) or \( 0.24 \pm 0.05\) (Lam et al.)

Mass determination

Sahu et al. Lam et al.
Angular Einstein radius (mas) 5.18+-0.51 4.0+-1.1
Microlensing parallax 0.089+-0.014 0.13+-0.01 or
0.24+-0.05
Lens mass (M_sun) 7.1+-1.3 [1.6, 4.5]
Lens distance (kpc) 1.58+-0.18 [0.9, 1.5]

\( M_{\rm L} = 1.2 M_\odot \left( \frac{\theta_{\rm E}}{\rm mas} \right) \left( \frac{\pi_{\rm E}}{0.1} \right)^{-1} \)

Summary

  • Microlensing detecting dark objects
    • Opportunity: unique in detecting isolated dark objects
    • Challenge: direct mass determination (via parallax & Einstein radius)

 

  • OGLE-2011-BLG-0462: The first dark object from astrometric microlensing
    • HST astrometric microlensing yielding Einstein radius
    • Ambiguity in microlensing parallax

Back-up slides

Made with Slides.com