\(H_0\) from strong lensing time delay
(Based on Wong et al. 2019 and Kochanek 2020)
Wei Zhu (祝伟)
2020-04-30
\(H_0\) Lenses in COSMOGRAIL's Wellspring (H0LiCOW )


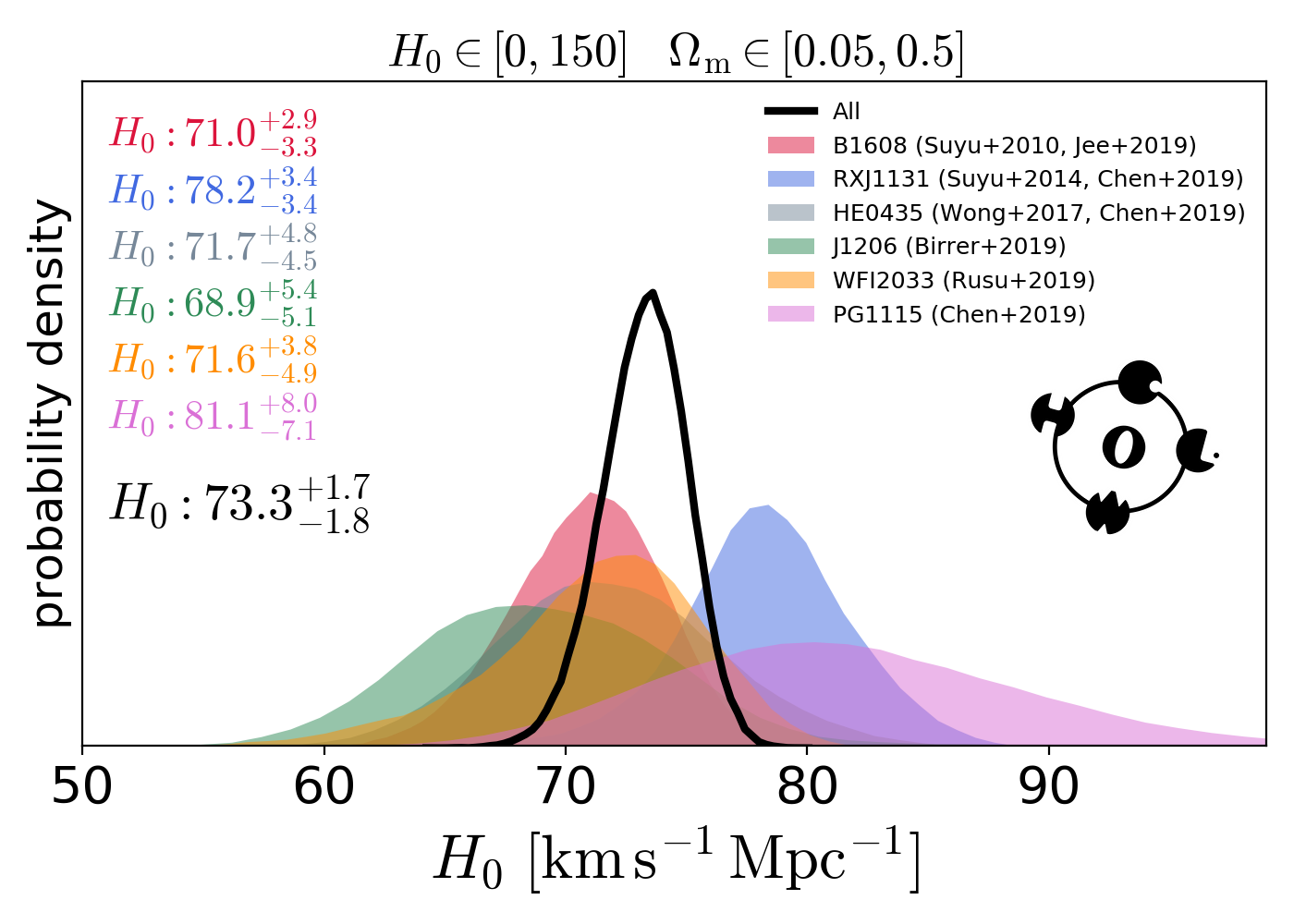
- 2.4% error on \(H_0\);
- 5.3\(\sigma\) tension with CMB \(H_0\).
How to measure \(H_0\) from strong lensing (1)


\(D_S\)
\(D_L\)
\(D_{LS}\)

\(\beta\)
\(\alpha\)
\(\hat{\alpha}\)
\(r_{\perp}\)

Source
Image
Lens
- Lens equation
$$ \vec{\beta} =\vec{\theta} - \vec{\alpha} = \vec{\theta} - \frac{D_{LS}}{D_S} \vec{\hat{\alpha}} $$
- Deflection angle
$$ \hat{\alpha} = \frac{4GM(<r_\perp)}{c^2 r_\perp};\quad r_\perp=D_L\theta $$
- Perfect alignment \(\vec{\beta}=\vec{\theta_E} - \vec{\alpha}(\vec{\theta_E})=0\)
- Einstein radius \(\theta_E\)
- Critical surface density \(\Sigma_{\rm crit} \equiv \frac{M(<r_\perp)}{\pi r_\perp^2}\)
- Convergence \(\kappa \equiv \frac{\Sigma}{\Sigma_{\rm crit}} \)
\(\theta\)
Lensing geometry alone does not provide a distance scale (L=VT).
How to measure \(H_0\) from strong lensing (2)


\(D_S\)
\(D_L\)
\(D_{LS}\)

\(\beta\)
\(\alpha\)
\(\hat{\alpha}\)
\(r_{\perp}\)

Source
Image
Lens
- Lensing time delay
- Time delay distance
$$ D_{\Delta t} \equiv (1+z_L) \frac{D_L D_S}{D_{LS}} $$
- Lensing potential
$$\nabla_{\theta} \psi(\theta) = \vec{\alpha} $$
$$\nabla^2_{\theta} \psi(\theta) = 2\kappa(\theta) $$
- Time delay between two images
$$ \Delta t \propto H_0^{-1} (1-\langle \kappa \rangle ) $$
- Usually, \(\langle \kappa\rangle \approx \kappa (\theta_E) \equiv \kappa_E\).
\(\theta\)
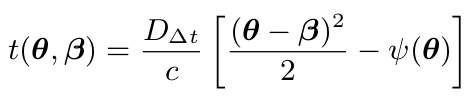

Without information about the lens density distribution (\(\kappa\)), time delay itself does not measure \(H_0\).
H0LiCOW

- Spectroscopy to get kinematics of the lens galaxy.
- Assuming certain density profile, extrapolate to the lensing region (i.e., Einstein radius).
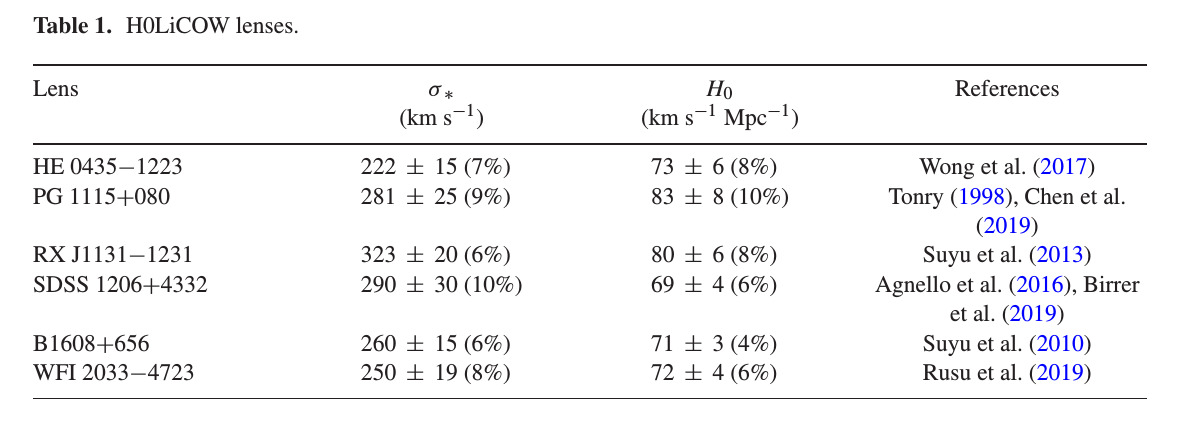
If uncertainty is dominated by kinematics, \(\sigma(H_0) = \sigma(\kappa) \approx \sigma(\sigma_\star^2) =2\sigma(\sigma_\star) \).
Why H0LiCOW \(H_0\) is so "precise"


\(D_S\)
\(D_L\)
\(D_{LS}\)

\(\beta\)
\(\alpha\)
\(\hat{\alpha}\)
\(r_{\perp}\)

Source
Image
Lens
\(\theta\)
- Lens has a simple power-law density profile \(\rho \propto r^{-n} \).
- Image offset \( \alpha = \theta_E^{n-1} \theta^{2-n} \).
- Surface density \( \Sigma(r_\perp) \propto r_\perp^{1-n} \).
- Convergence \(\kappa_E = (3-n)/2 \).

For each pair of images
- Lens equation$$ \theta_1 - \alpha_1 = \theta_2 - \alpha_2 $$
- $$ \theta_E^{n-1} = \frac{\theta_1+\theta_2}{\theta_1^{2-n} + \theta_2^{2-n}} $$
- With \(>2\) images, the problem is over constrained.
\(\theta_1\)
\(\theta_2\)
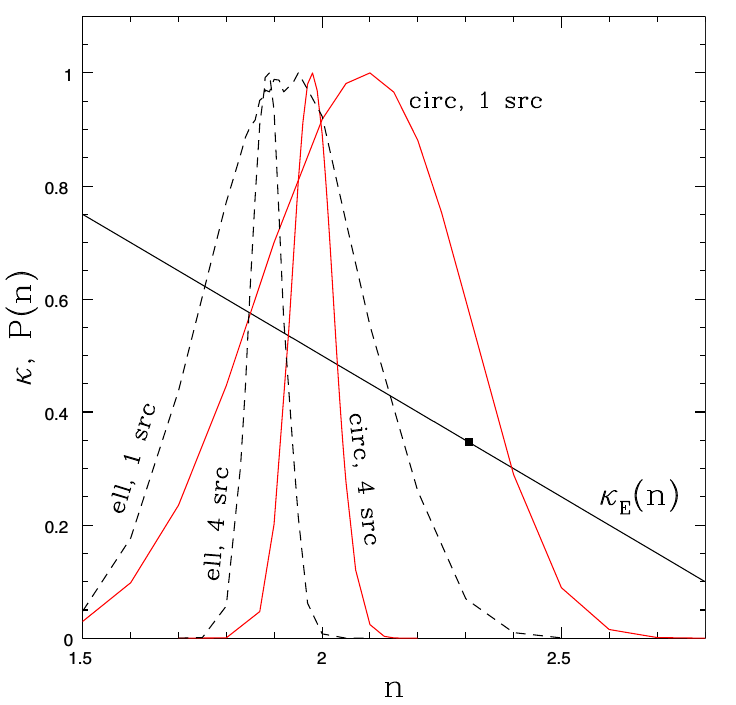
Simulations
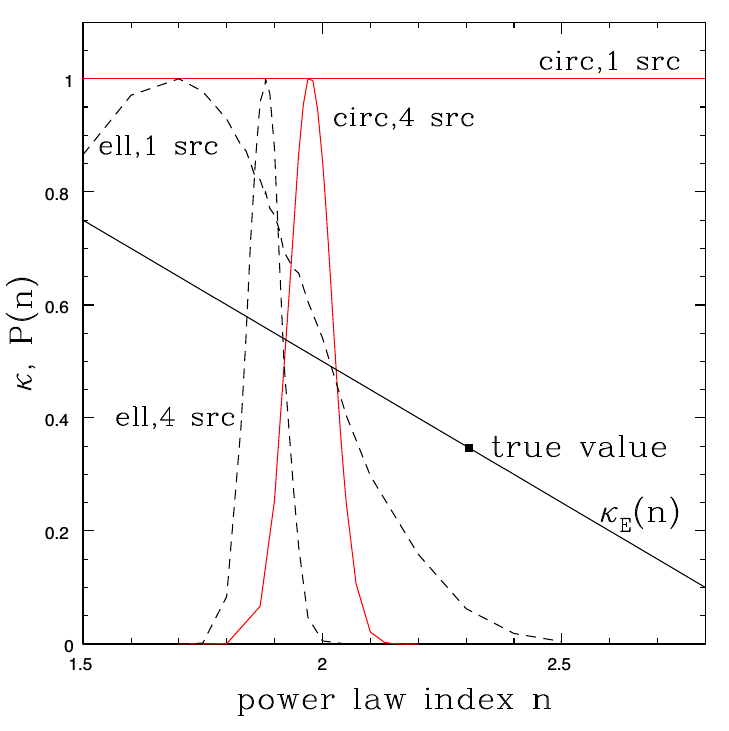
Lensing data alone
Lensing data & kinematics (10% uncertainty)
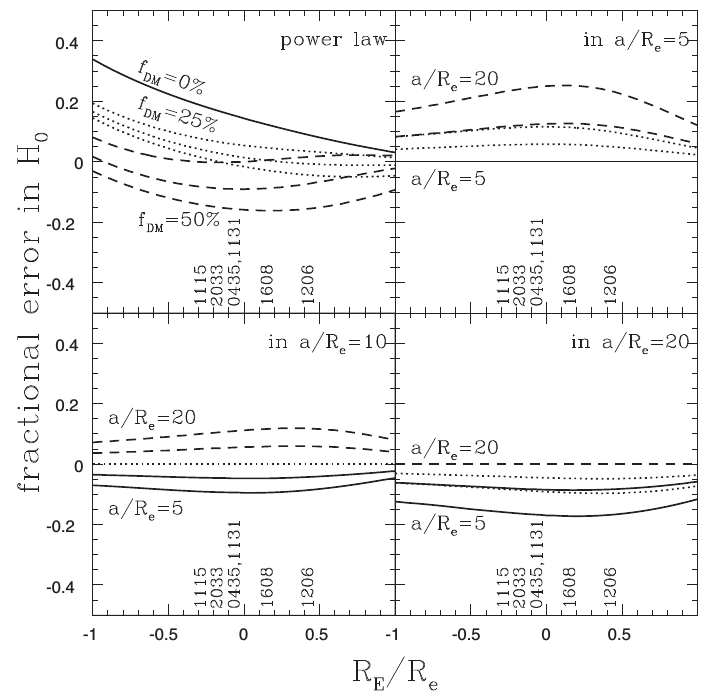
Simulations
No less than ~10% uncertainty on \(H_0\). Adding more lenses does not reduce the uncertainty.
Summary

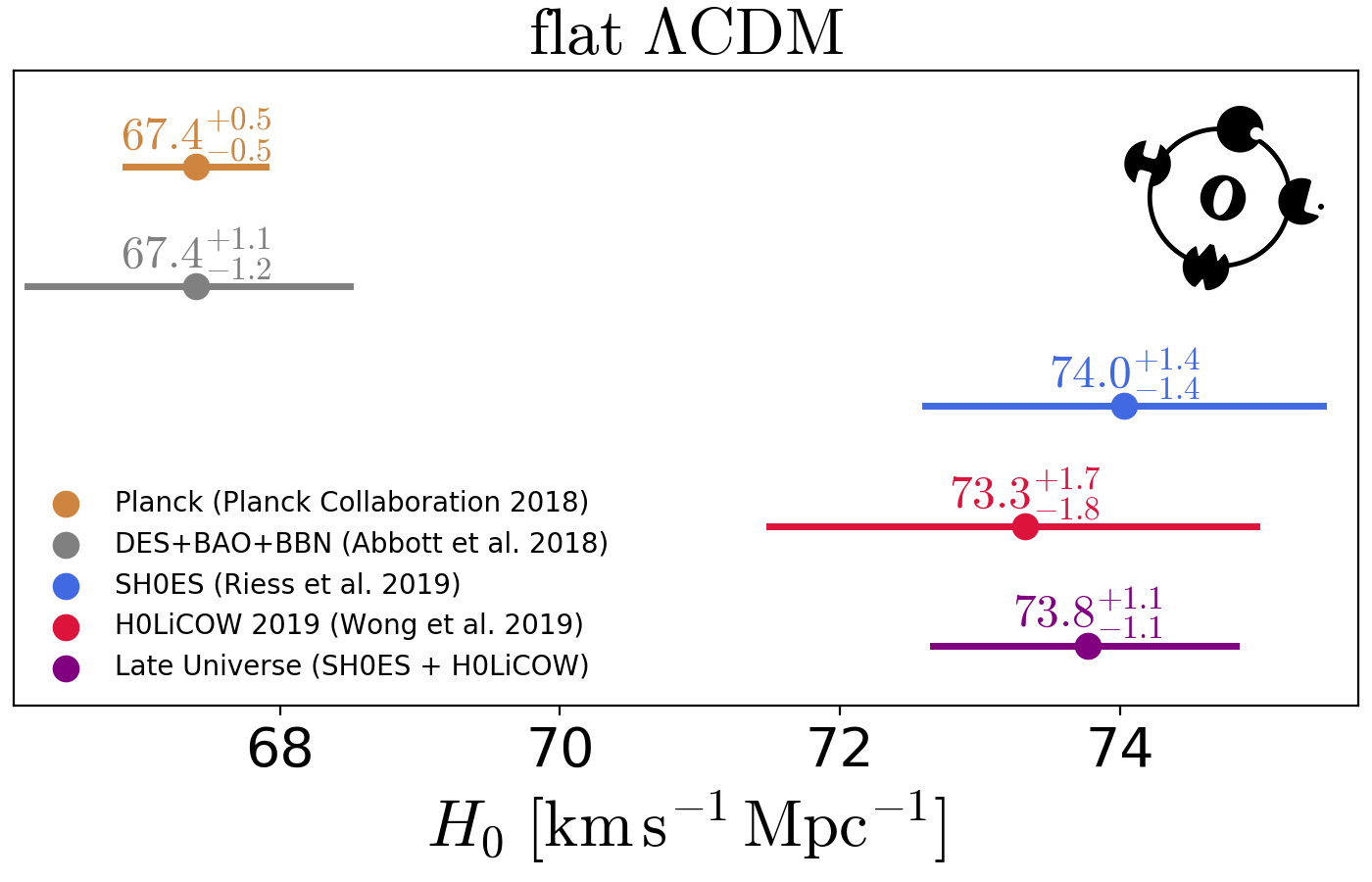
- H0LiCOW reported a 2.4% \(H_0\) measurement.
- Combining lensing information and lens galaxy kinematics, in order to break the \(H_0-\kappa\) degeneracy.
- Kochanek (2020) argues the lens model is overly simplified, leading to very precise and inaccurate \(H_0\).
- Kochanek (2020): "It is unlikely that any current estimates of \(H_0\) from gravitational lens time delays are more accurate than ∼10 per cent, regardless of the reported precision."
- Measuring the time derivative of the time delay? (e.g., Wucknitz et al. 2020)