行星动力学
二体问题分析和简单应用
祝伟
清华大学天文系
2020年9月28日

Mercury
Venus
《行星动力学》课程介绍
- 授课对象:研究生和高年级本科生(理论力学、数理方法)
-
课程内容:
- 用天体力学方法分析行星系统或其他动力学多体(small N-body)系统的演化
- 可独立成一门课,也可与现有《星系动力学》(large N-body)课程合并形成一门更全面的《动力学》课程
- 参考教材:Solar System Dynamics (SSD) by Murray & Dermott
- 本节课为该课程第二讲(第一讲介绍太阳系和行星动力学研究背景)

《行星动力学》第二讲
二体问题分析和简单应用
- 二体问题的重要性
- 二体问题的运动学描述(本节重点)
- 二体问题的动力学描述
- 简单应用
(1.1)二体问题
- 混沌的三(多)体问题
- 二体问题是复杂多体系统的基础
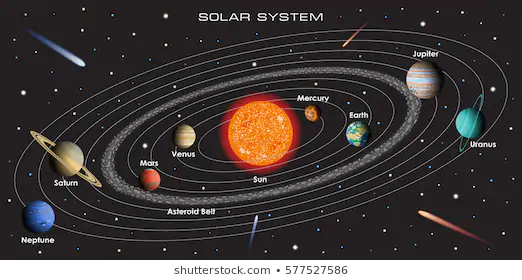
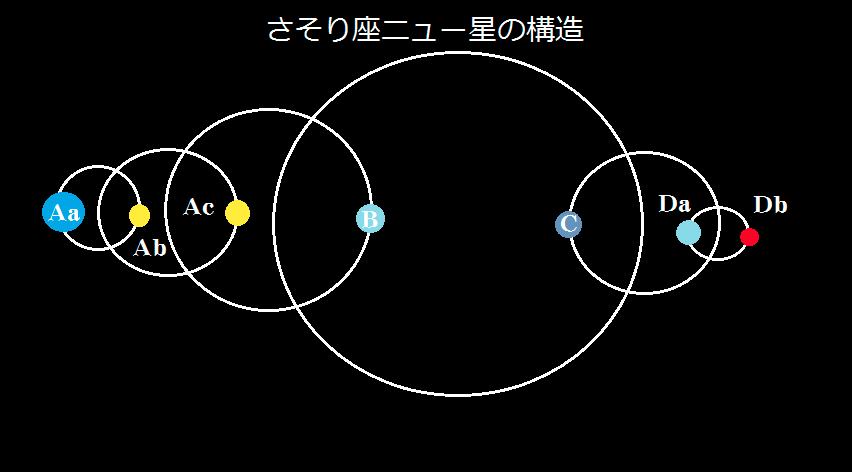
天蝎座\(\nu\):七星系统
等级系统(Hierarchical system)
受限多体系统(restricted system)
(1.2)经验规律:开普勒三定律

Johannes Kepler
(1571–1630)
“第一位天体物理学家,也是最后一位用科学方法研究占星术的人。”
——卡尔·萨根

- 椭圆定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点。
- 等面积定律:在相等时间内,太阳和运动着的行星的连线所扫过的面积都是相等的。
- 周期定律:各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。
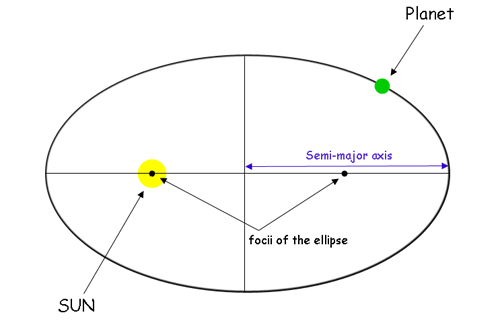
(1.3)二体问题设定
\(O\)
\(\vec{r}_1\)
\(\vec{r}_2\)
\(\vec{r}\)
\(\vec{F}_1\)
\(\vec{F}_2\)
\(m_1\)
\(m_2\)
- 力学方程: $$\red{ \ddot{\vec{r}}_1 = \frac{Gm_2}{r^3}\vec{r} }, \quad \red{ \ddot{\vec{r}}_2 = -\frac{Gm_1}{r^3}\vec{r} }$$ 其中\(G=6.67\times10^{-11}{\rm\,N\,m^2\,kg^{-2}}\)是万有引力常数。
- 相对运动 \(\vec{r}=\vec{r}_2-\vec{r}_1 \longrightarrow\) $$\red{ \ddot{\vec{r}} + \frac{GM}{r^3}\vec{r} = 0 },\quad M\equiv m_1+m_2 $$
- 极坐标 \((r,~\theta)\):$$ \vec{r} = r\hat{r}~,\quad \dot{\hat{r}} = r\dot{\theta} \hat{\theta}~,\quad \dot{\hat{\theta}} = -\dot{\theta} \hat{r} $$
- 角动量守恒:$$ \vec{L} \equiv \vec{r} \times \dot{\vec{r}} = L \hat{z},\quad \red{L=r^2 \dot{\theta}} $$ \( \longrightarrow \) 运动轨迹处于同一平面。
- 运动轨迹方程(详见SSD §2.3) $$\red{ \ddot{r} - r\dot{\theta}^2 = - \frac{GM}{r^2} }$$
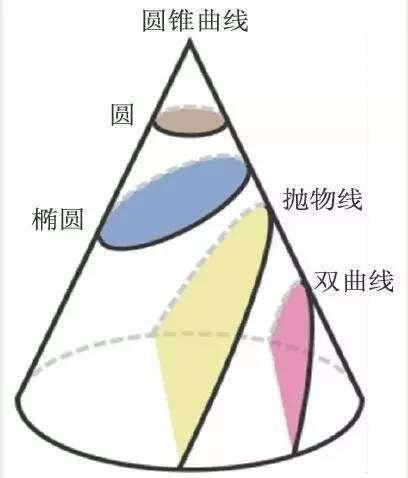
| 离心率 e | 太阳系天体 | |
|---|---|---|
| (椭)圆 | [0, 1) | 行星,小行星 |
| 抛物线 | 1 | 彗星 |
| 双曲线 | >1 | 星际天体 |

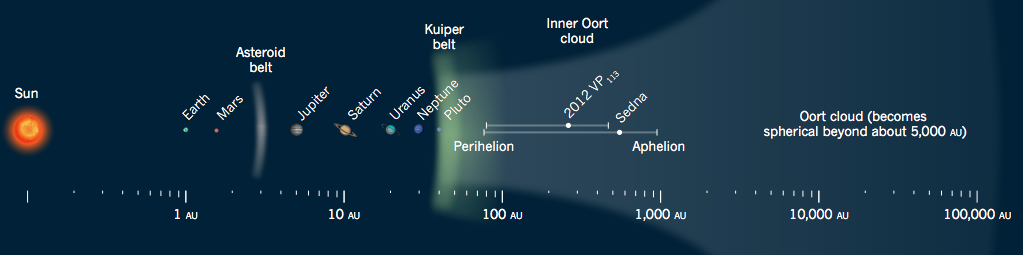
- 圆锥曲线
柯伊伯带
奥尔特星云
(1.4)太阳系天体轨道
Mercury
Venus
(1.5)星际天体


奥陌陌('Oumuamua):\(e=1.2\),2017年发现
鲍里索夫彗星(Comet Borisov):\(e\approx 3.4\),2019年发现
【课堂互动】已知地球绕太阳运转的速度是30千米/秒,如果天文学家观测到位于地球轨道附近的星际天体,那么这个天体相对太阳的速度至少是
(A)17千米/秒
(B)30千米/秒
(C)42千米/秒
(D)60千米/秒
本节总结
- 二体问题的重要性
- 运动学描述(本节重点)
(2.1)椭圆性质
主轴
参考方向
(观测者视线方向)
\(\omega\)
\(f\)
近心点
远心点
- 椭圆的极坐标表示 $$\red{ r = \frac{a(1-e^2)}{1+e\cos{f}} }$$
- 半长轴 \(a\)
- 离心率 \(e\)
- 近心点距离 \(q=a(1-e)\)
- 远心点距离 \(Q=a(1+e)\)
- 近心点幅角 \(\omega\)
- 真近点角 \(f = \theta-\omega\)
- 考虑到 \(q\leq r \leq Q\),引入偏近点角 \(\red{\mathcal{E}}\) $$\red{ r = a(1-e \cos{\mathcal{E}}) }$$
\(\mathcal{E}\)
\(ae\)
\(a\)
几何中心
焦点
$$ r = \frac{L^2}{GM} \frac{1}{1+e\cos{f}}\quad {\rm vs.}\quad r =\frac{a(1-e^2)}{1+e\cos{f}} $$
- 角动量 \( \red{ L^2 =r^2\dot{f}= GM a(1-e^2) }\)
- 周期 $$ P = \int dt = \int df/\dot{f} = L^{-1} \int r^2 df \longrightarrow \red{ P = 2\pi \sqrt{\frac{a^3}{GM}} } $$
- 总能量 $$ E = \frac{1}{2} \dot{\vec{r}}^2 - \frac{GM}{r} \longrightarrow \red{ E = -\frac{GM}{2a} }$$
开普勒第二定律
开普勒第三定律
(2.2)椭圆轨道
(2.3)开普勒方程
- 真近点角 \(f\) ,偏近点角 \(\mathcal{E}\)
$$ r=\frac{a(1-e^2)}{1+e\cos{f}} \quad \& \quad r = a(1-e\cos{\mathcal{E}}) \longrightarrow \cos{f} = \frac{\cos{\mathcal{E}}-e}{1-e\cos{\mathcal{E}}}$$
- 根据 $$ \dot{r}^2 = a^2 e^2 \sin^2\mathcal{E} \dot{\mathcal{E}}^2 = \left(\frac{dr}{df} \dot{f} \right)^2 $$得到微分方程 $$ (1-e \cos{\mathcal{E}}) \dot{\mathcal{E}} = \sqrt{\frac{GM}{a^3}} = \frac{2\pi}{P} $$
- 开普勒方程(Kepler's equation)$$\red{ \mathcal{E}-e\sin{\mathcal{E}} = \frac{2\pi}{P} (t-t_{\rm peri}) \equiv \mathcal{M} ~({\rm 平近点角})}$$
- 开普勒方程的级数展开(详见SSD §2.5)和数值解法(课后习题)
- 开普勒轨道参数:
- 椭圆的形状——半长轴 \(a\),离心率 \(e\);
- 椭圆的指向——近心点幅角 \(\omega\);
- 行星在时刻 \(t\)的位置——真近点角 \(f\) ,偏近点角 \(\mathcal{E}\),或平近点角 \(\mathcal{M}\);
- 轨道平面在三维空间的方位——轨道倾角 \(i\),升交点经度 \(\Omega\)。
\(\omega\)
\(f\)
参考方向
(观测者视线方向)
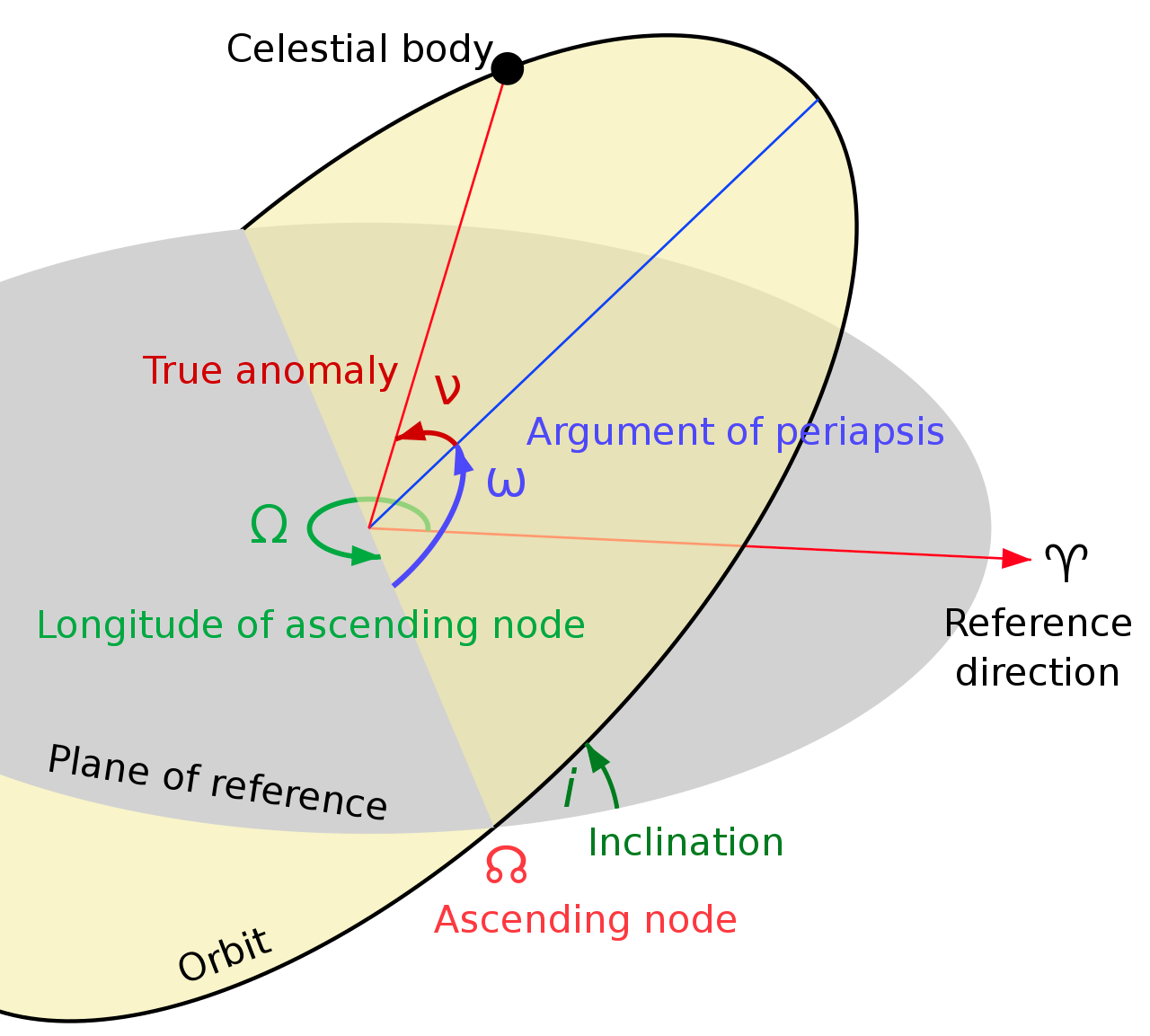
\(f\)
(2.4)确定行星的位置
本节总结
- 二体问题的重要性
- 运动学描述(本节重点)
- 椭圆轨道,开普勒方程,开普勒轨道参数
- 动力学描述
(3.1)知识回顾
- 哈密顿力学
- 哈密顿量 \(H\)
- 正则坐标: 广义动量 \(\vec{p}\),广义坐标 \(\vec{q}\)
- 哈密顿方程 $$ \dot{\vec{q}} = \frac{\partial H}{\partial \vec{p}}, \quad \dot{\vec{p}} = - \frac{\partial H}{\partial \vec{q}} $$
- 德劳奈变量(Delaunay variables)
- (广义坐标)角度:$$\red{({\rm 平近点角~}\mathcal{M},~ {\rm 近心点幅角~}\omega,~ {\rm 升交点经度~}\Omega )}$$
- (广义动量)作用量:$$\red{( \mathcal{L}\equiv\sqrt{GMa},~ \mathcal{G}\equiv\sqrt{GMa(1-e^2)},~ \mathcal{H}\equiv \sqrt{GMa(1-e^2)} \cos{i} )}$$
- 哈密顿量
$$ H_{\rm Kep} = -\frac{GM}{2a} = - \frac{G^2M^2}{2\red{\mathcal{L}}^2} $$
- 哈密顿正则方程
$$ \dot{\mathcal{M}} = \frac{\partial H_{\rm Kep}}{\partial \mathcal{L}} = \frac{G^2M^2}{\mathcal{L}^3} $$
- 带入
$$ \mathcal{M} = \frac{2\pi}{P} (t-t_{\rm peri}), \quad \mathcal{L} = \sqrt{GMa} $$
- 开普勒第三定律
$$ \frac{2\pi}{P} = \sqrt{\frac{GM}{a^3}} $$
(3.2)哈密顿力学研究牛顿二体问题
(3.3)哈密顿力学研究相对论二体问题
- 广义相对论修正的势能 $$ \Phi = - \frac{GM}{r\red{-r_s}} \approx -\frac{GM}{r} \red{- \frac{GMr_s}{r^2}} $$ 史瓦西半径 \( r_s=\frac{2GM}{c^2} \)
- 修正后的哈密顿量 $$ H = -\frac{GM}{2a} \red{- \frac{GMr_s}{a^2} \langle \frac{a^2}{r^2} \rangle} = H_{\rm Kep} \red{+ \Delta H_{\rm GR}} $$ 修正项$$ \Delta H_{\rm GR} = -\frac{2G^2M^2}{a^2c^2} \frac{1}{\sqrt{1-e^2}} = - \frac{2G^{5/2}M^{5/2}}{a^{3/2}c^2} \frac{1}{\red{\mathcal{G}}}$$
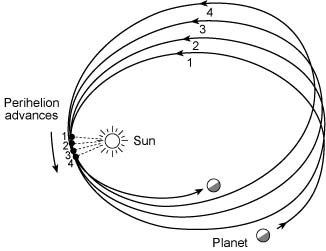
- 近日点进动 $$ \dot{\omega} = \frac{\partial H}{\partial \mathcal{G}} = \frac{2G^{3/2}M^{3/2}}{a^{5/2} c^2 (1-e^2)} $$

- 史瓦西进动
$$ \dot{\omega}_{\rm GR} = \frac{\red{3}G^{3/2}M^{3/2}}{a^{5/2} c^2 (1-e^2)} $$
-
“火神星” (Vulcan)乌龙事件

(3.3)示例:相对论效应的水星进动
- 哈密顿量 $$ H = H_{\rm Kep} + \red{\red\rm 其他天体对该行星的作用} $$
- 合适假设 & 合适参数
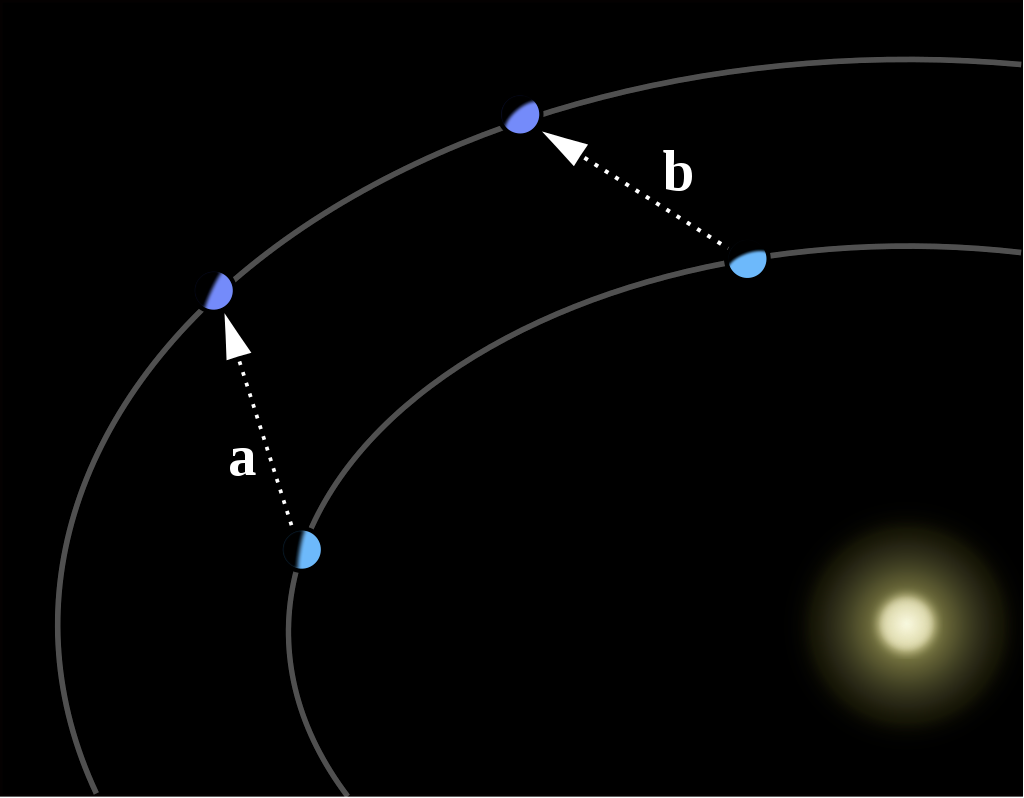
(3.4)行星运动的动力学描述
【课堂互动】以下哪一颗天体对水星进动的贡献最大?
(A)金星(\(0.8\,M_\oplus\)@0.7 AU)
(B)地球(\(1\,M_\oplus\)@1 AU)
(C)木星(\(318\,M_\oplus\)@5.2 AU)
(D)土星(\(95\,M_\oplus\)@9.6 AU)
本节总结
- 二体问题的重要性
- 运动学描述(本节重点)
- 椭圆轨道,开普勒方程,开普勒轨道参数
- 动力学描述
- 哈密顿力学和德劳奈变量,示例(二体问题、水星进动)
- 简单应用
(4.1)海王星的发现
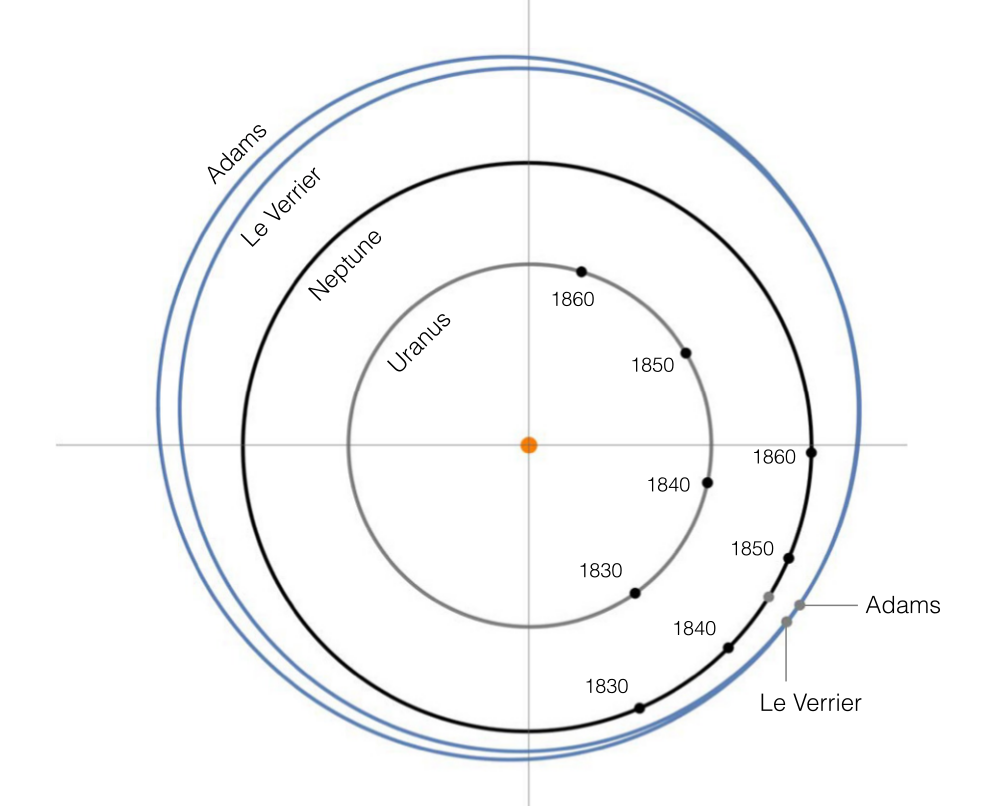
- 1781年,天王星(Uranus)被发现;
- 1846年,法国Le Verrier和英国Adams分别独立预测了未知行星的轨道;同年海王星(Neptune)被发现。

John Couch Adams

Urbain Le Verrier

Johann Galle

Neptune in 1989 as imaged by the Voyager 2 probe
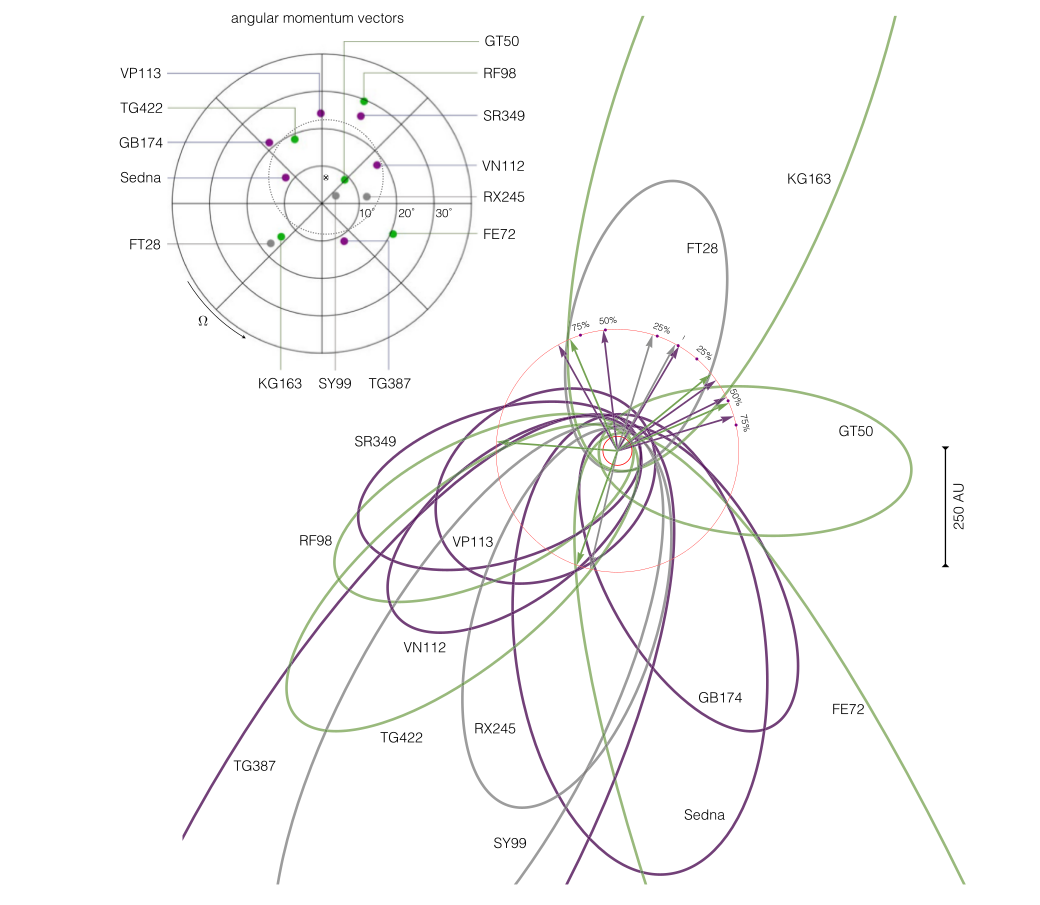
稳定轨道
不稳定轨道
暂稳轨道
- 拥有稳定轨道的遥远柯伊伯带天体(KBO):
- 轨道平面相近(\(\Omega\)相似);
- 近日点相近(\(\omega\)相似);
Batygin et al. (2019)
(4.2)第九大行星假说

Mike Brown (Caltech)
Kanstantin Batygin (Caltech)
- 轨道半长轴:400-800天文单位
- 公转周期:10000-20000年
- 行星质量:5-10倍地球质量
- 轨道离心率:0.2-0.5
(4.2)第九大行星假说
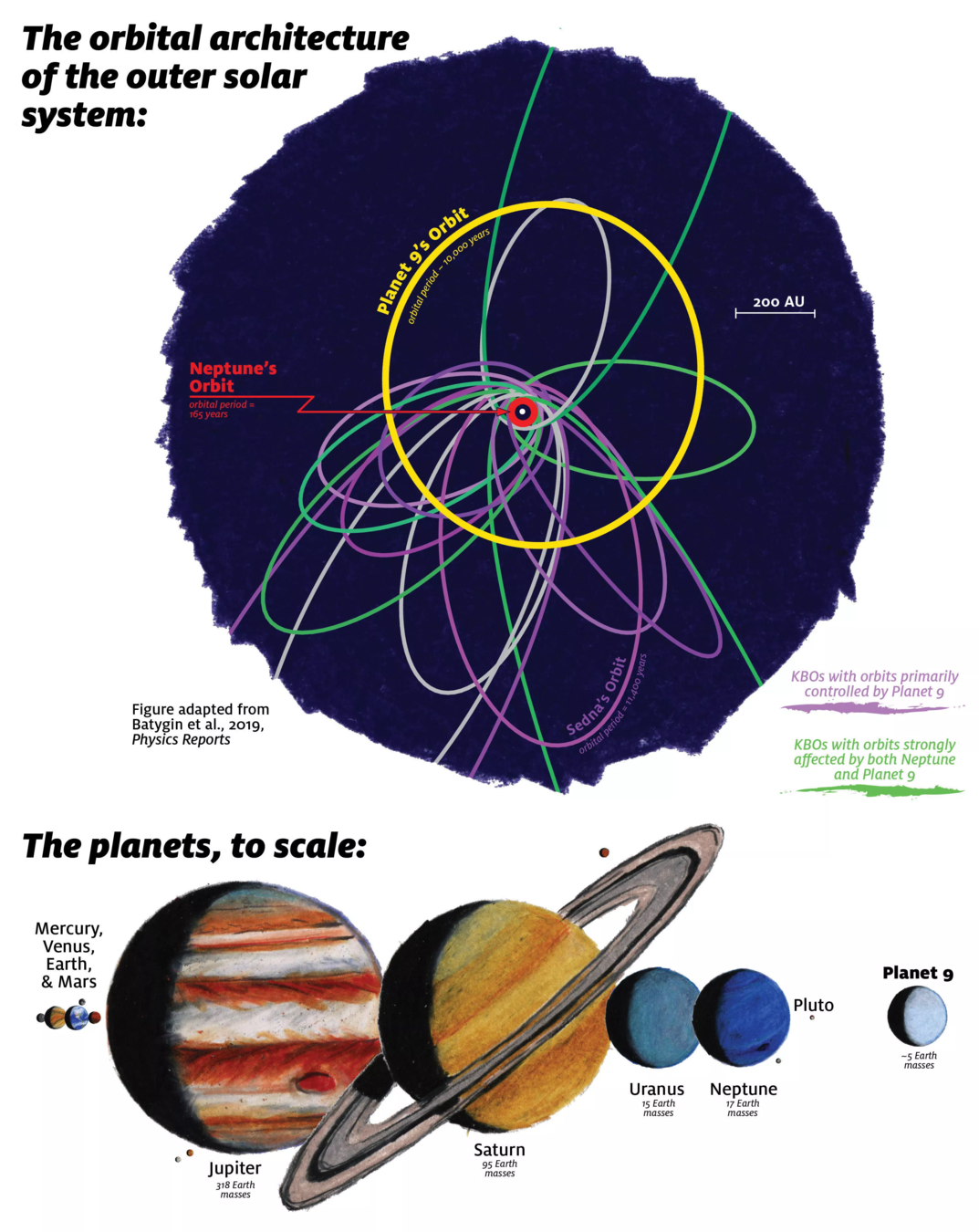
Image credit: James Tuttle Keane/Caltech

RA=6h
赤经RA=12h
RA=0h
RA=18h
发生轨道聚集的KBO近日点位置



春分
夏至
秋分
冬至
第九大行星假说的相关研究涉及行星动力学、天文观测、统计分析等多个方面。
(4.2)第九大行星假说:观测样本偏差?
本节总结
- 二体问题的重要性
- 运动学描述(本节重点)
- 椭圆轨道,开普勒方程,开普勒轨道参数
- 动力学描述
- 哈密顿力学和德劳奈变量,示例(二体问题、水星进动)
- 简单应用
- 海王星的发现,第九大行星假说
(1)天文中的多体系统


天体数目\(n\)
2
~10

天蝎座\(\nu\)
昴星团

- 行星-卫星系统及潮汐现象
- 多行星系统
- 多恒星系统
- 恒星星团
- 星系
- 星系团
动力学多体系统(small N-body)
统计学多体系统(large N-body)
银河系