排序、搜尋
INDEX
- 時間複雜度
- 各種排序法
- 搜尋
時間複雜度
時間複雜度
對於一個程式
要如何計算運行時間
假如今天老師出作業 給你兩種方案:
1. 每天算 10 題乘法
2. 第一天算 1 題加法,第二天算 2 題加法,第三天算 3 題加法……
你會選哪一種?
時間複雜度
假設算一題加法需要 5 秒,算一題乘法需要 20 秒
到了第n天:
1. 10 * n * 20 = (200n)秒
2. (n + 1) * n/2 * 5 =
1. 每天算 10 題乘法
2. 第一天算 1 題加法,第二天算 2 題加法,第三天算 3 題加法……
如果n很小 那2會比較輕鬆 比如等於3 (600>30)
但如果n很大 365的話呢
方案2需要的操作"量級"比較多
所以就長期來說 做方案1會比較輕鬆
量級?
今天如果有兩個函數 f(n) g(n)
當他們接近無限大 來比較他們的大小
超級比一比:
量級?
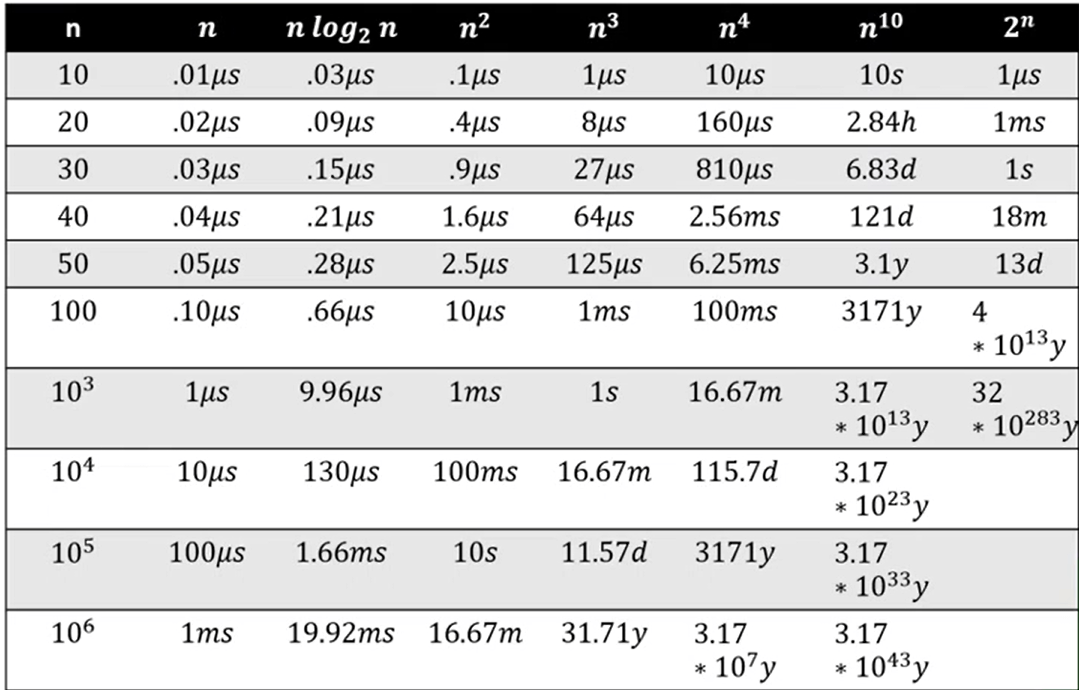
可以看到數字變大 次方比常數影響得多
複雜度的概念
接著來看次數的量級(複雜度)
並評估時間
• 加減乘除
• 取餘數
• 位運算
• 存取記憶體
• 判斷運算子
• 賦值運算子
...
然後把操作的次數算出來
比如長這樣:
大歐符號 (Big-O)
每次要列式子很麻煩
常數其實相對沒那麼重要
最常用的Big-O就出現了!
寫法:
f(n)是複雜度量級的上界
通常會選最接近的上界
(不嚴格<=)
一般會用的就Big-O
其他就聽聽就行
小歐符號 (Little-o)
記為 𝑜(𝑓(𝑛))
其中 𝑓(𝑛) 為複雜度量級的嚴格上界
(嚴格<=)
(不嚴格>=)
Little-omega
Big-omega
記為 Ω(𝑓(𝑛))
其中 𝑓(𝑛) 為複雜度量級的下界
記為 ω(𝑓(𝑛))
其中 𝑓(𝑛) 為複雜度量級的嚴格下界
(嚴格>=)
其中 𝑓(𝑛) 為複雜度量級的嚴格上下界 (完全相同!)
Big-theta
記為 Θ(𝑓(𝑛))
之後演算法的課程一定會一直提到時間複雜度
只是一點點小小的數學
希望不要燒機
各種排序法
各種排序法
氣泡排序 (Bubble Sort)
選擇排序 (Selection Sort)
插入排序 (Insertion Sort)
快速排序 (Quick Sort)
合併排序 (Merge Sort)
接下來會預設為由小排到大
1. 氣泡排序 (Bubble Sort)
重複掃過陣列
比較相鄰元素
如果前>後
交換兩元素
有點像泡泡浮起來的過程
時間複雜度O(n²)
實作code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 20005
int arr[maxn],n;
void bubble_sort(){
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1;j++){
if(arr[j]>arr[j+1])swap(arr[j],arr[j+1]);
}
}
}
signed main(){
while(cin>>n){
for(int i=0;i<n;i++){
cin>>arr[i];
}
bubble_sort();
for(int i=0;i<n;i++){
cout<<arr[i]<<' ';
}
cout<<'\n';
}
}
2. 選擇排序 (Selection Sort)
重複掃過迴圈
找最小值
丟到左邊
時間複雜度O(n²)
實作code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 20005
int arr[maxn],n;
void selection_sort(){
for(int i=0;i<n-1;i++){
int mnindex=i;
for(int j=i+1;j<n;j++){
if(arr[j]<arr[mnindex])mnindex=j;
}
swap(arr[i],arr[mnindex]);
}
}
main(){
while(cin>>n){
for(int i=0;i<n;i++){
cin>>arr[i];
}
selection_sort();
for(int i=0;i<n;i++){
cout<<arr[i]<<' ';
}
cout<<'\n';
}
}
3. 插入排序 (Insertion Sort)
將陣列分成兩堆 已排序/未排序
每次將未排序的插入已排序的正確位置
時間複雜度O(n²)
實作code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 20005
int arr[maxn],n;
void insertion_sort(){
for (int i=1; i<n;i++) {
int key = arr[i];
int j=i-1;
while (key<arr[j] && j>=0) {
arr[j+1]=arr[j];
j--;
}
arr[j+1]=key;
}
}
main(){
while(cin>>n){
for(int i=0;i<n;i++){
cin>>arr[i];
}
insertion_sort();
for(int i=0;i<n;i++){
cout<<arr[i]<<' ';
}
cout<<'\n';
}
}
4. 快速排序 (Quick Sort)
分治概念
選定一個pivot(軸心)
將比pivot小的丟左邊大的丟右邊
時間複雜度不穩定
平均:O(n log n)
最差:O(n²)
不斷切割陣列 直到每個值都到了正確位置
利用遞迴
4. 快速排序 (Quick Sort)
在選擇pivot上
有各種不同寫法
code是選最右邊一位
不同選法會導致複雜度發生改變
使用random可以讓分割比較平均
想想看甚麼情況會讓時間複雜度變成O(n²)
實作code
// C++ Program to demonstrate how to implement the quick
// sort algorithm
#include <bits/stdc++.h>
using namespace std;
int partition(vector<int> &vec, int low, int high) {
// Selecting last element as the pivot
int pivot = vec[high];
// Index of elemment just before the last element
// It is used for swapping
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than or
// equal to pivot
if (vec[j] <= pivot) {
i++;
swap(vec[i], vec[j]);
}
}
// Put pivot to its position
swap(vec[i + 1], vec[high]);
// Return the point of partition
return (i + 1);
}
void quickSort(vector<int> &vec, int low, int high) {
// Base case: This part will be executed till the starting
// index low is lesser than the ending index high
if (low < high) {
// pi is Partitioning Index, arr[p] is now at
// right place
int pi = partition(vec, low, high);
// Separately sort elements before and after the
// Partition Index pi
quickSort(vec, low, pi - 1);
quickSort(vec, pi + 1, high);
}
}
int main() {
vector<int> vec = {10, 7, 8, 9, 1, 5};
int n = vec.size();
// Calling quicksort for the vector vec
quickSort(vec, 0, n - 1);
for (auto i : vec) {
cout << i << " ";
}
return 0;
}還沒教到分治遞迴
但概念大概看一下
5. 合併排序 (Merge Sort)
分治概念
把問題拆分成小問題
時間複雜度O(n log n)
不斷切割陣列 每次合併時將陣列排好
5. 合併排序 (Merge Sort)
分:每次對半切
治:將兩陣列合併 依照順序
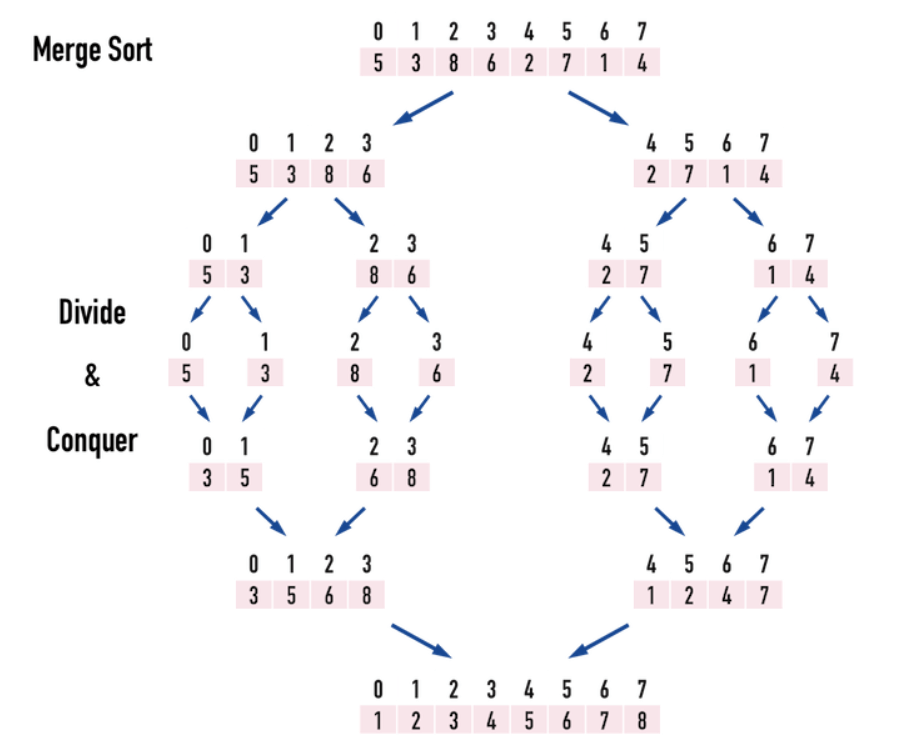
實作code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 1000005
int arr[maxn],n;
void mergesort(int l,int r){
if(l==r)return;
int mid=(l+r)/2;
mergesort(l,mid);
mergesort(mid+1,r);
int n1=mid-l+1,n2=r-mid;
int L[n1+1],R[n2+1];
for(int i=0;i<n1;i++)L[i]=arr[l+i];
for(int i=0;i<n2;i++)R[i]=arr[mid+i+1];
int x=0,y=0,z=l;
while(x<n1 && y<n2){
if(L[x]<R[y]){
arr[z++]=L[x++];
}
else arr[z++]=R[y++];
}
while(x<n1)arr[z++]=L[x++];
while(y<n2)arr[z++]=R[y++];
}
main(){
int n;
while(cin>>n){
for(int i=0;i<n;i++)cin>>arr[i];
mergesort(0,n-1);
for(int i=0;i<n;i++)cout<<arr[i]<<' ';
}
}
還沒教到分治遞迴
但概念大概看一下
補充
補充
題目
如果你想實作看看
檢驗自己的程式對不對
搜尋
搜尋
在資料中找尋特定元素或滿足條件的位置
常見方法:暴力搜、雙指針、二分搜、圖搜尋
使用時機就看題目給的條件
以及資料的特性
並注意複雜度會不會爆
1.暴力搜尋法
又稱線性搜尋法(Linear Search)
時間複雜度O(n)
適用於資料量小、未排序
用for或while迴圈
從頭掃過陣列
如果找到就輸出 沒找到就回傳false或-1
這種簡單東西不太會出現在競程
只要會迴圈就寫得出來
2.二分搜尋法
時間複雜度O(log n)
適用於有單調性的資料
類似終極密碼的玩法
每次將陣列切一半
所以複雜度快很多
比賽常用
實作上有些需要注意的地方
容易搞混
單調性
現在要找一個元素
成立:true
不成立:false
擁有單調性的資料會長怎樣
000000111111111
我們要找的答案就會是在01交界的值
111111000000
或
單調性
舉例
今天要找一個數字:5
擁有單調性的資料會長怎樣
0 0 0 1 1 1 1 1 1 1
這樣就可以一次把左邊或右邊的值全部刪掉
true為>=5的
1 2 3 5 7 9 11 13 15 17
所以如果選到一個值
1:右邊都是true
0:左邊都是false
常見使用時機
找某個值
找滿足條件最大最小值
->一般經典二分搜
->對答案二分搜
實作
有很多流派:
左閉右開、左閉右閉、左開右開...
二分搜常常發生邊界問題
今天講最常見的
左閉右開
左閉右閉
先來講開閉區間是什麼
區間
開區間:不包含左界 不包含右界
(a,b)={x∈R:a<x<b}
半開區間
左開右閉:不包含左界 包含右界
(a,b]={x∈R:a<x≤b}
閉區間:包含左界 包含右界
[a,b]={x∈R:a≤x≤b}
左閉右開:包含左界 不包含右界
[a,b)={x∈R:a≤x<b}
左閉右開
如果要查大小為n的陣列arr
存不存在q
表示方法:[0,n) -> 0,1,...,n-1
每次mid=(l+r)/2
當arr[mid]>q
代表 q在arr[mid]的左邊
當arr[mid]<=q
代表q在arr[mid]的右邊
左閉右開
code
int l=0;
int r=n;
int ans=-1;
while(l<r){
int mid=(l+r)/2;
if(arr[mid]>q)r=mid;
else if(arr[mid]<q)l=mid+1;
else{
ans=mid;
break;
}
}[0,r)
l==r
[l,l)沒意義
小畫家解釋
我建議可以直接背下來
左閉右閉
比較少用
int l=0;
int r=n-1;
int ans=-1;
while(l<=r){
int mid=(l+r)/2;
if(arr[mid]>q)r=mid-1;
else if(arr[mid]<q)l=mid+1;
else{
ans=mid;
break;
}
}[0,r-1]
l==r
[l,l]包含l
小畫家解釋
函式
C++有幫你寫好的函式
lower_bound/upper_bound
lower_bound(a,b,c):
回傳在 a 位置(包含)到 b 位置(不含)之間第一個大於等於 c 的元素的位置。
upper_bound(a,b,c):
回傳在 a 位置(包含)到 b 位置(不含)之間第一個大於 c 的元素的位置。
注意事項
如果沒找到符合條件的值
回傳b
只有在從小到大的陣列才可以使用
底層是用binary search
用*取值
vector<int>v={3,5,1,2};
int main(){
sort(v.begin(), v.end());
cout << *lower_bound(v.begin(), v.end(), 3) << '\n'; // 3
cout << *lower_bound(v.begin(), v.end(), 2) << '\n'; // 2
cout << *upper_bound(v.begin(), v.end(), 3) << '\n'; // 5
cout << *lower_bound(v.begin(), v.end(), 6) << '\n'; // 超出範圍 值不定
}實作時間
模板題
進階題目
想法:
對答案二分搜
會發現答案會有單調性
3.雙指針
常用於:
兩數相加(已排序陣列)
子序列(陣列只往前不回頭)
滑動區間(需要O(n))
維護兩個index
並讓他們在資料中移動
兩數和
前提:已排序陣列
今天要來找兩數和為x的index
舉例 要找總和為8的
1 2 4 5 7
l設為左界、r設為右界
如果總和>8 右界往左
如果總和<8左界往右
兩數和
Code
int i = 0, j = n - 1;
while(i < j){
int sum = a[i] + a[j];
if(sum == target){
cout << i << " " << j;
break;
}
else if(sum < target) i++;
else j--;
}
子序列
前提:子序列 只需要順序相同
給A、B兩字串
判斷B是否為A的子序列
舉例
A : abcde
B : ace
i設為A的第一個index、r設為B的第一個index
每次比對到一樣的j就往後走
子序列
Code
int i = 0, j = 0;
while(i < A.size() && j < B.size()){
if(A[i] == B[j]) j++;
i++;
}
cout << (j == B.size() ? "YES" : "NO");
題目
先教到這裡
希望各位沒燒機