Data Science 101

Linear and logistic regression

Outline

  1. Linear Regression
  2. In practice
  3. Logistic Regression
    1. Model
    2. Cost and optimisation
  4. Multi-classification

Linear regression

Last week


Our first supervised model with the hypothesis:

\( h(x) = \theta_0 + \theta_1 x \)

We have a function ("cost function") to evaluate this model error:



And an algorithm to minimize this function in order to get the best parameters \( \theta_0, \theta_1 \):

Repeat until convergence {


}

J(\theta_0, \theta_1) = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (h(x_i) - y_i)^2
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)

Before

Size Price
1060 244
920 231
250 76
... ...
h(x) = \theta_0 + \theta_1 x

Reality

Size # of bedrooms # of floors Age of home ... Price
1060 5 2 40 ... 244
920 3 1 32 ... 231
750 4 2 15 ... 197
... ... ... ... ... ...

\( x \) (features)

\( y \) (target)

Reality

Size # of bedrooms # of floors Age of home Price
1060 5 2 40 244
920 3 1 32 231
750 4 2 15 197
... ... ... ... ...

Notation:

  \( n \) = Number of training examples

  \( m \) = Number of features

  \( x \) = Matrice "input" variable / features

 \( x_i \) = \( i^{th} \) column of x

  \( y \) = "output" variable / "target" variable

Training set: \( n \times m \) matrix

Hypothesis

h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_m x_m

For convenience of notation, define \( x_0 = 1 \):

h(x) = \theta^T x
J(\theta) = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (h(x_i) - y_i)^2

Cost function & Gradient descent

\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)

Repeat until convergence {


}

In pratice

First steps in feature engineering

Feature Scaling: Idea

 

Make sure features are on a similar scale

Size # bedrooms
1060 2
920 4
250 1

Example:

\( x_1 \): size (0-1000)

\( x_2 \): # of bedrooms (1- 4)

 

Variation of \( \theta_2 \) will impact a lot the value of \( J(\theta) \) compared to \( \theta_1 \)

 

=> We want to put everything at better scale (ie. between some interval)

Rescaling

 

Simpliest method, rescale to the range [0, 1]:

 

 

 

x' = \frac{x - min(x)}{max(x) - min(x)}
Size
1060
920
250
Size'
1
0.83
0

Mean normalization

 

 

 

 

x' = \frac{x - \bar{x}}{max(x) - min(x)}
Size
1060
920
250
Size'
0.39
0.22
-0.62

Standardization

 

Remove the mean and unit variance

 

 

x' = \frac{x - \bar{x}}{\sigma}
std = \sqrt{var} = \sigma = \sqrt{\frac{\displaystyle\sum_{i=1}^{n}(x_i - \bar{x})^2}{n - 1}}

Standardization

 

Remove the mean and unit variance

 

 

x' = \frac{x - \bar{x}}{\sigma}
Size
1060
920
250
Size'
0.89
0.49
-1.39

Polynomial features

Duplicate some feature with their degree

 

Example:

\( \theta_0 + \theta_1 x_1 \)

Second degree: \( \theta_0 + \theta_1 x_1 + \theta_2 x_1^2 \)

Third degree: \( \theta_0 + \theta_1 x_1 + \theta_2 x_1^2 + \theta_3 x_1^3 \)

...

Polynomial features

Logistic regression

Model

Binary classification

 

Email: Spam or not spam?

Tumor: Malignant or benign?

Sport: Will a team win a next game?

 

Output is:

\( y \in \{0,1\} \)

 

0 is the "negative" class

1 is the "positive" class

Intuition

 

Given some data, we want to predict the probability of an output.

 

For example, given the score of a team, what is the probability it will win.

\( 0 < p( win\) | \(score ) < 1 \)

If p(win|score) > 0.5 then predict "Win" ("1") else "Loose" ("0")

 

We want our model to reflect this and outputs in [0,1]

Our example:

Will a team win?

Linear Regression

Sigmoid

g(z) = \frac{1}{1 + e^{-z}}

Sigmoid

g(z) = \frac{1}{1 + e^{-z}}

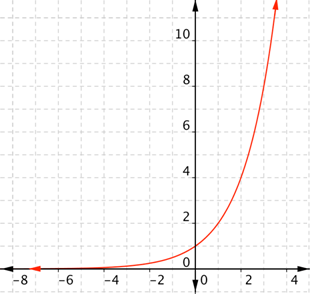
Exponential:

Sigmoid

g(z) = \frac{1}{1 + e^{-z}}

Logistic Regression

 

h(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}

With g = the sigmoid function

h(x) = p(y=1|x;\theta)

"Probability that y = 1, given x, parameterized by \( \theta \)"

Logistic regression

Cost function & optimisation

Loss function in general

J(\theta) = \frac{1}{n} \displaystyle\sum_{i=1}^{n} cost(h(x_i), y_i)
cost(h(x_i), y_i) = (h(x_i) - y_i)^2

For the linear regression, we saw the cost function named "Mean squared error": 

Logarithmic Loss

The loss to a certain predicted probability \( p \) in regard to the truth \( y \)

LogLoss(y, p) = y \space log \space p

Logarithmic Loss

The loss to a certain predicted probability \( p \) in regard to the truth \( y \)

LogLoss(y, p) = y \space log \space p
LogLoss(1, 0.9) = 0.10536

Examples:

LogLoss(1, 0.5) = 0.69315
LogLoss(1, 0.1) = 2.3026

Logarithmic Loss

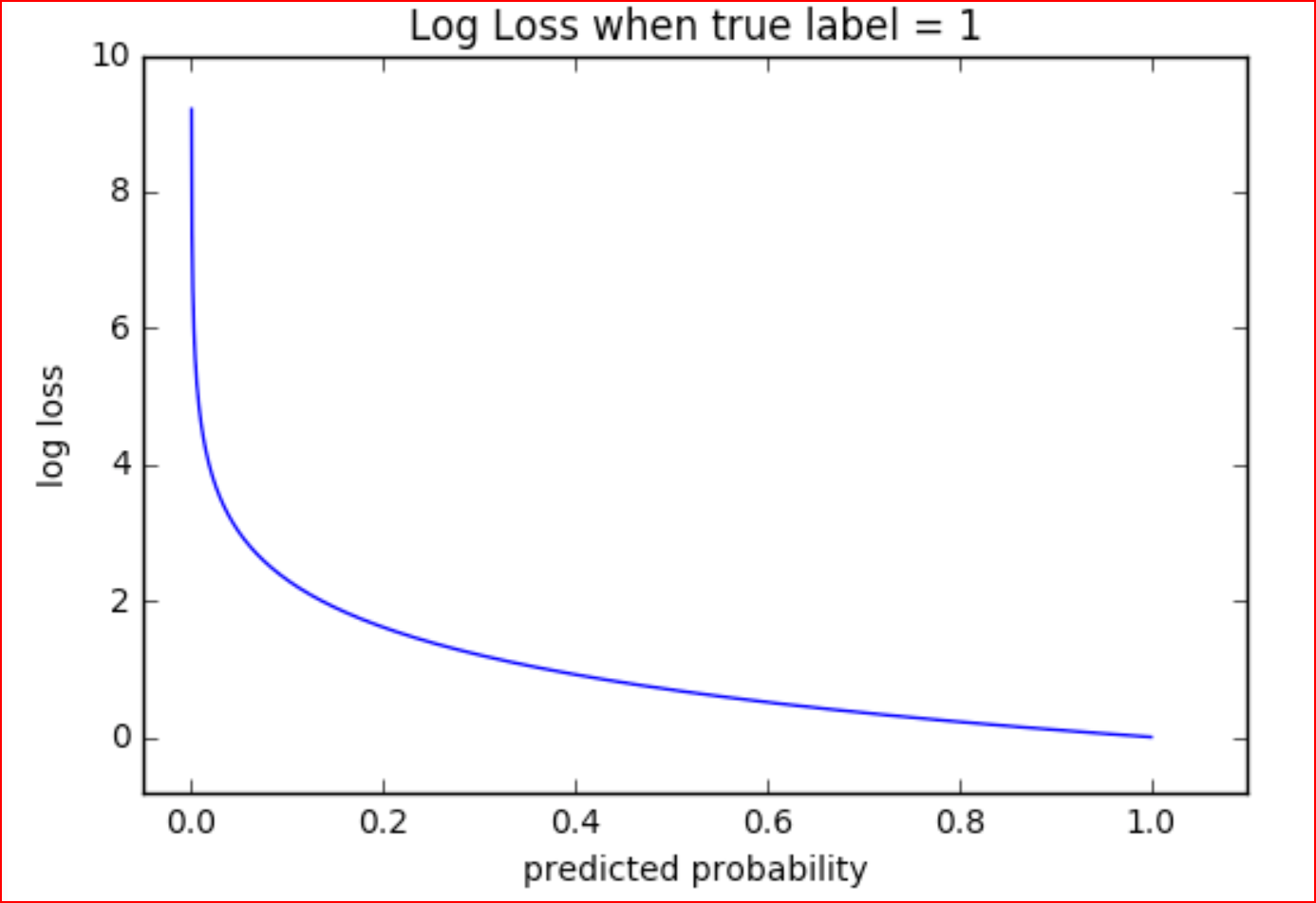
Logarithmic Loss

J(\theta) = - \frac{1}{n} \displaystyle\sum_{i=1}^{n} y_i \space log \space h(x_i) + (1 - y_i) \space log(1 - h(x_i))

0 if the current sample \( i \) has a negative output

\( y = 0 \)

0 if the current sample \( i \) has a positive output

\( y = 1 \)

Gradient Descent

Nothing really change!

Repeat until convergence {

 

}

\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)

Just compute the partial derivative of our new cost function

Multi-classification

One vs All

One vs All

 

For \(K \) classes, \( j = 1 \space ... \space K \)

 

Train multiple classifier \( h_j(x) \) for each class \( j \)

 

 On a new input \( x \), to make a new prediction, pick the class \( j \) that maximes:

$$ \max_{j} h(x) $$

Code

Linear Regression

from sklearn import linear_model

ols = linear_model.LinearRegression()

ols.fit(X, y)       # Train your model
ols.coef_           # Theta
ols.predict(X_new)  # Predict on a new value
from sklearn import linear_model

clf = linear_model.LogisticRegression()

clf.fit(X, y)       # Train your model
clf.coef_           # Theta
clf.predict(X_new)  # Predict on a new value

Logistic Regression

Where are we?

Now

 

You know how to solve a regression and classification model with a linear model.

You also know how to rescale features.

 

What you miss to work on your first problem

Next session, we will learn how to train and evaluate a model properly in practice.

And how to tackle some common problems (overfitting, CV,...)

What's next

 

After that, for supervised learning, it all will be new models, optimisation methods, tricks to tackle specific problems: imbalanced learning, dealing with text data, image data,... 

Internal competition(s) ?

 

Kaggle Inclass

 

Regression: Predict NYC house price

Classification: Predict if a patient has a disease or not

Multi-Classification: Predict if a water pump in Africa is functional, need some repairs or don't work at all

Made with Slides.com