演算法之雜七雜八
Yeedrag
今天會談的東西:
前綴和
差分
位元運算
快速冪
單調隊列
前綴和
模板題:
Q筆詢問,問[a,b]區間和?
(你要用線段樹我也沒意見)
視為前i項的和!
| 1 | 5 | 3 | 7 | 6 |
|---|
| 1 | 6 | 9 | 16 | 22 |
|---|
arr
pre
查詢[a,b]的和: pre[b]-pre[a-1]
二維拓展:
\(pre[x][y] = \sum^{x}_{i=1}\sum^{y}_{j=1} arr[i][j]\)
| 1 | 3 | 7 |
|---|---|---|
| 4 | 2 | 8 |
| 1 | 1 | 5 |
| 1 | 4 | 11 |
|---|---|---|
| 5 | 10 | 25 |
| 6 | 12 | 32 |
arr
pre
sum[a~b][c~d] = pre[b][d] - pre[a-1][d] - pre[b][c-1] + pre[a-1][c-1]
如果帶修改?
k筆要求,在第c格加val?
差分
模板題:
Q筆要求,每次把[a,b]加上c,
最後問位置k之值為何?
提示:怎麼設計前綴和來做到要的結果呢?
思路:
[a,b]區間要加c,那只要在a加上c,並且
在b+1減掉c,全部做前綴和就可以了!
| c | 0 | 0 | -c | 0 |
|---|
arr
| c | c | c | 0 | 0 |
|---|
pre
在[1,3]加上c的例子
位元運算
如其名,是對位元做運算的東西
位元?
電腦儲存的單位,為二進位,意思是只有0或是1
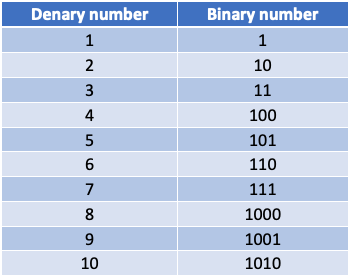
優點:
位元運算通常都超級快
缺點:
可讀性低/優先順序低(要記得括號)
左移/右移
把所有的位元往左/右移動,
最左/右的位元消失和補0
0010 = 2
左移: 0100 = 4 (數字乘二)
右移: 0001 = 1 (數字除二)
<</>>
#include<bits/stdc++.h>
#define debug(x) cerr<<#x<<" = "<<(x)<<endl;
using namespace std;
int main(){
int k = 1<<2;//左移兩次
cout<<k<<endl;//4
int v = 13>>1//右移一次
cout<<v<<endl;//6
}AND運算
&
把兩個變數的對應位元進行AND邏輯運算
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<(5&3)<<endl;//1
cout<<(7&4)<<endl;//4
}0101 (5)
0011 (3)
&=
0001 (1)
0111 (7)
0100 (4)
&=
0100 (4)
OR運算
|
把兩個變數的對應位元進行OR邏輯運算
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
bruh他歪七扭八ㄉ
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<(5|3)<<endl;//7
cout<<(7|4)<<endl;//7
}0101 (5)
0011 (3)
|=
0111 (7)
0111 (7)
0100 (4)
|=
0111 (7)
XOR運算
^
把兩個變數的對應位元進行XOR邏輯運算
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<(5^3)<<endl;//6
cout<<(7^4)<<endl;//3
}0101 (5)
0011 (3)
^=
0110 (6)
0111 (7)
0100 (4)
^=
0011 (3)
NOT運算
~
顛倒所有的位元
~0 = 1
~1 = 0
常用位元技巧:
n>>1/n<<1 乘除二(的次方)
(n&1) == 1 判斷奇數
n&-n 最低位的位元1 (之後會用到)
位元枚舉
bitset (這算位元技巧嗎.w.)
思考問題:
給你\(n\)個數字(\(n\)為奇數),裡面除了一個數字只出現一次以外,其他的都會出現兩次,請在\(O(N)\)內找出那一個數字
提示點我
a ^ a = 0
非常好文章們:
練習:
btw codeforces超愛考位元ㄉ
這題好玩
快速冪
如何計算 \(a^n\) ?
#include<bits/stdc++.h>
using namespace std;
int pow(int a,int n){
int sum = 1;
for(int i=0;i<n;i++) sum*=a;
return sum;
}
int main(){
cout<<pow(3,5)<<endl;//243
}複雜度: \(O(N)\)
能不能更快?

根據指數運算我們可以知道:
\(a^{b+c} = a^b * a^c\)
\(a^{2b} = a^b * a^b = (a^b)^2\)
\(a^0 = 1\)
所以可以發現:
\(a^n = a^{\frac{n}{2}}*a^{\frac{n}{2}} \)
(如果\(n\)是奇數要多乘\(a\))
所以我們只需要\(logn\)次計算就可以算出\(a^n\)了!
實際拆解:
\(3^1 = 3^0 * 3^0 * 3 = 3\)
\(3^3 = 3^1 * 3^1 * 3 = 27\)
\(3^6 = 3^3 * 3^3 = 729\)
\(3^{13}\) = \(3^6 * 3^6 * 3\ = 1594323\)
計算\(3^{13}\):
In code:
#include<bits/stdc++.h>
using namespace std;
long long fastpow(int a,int n){
if(n==0) return 1;//a^0 = 1
int half = fastpow(a,n/2);//算出 a^(b/2)
if(n&1){//n是奇數
return half*half*a;
} else {
return half*half;
}
}
int main(){
cout<<fastpow(3,15)<<endl;//14348907
}當然也可以寫成迴圈式,而且會快一點點
取模?
\((a*b)\%m = (a\%m) * (b\%m)\)
#include<bits/stdc++.h>
using namespace std;
int mod = (int)1e9+7;
long long fastpow(int a,int n){
if(n==0) return 1;//a^0 = 1
//a%=mod;
int half = fastpow(a,n/2);//算出 a^(b/2)
if(n&1){//n是奇數
return ((half*half)%mod*a)%mod;
} else {
return (half*half)%mod;
}
}
int main(){
cout<<fastpow(3,13)<<endl;//1594323
}\(O(logn)\)算出費式數列第n項?
單調隊列
介紹一個STL:
deque!
deque支援操作:
簡單來說就是前後都可以操作!
push_back/front 添加元素到尾/頭
pop_back/front 移除尾/頭元素
insert 插入元素
erase 移除元素
clear 清空容器
empty 回傳是否是空的
size 回傳目前長度
跟別的stl用法差不多就不放扣了 .w.
模板題:
a416: Sliding Window
給一個數列大小為n,有一個滑窗長度為k會從最左邊開始滑到右邊,詢問每次滑動時當前滑窗裡的最大/小值?
注意這題k有可能大於n
關鍵:只存下以後有可能是答案的值!
以下以找滑窗最大為例(最小也差不多la)
我們想要做一個前面最大、且是單調遞減的隊列
前面彈出條件: 超出隊列
後面彈出條件: 不可能為答案 (新進來的比他還大,以後不可能有機會是他最大)
範例:
| 1 | 3 | -1 | -3 | 5 | 3 | 6 | 7 |
|---|
n = 8, k = 3
隊列(裡面存索引值):
輸出:
i =
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
3
3
5
5
6
7
slides做動畫好難;-;
#include<bits/stdc++.h>
#pragma GCC optimize("O3")
#define guracute ios_base::sync_with_stdio(false); cin.tie(0)
using namespace std;
void solve(){
int n,k;
while(cin>>n>>k){
deque<int> mono_dq;//單調隊列
vector<int> vec(n);//原陣列
for(auto &i:vec) cin>>i;
k = min(n,k);//此題k有可能>n
//最小
for(int i=0;i<n;i++){
//對於最小,保持隊列最前最小
//要注意一定要檢查隊列裡是否有東西不然會RE
while(mono_dq.size()&&mono_dq.front()<=i-k){
//如果目前隊列最前面的已經出滑窗了
mono_dq.pop_front();
}
while(mono_dq.size()&&vec[mono_dq.back()]>vec[i]){
//從後面把不可能的開始刪除
mono_dq.pop_back();
}
mono_dq.push_back(i);//目前數字放入隊列
if(i==k-1) cout<<vec[mono_dq.front()];
//到k-1時才正式包進第一次滑窗
if(i>k-1) cout<<" "<<vec[mono_dq.front()];
}
cout<<endl;
mono_dq.clear();
//最大
for(int i=0;i<n;i++){
while(mono_dq.size()&&mono_dq.front()<=i-k){
mono_dq.pop_front();
}
while(mono_dq.size()&&vec[mono_dq.back()]<vec[i]){
mono_dq.pop_back();
}
mono_dq.push_back(i);
if(i==k-1) cout<<vec[mono_dq.front()];
if(i>k-1) cout<<" "<<vec[mono_dq.front()];
}
cout<<endl;
}
return;
}
signed main(){
guracute;
int cases = 1;
//cin>>cases;
while(cases--) solve();
return 0;
}Code:
練習:
(可以用單調stack)