圖論

Graph Theory

BY:覺得圖論很難的Yeedrag

圖論很難 加油ㄅ

應該說接下來兩堂都很難w

wat is 圖論 owo?

圖論（英語：graph theory），是組合數學分支，和其他數學分支，如群論、矩陣論、拓撲學有著密切關係。圖是圖論的主要研究對象。圖是由若干給定的頂點及連接兩頂點的邊所構成的圖形，這種圖形通常用來描述某些事物之間的某種特定關係。頂點用於代表事物，連接兩頂點的邊則用於表示兩個事物間具有這種關係。嗨我是咩咩

圖論起源於著名的柯尼斯堡七橋問題。該問題於1736年被歐拉解決，因此普遍認為歐拉是圖論的創始人。[1]

Den wat is 圖?

一堆點+一堆線。

嚴格解釋:點的集合加上邊的集合

一些你需要知道的名詞:

點

圖上的一個個點。

邊

圖上的一個個邊。

環

只有第一個和最後一個頂點重複的路徑。

邊的方向性

有些邊，我們可能會限定只能從一側到另一側，而不能雙向通行，我們稱之為有向邊。

點權/邊權

在點/邊上面定義的權重。

3

點度

一個點共連接了幾條邊。

對於有向圖，又會分為:

1.入度 (通往這個點的邊數)

2.出度(離開這個點的邊數)

點與點間的關係

1.相鄰:兩點直接連接

2.連通:兩點間存在路徑

 

A

B

C

(A,B),(B,C)相鄰且連通

(A,C)(A,C)間則只有連通

圖ㄉ分類:

有向圖

有方向的圖

btw,如果是有向無環圖(DAG),

可以做拓撲排序(Topological Sort)喔!

可能下學期還啥的會教.jpg

 

無向圖

沒有方向的圖

連通圖

圖上每個點都與其他點連通

樹

除了根節點外

每個節點都有一個母節點與一或多個子節點

or

邊的數量為\(V-1\)的連通圖

現實的樹

程式的樹

畫成圖後

A

B

C

F

G

H

E

D

根節點

葉節點

父節點

子節點

無情開偷學長動畫爽阿刺阿

一些樹的重要性質

  • 保證無環

  • \(V-1\)個邊

完全圖

任意兩點都相連

*二分圖

可以被切為兩個不相連的點集

水la 名詞解釋好ㄌ

可以開始正課了!  ⁽⁽٩(๑˃̶͈̀ ᗨ ˂̶͈́)۶⁾⁾

How do I 存 the 圖?

  • 相鄰矩陣 

  • 相鄰串列

相鄰矩陣

建一個\(V*V\)的矩陣，

\((i,j)\)項表示\(i\)跟\(j\)是否相鄰(or存邊權)

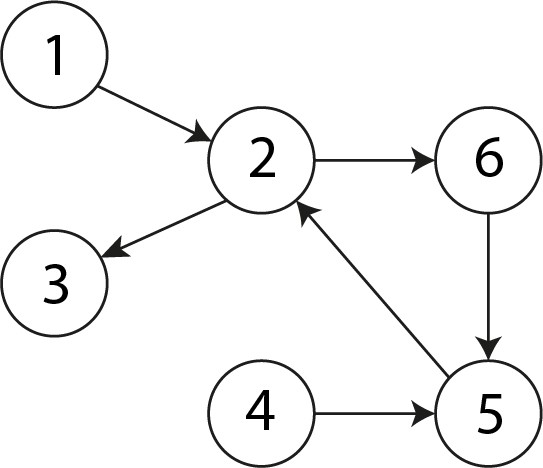
example:

1

2

3

4

5

6

  1   2   3   4    5   6
  1   0   1   1   0   0   1
  2    1   0   0   0   0   0
  3    1   0   0   1   1   0
  4   0   0   1   0   0   0
  5   0   0   1   0   0   0
  6   1   0   0   0   0   0

相鄰串列

開\(V\)個串列

對於第\(i\)個點，存\(i\)點相鄰的邊

example:

      1                1,2,6
      2                  1
      3                1,4,5
      4                  3
      5                  3
      6                  1

1

2

3

4

5

6

Which is better?

空間複雜度:

相鄰矩陣是\(O(V^2)\)

相鄰串列是\(O(V)\)

時間複雜度:

遍歷:

矩陣是\(O(V^2)\)

串列是\(O(V)\)

是否相鄰:

矩陣：\(O(1)\) , 串列：\(O(V)\)

兩種的寫法:

int graph_1[V][V];
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        graph[a][b] = 1;
        //graph[b][a] = 1;
    }
}
vector<int> graph[V];
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        graph[a].push_back(b);
        //graph[b].push_back(a);
    }
}

帶權vector就存pair!

圖的遍歷

BFS/DFS

快速穿插小技巧

遍歷一個陣列，通常我們都是

for(int i=0;i<n;i++){
    arr[i]......
}

可以用

for(auto i:arr){
    // i is every element
    // in the array
}
for(auto &i:arr){
    //如果會更動到arr裡的值
    //i前面要加&!
}

想想看，你玩遊戲時搜索

地牢的時候會用甚麼策略?

深度優先搜尋(DFS)

優先往深的地方一直走!

1

2

3

4

5

6

順序:1->2->3->4->5->6

實作?

一直探到底才回來前面先碰到的....

可以用遞迴(或stack)!

DFS實作

bool visited[V+1];
void dfs(int v){
    visited[v] = true;
    /*
        做想在遍歷時做的事
    */
    for(auto i:graph[v]){
        if(!visited[i.first]){
            dfs(i.first);
            //還沒遇過就dfs下去
        } else {
            continue;
        }
    }
}

廣度優先搜尋(BFS)

有先遇到的就先走!

1

2

3

4

5

6

順序:1->2->3->6->4->5

實作?

先遇到先做...

Queue!

BFS實作

bool visited[V+1];
void bfs(int start){
    queue<int> que;
    que.push(start)//把第一個點push進queue
    visited[start] = true;//已造訪
    while(que.size()){//當還有東西時
        /*
            做你在遍歷時想做的事
        */
        for(auto i:graph[que.front()]){
            if(!visited[i.first]){
            	visited[i.first] = true;
                que.push(i.first);
            }
        }
        que.pop();
    }
}

實作重點們:

一定要記得紀錄是否造訪過，

否則您將吃TLE一枚。

BFS要在推入前就記錄造訪過，

不然遇過的有機會再被推一次

實作練習:

CSES-Message Route

需要紀錄距離的BFS

實作練習:

ZJ-我的領土有多大

BFS的裸題

實作練習:

NEOJ-庭院裡的水池

可以說是遞迴練習的DFS/BFS題目

實作練習:

NEOJ-魔王戰前夜 II - 迷宮探索

要回推移下的題目.w.

 

實作練習:

TIOJ- 走夜路小心遇到鬼，還有女高中生

難度有點高的BFS

 

Made with Slides.com