分治
Divide & Conquer
什麼是分治
分治
- 分:分割問題
- 治:解決問題
分成子問題
- 把問題分割成規模較小的子問題
- 常見的分割方法:分左右
解決子問題
- 有些非常簡單的子問題是已知的
- 遞迴求解
合併子問題
- 善加利用問題的特性
- 找出好的方法從子問題的答案推到大問題的答案
合併排序
Merge Sort
合併排序
- \(給你n個數字,請由小到大排好\)
- \( O(n \log n) \)
- 一種做法是分治
合併排序
1. 分成子問題
把序列分成左右兩半
2. 解決子問題
- 遞迴處理
- 只有一個元素的序列必然是排好的
3. 合併子問題
如果我們已經知道兩個排序好的陣列,怎麼合併成一個排序好的陣列?
1
1
2
3
5
6
6
8
9
好好利用兩邊已經排序好的特性
| 1 | 2 | 3 | 5 | 8 |
|---|
| 1 | 6 | 6 | 9 |
|---|
\(A\)
\(B\)
\(C\)
\(時間複雜度:O(n)\)
\(有 O(\log n)層,每層都是O(n)\)
\(所以就能O(n \log n)排序了!\)
| 1 | 1 | 2 | 3 | 5 | 6 | 6 | 8 | 9 |
|---|
來看看整棵遞迴樹
| 1 | 1 | 2 | 3 |
|---|
| 5 | 6 | 6 | 8 | 9 |
|---|
| 1 | 2 |
|---|
| 1 | 3 |
|---|
| 5 | 8 |
|---|
| 6 | 8 | 9 |
|---|
| 6 | 8 |
|---|
2 2 1 3 5 8 6 8 9
void merge_sort(int a[], int l, int r) { //[l, r)
if (r - l <= 1) return;
int mid = (l + r) / 2;
merge_sort(a, l, mid);
merge_sort(a, mid, r); //thus, [l, mid) and [mid, r) are sorted
int sorted[r - l];
int li = l, ind = 0;
for (int ri = mid;ri < r;ri++) { //two pointers
while (li < mid && a[li] <= a[ri]) {
sorted[ind] = a[li];
ind++, li++;
}
sorted[ind] = a[ri];
ind++;
}
while (li < mid) { //insert remaining elements
sorted[ind] = a[li];
ind++, li++;
}
for (int i = 0;i < r - l;i++) a[i + l] = sorted[i];
}寫寫看
分治的使用時機
分治的使用時機
- 大問題不好解,但小問題可以解
- 可以分割成幾個互不影響的小問題
- 遞迴定義的東西
- 很多資料結構都是用分治的想法
分治其實無所不在
分治經典演算法
- 線段樹
- BIT
- Karatsuba 多項式乘法
- Strassen 矩陣乘法
- FFT
- CDQ分治
- 重心剖分
- 整體二分搜
逆序數對
\(逆序數對:在一個序列A中,若存在 i < j 且\\a_i > a_j ,我們稱(i, j)為一組逆序數對\)
給定一個序列,問有多少組逆序數對
\(n \leq 10^5, a_i \leq 2^{31} - 1\)
直接做
- 枚舉每一個數
- 數他右邊有幾個東西比他小
- \(O(n^2)\)
回顧一下merge sort
- 我們在合併的時候是輪流從兩個陣列取東西
- 有時從前半段陣列取,有時從後半段陣列取
- 當我們從後半段陣列取東西時,代表這個元素比當前在前半段陣列的所有元素都小
- 欸~後面的比較小~逆序數對!
對merge sort 動手腳
- 一樣把陣列分成前後兩半邊遞迴下去
- 遞迴完會回傳這個子區間的逆序數對數
- 合併的時候多紀錄一些東西
- 每次把後半段陣列放進去的時候,紀錄當前前半段陣列剩多少元素
- 這個值代表跨越前後兩半邊的逆序數對數
- 答案=前面+後面+跨越前後
主定理
Master Theorem
主定理
\(如果一個演算法的時間函數T(n)可以表示成:\)
\((1)若f(n) \in O(n^{\log_ba - \epsilon}),則T(n)\in O(n^{\log_ba})\)
\((2)若f(n) \in \Theta(n^{\log_ba}),則T(n)\in \Theta(n^{\log_ba} \log n)\)
\((3)若f(n) \in \Omega(n^{\log_ba + \epsilon}),則T(n)\in \Theta(f(n))\)
主定理
一個可能比較好懂的形式?
\(如果一個演算法的時間函數T(n)可以表示成:\)
\((1)若d < \log_ba ,則T(n)\in O(n^{\log_ba})\)
\((2)若d = \log_ba,則T(n)\in \Theta(n^d \log n)\)
\((3)若d > log_ba,則T(n)\in \Theta(n^d)\)
\(就是d和 \log_ba比大小,一樣大加log,否則取大的\)
舉例
回顧剛剛Merge sort:
每次遞迴我們把問題分成兩個子問題
每個子問題的規模縮小為\(\frac{n}{2}\)
合併的時間複雜度是\(O(n)\)
\(T(n) = 2T(\frac{n}{2}) + O(n)\)
\(\Rightarrow a=2, b=2, d=1\)
\(\because d=1=\log_22=\log_ba\)
\(\therefore T(n) \in \Theta(n \log n)\)
舉例
Strassen矩陣乘法
每次遞迴我們把兩個相乘的矩陣各自分成四個小矩陣
每個子問題的規模縮小為\(\frac{n}{2}\)
但我們只需要進行7次小矩陣乘法即可合併
額外的合併時間複雜度是矩陣加法的\(O(n^2)\)
\(T(n) = 7T(\frac{n}{2}) + O(n^2)\)
\(\Rightarrow a=7, b=2, d=2\)
\(\because d=2<\log_27=\log_ba\)
\(\therefore T(n) \in O(n ^{\log_27})\)
證明
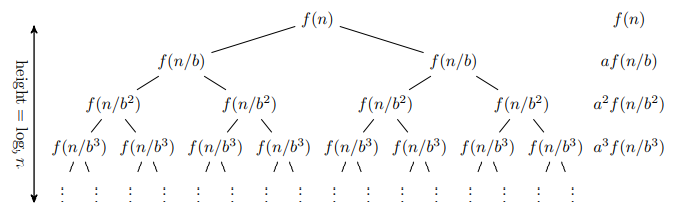
證明主定理
平面最近點對
\(給定平面上n個點的座標(x_i, y_i),\\求出這n個點中最近的兩個點的距離是多少?\)
\(n \leq 50000, x_i, y_i \leq 2^{31} - 1\)
註:這邊的距離指的是歐幾里得距離
平面最近點對
1. 分成子問題
把平面分成左右兩半
2. 解決子問題
- 遞迴處理
- 只剩一個點的半平面上的最近點對距離為0
3. 合併子問題
如果我們已經知道左右兩邊的最近點對距離,怎麼合併出整個平面的最近點對距離?
\(d_1\)
\(d_2\)
假設分成左右兩塊的都算好答案了...
答案會是 min(左, 右, 左右之間)
\(d\)
\(d\)
\(d=min(d_1, d_2)\)
可以注意到:
\(d\)
\(d\)
\(d\)
\(d\)
對於一個點,最多只有8個點在\(y \pm d\)的範圍內
複雜度
\(T(n) = 2T(\frac{n}{2}) + O(n \log n)\)
\(\Rightarrow O(n \log^2 n)\)
快速冪
\(計算a^n\)
直接做?
\(O(n)\)
再快一點~
分治!
\(若n是奇數:a^n=a \times a^{n-1}\)
\(若n是偶數:a^n=a^{\frac{n}{2}} \times a^{\frac{n}{2}}\)
\(T(n) = T(\frac{n}{2}) + O(1)\)
\(\Rightarrow O(\log n)\)
實作
遞迴版
int exp(int a, int b, int m){
if(b==0) return 1;
if(b%2){
return a*exp(a,b-1,m)%m;
} else{
int tmp=exp(a,b/2,m);
return tmp*tmp%m;
}
}實作
迭代版
int exp(int g, int x, int p) {
int r, c = g % p;
for (r = 1; x > 0; x >>= 1) {
if (x & 1) {
r = (r * c) % p;
}
c = (c * c) % p;
}
return r;
}其他練習題
\(構造一種方法用L型方塊鋪滿2^n \times 2^n平面\)
\(n \leq 10 \)
\(構造一個1到N的排列\\滿足這個序列不存在⻑度為 3 的等差子序列\)
\(N \leq 10^5\)
計算\(a \times b\)
(可以先做到subtask 4)
Q1. CF 1311F
直線上有 n < 10^5 個點,第 i 個點有位置pi,依速度 vi 做等速運動,令 d(i, j) 為第 i 個點跟第 j 個點在以後無限時間最短的距離,
求