Shortest Paths
yennnn
最短路徑問題
最短路徑問題
給定一張圖,尋找兩節點之間的最短路徑長
- 有權圖?無權圖?
- 有沒有負權?
- 單點源?全點對?
前提:沒有負環!
無權圖的最短路徑
BFS
vector<int> G[MAXN];
queue<int> que;
int length[MAXN] = { 0 };
bool visited[MAXN];
void bfs(int x){
que.push(x);
visited[x]=1;
while(!que.empty()){
int now=que.front();
que.pop();
for(auto i:G[now]){
if(!visited[i]){
visited[i]=1;
que.push(i);
length[i] = length[now] + 1;
}
}
}
}\( O(V + E)\)
Bellman-Ford Algorithm
鬆弛 Relaxation
假設起點\(O\)到點\(U, V\)的距離分別為\(d_u, d_v\)
如果\(d_u + w_{uv} < d_v \)
就把\(d_v\)更新為\(d_u + w_{uv} \)
Bellman-Ford Algorithm
每次枚舉所有邊進行鬆弛,鬆弛 \( V - 1\) 次
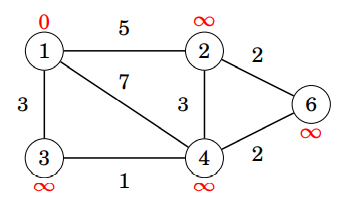
初始化:將所有點的距離設為 \( \infty \)
起點的距離設為\(0\)
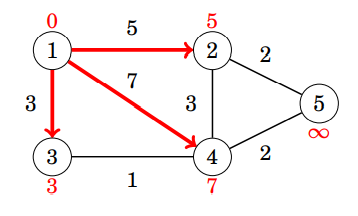
鬆弛第一輪
鬆弛第二輪
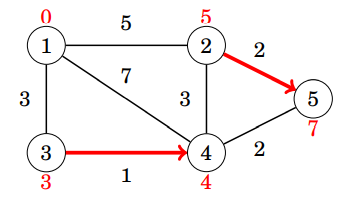
鬆弛第三輪
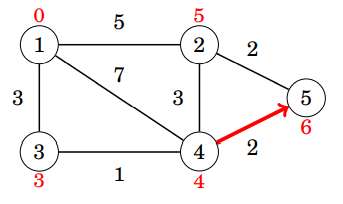
鬆弛第四輪

Bellman-Ford Algorithm
- 鬆弛第\(n\)輪後,可以保證深度\( \leq n\)的路徑最短
- 一張圖最深的路徑深度為\(V - 1\)
- 鬆弛\(V - 1\)輪保證找到所有點的最短路徑
實作
vector<pii> G[MAXN];
int dis[MAXN];
void Bellman_Ford(){
dis[1]=0;
for(int i=2;i<=n;i++) dis[i]=INF;
for(int i=0;i<n-1;i++){
for(int j=0;j<m;j++){
int a = edge[j].F, b = edge[j].S;
if(dis[a]!=INF && dis[a]+w[j]<dis[b]){
dis[b]=dis[a]+w[j];
}
}
}
}複雜度:\( O(VE) \)
優點
- 可以對負權圖操作
- 可以判負環
缺點
複雜度差:\(O(VE)\)
Bellman-Ford Algorithm
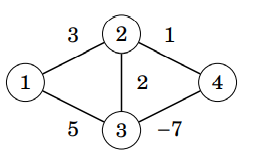
判負環
鬆弛\(V - 1\)輪後,保證所有點的距離都是最短路徑
再鬆弛一輪,如果有點的距離可以更短
就存在負環,反之則否。
無論起點為何都對
優化:SPFA
Shortest Path Faster Algorithm
每次只枚舉有被鬆弛到的點的邊
SPFA
- 維護一個queue
- 初始enqueue起點
- 枚舉queue.front()的所有邊鬆弛
- 當一個點被鬆弛到時,enqueue
- queue空時,搜尋完成
期望複雜度:\( O(V + E)\)
最差複雜度:\( O(VE) \)
SPFA判負環
- 維護每個點enqueue的次數
- 若有點enqueue \( > V \)次,存在負環
Dijkstra's Algorithm
Dijkstra's Algorithm
每次選沒被選過的點中,距離最小的點
枚舉它所有邊鬆弛
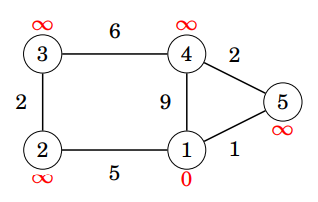
初始化:將所有點的距離設為 \( \infty \)
起點的距離設為\(0\)
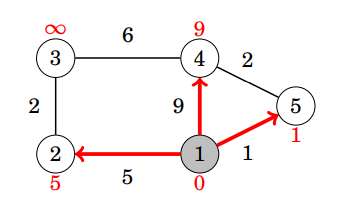
選第一個點
選第二個點
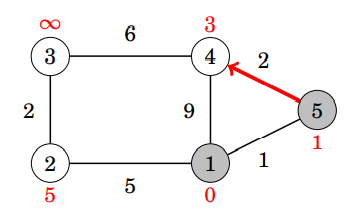
選第三個點
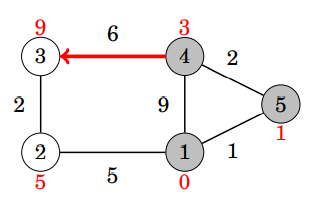
選第四、五個點
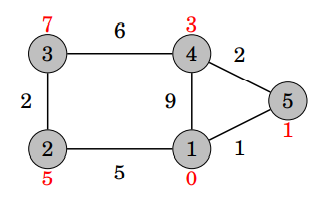
但是當遇到負權時...
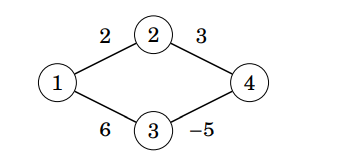
有點太greedy了
實作
for (int i = 1; i <= n; i++) distance[i] = INF;
distance[x] = 0;
q.push({0,x});
while (!q.empty()) {
int a = q.top().second; q.pop();
if (processed[a]) continue;
processed[a] = true;
for (auto u : adj[a]) {
int b = u.first, w = u.second;
if (distance[a]+w < distance[b]) {
distance[b] = distance[a]+w;
q.push({-distance[b],b});
}
}
}用priority queue可在\( \log V\)複雜度插入、刪除、尋找距離最小點
複雜度:\( O((E + V) \log V)\)
優點
複雜度很讚:\( O((E + V) \log V)\)
缺點
只能用在非負權圖
Dijkstra's Algorithm
Floyd-Warshall Algorithm
Floyd-Warshall Algorithm
利用DP,一次解決全點對最短路徑
\(dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])\)
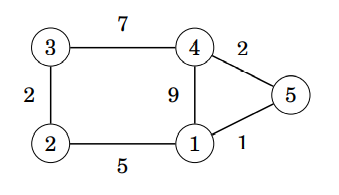
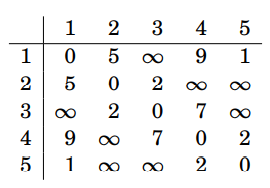
初始化:
\(dp[i][j] = 0 若 i == j\)
\(dp[i][j] = w 若 i, j 相鄰且E(i, j) = w\)
\(dp[i][j] = \infty otherwise\)

枚舉k = 1:
以轉移式
\(dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])\)轉移
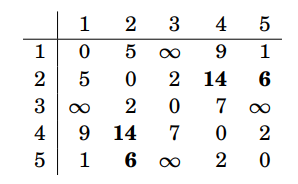

枚舉k = 2:
以轉移式
\(dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])\)轉移
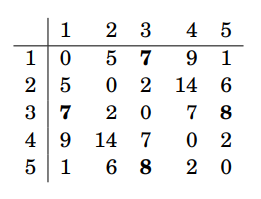

枚舉k = 3:
以轉移式
\(dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])\)轉移
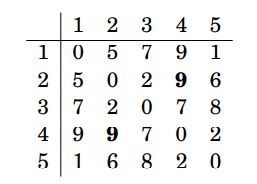

枚舉k = 4, 5:
以轉移式
\(dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])\)轉移
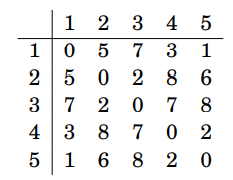
完成後\(dp[i][j] = 點i和點j間的最短路徑長\)
實作
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) dis[i][j] = 0;
else if (adj[i][j]) dis[i][j] = adj[i][j];
else dis[i][j] = INF;
}
}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j]);
}
}
}
短短的扣很好實作
複雜度:\( O(V^3)\)
可處理負權圖