SMPC
综述《Secure Multi-Party Computation:Theory, practice and application》
TOC
- SMPC
- OT
- GC
- HE
SMPC
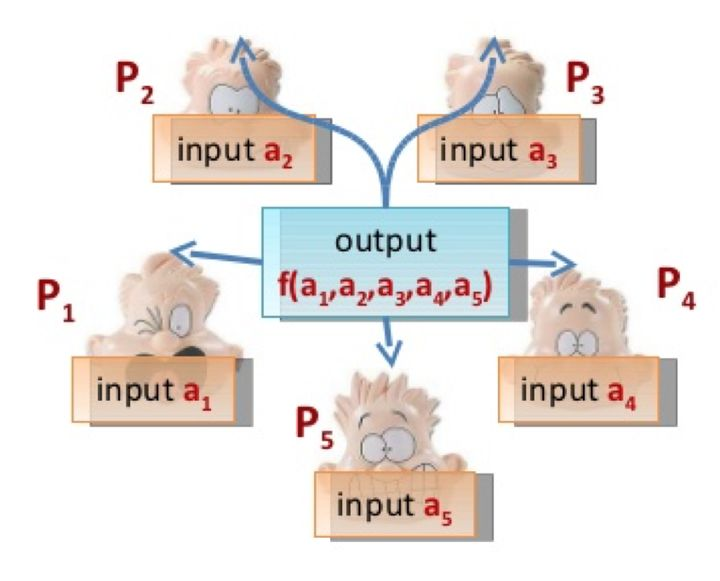
f(x_1, x_2, x_3, \cdots) = (y_1, y_2, y_3, \cdots)
SMPC
f(x_1, x_2, x_3, \cdots) = (y_1, y_2, y_3, \cdots)
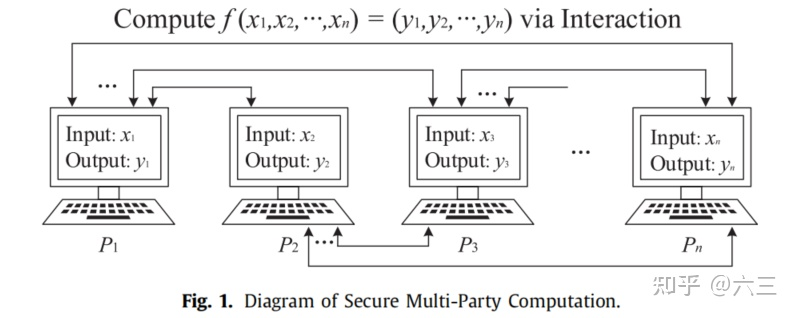
SMPC
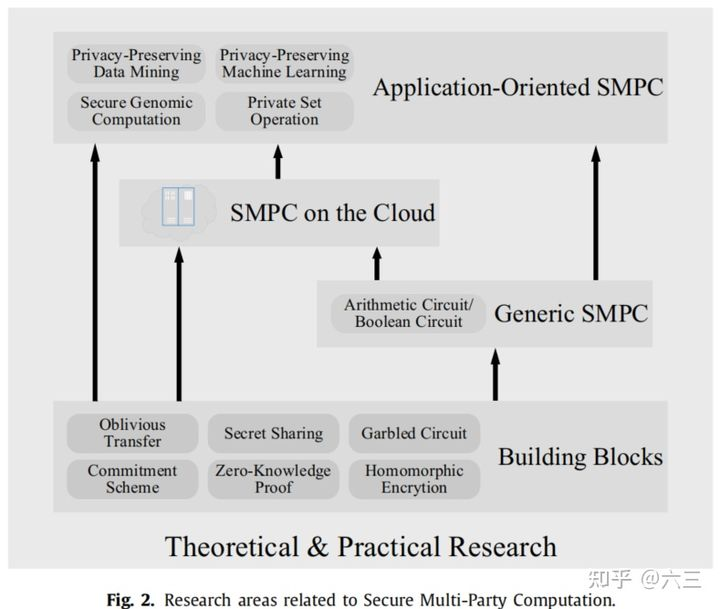
SMPC Security
- 隐私性
- 正确性
- 输入独立性
- 输出保证性
- 公平性
理想/现实模拟范式
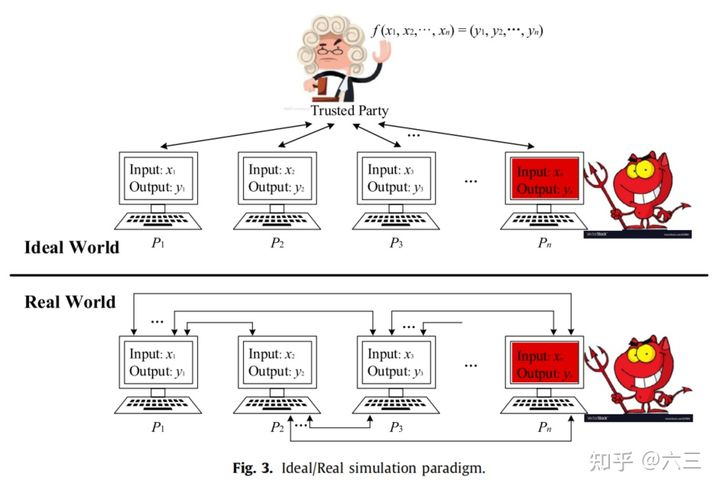
攻击模型
- 半诚实对手模型
- 恶意攻击模型
- 隐蔽的攻击模型
OT 不经意传输
Oblivious Transfer
OT
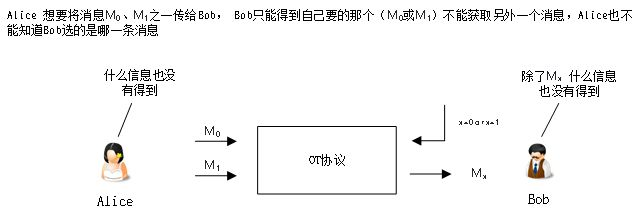
OT

OT
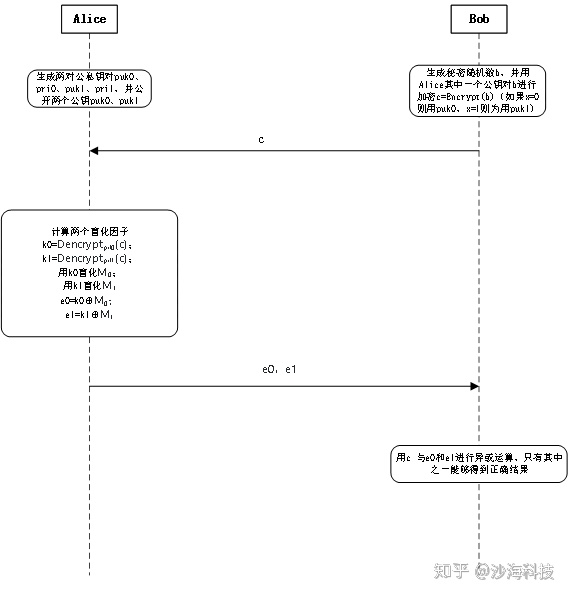
OT
\begin{aligned}
& Alice: v_0, v_1, s, r_0, r_1 \\
& Bob: i \in \{0,1\}, k \\
& Bob \text{ want to get } v_i \\
& \text{Generate } g \in Z_p, g \text{ is large integer}, p \text{ is large prime number}\\\\
1. & Alice \to Bob : g_s \\
2. & Bob \text{ calculate } L_i = \begin{cases} g^k & \text{if }i=0 \\ g^{s-k} & \text{if } i = 1 \end{cases} \\
3. & Bob \to Alice :L_i \\
4. & Alice \text{ calculate } C_0 = (g^{r_0},(L_i)^{r_0}\oplus v_0), C_1=(g^{r_1},(g^s/L_i)^{r_1}\oplus v_1) \\
5. & Alice \to Bob C_0, C_1 \\
6. & Bob \text{ get } v_i = \begin{cases}
C_0[0]^k \oplus C_0[1] = (g^{r_0})^k \oplus (L_i)^{r_0} \oplus v_0 = (g^{r_0})^k \oplus (g^k)^{r_0} \oplus v0 & \text{if }i=0 \\
C_1[0]^k \oplus C_1[1] = (g^{r1})^k \oplus (g^s/L_i)^{r_1} \oplus v_1 = (g^{r_1})^k \oplus (g^k)^{r_1} \oplus v_1 & \text{if } i = 1 \end{cases}
\end{aligned}
GC 混淆电路
Garbled Circuit
GC

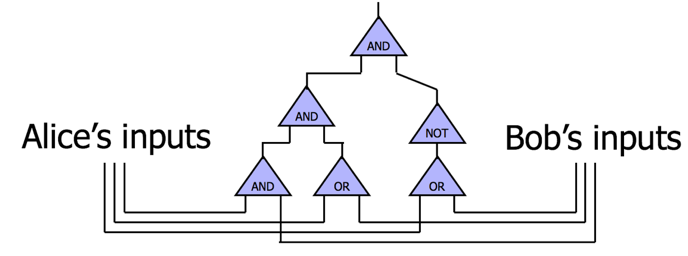
GC

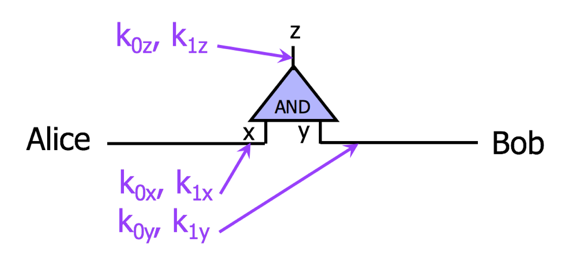
GC


HE 同态加密
Homomorphic Encryption
We skip it
通用安全多方计算
Yao's

LEGO
不同于Lindell和Pinkas在整个电路中采用cut-and-choose技术的方法,Nielsen和Orlandi提出的LEGO方法依赖于为了获得更好的渐近效率而在门级进行的cut-and-choose测试。这个方法要求电路发生器Gen向接收器发送多个与非门。接收者Eval打开这些门的随机子集以进行检查。如果检查成功,Eval将未打开的门随机排列到桶中,表示冗余的与非门。Eval在Gen的帮助下,将每个桶内的门焊接在一起,然后再将桶焊接在一起,形成一个即使每个桶中有少数门故障,也能正确计算出函数的电路。
应用
云辅助的安全多方计算
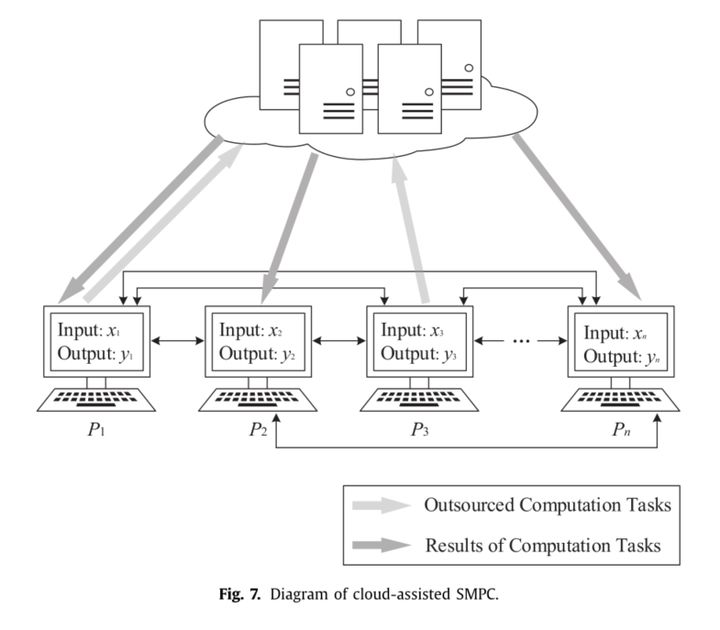
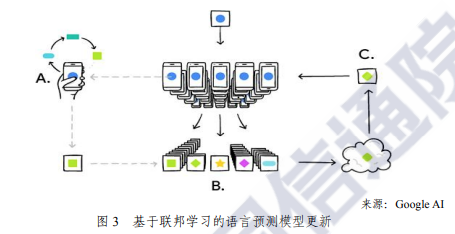
通过SMPC确保机器学习的安全
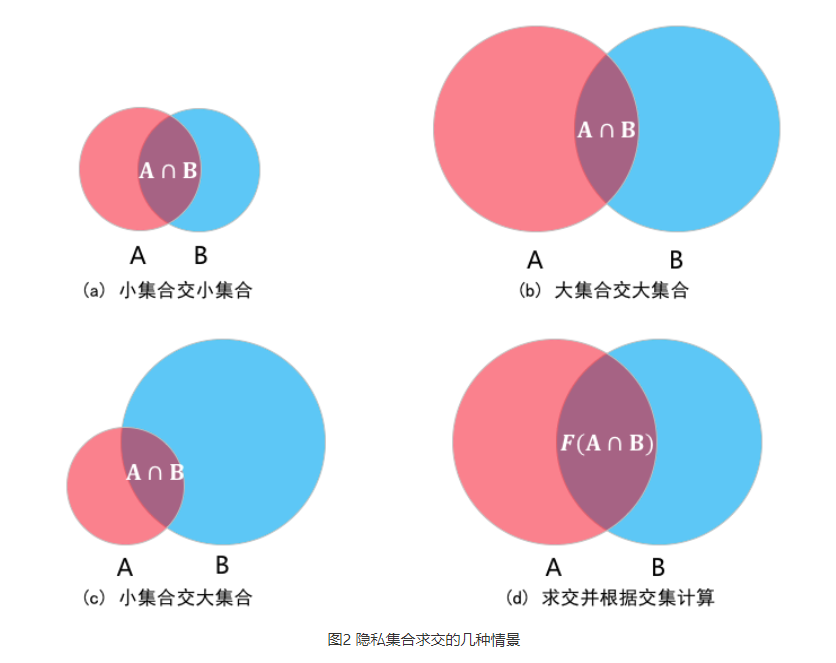
隐私集合计算
安全基因组序列比较