資訊學科能力競賽

複賽題解

猜猜我出哪幾題

CHSH-nhspc112-PRI

CHSH X HARC

ysh 2023

A. Walk

給你一條線 y=ax+b

問你從 (0,0) 在剛好走 k 步的情況下有沒有辦法到達這條線

首先,可以發現如果前一次在線上,代表這次不可能在線上

所以,我們試圖讓點到達線上

也就是先求出點到線的（最短）計程車距離

因為斜率必為1或-1,於是直接比大小

最後看看k跟b的奇偶性是否相同即可

# Author : ysh
# 2023/07/27 Thu 17:03:44
import sys

input = sys.stdin.readline
print = sys.stdout.write

b = abs([int(i) for i in input().split()][1])
for i in range(int(input())):
    n = int(input())
    if n < b:
        print('NO\n')
        continue
    if n & 1 == b & 1:
        print('YES\n')
    else:
        print('NO\n')
quit()

B. Vendor

給你 n 個點

\displaystyle 請求出 \min \big[\sum_{k=1}^n \sqrt{(x - x_i)^2+(y - y_i)^2}\big]

問題

(x_i,y_i),\ 1 \leq i \leq n

爆搜

有一堆方法

O(4 \times 10^{12} \times n)\ O(2 \times 10^6 \times n)

Fun Fact

直接輸出第一個座標就可以獲得三分

但沒人要做

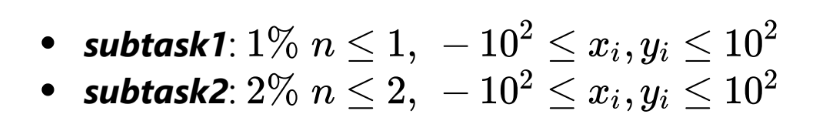
Fun Fact

爆搜就可以獲得 10 分

但同樣沒人要做

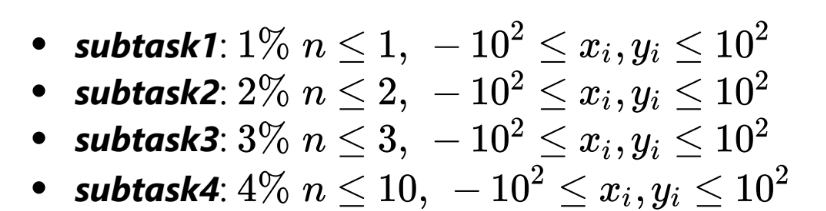
Fun Fact

有所有點都在同一條線上的測資

仍然沒人要做

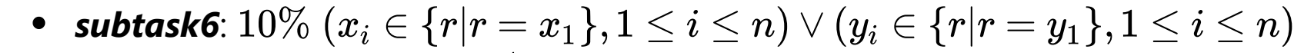
subtask 1,2

直接輸出第一個座標

subtask 3

算外心,找出附近四個點中總距離最小的

subtask 6

直接輸出最中間的那個座標

subtask 7

二分搜包二分搜

O(n (log_2^{2 \times 10^6})^2)

怎麼二分搜？

對 x 座標做二分搜

每次搜出

當 x 座標為 ?? 的時候

總距離最小值出現在哪裡

// Author : ysh
// 2023/08/03 Thu 14:22:59
#include<bits/stdc++.h>
using namespace std;
#define dt(i,j,k,l) ((i - k) * 1LL * (i - k) + (j - l) * 1LL * (j - l))
long double alldt(vector<pair<int,int>>&f,int x,int y) {
    long double ans = 0;
    for(auto &i : f) {
        ans = ans + sqrtl(abs(dt(i.first,i.second,x,y)));
    }
    return ans;
}
int check(vector<pair<int,int>>&f,int x,int l,int r) {
    if(l == r) return l;
    int mid = (l + r) >> 1;
    bool c = alldt(f,x,mid) > alldt(f,x,mid + 1);
    if(c) return check(f,x,mid + 1,r);
    else return check(f,x,l,mid);
}
int ck(vector<pair<int,int>>&f,int l,int r) {
    if(l == r) return l;
    int mid = (l + r) >> 1;
    int left = check(f,mid,-int(1e6),int(1e6));
    int right = check(f,mid + 1,-int(1e6),int(1e6));
    bool c = alldt(f,mid,left) > alldt(f,mid + 1,right);
    if(c) return ck(f,mid + 1,r);
    else return ck(f,l,mid);
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;cin>>n;
    vector<pair<int,int>>f(n);
    for(auto &i : f) {
        cin>>i.first>>i.second;
    }
    
    int x = ck(f,-int(1e6),int(1e6));
    int y = check(f,x,-int(1e6),int(1e6));

    cout<<x<<" "<<y<<"\n";
    return 0;
}

為什麼可以這麼做？

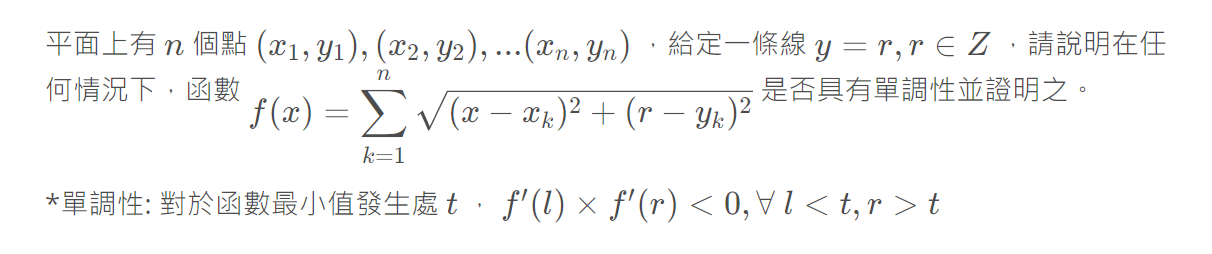
首先讓我們分開來看

\sqrt{(x - x_i)^2+(y - y_i)^2}

在 y 座標固定的情況下

是個凹函數

所以對 x 微分

[\sqrt{(x - x_i)^2+(y - y_i)^2}]'\\ = \frac{1}{2}[(x - x_i)^2+(y - y_i)^2] ^ {-\frac{1}{2}} \times 2(x - x_i)\\ = [(x - x_i)^2+(y - y_i)^2] ^ {-\frac{1}{2}}(x - x_i)\\ = \frac{(x - x_i)}{\sqrt{(x - x_i)^2+(y - y_i)^2}}

\displaystyle \text{let } \frac{(x - x_i)}{\sqrt{(x - x_i)^2+(y - y_i)^2}} = f'(x)\\ \frac{(x - x_i)}{\sqrt{(x - x_i)^2+(y - y_i)^2}} = 0\\ \lim_{x \rightarrow x_i-} f'(x) < 0 \text{ and } \lim_{x \rightarrow x_i+} f'(x) > 0\\ \text{When } x = x_i,\ f(x) \text{ has minimum value } f(x_i)

可得其為凹函數

由凹函數與凹函數相加為凹函數可知

\displaystyle\sum_{k = 1}^n \sqrt{(x - x_i)^2+(y - y_i)^2}

為凹函數

但是還是太慢了

嘿嘿我多卡了一個 log

有沒有發現

其實不用每次都對 y 座標做完整的二分搜

於是就誕生了另一套演算法

倍增

由二的次冪之和可以為任意正整數

可以推得

只需要不斷向上下左右移動二的次冪個單位

就可以不斷獲得最小值

從而達成整體最小值

// Author : ysh
// 2023/08/12 Sat 16:23:21
#include<bits/stdc++.h>
using namespace std;
const int xx[] = {-1,0,1,0};
const int yy[] = {0,1,0,-1};
vector<pair<int,int>>f;
#define dt(i,j) sqrtl((i.first * 1LL - j.first) * (i.first - j.first) + (i.second * 1LL - j.second) * (i.second - j.second))
long double alldt(pair<int,int>j) {
    long double ans = 0;
    for(auto &i : f) {
        ans = ans + dt(i,j);
    }
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;cin>>n;
    f = vector<pair<int,int>>(n);
    for(auto &i : f) {
        cin>>i.first>>i.second;
    }

    int mask = (1 << 20);
    pair<int,int>now = make_pair(0,0);
    long double ans = alldt({0,0});

    while(mask != 0) {
        for(int j = 1;j<=2;j++) {
            for(int i = 0;i<=3;i++) {
                auto pre = make_pair(now.first + (xx[i] * mask),now.second + (yy[i] * mask));
                auto t = alldt(pre);
                if(t < ans) {
                    ans = t;
                    now = pre;
                }
            }
        }
        mask = mask >> 1;
    }
    cout<<now.first<<" "<<now.second<<"\n";
    return 0;
}

結論

Mingyee 欠我一客冰炫風

F. Practice

首先

不唬爛這題來自AIME

DP
DPDP
Math

// Author : ysh
// 03/23/2023 Thu 14:00:18.03
#include<bits/stdc++.h>
using namespace std;
int check(int x,bool c = 0,bool d = 0) {
    if(x == 0) {
        return c;
    }
    int ans = 0;
    if(!c && d) ans += check(x - 1,1,1);
    if(!d) ans += check(x - 1,c,1);
    ans += check(x - 1,c,0);
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
 
    int n;cin>>n;
    cout<<check(n,0,0);
    return 0;
}

// Author : ysh
// 03/23/2023 Thu 14:00:18.03
#include<bits/stdc++.h>
using namespace std;
const int R = ((int) 1e9) + 7;
vector<int>mark;
#define int long long
int check(int x,bool c = 0,bool d = 0) {
    if(x == 0) {
        return c;
    }
    if(mark.at(((x - 1) << 2) + ((int) c << 1) + ((int) d)) != -1) return mark.at(((x - 1) << 2) + ((int) c << 1) + ((int) d));
    int ans = 0;
    if(!c && d) ans += check(x - 1,1,1);
    if(!d) ans += check(x - 1,c,1);
    ans += check(x - 1,c,0);
    return mark.at(((x - 1) << 2) + ((int) c << 1) + ((int) d)) = ans % R;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;cin>>n;
    mark.resize(n << 2,-1);
    cout<<check(n,0,0);
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
const int R = ((int) 1e9) + 7;
#define int long long
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;cin>>n;
    if(n == 2) {
        cout<<1;
        return 0;
    }
    vector<int>f(n);
    for(int i = 0;i<n;i++) {
        if(i == 0) f.at(0) = 1;
        else if(i == 1) f.at(1) = 2;
        else {
            f.at(i) = f.at(i - 1) + f.at(i - 2);
            f.at(i) = f.at(i) % R;
        }
    }
    long long ans = 0;
    for(int i = 1;i<=n - 3;i++) {
        ans = ans + (f.at(i - 1) * f.at(n - i - 3)) % R;
    }
    ans = ans + (f.at(n - 3) << 1);
    ans = ans % R;
    cout<<ans;
    return 0;
}

# Author : ysh
# 03/23/2023 Thu 13:56:24.23
import sys
R = int(1e9) + 7
a = [1,2]
n = int(sys.stdin.readline())
if n == 1:
    sys.stdout.write('0')
    quit()
if n == 2:
    sys.stdout.write('1')
    quit()
for i in range(2,n):
    a.append((a[len(a) - 2] + a[len(a) - 1]) % R)
ans = 0
for i in range(1,n - 2):
    ans = (ans + (a[i - 1] * a[n - i - 3]))
ans = ans + (a[n - 3] << 1)
ans = ans % R
sys.stdout.write(str(ans))

#include<bits/stdc++.h>
using namespace std;
const int R = (int) 1e9 + 7;
#define hck(i,j) check(i + j - 1,j)
#define int long long
int fp(int a,int b) {
    if(b == 0) return 1;
    int tmp = fp(a,b >> 1);
    if(b & 1) return (((tmp * tmp) % R) * a) % R;
    return (tmp * tmp) % R;
}
vector<int>mark({1});
int fl(int x) {
    if(mark.size() >= x + 1) return mark.at(x);
    mark.push_back((fl(x - 1) * x) % R);
    return mark.at(x);
}
int check(int a,int b) {
    return (((fl(a) * fp(fl(a - b),R - 1 - 1)) % R) * fp(fl(b),R - 1 - 1)) % R;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int n;cin>>n;
    n = n - 1;
    int ans = 0;
    for(int i = (n + 1) >> 1;i>=1;i--) {
        int left = n - (i - 1) - i;
        ans = ans + hck(i + 1,left) * i;
        ans = ans % R;
    }
    cout<<ans;
    return 0;
}

資訊學科能力競賽

A. Walk

B. Vendor

結論

F. Practice

DP DPDP Math

J. Balloon

DP
DPDP
Math