MUSIC and Improved MUSIC algorithm to Estimate Direction Arrival

Yung-Sheng Lu

MAR 01, 2018

@NCTU-CS

IEEE ICCSP 2015

Pooja Gupta, S. P. Kar

Outline

  • Abstract

  • Mathematical Model

  • The MUSIC Algorithm

  • Factors Influence

  • Improved MUSIC Algorithm

  • Conclusion

Abstract

Motivation

  • The effectiveness of the direction of arrival (DOA) estimation greatly determines the performance of smart antennas.
     

  • The accuracy in the estimation of DOA is very crucial in array signal processing.

Abstract

  • The MUSIC algorithm emphasized on a peak search method to estimate the arrival angle.

    • Array element spacing

    • Number of array elements

    • Number of snapshots

    • The signal incidence angle difference
       

  • The MUSIC algorithm has less efficiency for coherent signals.

DOA Estimation

  • The physical size of the operating antenna is inversely proportional to the antenna main lobe beam width.

    • Increasing the size of a single antenna is not practically feasible.

    • Antenna array provides better performances and signal reception.
       

  • Strengthen the useful signals by eliminating the noise signals and interference.

    • E.g., ESPRIT, MUSIC, WSF, MVDR, ML techniques and others.

DOA Estimation (cont.)

  • ESPRIT (Estimation of Signal Parameter via Rotational Invariance Techniques) and MUSIC (Multiple Signal Classification) are the two widely used spectral estimation techniques.

    • Decomposition of Eigen values

    • ESPRIT is applied to only array structures with some peculiar geometry.

    • MUSIC is used for both uniform and non-uniform linear arrays.

Mathematical Model

Assumptions

  •     narrowband source signals with same center frequency

  • Signals are impinging on an array of      sensor elements.

    • Consecutive linearly spaced with equal distances

    • The space matrix 

    •  

  • The number of sensor to be greater than the number of signals being incident, i.e.             .

  • The     signals are incident on the sensor with azimuth angles     .

    •  

F
FF
f_c
fcf_c
D
DD
d = \pi / 2
d=π/2d = \pi / 2
D > F
D>FD > F
1 \le k \le F
1≤k≤F1 \le k \le F
\theta_k
θk\theta_k
[d_1 \quad d_2 \quad ... \quad d_{D-1}]
[d1d2...dD−1][d_1 \quad d_2 \quad ... \quad d_{D-1}]
F
FF

Structure of an Antenna Array

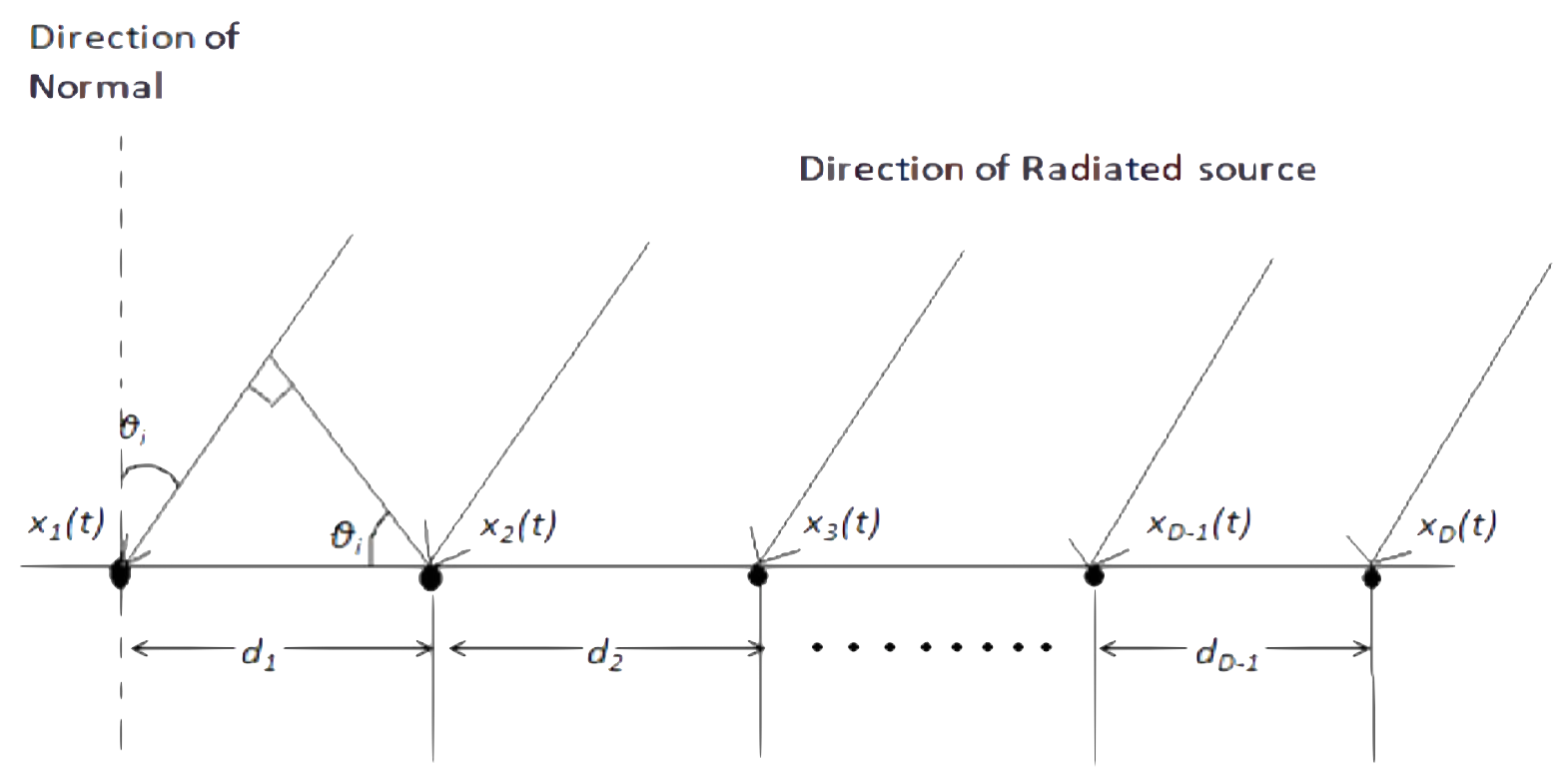
azimuth angles

source signals

sensor elements

D
DD
F
FF
\theta_k
θk\theta_k

Mathematical Model

  • The source signal in complex form

 

 

  • Consider the first element of the antenna array to be the reference

 

S_{\mathrm{source}}(t) = a_{\mathrm{amp}}(t)e^{j(f_c(t)+\phi(t))}
Ssource(t)=aamp(t)ej(fc(t)+ϕ(t))S_{\mathrm{source}}(t) = a_{\mathrm{amp}}(t)e^{j(f_c(t)+\phi(t))}
S_k(t)\mathrm{exp}\left({\frac{-j2 \pi d_p(p - 1) \sin \theta_k}{\pi}}\right)
Sk(t)exp(−j2πdp(p−1)sinθkπ)S_k(t)\mathrm{exp}\left({\frac{-j2 \pi d_p(p - 1) \sin \theta_k}{\pi}}\right)
1 \le k \le F
1≤k≤F1 \le k \le F

, where

Mathematical Model (cont.)

  • The total sensing at the       array due to all incoming signals is

     

     

p^{\mathrm{th}}
pthp^{\mathrm{th}}
J_p(t) = \displaystyle \sum_{k = 1}^{F} \mathrm{exp} \left( \frac{-j2 \pi d_p(p-1) \sin \theta_k}{\lambda} \right) S_k(t) + n_p(t)
Jp(t)=∑k=1Fexp(−j2πdp(p−1)sinθkλ)Sk(t)+np(t)J_p(t) = \displaystyle \sum_{k = 1}^{F} \mathrm{exp} \left( \frac{-j2 \pi d_p(p-1) \sin \theta_k}{\lambda} \right) S_k(t) + n_p(t)

, where

1 \le p \le D
1≤p≤D1 \le p \le D
d_{p-1}
dp−1d_{p-1}
x_{p-1}
xp−1x_{p-1}
x_{p}
xpx_{p}

The                and the      elements of the array are separated with a distance of      .

p^{\mathrm{th}}
pthp^{\mathrm{th}}
(p-1)^{\mathrm{th}}
(p−1)th(p-1)^{\mathrm{th}}
d_{p}
dpd_{p}

Mathematical Model (cont.)

  • The matrix representation of the received signal is


     

    •      is the steering vector matrix.



       

    •          is the noise received by all the elements.

    •                is the     signal source being incident on the elements.

       

A
AA
N(t)
N(t)N(t)
S_{\mathrm{source}}(t)
Ssource(t)S_{\mathrm{source}}(t)
F
FF
J(t) = A S_{\mathrm{source}}(t) + N(t)
J(t)=ASsource(t)+N(t)J(t) = A S_{\mathrm{source}}(t) + N(t)
J(t) = [J_1(t) \quad J_2(t) \quad ... \quad J_D(t)] ^ T
J(t)=[J1(t)J2(t)...JD(t)]TJ(t) = [J_1(t) \quad J_2(t) \quad ... \quad J_D(t)] ^ T
A = [\beta(\theta_1) \quad \beta(\theta_2) \quad ... \quad \beta(\theta_F)]
A=[β(θ1)β(θ2)...β(θF)]A = [\beta(\theta_1) \quad \beta(\theta_2) \quad ... \quad \beta(\theta_F)]
\beta(\theta_k) = [1 \quad \mathrm{exp} \left( \frac{-j2 \pi d_1 \sin \theta_k}{\lambda} \right) \quad ... \quad \mathrm{exp} \left( \frac{-j2 \pi d_{D-1}(D-1) \sin \theta_k}{\lambda} \right) ]
β(θk)=[1exp(−j2πd1sinθkλ)...exp(−j2πdD−1(D−1)sinθkλ)]\beta(\theta_k) = [1 \quad \mathrm{exp} \left( \frac{-j2 \pi d_1 \sin \theta_k}{\lambda} \right) \quad ... \quad \mathrm{exp} \left( \frac{-j2 \pi d_{D-1}(D-1) \sin \theta_k}{\lambda} \right) ]
S_{\mathrm{source}}(t) = [S_1(t) \quad S_2(t) \quad ... \quad S_F(t)] ^ T
Ssource(t)=[S1(t)S2(t)...SF(t)]TS_{\mathrm{source}}(t) = [S_1(t) \quad S_2(t) \quad ... \quad S_F(t)] ^ T

The MUSIC Algorithm

Schmidt with his colleagues proposed the Multiple Signal Classification (MUSIC) algorithm in 1979.

Introduction

  • The Eigen value decomposition of the received signal covariance matrix.
     

  • As this algorithm takes uncorrelated noise in to account, the generated covariance matrix is diagonal in nature.
     

  • The signal and the noise subspaces are orthogonal to each other.
     

  • This algorithm exploits the orthogonality to isolate the signal and noise subspaces.

The MUSIC Algorithm

  • The covariance matrix       for the received data J is the expectance of the matrix with its Hermitian equivalent.





     

    •       is the noise correlation matrix,                .
    •     is an unit matrix for the antenna array elements            .
R_J
RJR_J
R_J = \mathbb{E}[JJ^H]
RJ=E[JJH]R_J = \mathbb{E}[JJ^H]
= \mathbb{E} [(AS+N)[(AS+N)]^H ]
=E[(AS+N)[(AS+N)]H]= \mathbb{E} [(AS+N)[(AS+N)]^H ]
= A \mathbb{E} [SS^H] A^H + \mathbb{E} [NN^H]
=AE[SSH]AH+E[NNH]= A \mathbb{E} [SS^H] A^H + \mathbb{E} [NN^H]
= A R_S A^H + R_N
=ARSAH+RN= A R_S A^H + R_N
R_N
RNR_N
R_N = \sigma ^ 2 I
RN=σ2IR_N = \sigma ^ 2 I
I
II
D \times D
D×DD \times D

The MUSIC Algorithm (cont.)

  • In a practical scenario, the signals are associated with the noise, so now the computed correlation matrix along with noise is


     

    •       is the covariance matrix for the signal               .

    •      is the steering vector matrix.

R_S
RSR_S
A
AA
S_{\mathrm{source}}(t)
Ssource(t)S_{\mathrm{source}}(t)
R_J = A R_S A^H + R_N
RJ=ARSAH+RNR_J = A R_S A^H + R_N

The MUSIC Algorithm (cont.)

  • When this correlation matrix is decomposed it results in      number of Eigen values out of which the larger      Eigen values corresponds to the signal sources and the remaining smaller                     Eigen values are related to the noise subspace.


     

    •       is the basis for signal subspace.

    •        is the basis for noise subspace.

Q_S
QSQ_S
D
DD
F
FF
D - F
D−FD - F
Q_N
QNQ_N
R_J = Q_S \displaystyle \sum Q_S^H + Q_N \displaystyle \sum Q_N^H
RJ=QS∑QSH+QN∑QNHR_J = Q_S \displaystyle \sum Q_S^H + Q_N \displaystyle \sum Q_N^H

The MUSIC Algorithm (cont.)

  • As the MUSIC algorithm exploits the orthogonality between the signal and noise subspaces, the following holds true:


     

  • The DOA angle can be represented in terms of incident signal sources and the noise subspaces.

     

\beta^H(\theta)Q_N = 0
βH(θ)QN=0\beta^H(\theta)Q_N = 0
\theta_{\mathrm{MUSIC}} = \mathrm{min} \beta^H (\theta) Q_N Q_N^H \beta (\theta)
θMUSIC=minβH(θ)QNQNHβ(θ)\theta_{\mathrm{MUSIC}} = \mathrm{min} \beta^H (\theta) Q_N Q_N^H \beta (\theta)
P_{\mathrm{MUSIC}} = \displaystyle \frac{1}{\beta^H (\theta) Q_N Q_N^H \beta (\theta)}
PMUSIC=1βH(θ)QNQNHβ(θ)P_{\mathrm{MUSIC}} = \displaystyle \frac{1}{\beta^H (\theta) Q_N Q_N^H \beta (\theta)}

The MUSIC Algorithm (cont.)

Factors Influence

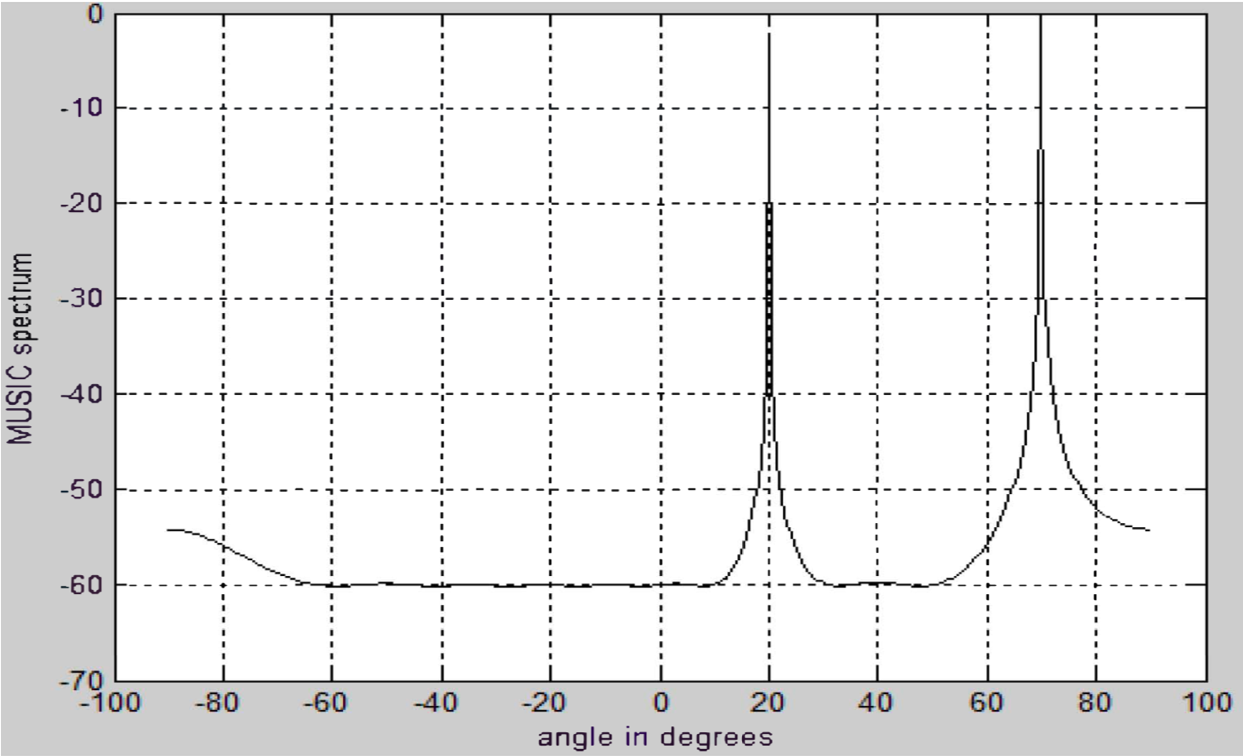
The Spacing between Array Elements

  • Consider an array with 10 elements and vary the spacing as
          ,        and     respectively

\lambda / 6
λ/6\lambda / 6
\lambda / 2
λ/2\lambda / 2
\lambda
λ\lambda

The spectrum losses efficiency when the element spacing is increased beyond       .

\lambda / 2
λ/2\lambda / 2

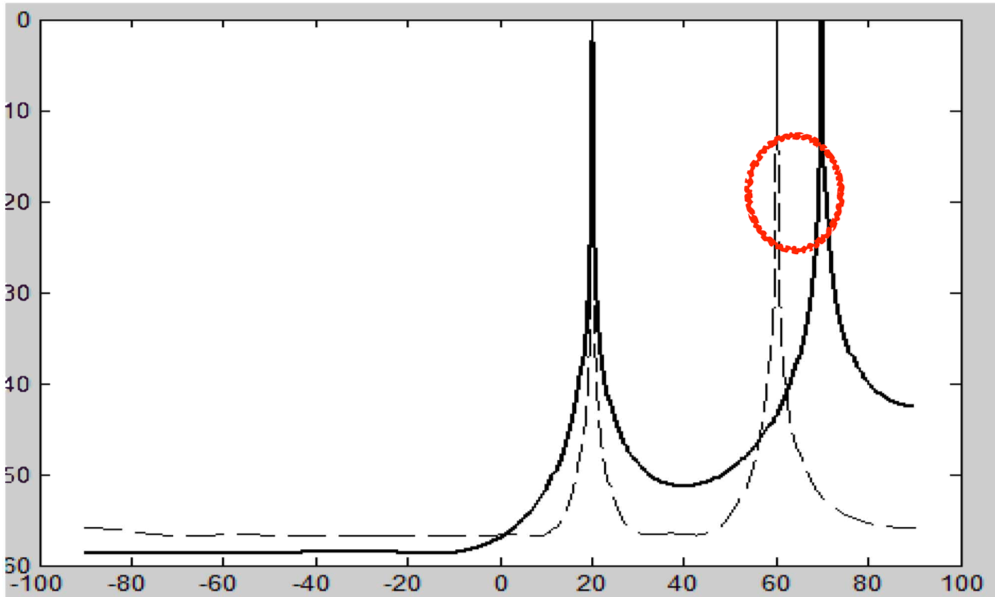
Number of Antenna Array

  • Consider the number of array elements is increased to 10, 20 and 30 respectively

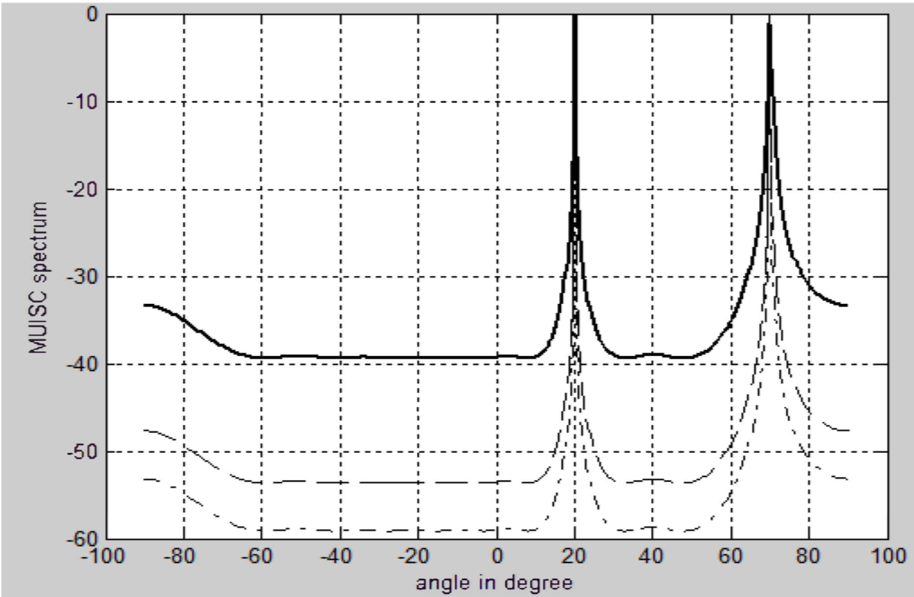
Number of Snapshots

  • Consider the number of snapshot is increased to 10, 20 and 30
    respectively

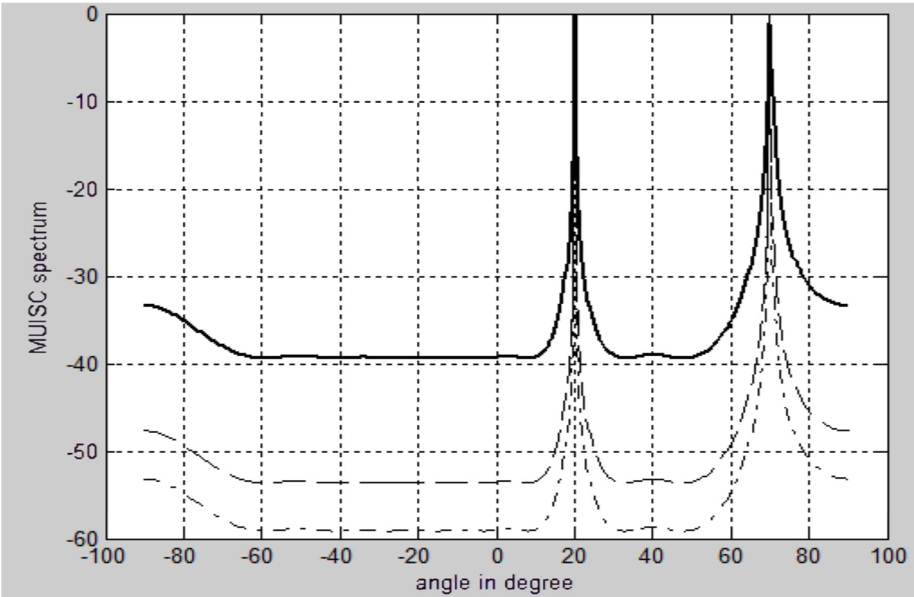
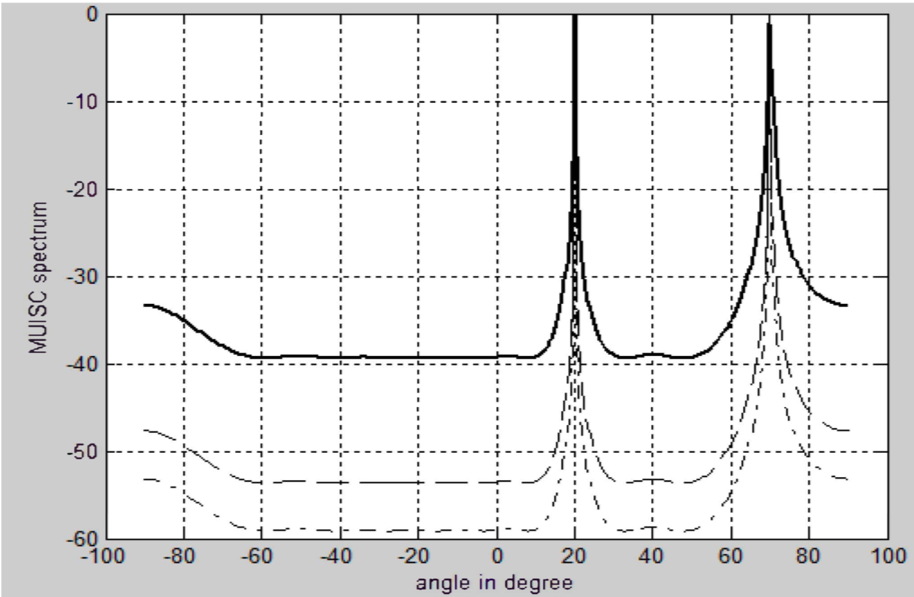
Signal Incidence Angle Difference

  • Consider the angle difference between the incoming signals is increased to       ,       and  

10 ^ \circ
10∘10 ^ \circ
15 ^ \circ
15∘15 ^ \circ
20 ^ \circ
20∘20 ^ \circ

Improved MUSIC Algorithm

Improved MUSIC Algorithm

  • MUSIC algorithm achieves high resolution in DOA estimation only when the signals are non-coherent.

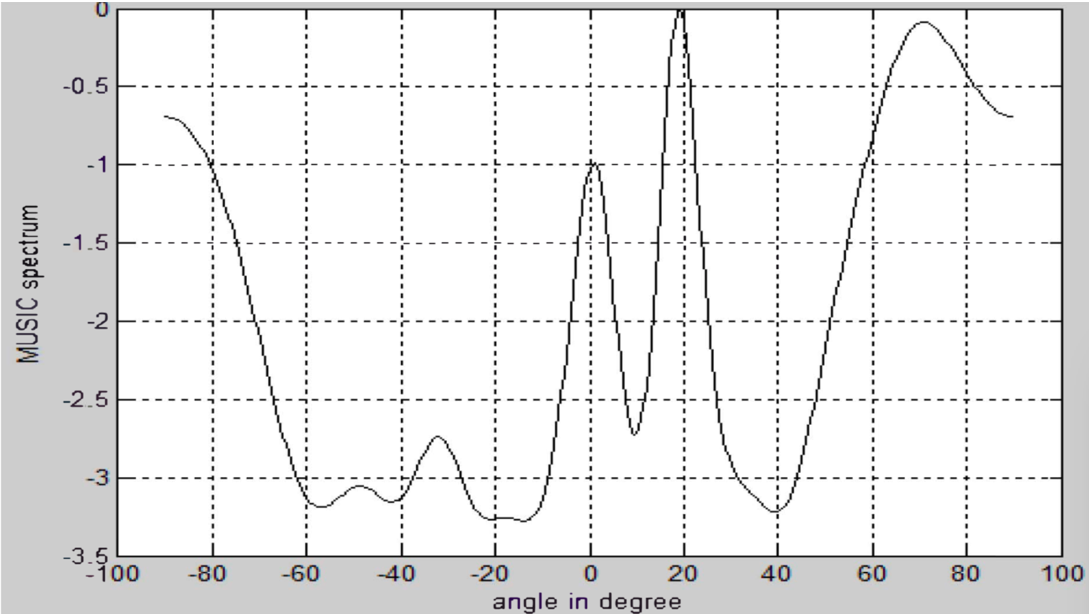
Improved MUSIC Algorithm (cont.)

  • Introduce an identity transition matrix     so that the new received signal matrix 

    •      is the complex conjugate of the original received signal matrix.

  • The matrix       and       can be summed up to obtain a reconstructed matrix     because they will have the same noise subspaces.

T
TT
X = TJ^*
X=TJ∗X = TJ^*
J^*
J∗J^*
R_X
RXR_X
R_J
RJR_J
R_X = \mathbb{E}[XX^H] = T R_J^*T
RX=E[XXH]=TRJ∗TR_X = \mathbb{E}[XX^H] = T R_J^*T
R
RR
R = R_X + R_J
R=RX+RJR = R_X + R_J
R = AR_SA^H + T[AR_SA^H]^*T + 2 \sigma ^ 2 I
R=ARSAH+T[ARSAH]∗T+2σ2IR = AR_SA^H + T[AR_SA^H]^*T + 2 \sigma ^ 2 I

Improved MUSIC Algorithm (cont.)

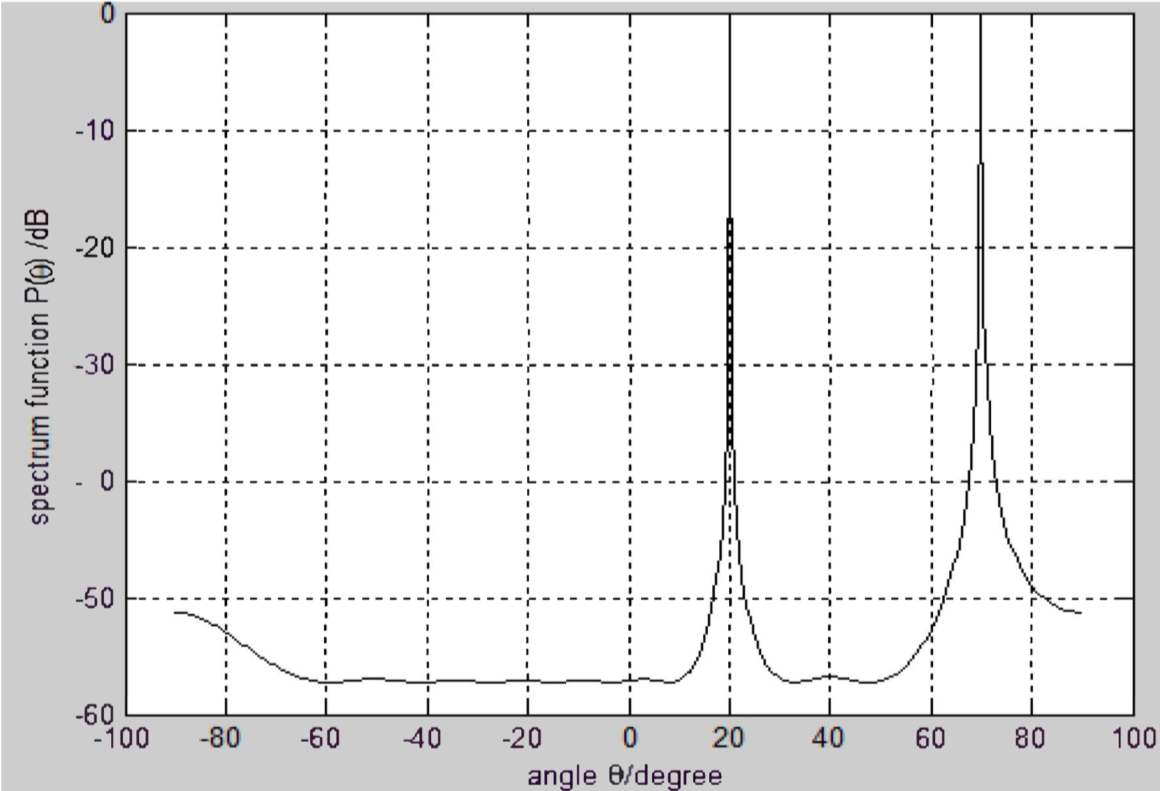
Conclusion

Conclusion

  • The MUSIC algorithm uses the Eigen values and Eigen vectors of the signal and noises to estimate the direction of arrival of the incoming signals.
     
  • Efficiency of this estimation algorithm can be improved by modifying some parameters.
     
  • An improved MUSIC algorithm can be implemented for coherent signals as well.
Made with Slides.com