Anomaly Detection for

Time Series

Yung-Sheng Lu

Apr 11, 2017

@NCKU-CSIE

Outline

Problem Setting
Challenges
Types of Time Series
Existing Techniques
Transformation of Data
Detection Techniques
Discord Detection

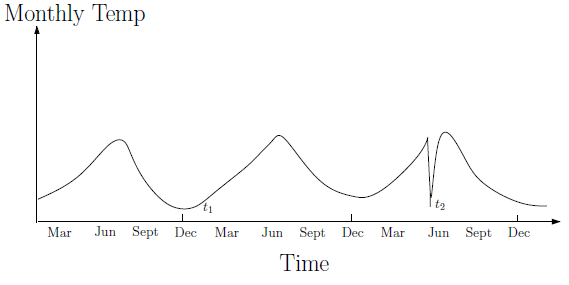
Problem Setting

Detecting contextual anomalies in the time series
The anomalies are the individual instances of the time series which are anomalous in a specific context, but not otherwise.

Problem Setting (cont.)

Detecting anomalous subsequence within a given series
Find an anomalous subsequence with respect to a given long sequence (time series).

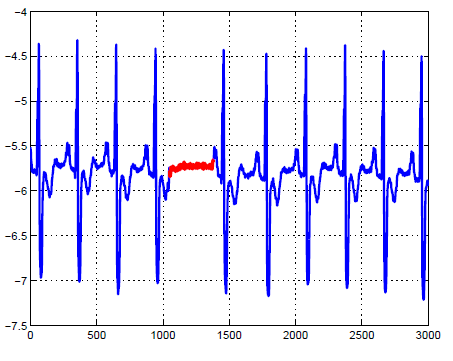
discords

Problem Setting (cont.)

Detecting anomalous time series base on a time series data base
- Determine if a test time series is anomalous with respect to a database of training time series.
- This database can be of two types.
  - Only normal time series
    - semi-supervised setting
  - Both normal and anomalous data
    - unsupervised anomaly detection

Challenges

Many ways in which an anomaly occurring in a time series may be defined.
For detecting anomalous subsequences, the exact length of the subsequence is often unknown.
The training and test time series can be of different lengths.
Best similarity/distance measures which can be used for different types of time series is not easy to determine.

Challenges (cont.)

Performances of many anomaly detection algorithms are highly susceptible to noise in the time series data, since it is hard to differentiating anomalies from noise.
Time series in real applications are usually long and as the length increases the computational complexity also increases.
Many anomaly detection algorithms expect multiple time series to be at a comparable scale in magnitude while for most of the data it is not true.

Types of Time Series

In most of the techniques in this survey
- Training data to learn a model for normal behavior
- Test data is assigned an anomaly score based on the model.
Two key characteristics of time series
- periodicity
- synchronous

Types of Time Series (cont.)

Periodic and Synchronous

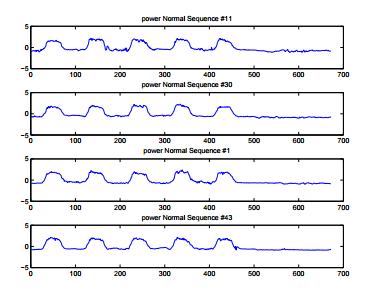
Types of Time Series (cont.)

Aperiodic and Synchronous

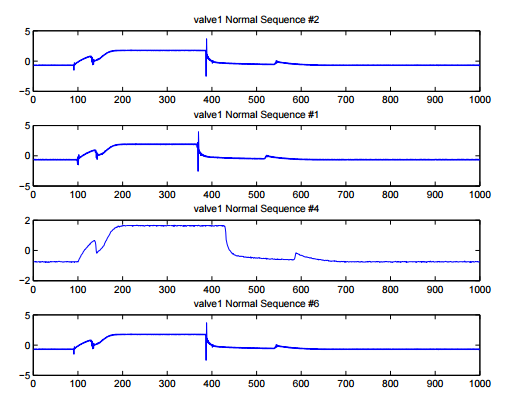
Types of Time Series (cont.)

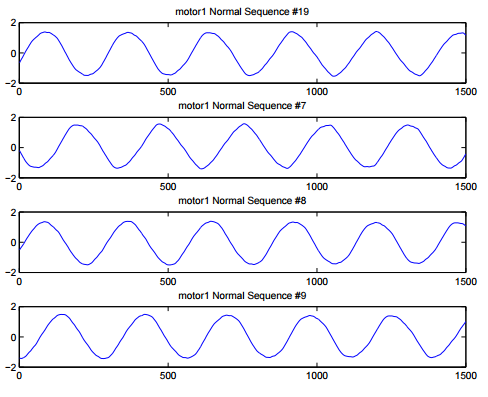
Periodic and Asynchronous

Types of Time Series (cont.)

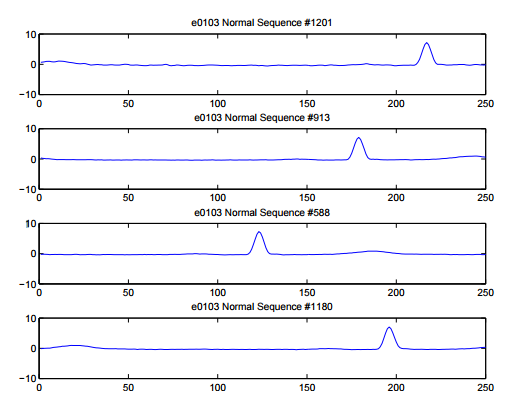
Aperiodic and Asynchronous

Existing Techniques

Overview

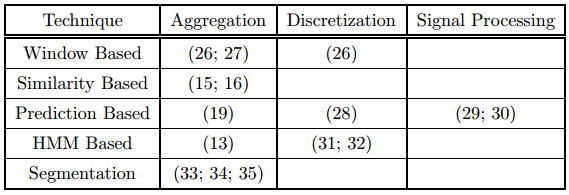
Anomaly detection techniques can be classified
- Procedural dimension
  the process of finding anomalies
- Transformation dimension
  the data is transformed prior to anomaly detection.
Both these dimensions are orthogonal.

Overview (cont.)

Window-based and similarity-based methods
Build a lazy learning model which compares the test time series with the given training time series for assigning anomaly scores.
HMM-based and Regression-based methods
Build parametric models on the training data which probabilistically assign anomaly scores to a test time series.
Segmentation-based methods
Build a finite state automaton on the given training data and predict the state of the test time series.

Overview (cont.)

Aggregation-based transformation
Focus on dimensionality reduction by aggregating consecutive values.
Discretization-based and Signal-processing-based transformations
Reduce the dimensionality of the data in different ways and transform the input data into a different domain which can be used to obtain computational efficiency.

Transformation of Data

Motivation

Exist many challenges associated with handling time series.
- high-dimensionality, noise, scaling etc.
To achieve computational efficiency.

Before Start

Many anomaly detection algorithms expect multiple time series to be at a comparable scale.
- Normalize the data
  Each attribute contributes uniformly for the similarity.

Aggregation

Compress a time series by replacing a set of consecutive values by a representative value of them.
- usually use the average
- deals with the time domain of the time series
Benefits
- reduces dimensionality of the data
- the resulting time series is smoother
  - masks noise and missing values

Discretization

Convert the given time series into a discrete sequence of finite alphabets.
- deals with the amplitude domain of the time series
- cause loss of information
Steps
- Divide the amplitude range into different bins
- Assign a symbol to each of the bin
- Transform the time series by replacing every data point

Discretization (cont.)

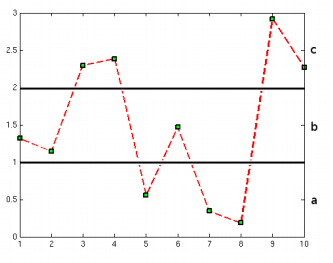
Example
- The time series amplitude (0-3) is divided into 3 equal sized bins and assigned a, b, c.
- The symbolic representation would be bbccabaacc

Signal Processing

Like Fourier transforms, wavelet transforms help to obtain this entirely different space of coefficients where the data can be analyzed
- used to get a lower dimensional representation of time series
Haar Transform
- A sequence of averaging and differencing operations on the consecutive values of a discrete time function.
- Preserves the Euclidean distance between two time series.

Detection Techniques

Overview

The process of anomaly detection
- Compute the anomaly scores of individual observations or subsequences of a given test time series using a detection technique.
- Aggregate these anomaly scores to calculate the anomaly score of the given test time series.
  - mean of all the anomaly scores
  - mean of top k anomaly scores
  - mean of log of anomaly scores
  - number of times the running average of the anomaly scores exceeds a threshold

Window-based

Divide the given time series into fixed size windows (subsequences) to localize the cause of anomaly within one or more windows.
An anomaly can be caused due to the presence of one or more anomalous subsequences.

Proximity-based

The pairwise proximity between the test and training time series using an appropriate distance or similarity kernel to compute the anomaly score of the test time series.
The anomalous time series are different from the normal ones.
- can be captured using a proximity measure.