Scilab
Alunos: Lucas Roth, Vinicius Brignoli de Souza e Yuri Possamai

Scilab
Scilab é um ambiente voltado para o desenvolvimento de software para resolução de problemas numéricos. O Scilab foi criado em 1990 por um grupo de pesquisadores do INRIA.


Sobre
É uma plataforma computacional científica, voltada para a computação numérica, muito semelhante ao seu "primo" Matlab

Principais características desse ambiente de programação :
-Aplicação de programação em linguagem matemática de simples usabilidade, com poucas linhas de código, para geração de gráficos bi e tridimensionais, inclusive com animações;
-Manipulações com matrizes são facilitadas por diversas funções implementadas nas caixas de ferramentas;
-Permite trabalhar com polinômios, funções de transferência, sistemas lineares e gráficos;
-Define funções facilmente;
-É um software livre, de código aberto, multi-plataforma (Linux, WIndows e Mac OS)

Operações Primárias
Existem duas formas de interação com o software:
- Digitação diretamente no prompt;
- Programação numérica propriamente dita;
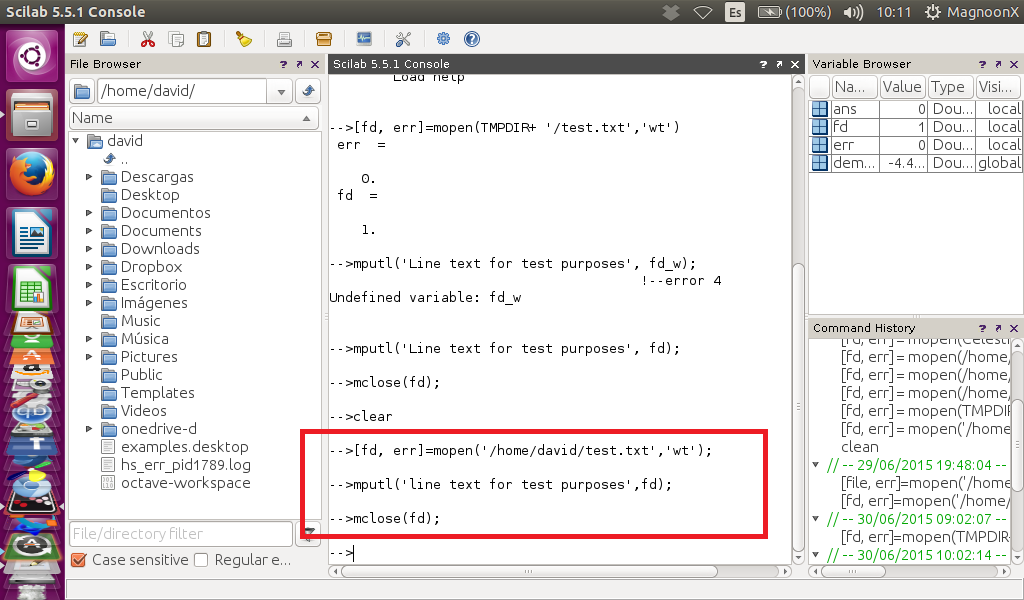

Operações Primárias
A primeira instrução a respeito do prompt é quanto ao uso do ponto e vírgula:
- Interpreta o fim da execução da linha de comando;
- O resultado da operação fica mascarado para o usuário;

Operações Primárias
Se não for escrito o ponto e vírgula.
- A quebra de linha vai denotar fim da execução;
- O resultado será exibido para o usuário;
Ambas as formas têm sua aplicação.
Outra observação importante é que o Scilab é case sensitive.

Operações Matemáticas.
As variáveis matemáticas usadas no Scilab são vetores complexos.
O número imaginário é denotado por %i e, seguindo a notação padrão de um número complexo z = a+bi, temos as seguintes operações possíveis:
- Soma - "+"
- Subtração - "-"
- Multiplicação - "*"
- Divisão à direita - "/"
- Divisão à esquerda - "\"
- Potenciação - "^"

Comandos de Fluxos
Os laços são, de longe, a parte mais importante para se programar com o Scilab, e os reconhecidos pelo ambiente são if, for e while. E seguem as seguintes lógicas.
- For: para um determinado índice variando de um valor inicial até um valor final com um determinado incremento, execute os comandos definidos.

Comandos de Fluxos
- If: caso a condição seja verdadeira executa os comandos, pode
ser agregados dois outros comandos: elseif e if ;
- While : funciona como um misto dos outros dois, na medida
em que são executados comandos até que uma condição não seja mais satisfeita.

Polinômios
Esta é uma classe de variáveis, tal como real ou lógica. um polinômio é gerado através da função poly.
Existem duas formas de se criar um polinômio: para a primeira forma, são permitidas três sintaxes:
P=poly([a b],'s');
P=poly([a b], 's', 'r');
P=poly([a b], 's', 'roots');
Polinômios
Quando se deseja a segunda alternativa, as opções são apenas duas:
P=poly([c d], 's', 'c');
P=poly([c d], 's', 'coeff'); 
Funções
São procedimentos sintetizados em uma só operação de comando. Considerando a operação de obter os números pares até um número N. Podemos sintetizá-la em uma função, por exemplo pares. Os comandos obrigatórios para a definição de uma função são function outputs=nome_da_função (inputs) e endfunction.

Funções
function n=pares(N)
n=0;
for i=1:N
if modulo(i,2)==0
n=n+1;
end
end
endfunction 
Gráficos
Gráficos bidimensionais – São constituídos de dois eixos, sendo necessário, portanto, dois argumentos de entrada para a execução, que, na verdade, são vetores com a mesma dimensão.

Gráficos
As funções responsáveis pela plotagem 2D são plot, plot2d, fplot2d e contour2d.
O comando plot2d plota uma curva bidimensional. Aceita quatro especificações (considere um eixo –x definido de 0 a 5):

Gráficos
plot2d1: plotagem padrão (linear):
clc
clear
close
x=0:.01:5;
y=sin(x.^2);
plot2d1(x,y)plot2d1: plotagem padrão (linear):
clc
clear
close
x=0:.01:5;
y=sin(x.^2);
plot2d1(x,y)
Gráficos
plot2d3: plotagem em barras verticais:
clc
clear
close
x=0:.05:5;
y=sin(x.^2);
plot2d3(x,y)plot2d4: plotagem em setas:
clc
clear
close
x=0:.05:5;
y=sin(x.^2);
plot2d4(x,y)

Gráficos
clc
clear
close
t= 0:.01:2*%pi;
polarplot(sin(2*t),cos(5*t));O comando polarplot plota o gráfico em coordenadas polares

Gráficos
clc
clear
close
t=[0:0.1:2*%pi]';
z=(sin(t).*exp(t))*cos(t');
plot3d(t,t,z)Gráficos tridemensionais: O comando mais utilizado é o plot3d.
O seu uso pode ser observado na rotina a seguir:
