Safety and Efficiency in Autonomous Vehicles through Planning with Uncertainty

Zachary Sunberg

May 25, 2018

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Controlling an Autonomous Vehicle is inherently a multi-objective problem

EFFICIENCY

SAFETY

Minimize resource use

(especially time)

Minimize the risk of harm to oneself and others

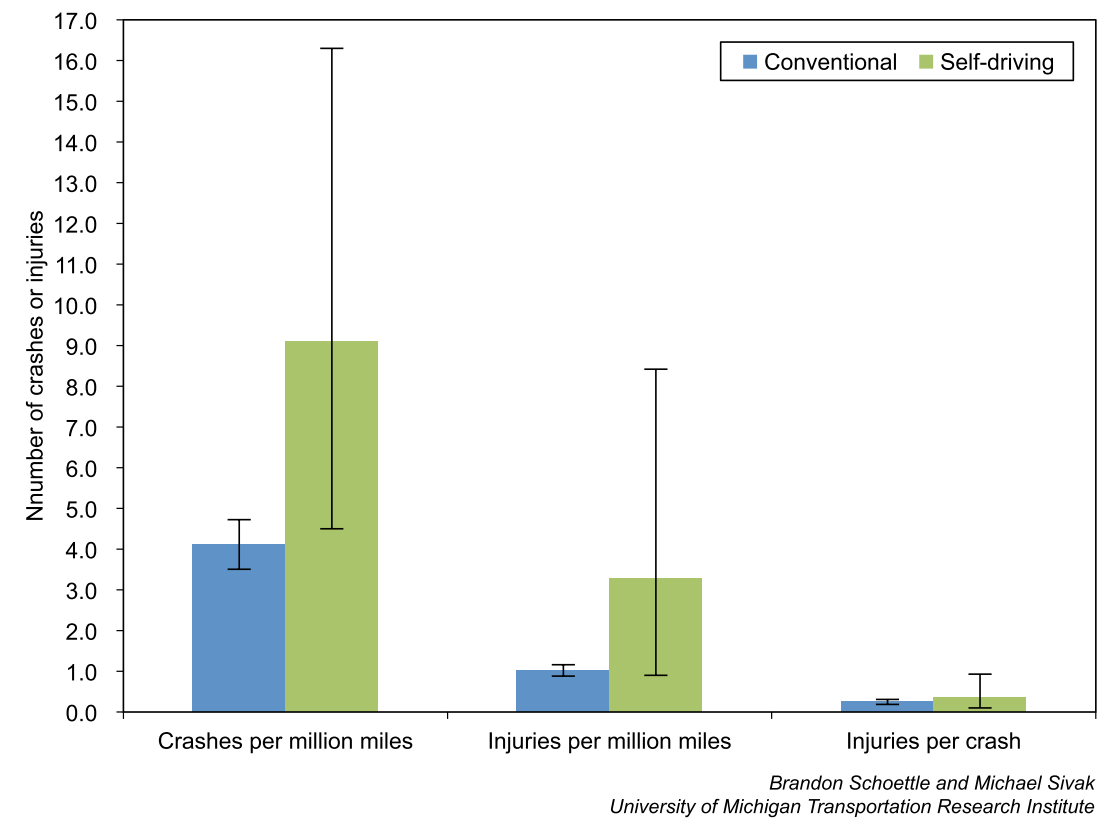
Shoettle and Sivak, "A Preliminary Analysis of Real-World Crashes Involving Self-Driving Vehicles" UMTRI-2015-34

Two extremes:

Objective Function

$$R(s_t, a_t) = R_\text{E}(s_t, a_t) + \lambda R_\text{S}(s_t, a_t)$$

Safety

Weight

Efficiency

\[\text{maximize} \quad E \left[ \sum_{t=0}^\infty \gamma^t R(s_t, a_t) \right]\]

Objective Function

Safety

Better Performance

Model $M_2$, Algorithm $A_2$

Model $M_1$, Algorithm $A_1$

Efficiency

$$R(s_t, a_t) = R_\text{E}(s_t, a_t) + \lambda R_\text{S}(s_t, a_t)$$

Safety

Weight

Efficiency

Dynamic Model: Types of Uncertainty

OUTCOME

MODEL

STATE

Markov Model

$\mathcal{S}$ - State space
$T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}$ - Transition probability distributions

Markov Decision Process (MDP)

$\mathcal{S}$ - State space
$T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Transition probability distribution
$\mathcal{A}$ - Action space
$R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Reward

Partially Observable Markov Decision Process (POMDP)

$\mathcal{S}$ - State space
$T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Transition probability distribution
$\mathcal{A}$ - Action space
$R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Reward
$\mathcal{O}$ - Observation space
$Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}$ - Observation probability distribution

Contributions

Quantified the performance price of certifiability for a UAV collision avoidance system and showed how to reduce it.

Quantified the safety and efficiency advantage of planning with internal states.

Developed online algorithms for continuous POMDPs.
1. Showed that current solvers and naive double progressive widening are suboptimal.
2. Used weighted particle filtering to achieve first performance better than QMDP with POMCPOW.

Led development of POMDPs.jl

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Trusted and Optimized UAV Collision Avoidance

Challenge: Certification

Government agencies and vehicle operators often seek certification that a control system will never command a near mid-air collision (NMAC).
Simple, deterministic algorithms are much easier to certify.

Trusted Resolution Logic

Additional buffer compensates for uncertainty

1.0

1.5

2.0

3.0

4.0

MDP Formulation

Transition: $\quad \dot{\psi}^{(o)}_t = \frac{g \, \tan \phi^{(o)}_t}{v^{(o)}}$, $\quad \dot{\psi}^{(i)}_t \sim \mathcal{N}(0, 10^\circ/s)$

Ownship State

Intruder State

Bank Angle

$s=\left(x^{(o)}, y^{(o)}, \psi^{(o)}, x^{(i)}, y^{(i)}, \psi^{(i)}, \text{dev}\right)$

$a = \phi^{(o)}$, $\mathcal{A} = \{-45^\circ, -22.5^\circ, 0^\circ, 22.5^\circ, 45^\circ\}$

$R(s, a) = -c_\text{step} + r_\text{goal} \, \text{in\_goal}(s) - c_\text{dev} \, \text{dev}(s,a) - \lambda \,\text{nmac}(s) $

Efficiency

Safety

Solving MDPs and POMDPs - The Value Function

$$\mathop{\text{maximize}} V_\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \bigm| s_0 = s, a_t = \pi(s_t) \right]$$

$$V^*(s) = \max \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$

\pi: \mathcal{S} \to \mathcal{A}

Involves all future time

Involves only $t$ and $t+1$

$a \in \mathcal{A}$

Features

\[\tilde{V}(s) = \beta(s)^\top \theta\]

\[\tilde{V}_{k+1}(s) = \Pi \mathcal{B}[\tilde{V}_k](s)\]

$45^\circ$

$-45^\circ$

$\phi=0^\circ$

Sunberg, Zachary N., Mykel J. Kochenderfer, and Marco Pavone. "Optimized and trusted collision avoidance for unmanned aerial vehicles using approximate dynamic programming." Robotics and Automation (ICRA), 2016 IEEE International Conference on. IEEE, 2016.

Value Function

Policy

Price of certifiability

Trusted Resolution Logic

Directly Optimized Turn Rate

Maintaining certifiability

\[\tilde{\mathcal{A}}(s) = \left\{a \in \mathcal{A} \mid \text{mindist}(s, a) \geq D_\text{NMAC} \right\}\]

Price of certifiability

Trusted Resolution Logic

Directly Optimized Turn Rate

Trusted Optimized Turn Rate

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Sadigh, Dorsa, et al. "Information gathering actions over human internal state." Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference on. IEEE, 2016.

Schmerling, Edward, et al. "Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction." arXiv preprint arXiv:1710.09483 (2017).

Sadigh, Dorsa, et al. "Planning for Autonomous Cars that Leverage Effects on Human Actions." Robotics: Science and Systems. 2016.

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

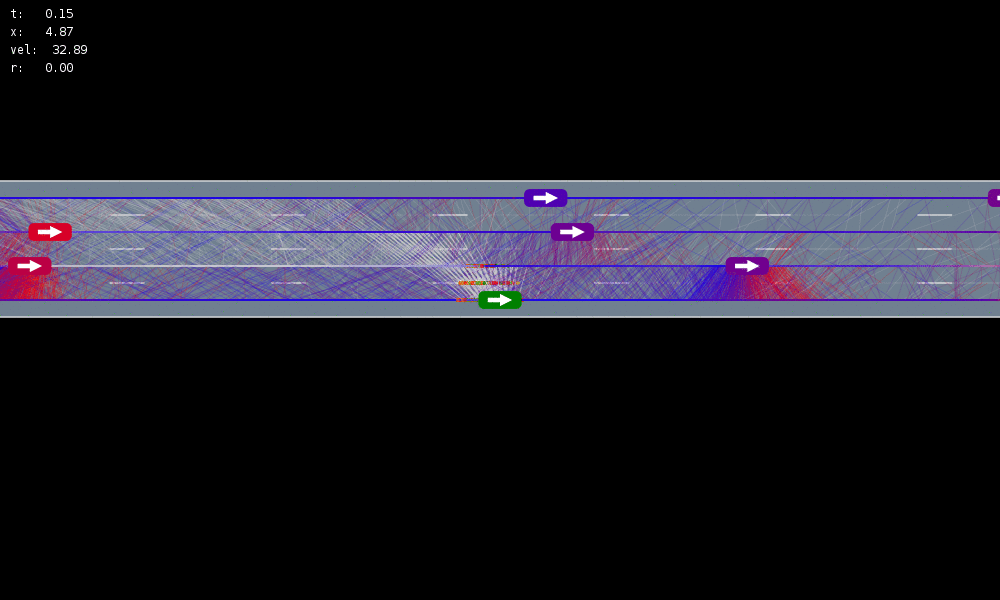
Human Behavior Model: IDM and MOBIL

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]

g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).

A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).

A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).

POMDP Formulation

$s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)$

$o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}$

$a = (\ddot{x}, \dot{y})$, $\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}$, $\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}$

R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states of other cars

Actions filtered so they can never cause crashes
Braking action always available

Efficiency

Safety

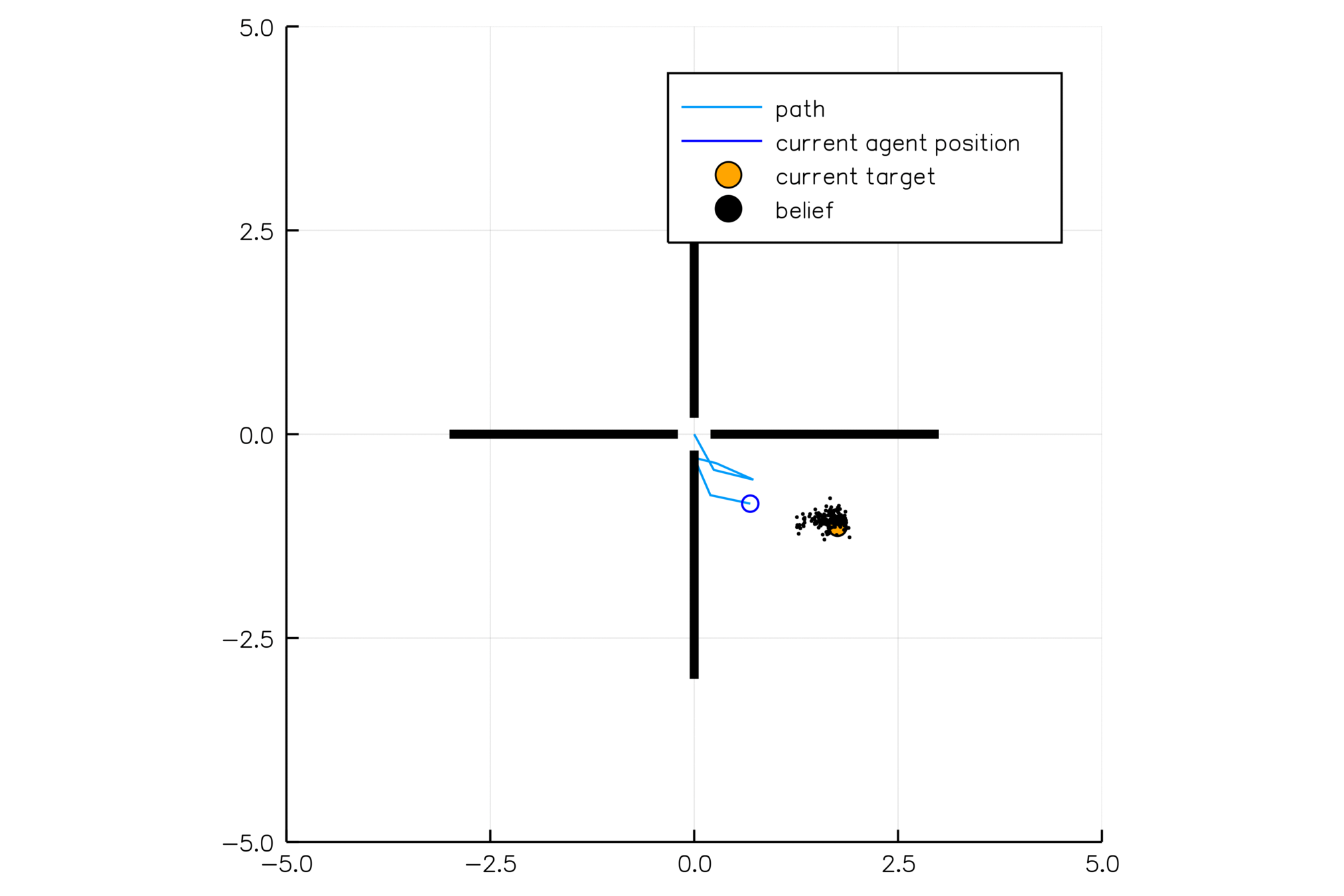
Belief

History: all previous actions and observations

\[h_t = (b_0, a_0, o_1, a_1, o_2, ..., a_{t-1}, o_t)\]

Belief: probability distribution over $\mathcal{S}$ encoding everything learned about the state from the history

\[b_t(s) = P(s_t=s \mid h_t)\]

A POMDP is an MDP on the belief space

Solving MDPs and POMDPs - Offline vs Online

ONLINE

OFFLINE

Value Iteration

Sequential Decision Trees

QMDP

\[Q_{MDP}(b, a) = \sum_{s \in \mathcal{S}} Q_{MDP}(s,a) b(s) \geq Q^*(b,a)\]

Equivalent to assuming full observability on the next step

Will not take costly exploratory actions

$$Q_\pi(b,a) = E \left[ \sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \bigm| s_0 = s, a_0 = a\right]$$

All drivers normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Simulation results

All drivers normal

Omniscient

Mean MPC

QMDP

POMCPOW

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Monte Carlo Tree Search

Image by Dicksonlaw583 (CC 4.0)

POMCP

Uses simulations of histories instead of full belief updates

Each belief is implicitly represented by a collection of unweighted particles

Silver, David, and Joel Veness. "Monte-Carlo planning in large POMDPs." Advances in neural information processing systems. 2010.

Ross, Stéphane, et al. "Online planning algorithms for POMDPs." Journal of Artificial Intelligence Research 32 (2008): 663-704.

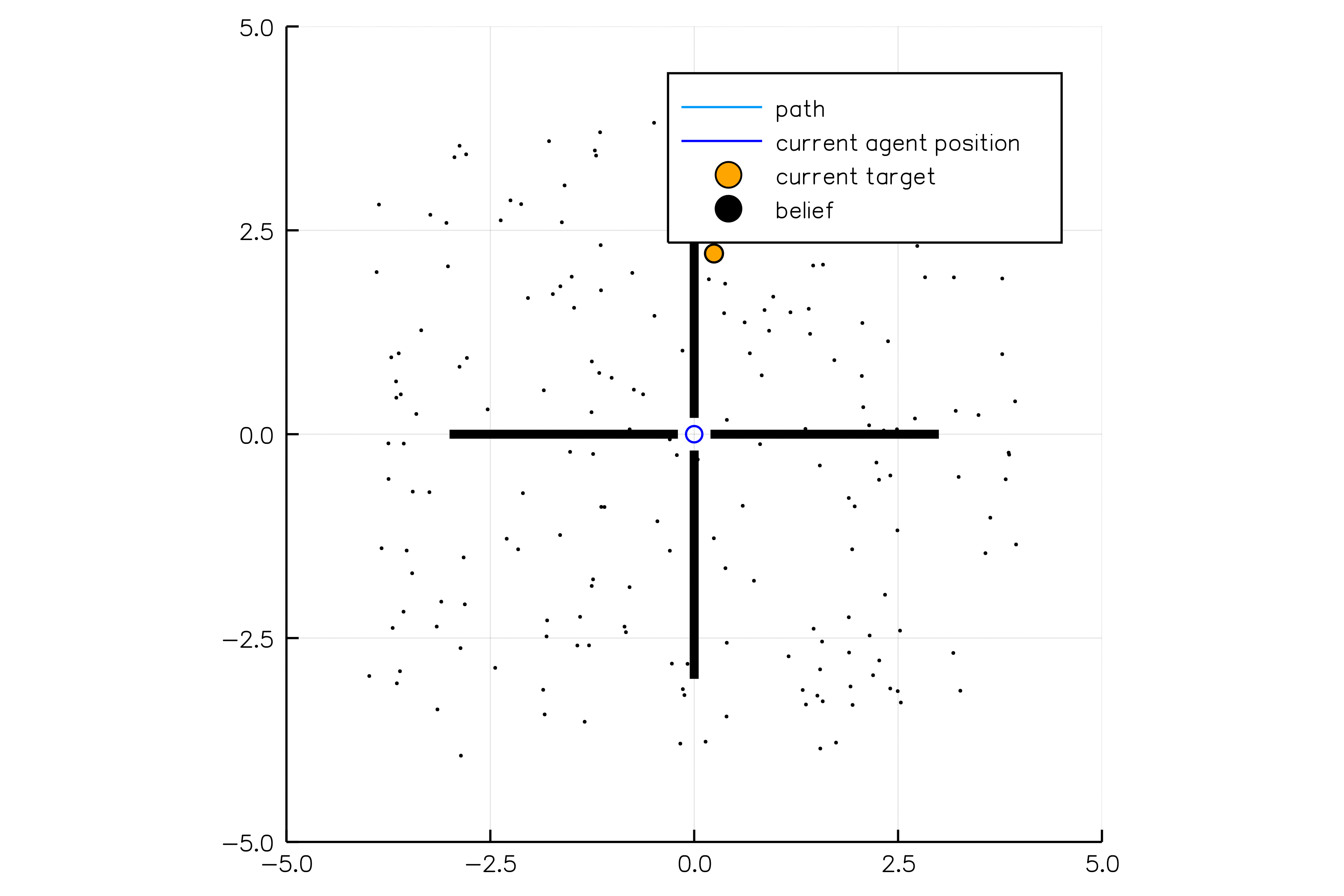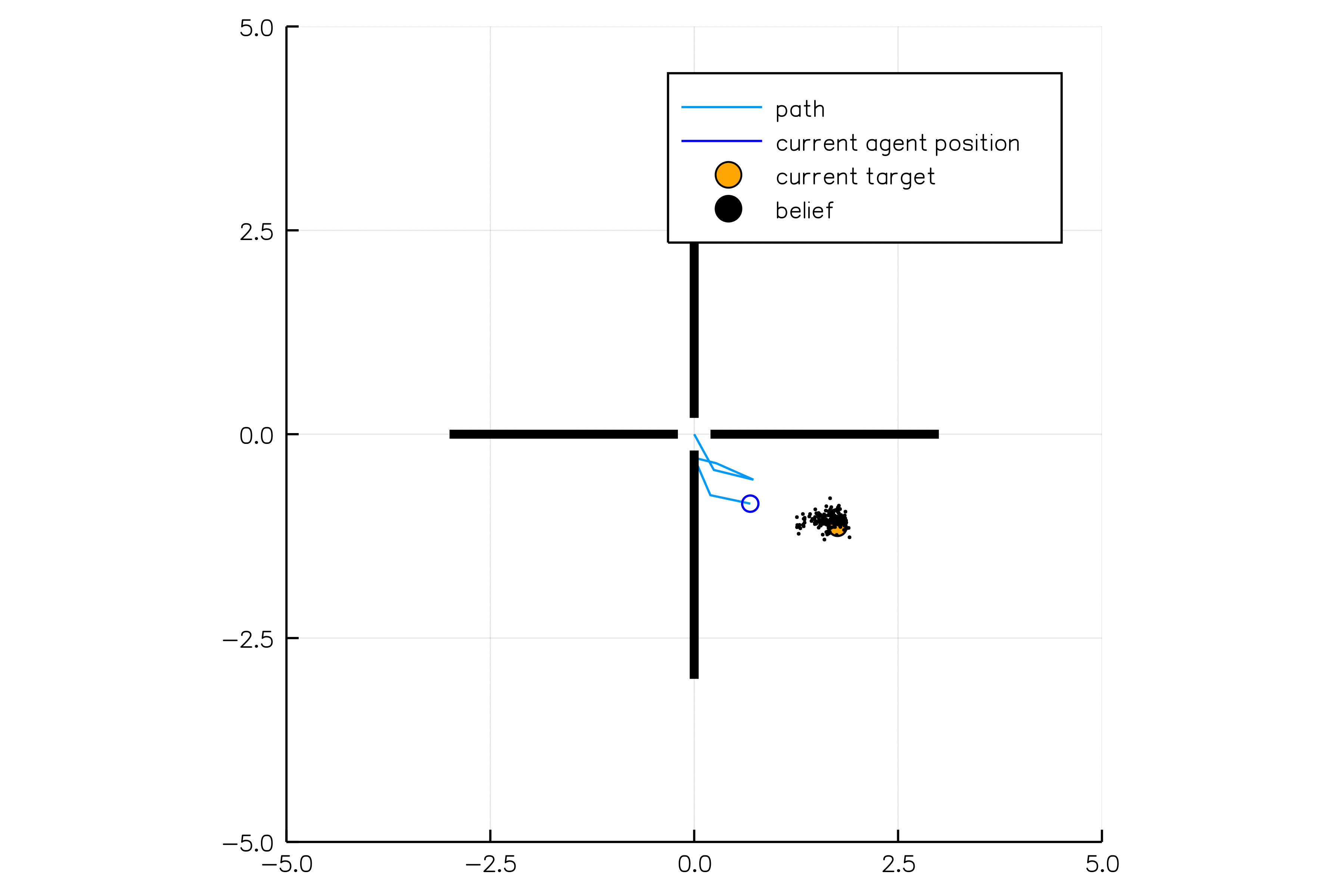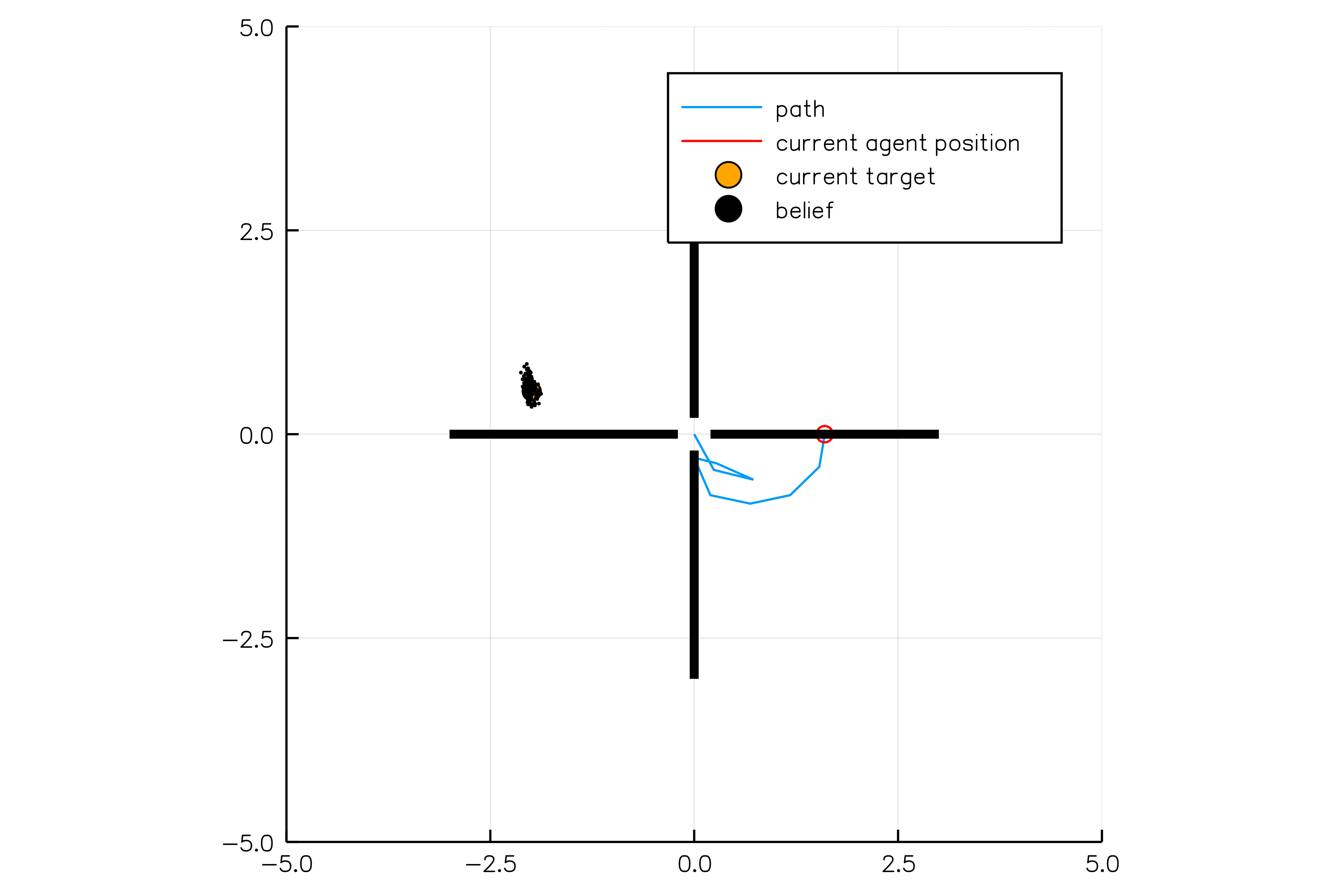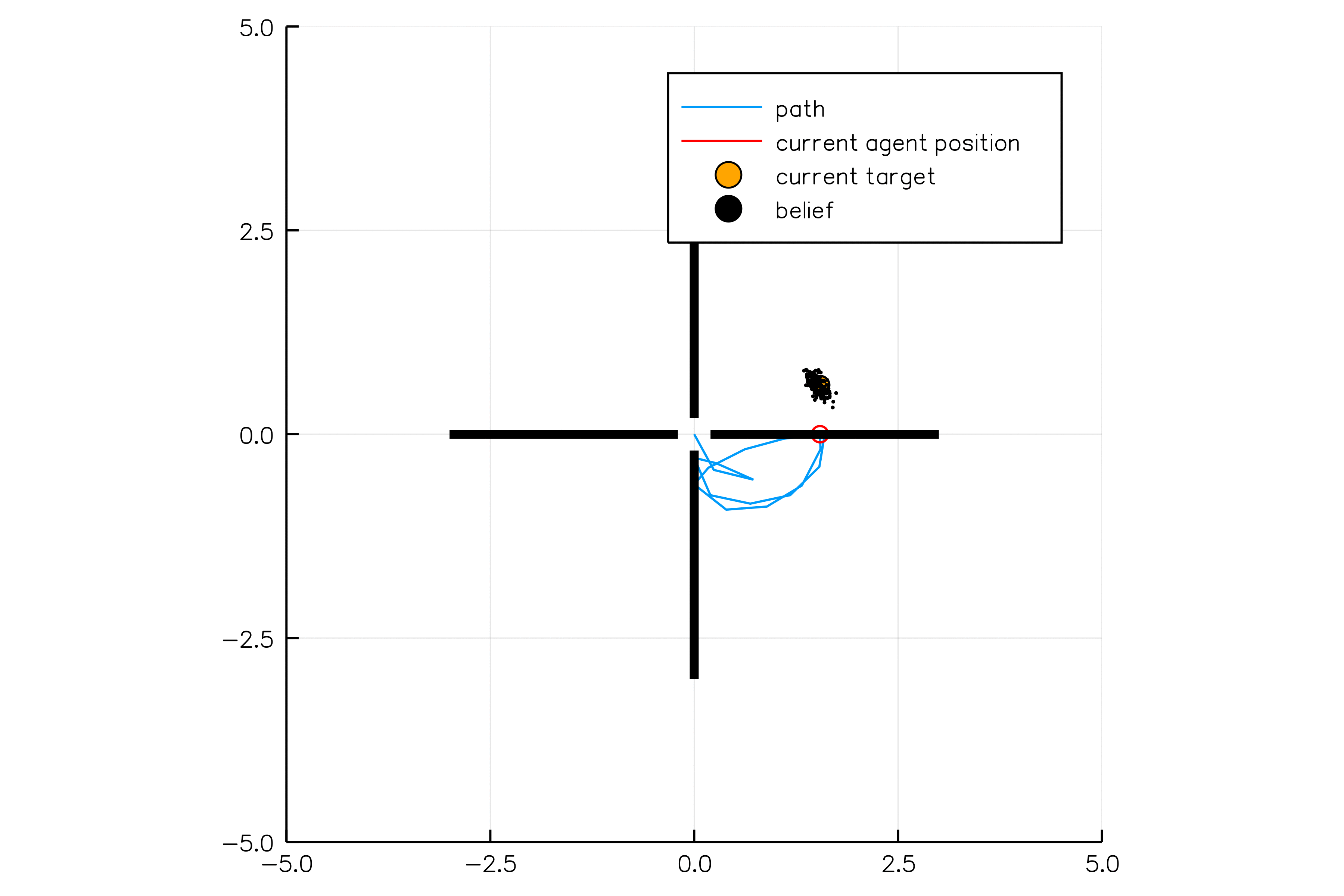
Light-Dark Problem

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

Goal: $a=0$ at $s=0$

Optimal Policy

Localize

$a=0$

[ ] An infinite number of child nodes must be visited

[ ] Each node must be visited an infinite number of times

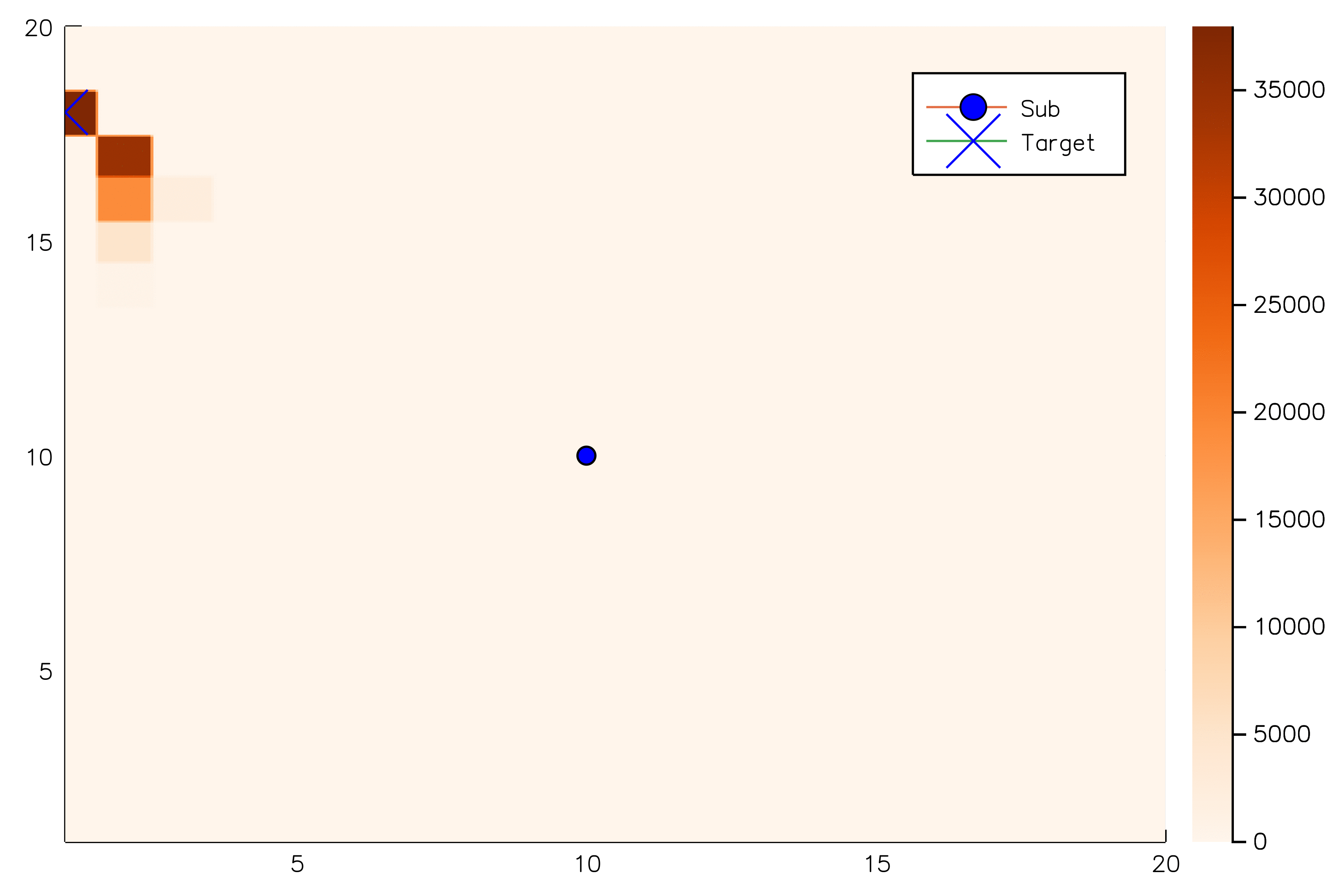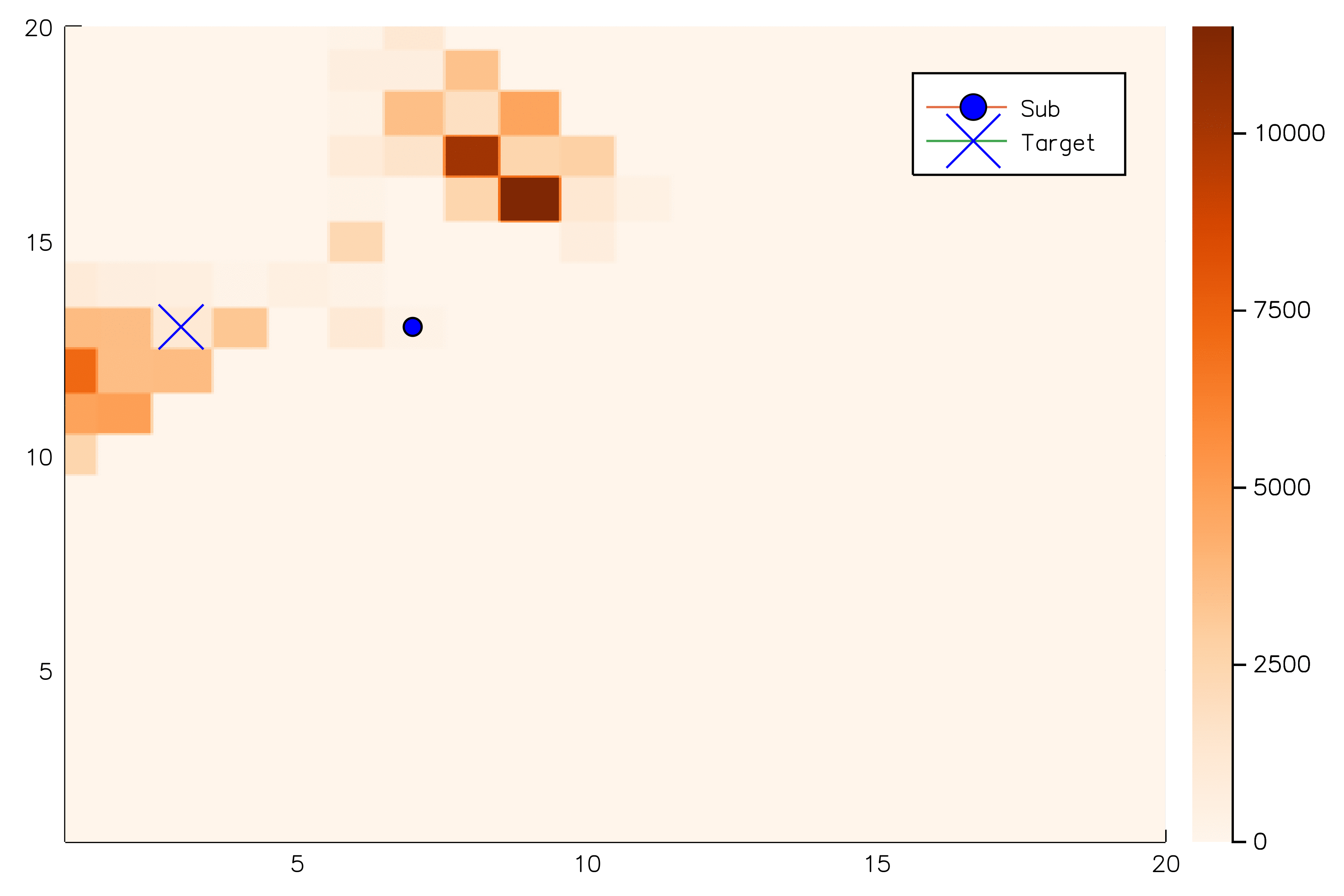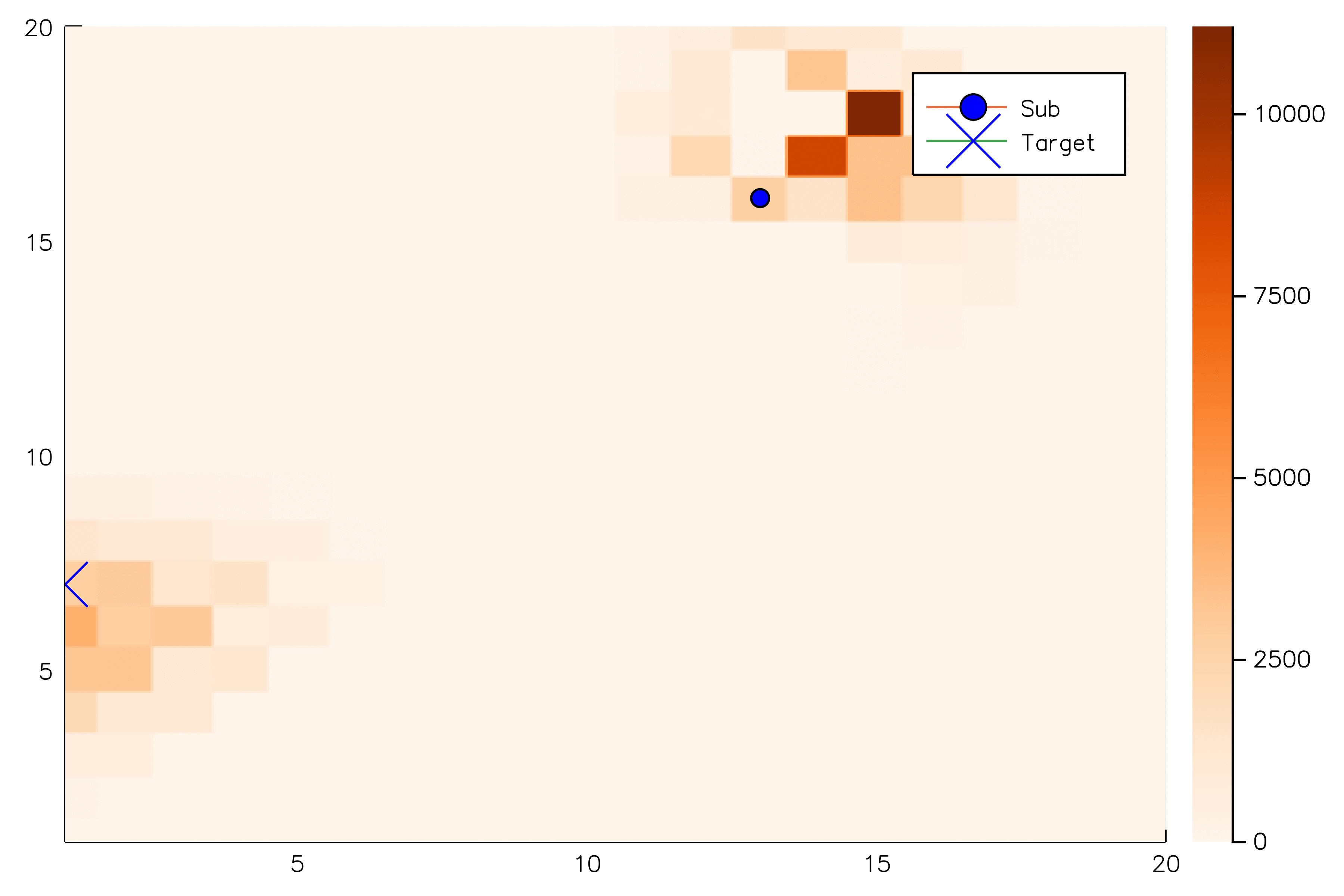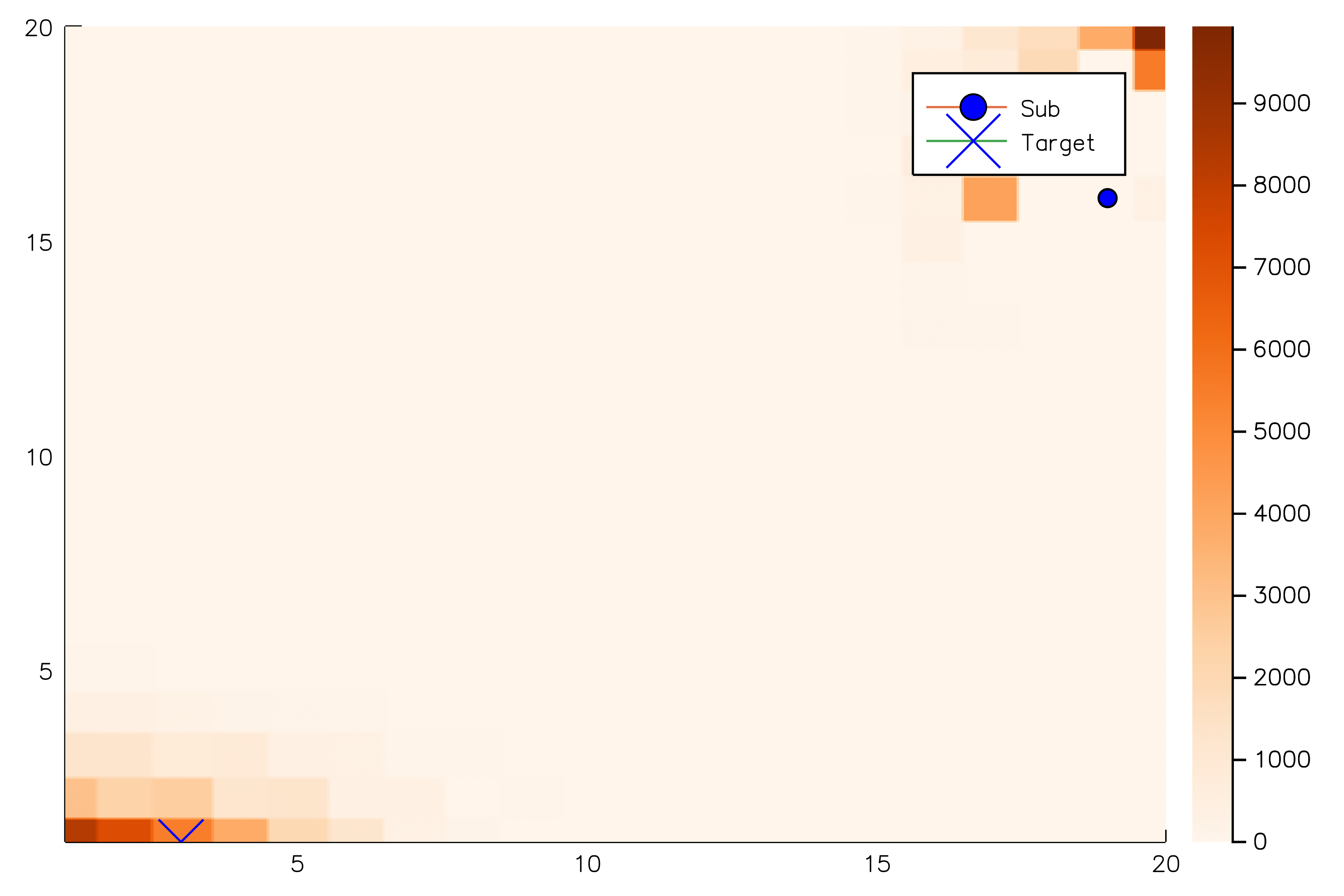
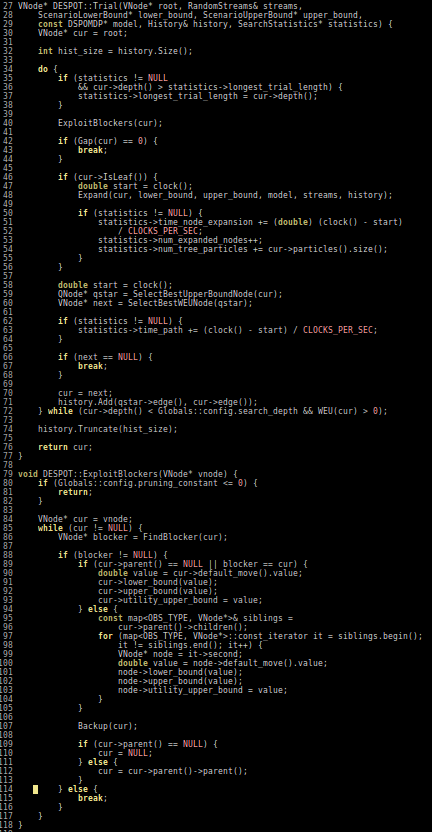
Solving continuous POMDPs - POMCP fails

[1] Adrien Coutoux, Jean-Baptiste Hoock, Nataliya Sokolovska, Olivier Teytaud, Nicolas Bonnard. Continuous Upper Confidence Trees. LION’11: Proceedings of the 5th International Conference on Learning and Intelligent OptimizatioN, Jan 2011, Italy. pp.TBA. <hal-00542673v2>

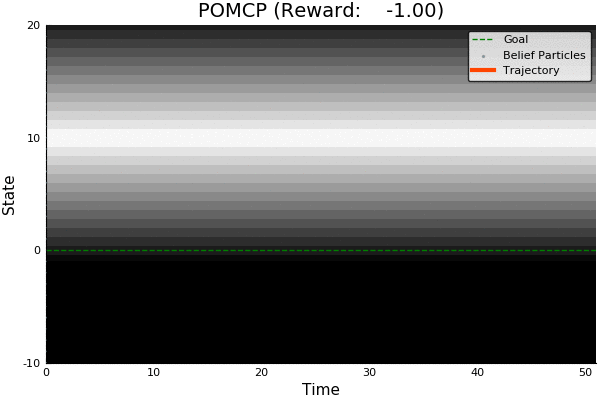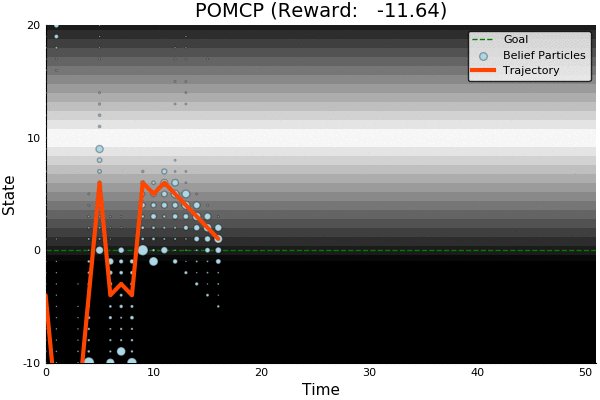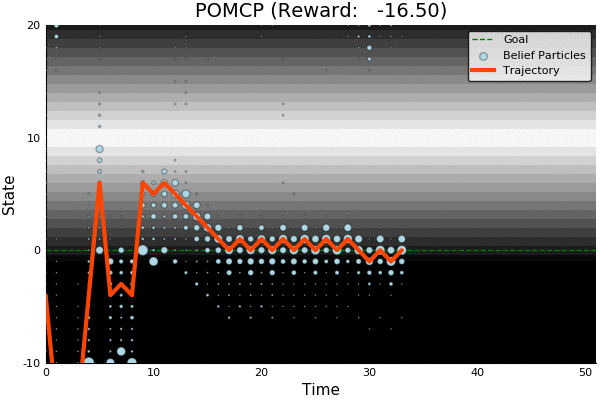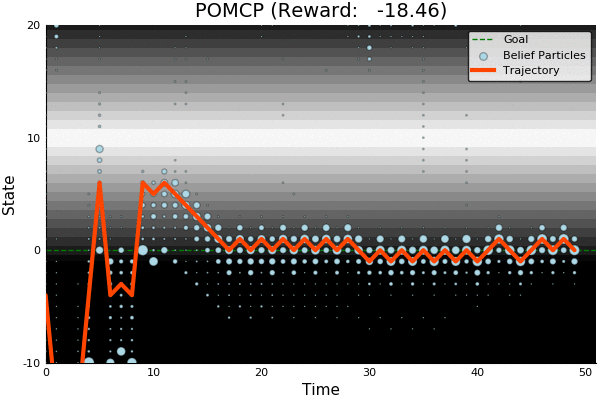
POMCP

✔

Limit number of children to

\[k N^\alpha\]

Necessary Conditions for Consistency [1]

POMCP

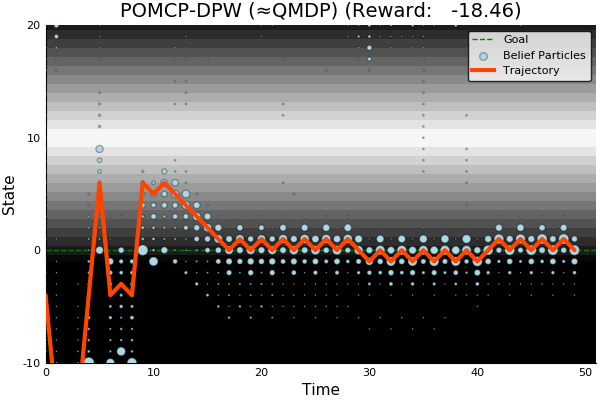
POMCP-DPW

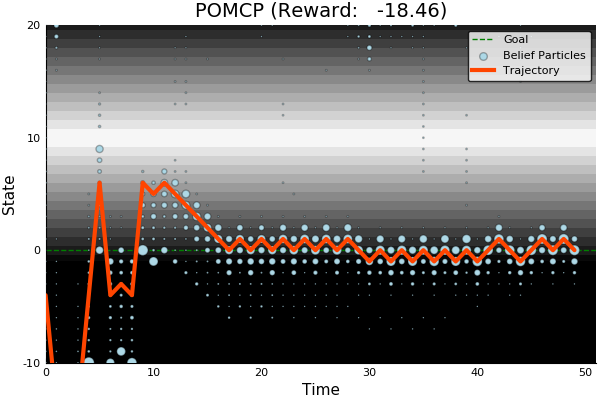
POMCP-DPW converges to QMDP

Proof Outline:

Observation space is continuous → observations unique w.p. 1.

(1) → One state particle in each belief, so each belief is merely an alias for that state

(2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state

Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP

Sunberg, Z. N. and Kochenderfer, M. J. "Online Algorithms for POMDPs with Continuous State, Action, and Observation Spaces", ICAPS (2018)

POMCP-DPW

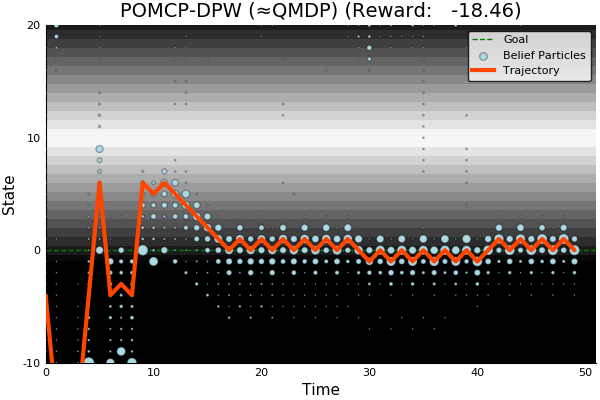
[ ] An infinite number of child nodes must be visited

[ ] Each node must be visited an infinite number of times

[ ] An infinite number of particles must be added to each belief node

✔

Necessary Conditions for Consistency

Use $Z$ to insert weighted particles

✔

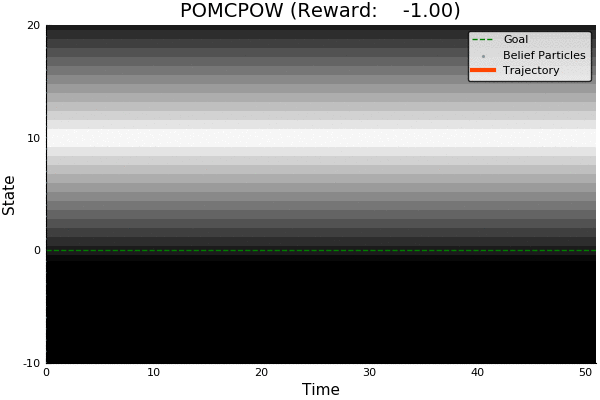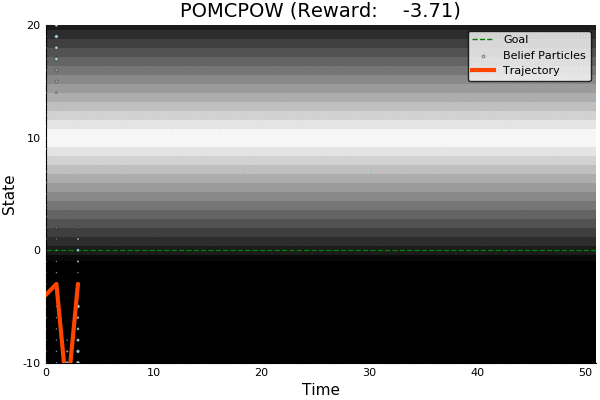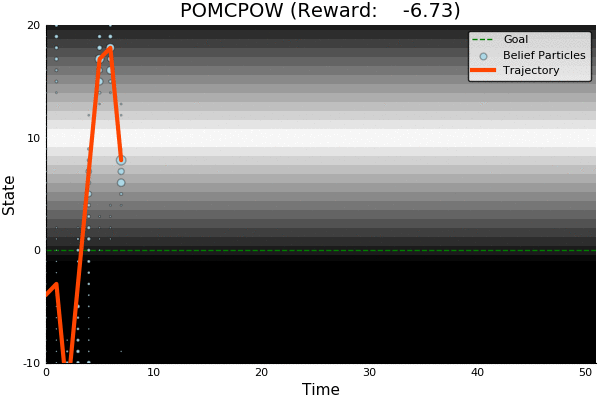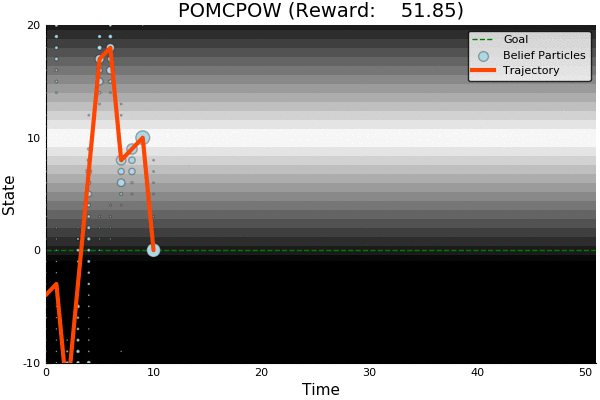
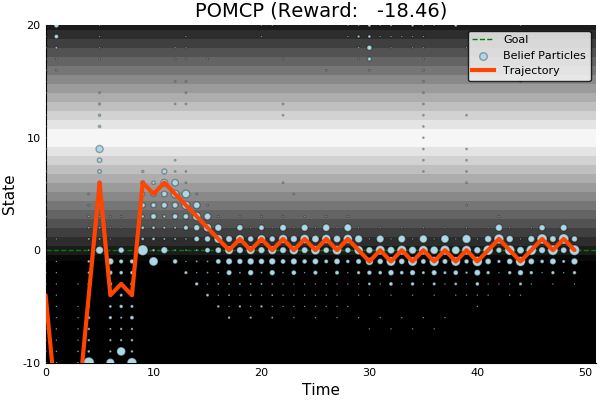
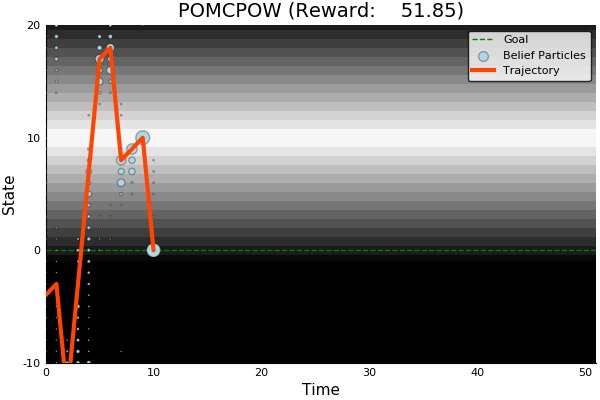
POMCP

POMCP-DPW

POMCPOW

Ye, Nan, et al. "DESPOT: Online POMDP planning with regularization." Journal of Artificial Intelligence Research 58 (2017): 231-266.

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

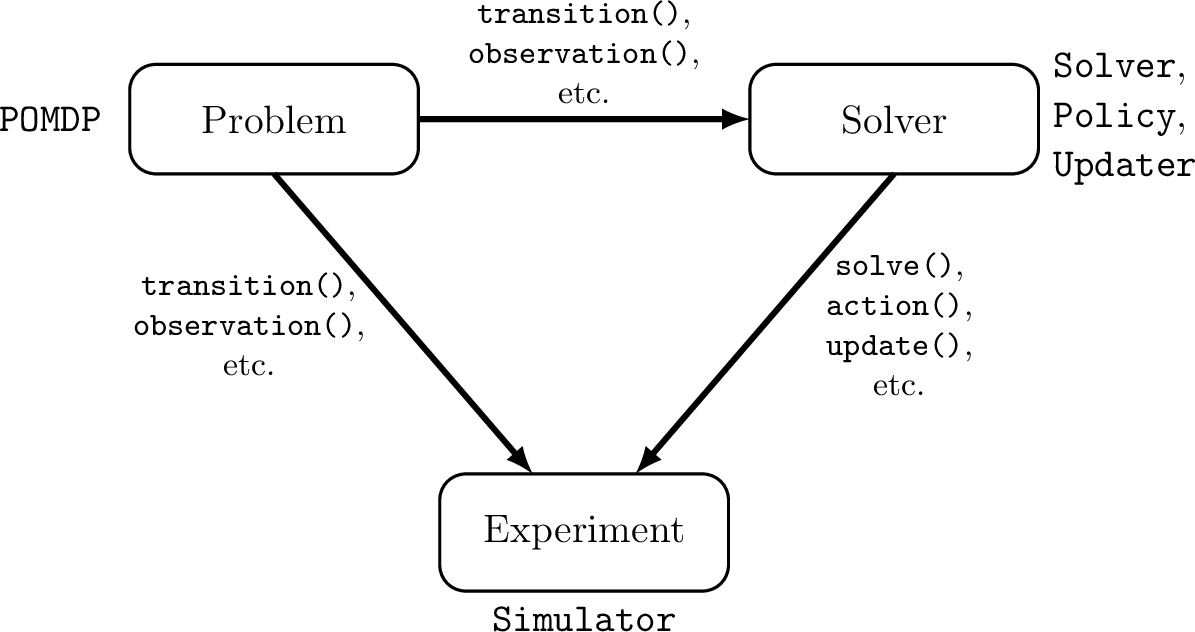
POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

Challenges for POMDP Software

POMDPs are computationally difficult.
There is a huge variety of
- Problems
  - Continuous/Discrete
  - Fully/Partially Observable
  - Generative/Explicit
  - Simple/Complex
- Solvers
  - Online/Offline
  - Alpha Vector/Graph/Tree
  - Exact/Approximate
- Domain-specific heuristics

Explicit

Generative

$s,a$

$s', o, r$

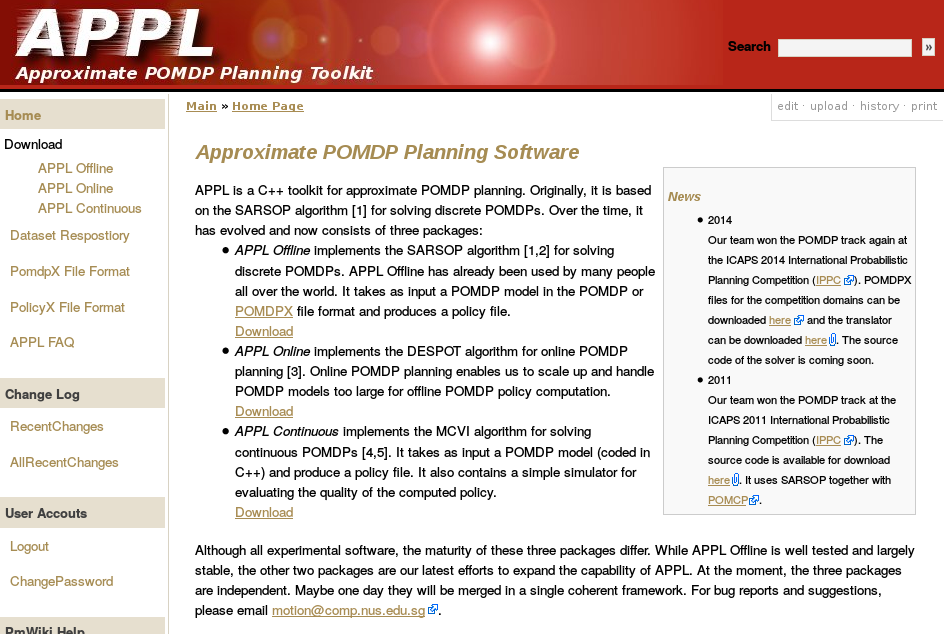
Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

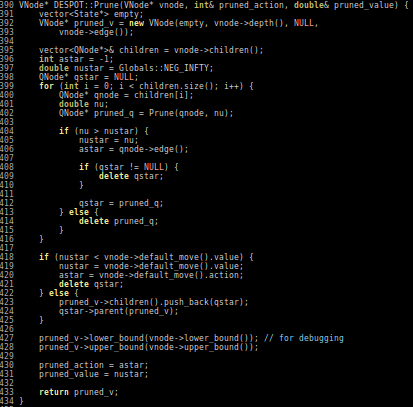
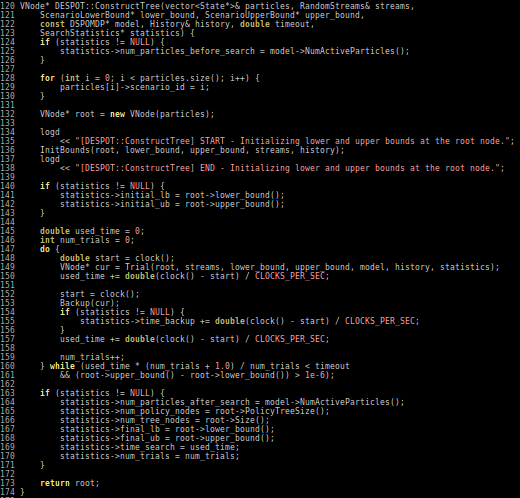
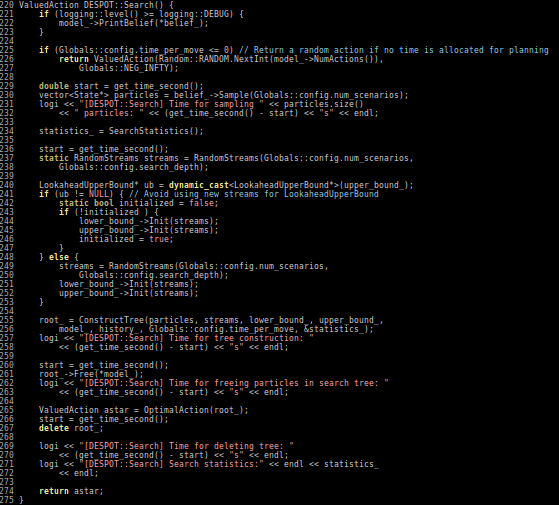
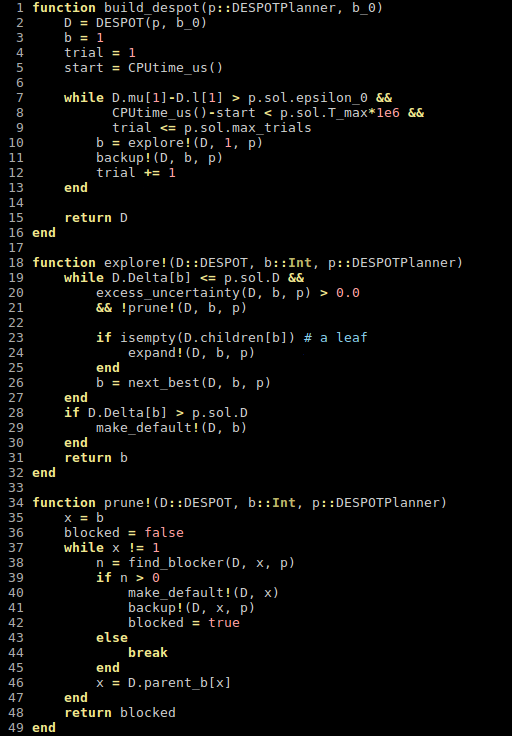
Conclusions

Solving UAV collision avoidance problems as MDPs offline offers safety an efficiency improvements even when combined with conservative safety constraints

In a simplified highway lane-changing scenario, there is a significant performance gap caused by ignoring the internal states of other drivers

This gap can be largely closed using POMDP planning

Current online POMDP solvers and naive double progressive widening are unable to solve POMDPs with continuous observation spaces that require costly exploration

POMCPOW and PFT-DPW are the first algorithms to obtain better-than-QMDP performance on such problems

POMDPs.jl provides a fast and easy to use framework for POMDP research and education

Peer-Reviewed Publications

Future Work

Investigate the effects of communication in lane changing with turn signals, "nudging in", etc. in highway lane changing
Test POMDP lane change planners on driver models learned from real data
Apply to internal-state-aware planning to simpler situations and test with real vehicles

Extend DESPOT to handle continuous POMDPs
Search for theoretical guarantees about the convergence of online continuous POMDP algorithms
Thoroughly investigate parallelism in online continuous POMDP algorithms