Safety and Efficiency in Autonomous Vehicles through Planning with Uncertainty

Zachary Sunberg

September 18, 2018

Indeed

San Francisco, CA

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

Autonomous Cars have a Challenge

Controlling an Autonomous Vehicle is inherently a multi-objective problem

EFFICIENCY

SAFETY

Minimize resource use

(especially time)

Minimize the risk of harm to oneself and others

Two extremes:

Optimization Problem

Safety

Better Performance

Model \(M_2\), Algorithm \(A_2\)

Model \(M_1\), Algorithm \(A_1\)

Efficiency

$$\text{maximize} \quad J = J_\text{E} + \lambda\, J_\text{S}$$

Safety

Weight

Efficiency

Markov Model

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}\) - Transition probability distributions

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward

Policy: \(\pi : \mathcal{S} \to \mathcal{A}\)

Maps every state to an action.

The Value Function

Reward: \(R(s_t, a_t)\)

Value: \(V_\pi(s) =E\left[\sum_{t=0}^\infty R(s_t, a_t)\right]\)

Solving MDPs and POMDPs - The Value Function

$$\mathop{\text{maximize}} V_\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, \pi(s_t)) \bigm| s_0 = s \right]$$

$$V^*(s) = \max \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$

\pi: \mathcal{S} \to \mathcal{A}
π:S→A\pi: \mathcal{S} \to \mathcal{A}

Involves all future time

Involves only \(t\) and \(t+1\)

\(a \in \mathcal{A}\)

Online Decision Process Tree Approaches

State Node

Action Node

(Estimate value function here)

Monte Carlo Tree Search

Image by Dicksonlaw583 (CC 4.0)

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward

Types of Uncertainty

OUTCOME

MODEL

STATE

Partially Observable Markov Decision Process (POMDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward
  • \(\mathcal{O}\) - Observation space
  • \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution

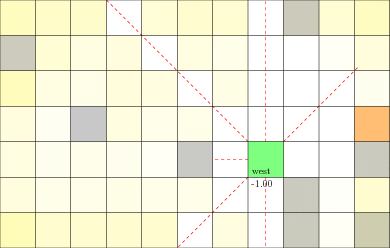
Laser Tag Example

Belief

History: all previous actions and observations

\[h_t = (b_0, a_0, o_1, a_1, o_2, ..., a_{t-1}, o_t)\]

Belief: probability distribution over \(\mathcal{S}\) encoding everything learned about the state from the history

\[b_t(s) = P(s_t=s \mid h_t)\]

A POMDP is an MDP on the belief space

C. H. Papadimitriou and J. N. Tsitsiklis, “The complexity of Markov decision processes,” Mathematics of Operations Research, vol. 12, no. 3, pp. 441–450, 1987

But POMDPs are PSPACE-Complete

Sadigh, Dorsa, et al. "Information gathering actions over human internal state." Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference on. IEEE, 2016.

Schmerling, Edward, et al. "Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction." arXiv preprint arXiv:1710.09483 (2017).

Sadigh, Dorsa, et al. "Planning for Autonomous Cars that Leverage Effects on Human Actions." Robotics: Science and Systems. 2016.

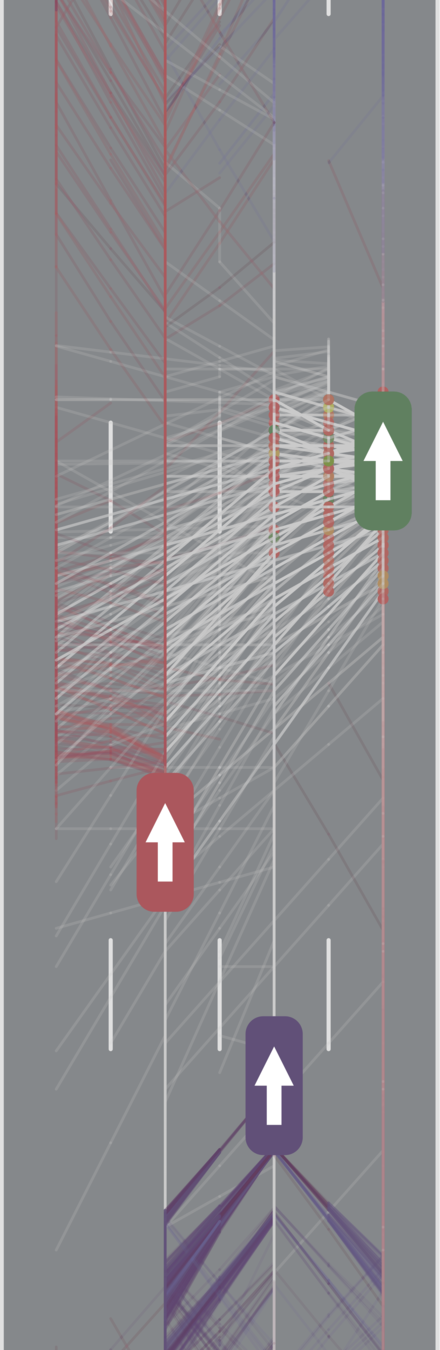
Lane Change Planning with

Internal States

Human Behavior Model: IDM and MOBIL

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
x¨IDM=a[1−(x˙x˙0)δ−(g∗(x˙,Δx˙)g)2] \ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}
g∗(x˙,Δx˙)=g0+Tx˙+x˙Δx˙2abg^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).

A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).

A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).

MDP Formulation

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c\phantom{, \theta_c})\right\}_{c=1}^{n}\right)\)

 

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

Ego physical state

Physical states of other cars

  • Actions filtered so they can never cause crashes
  • Braking action always available

Efficiency

Safety

\[R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)\]

POMDP Formulation

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1 \text{ m/s}^2\}\), \(\dot{y} \in \{0, \pm 0.67 \text{ m/s}\}\)

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states of other cars

  • Actions filtered so they can never cause crashes
  • Braking action always available

Efficiency

Safety

\[R(s, a, s') = \text{in\_goal}(s') - \lambda \left(\text{any\_hard\_brakes}(s, s') + \text{any\_too\_slow}(s')\right)\]

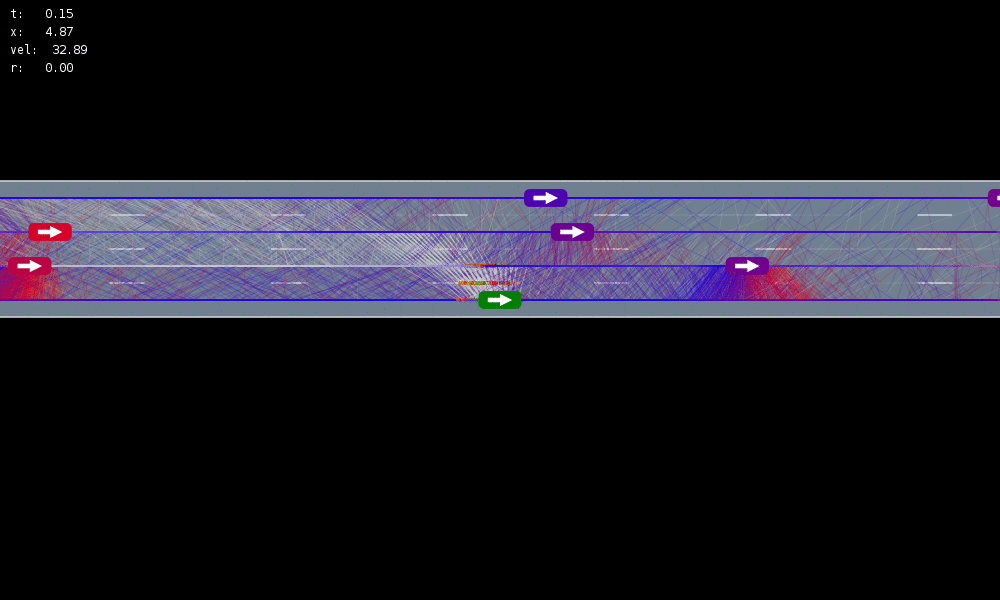
All drivers normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Simulation results

Assume normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Correlation Trend

Robustness

Future Work

Thank You!

Find out more at

zachary.sunberg.net

Work sponsored by

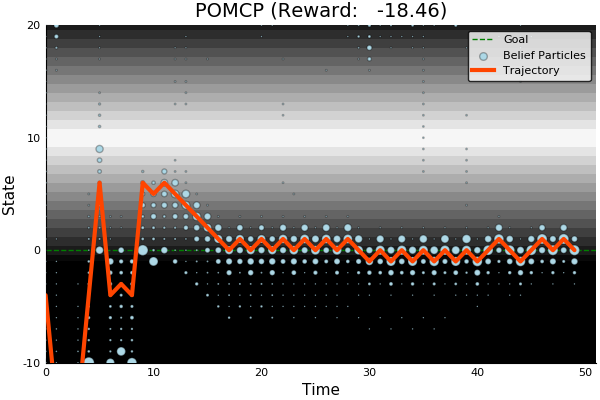
POMCP

  • Uses simulations of histories instead of full belief updates

 

  • Each belief is implicitly represented by a collection of unweighted particles

 

Silver, David, and Joel Veness. "Monte-Carlo planning in large POMDPs." Advances in neural information processing systems. 2010.

Ross, Stéphane, et al. "Online planning algorithms for POMDPs." Journal of Artificial Intelligence Research 32 (2008): 663-704.

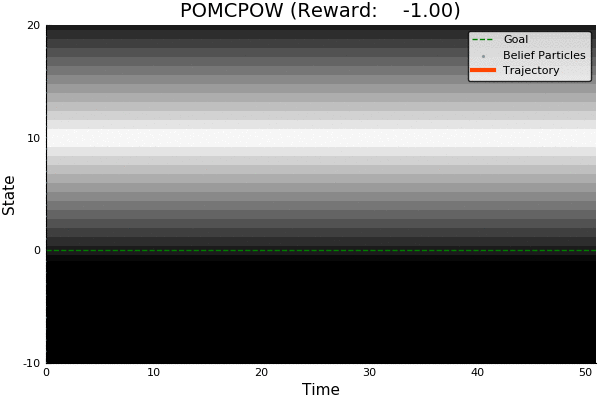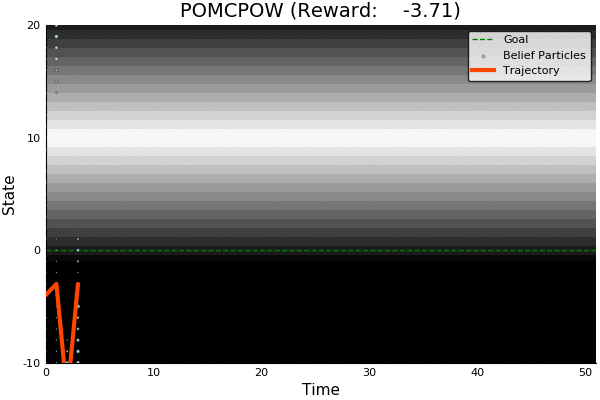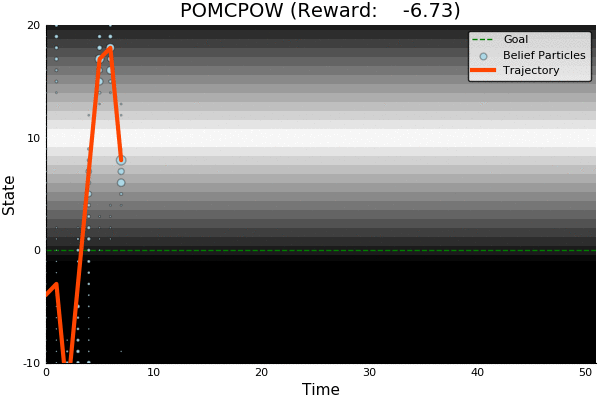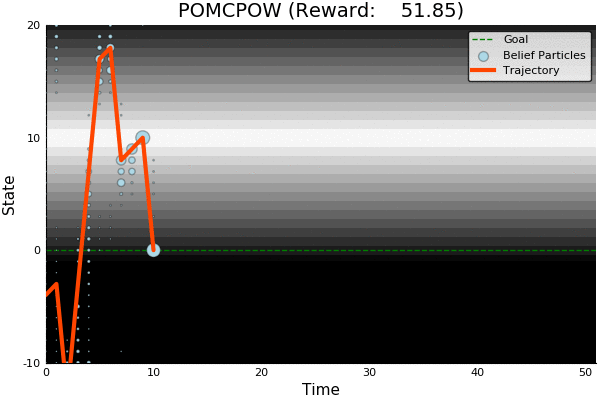
Light-Dark Problem

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}
S=Z  O=Rs′=s+ao∼N(s,s−10)A={−10,−1,0,1,10}R(s,a)={100 if a=0,s=0−100 if a=0,s≠0−1 otherwise\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

Goal: \(a=0\) at \(s=0\)

Optimal Policy

Localize

\(a=0\)

 

[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

Solving continuous POMDPs - POMCP fails

[1] Adrien Coutoux, Jean-Baptiste Hoock, Nataliya Sokolovska, Olivier Teytaud, Nicolas Bonnard. Continuous Upper Confidence Trees. LION’11: Proceedings of the 5th International Conference on Learning and Intelligent OptimizatioN, Jan 2011, Italy. pp.TBA. <hal-00542673v2>

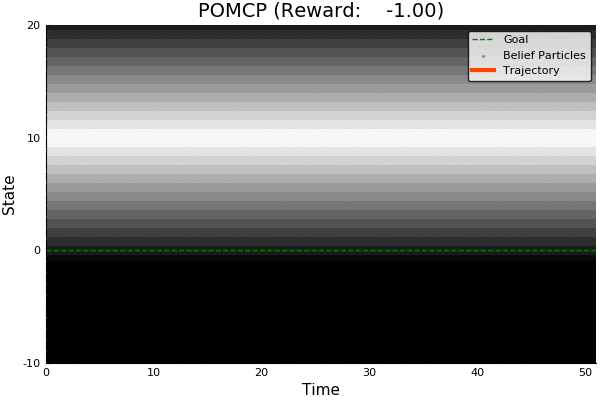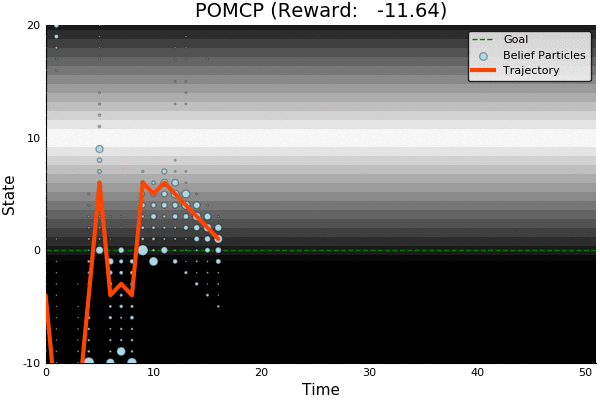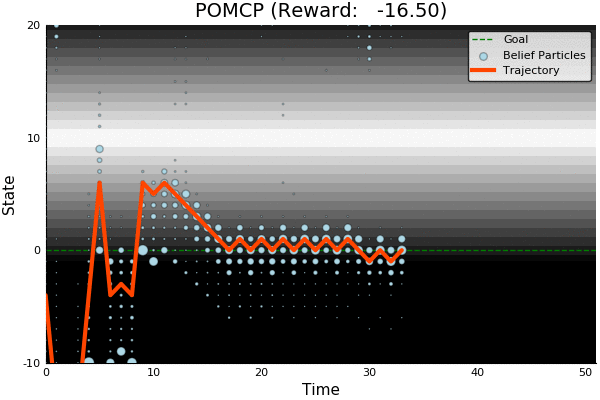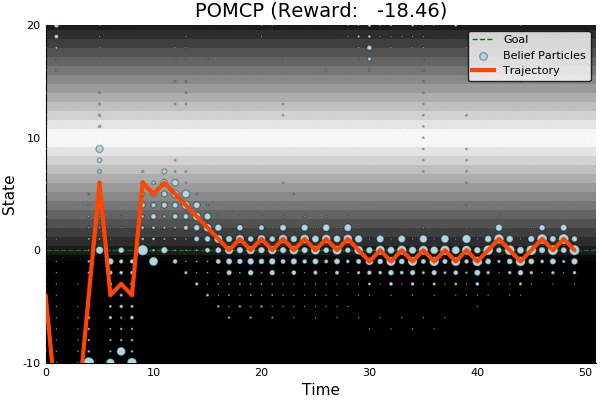
POMCP

✔

✔

Limit number of children to

\[k N^\alpha\]

Necessary Conditions for Consistency [1]

 

POMCP

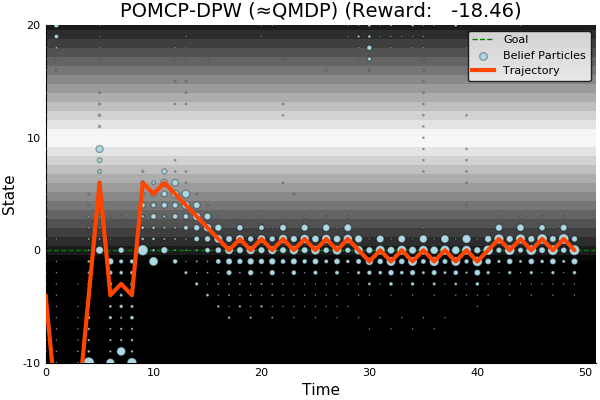
POMCP-DPW

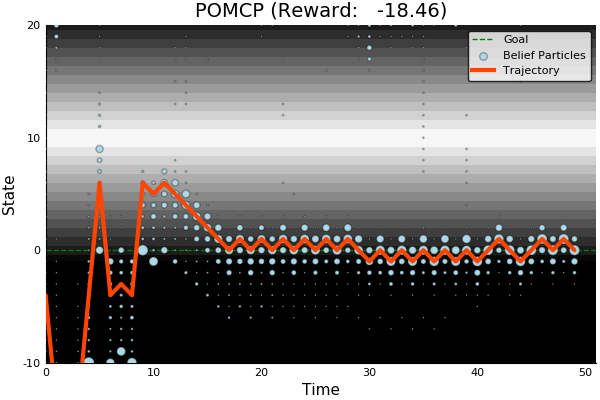
POMCP-DPW converges to QMDP

Proof Outline:

  1. Observation space is continuous → observations unique w.p. 1.


  2. (1) → One state particle in each belief, so each belief is merely an alias for that state


  3. (2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state


  4. Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP



    5.  

Sunberg, Z. N. and Kochenderfer, M. J. "Online Algorithms for POMDPs with Continuous State, Action, and Observation Spaces", ICAPS (2018)

POMCP-DPW

 

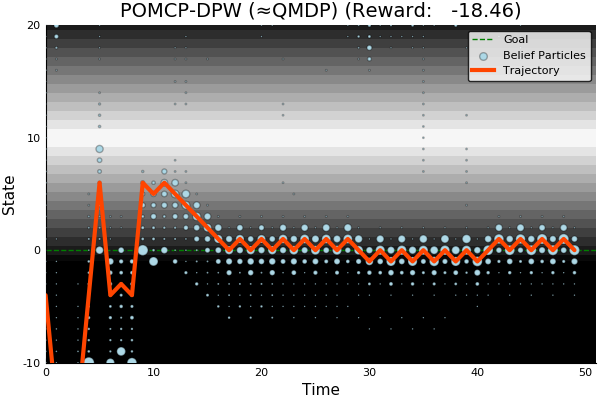
[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

[  ] An infinite number of particles must be added to each belief node

✔

✔

Necessary Conditions for Consistency

 

Use \(Z\) to insert weighted particles

✔

POMCP

POMCP-DPW

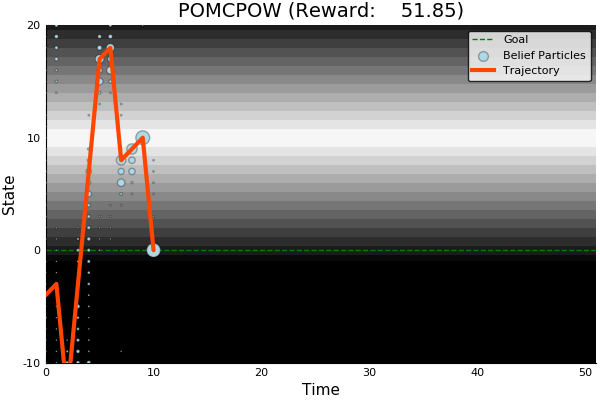
POMCPOW

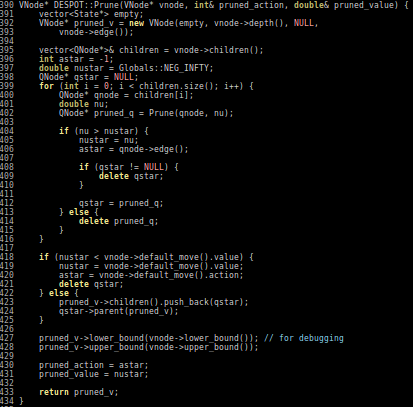
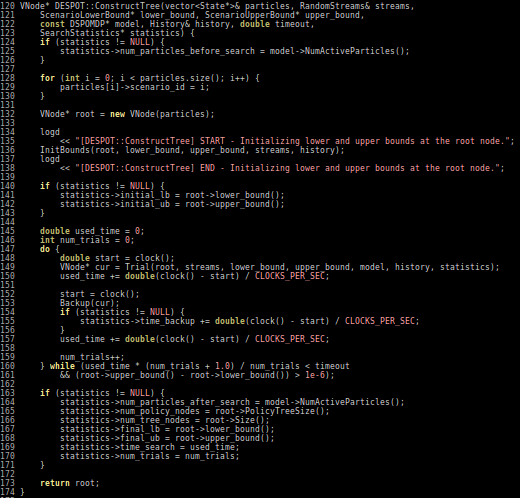
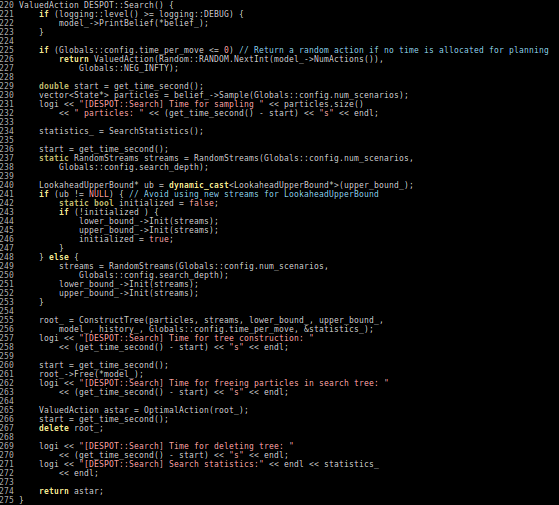
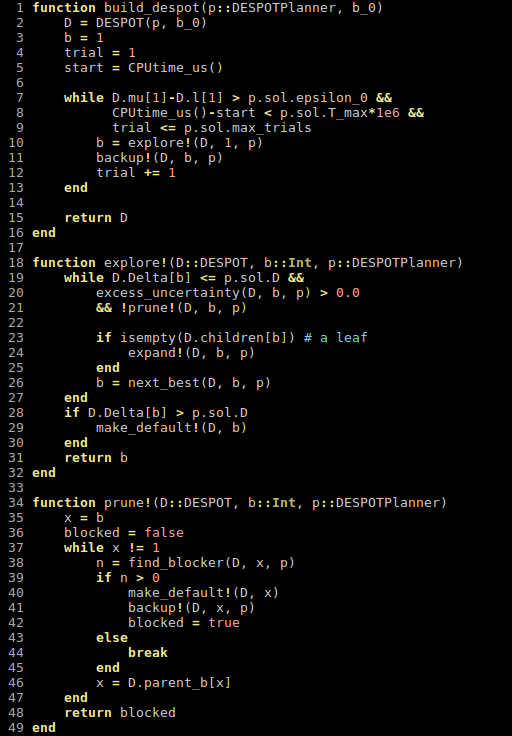
Ye, Nan, et al. "DESPOT: Online POMDP planning with regularization." Journal of Artificial Intelligence Research 58 (2017): 231-266.

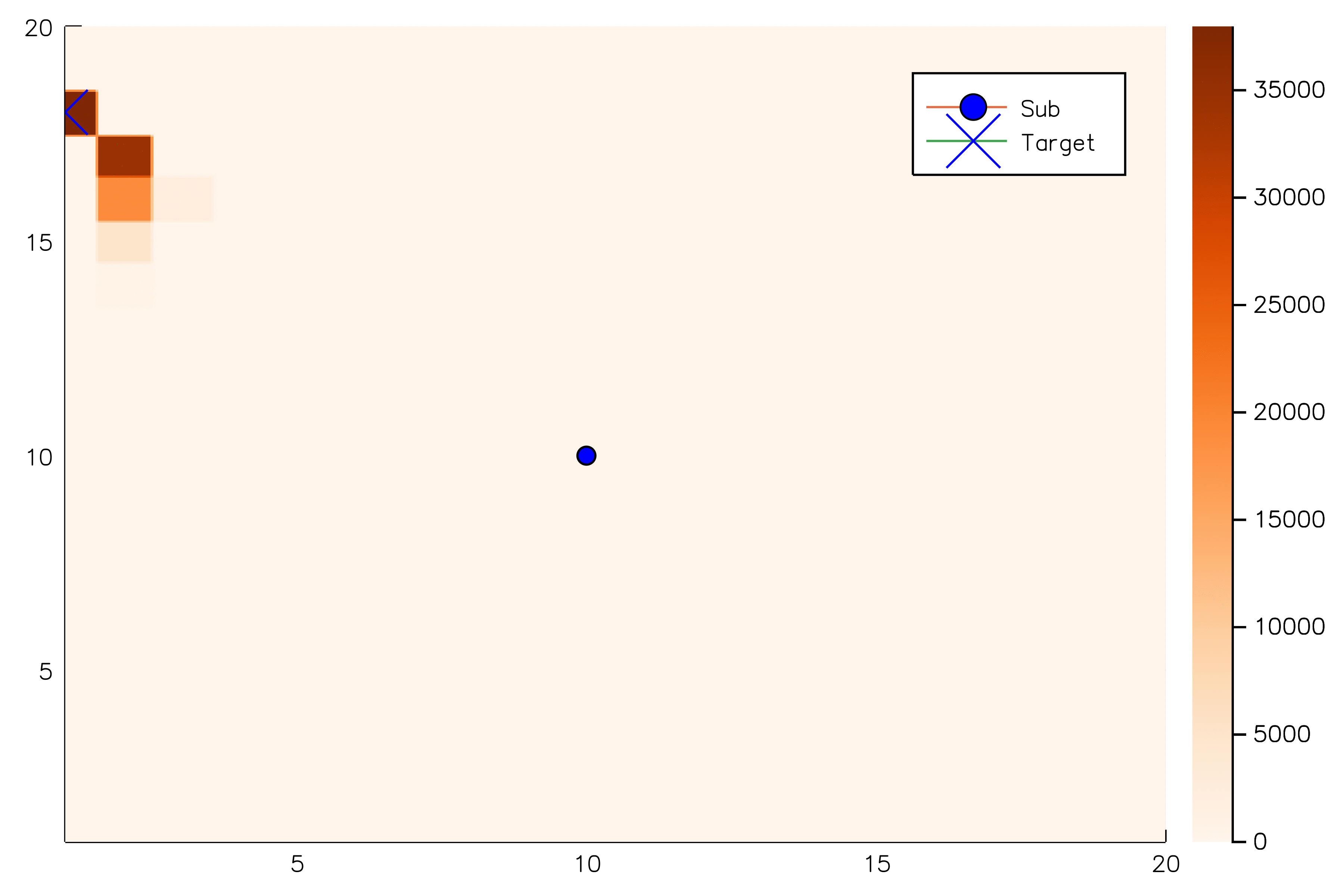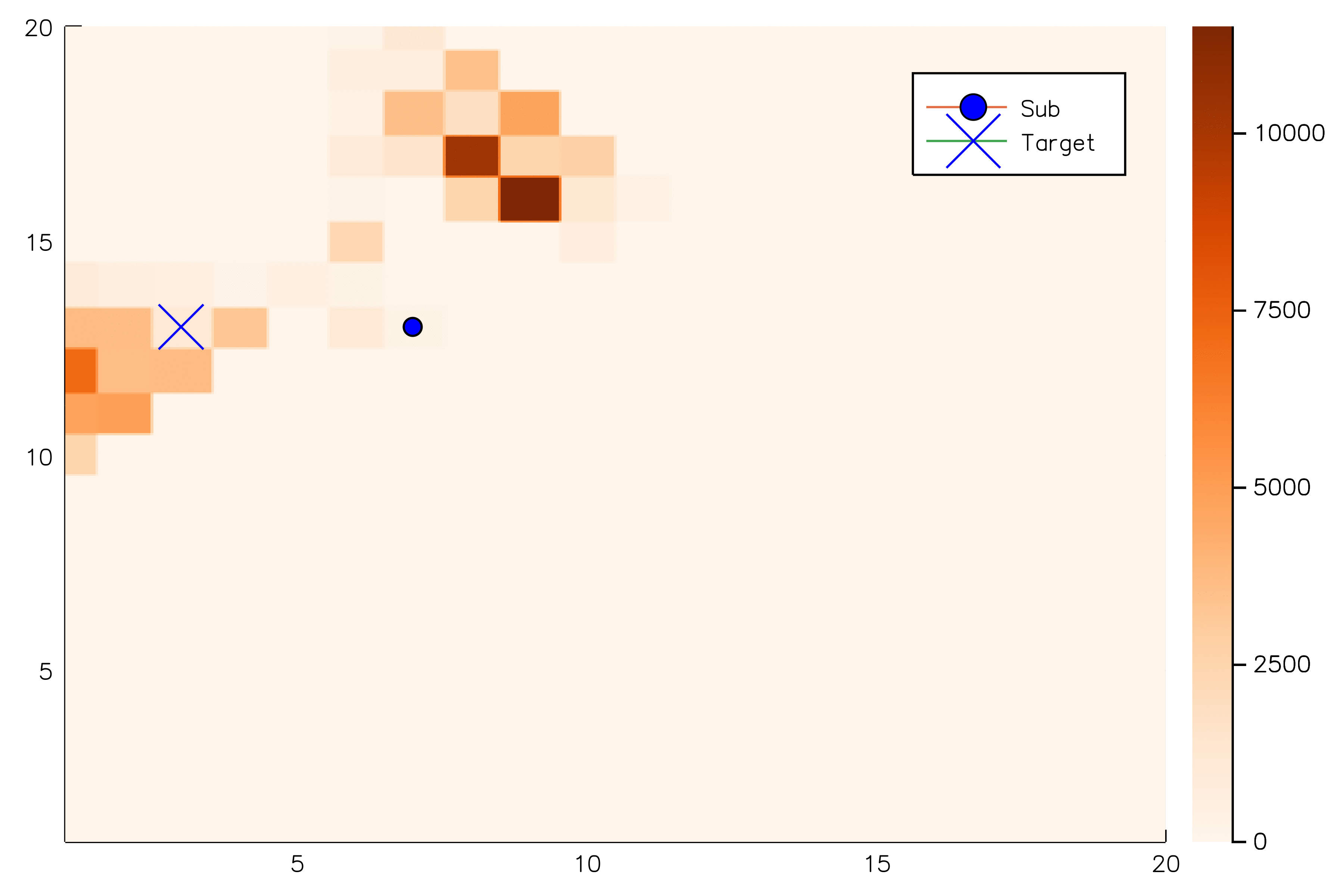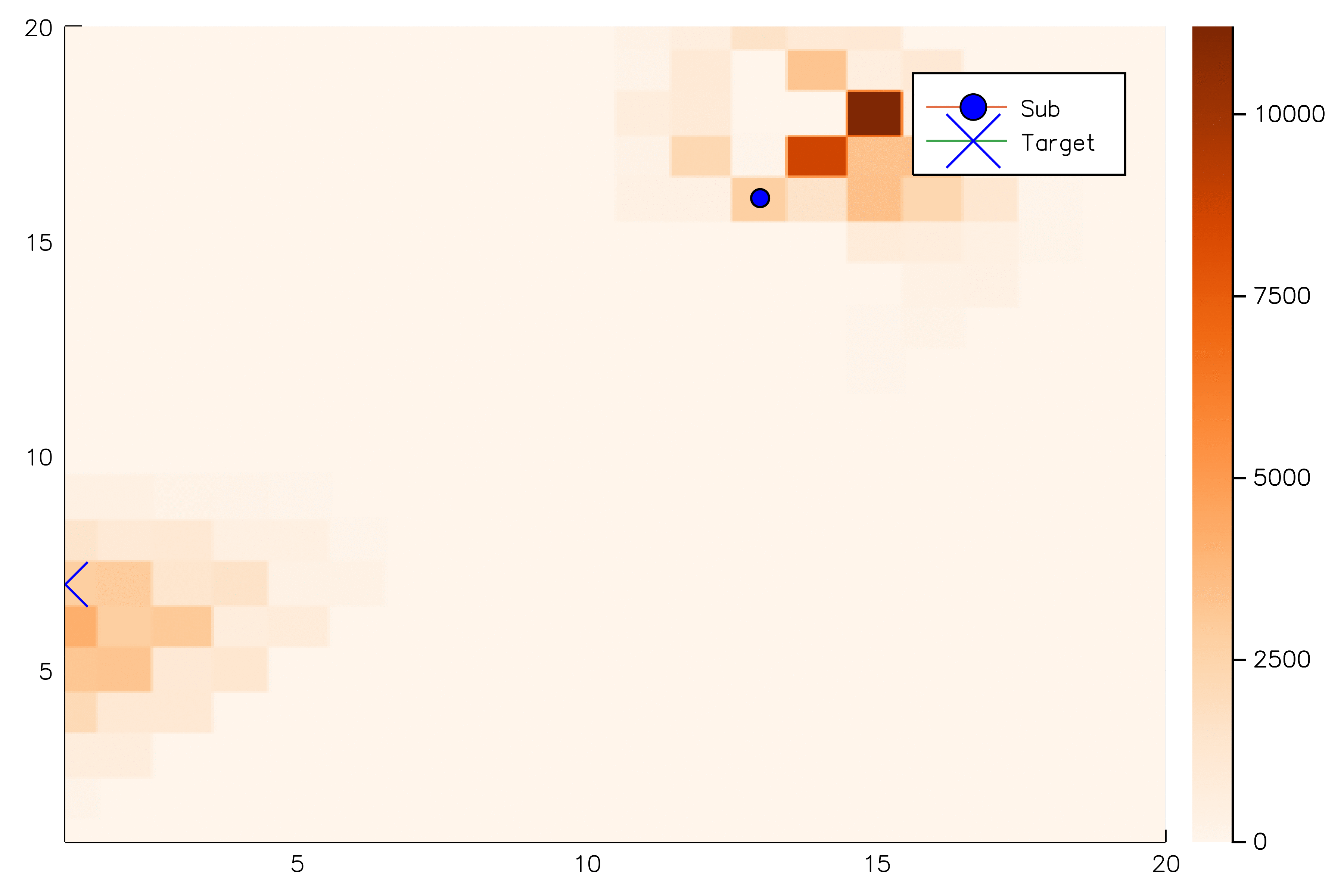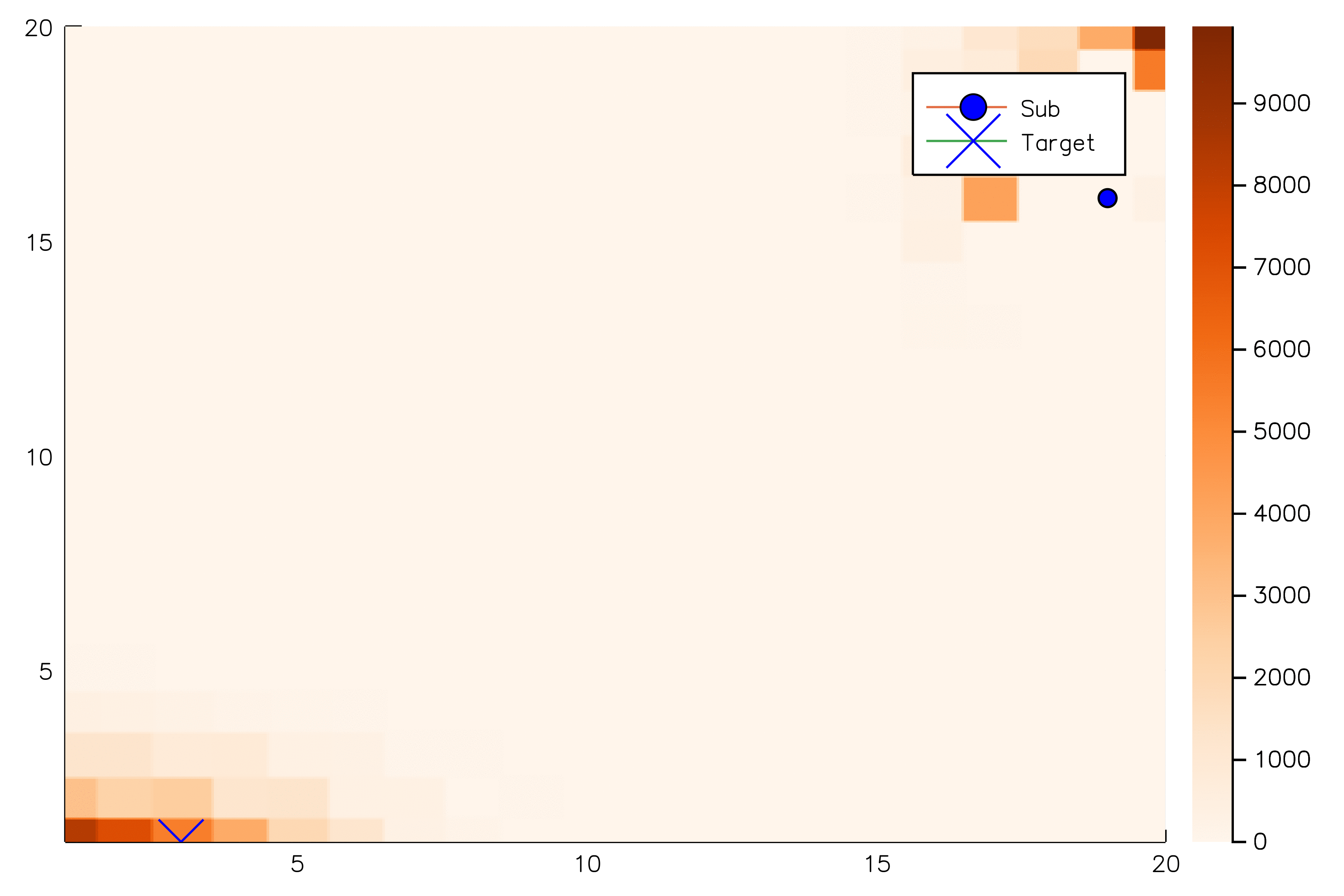
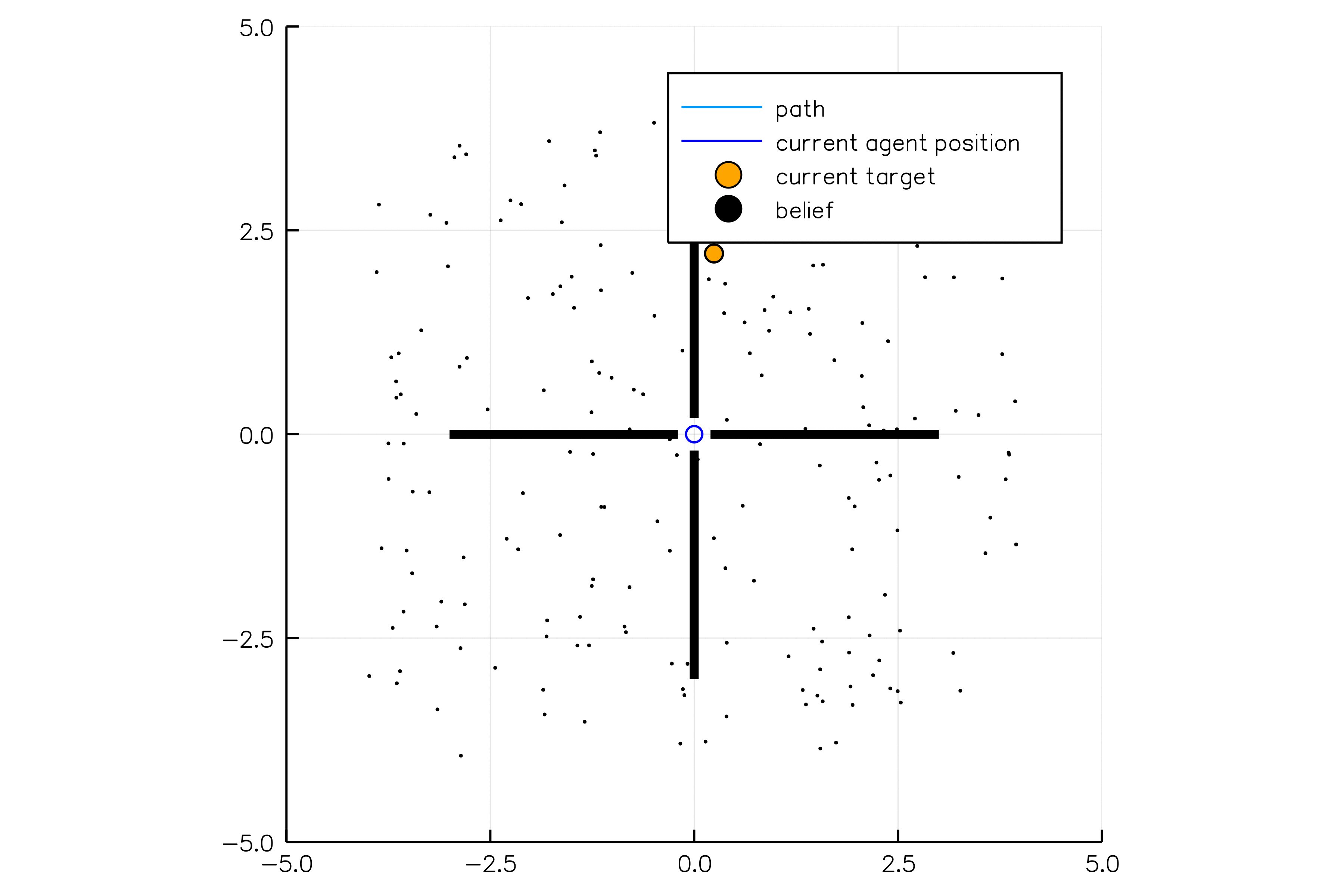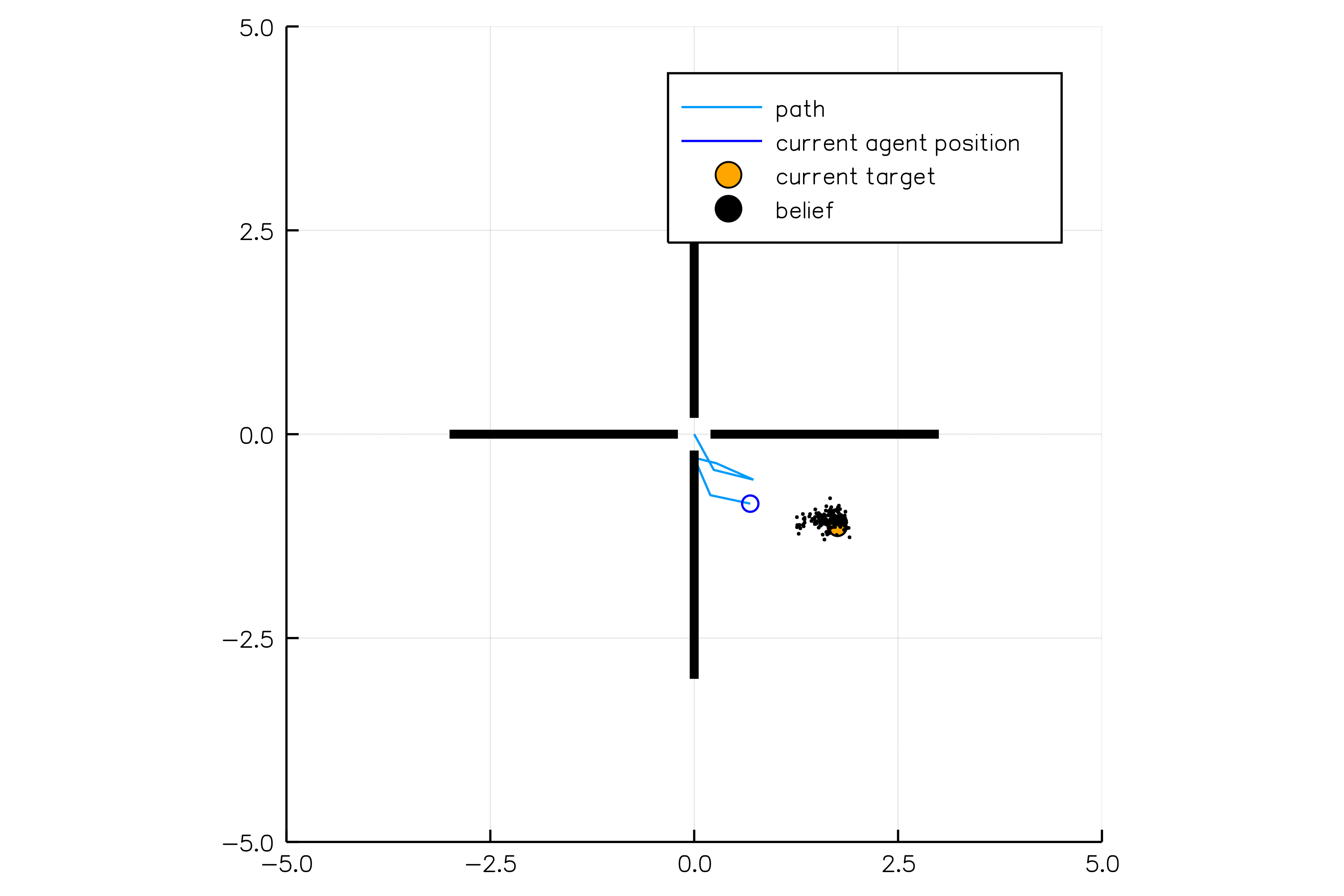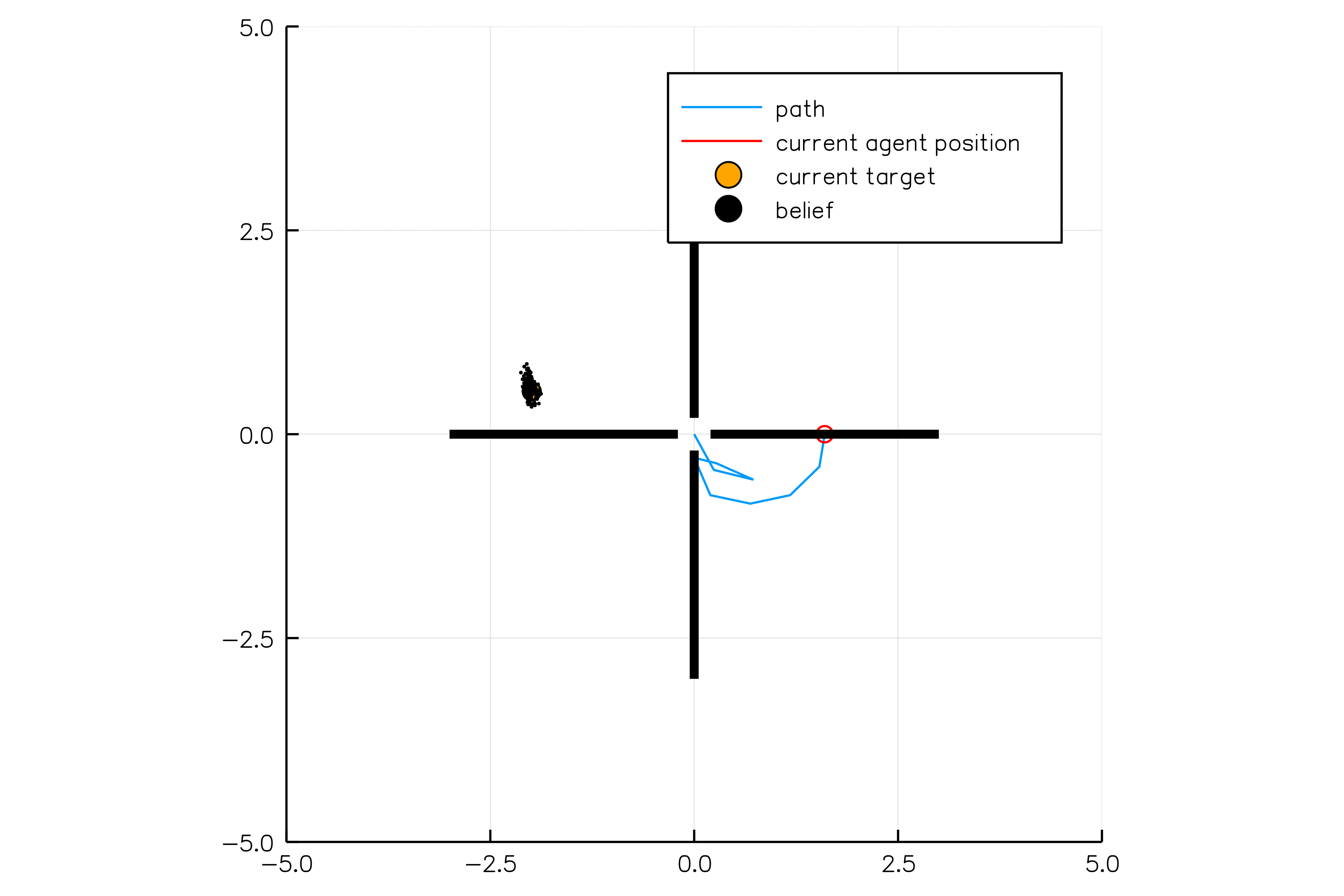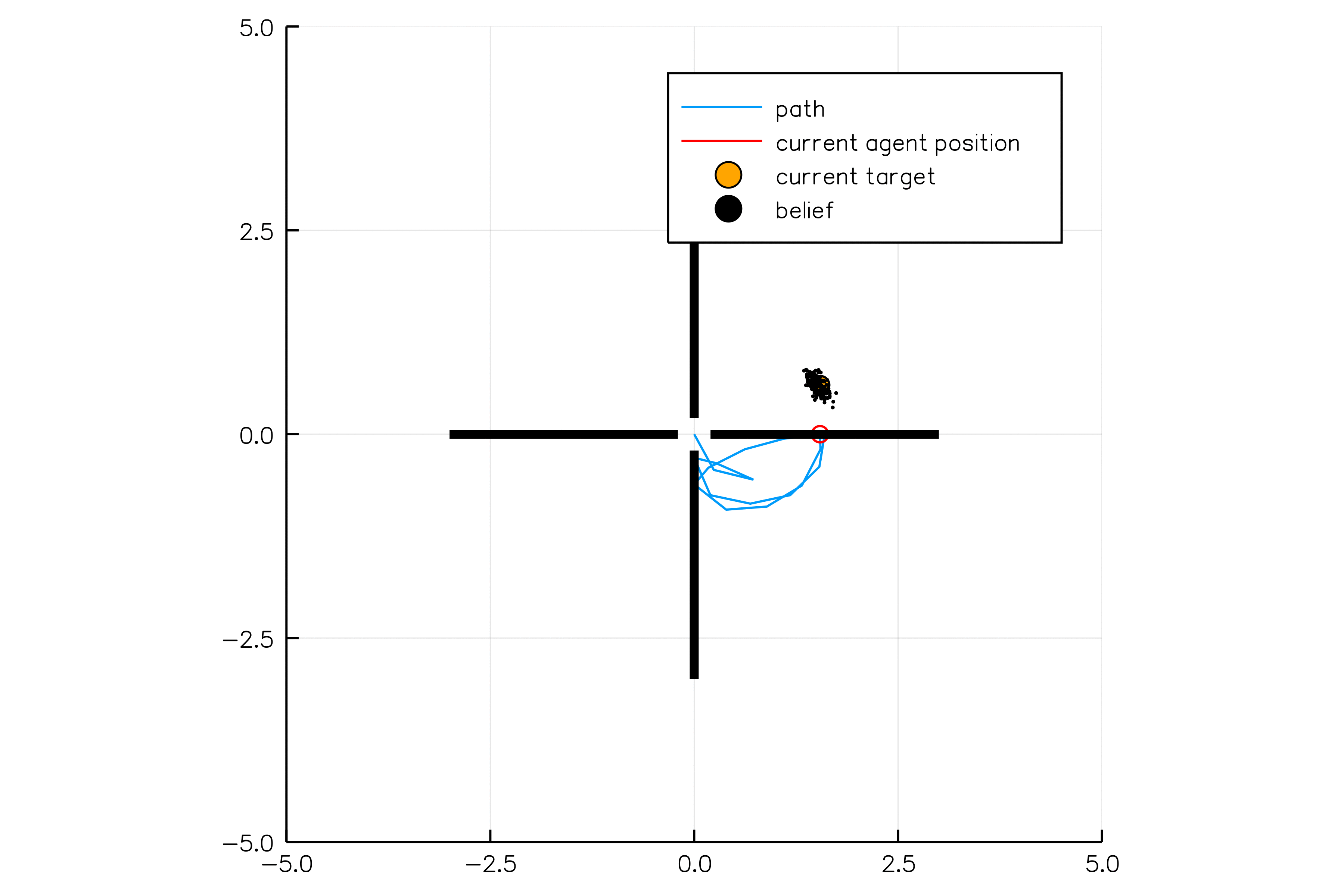
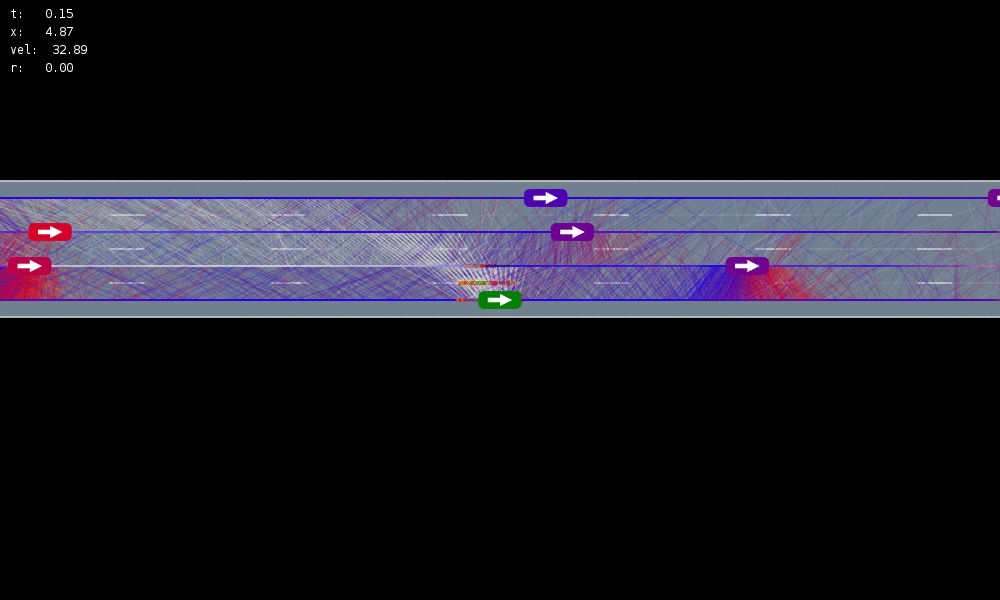
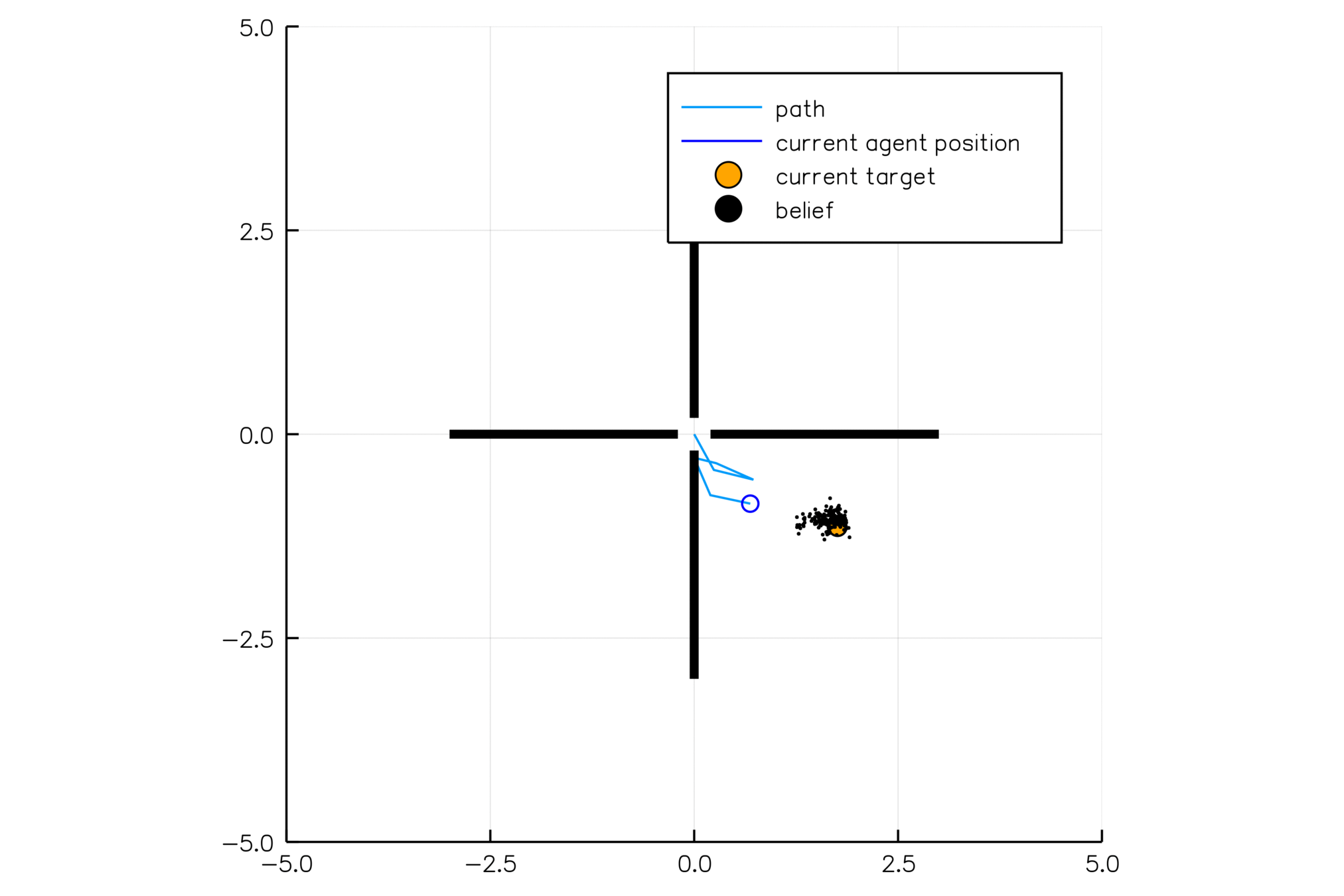
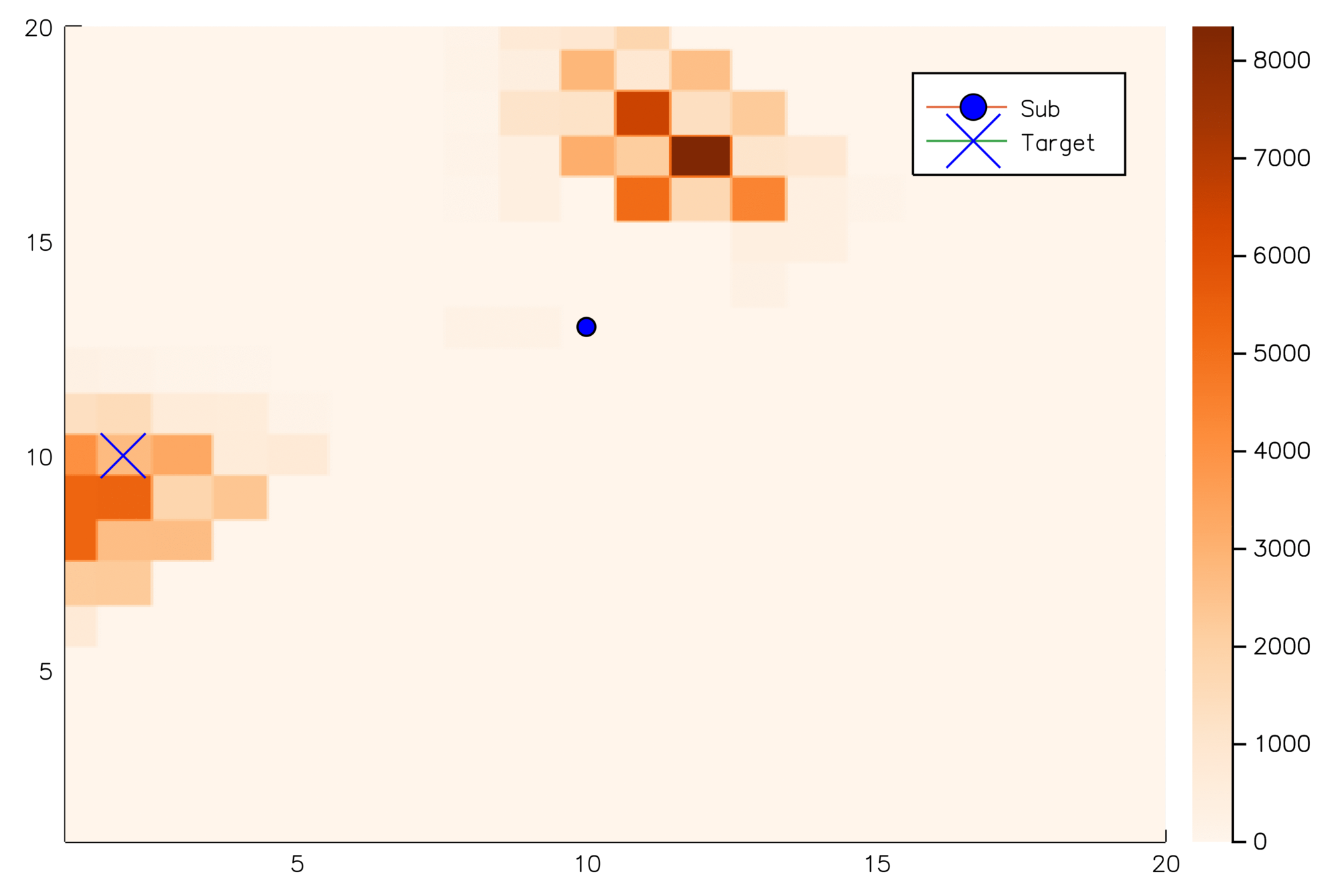
Future Work

(i.e. this month)

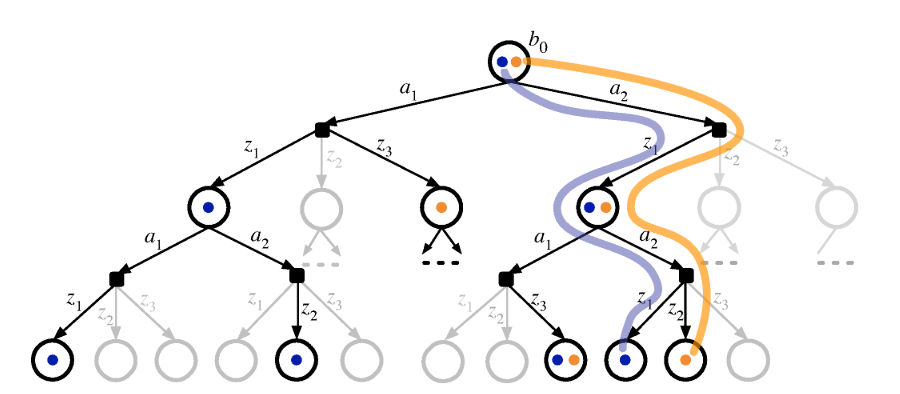
Extend to DESPOT

Ye, Nan, et al. "DESPOT: Online POMDP planning with regularization." Journal of Artificial Intelligence Research 58 (2017): 231-266.

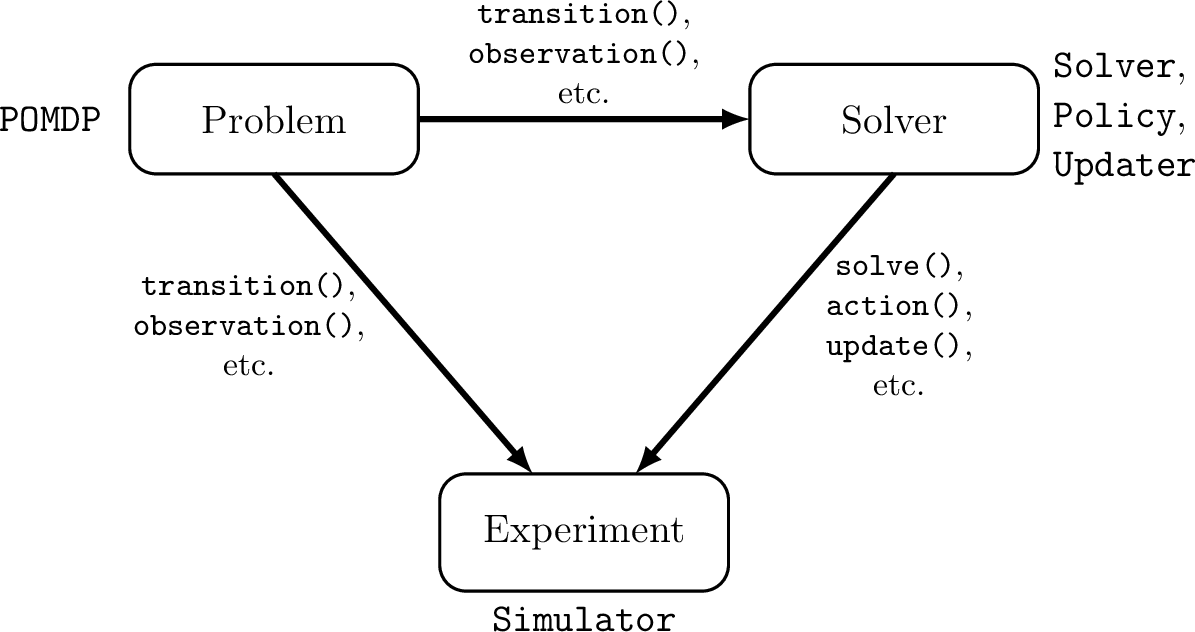
POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

Challenges for POMDP Software

  1. POMDPs are computationally difficult.
  2. There is a huge variety of
    • Problems
      • Continuous/Discrete
      • Fully/Partially Observable
      • Generative/Explicit
      • Simple/Complex
    • Solvers
      • Online/Offline
      • Alpha Vector/Graph/Tree
      • Exact/Approximate
    • Domain-specific heuristics

Julia - Speed

Challenges for POMDP Software

  1. POMDPs are computationally difficult.
  2. There is a huge variety of
    • Problems
      • Continuous/Discrete
      • Fully/Partially Observable
      • Generative/Explicit
      • Simple/Complex
    • Solvers
      • Online/Offline
      • Alpha Vector/Graph/Tree
      • Exact/Approximate
    • Domain-specific heuristics

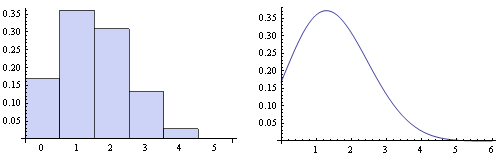
Explicit

Generative

\(s,a\)

\(s', o, r\)

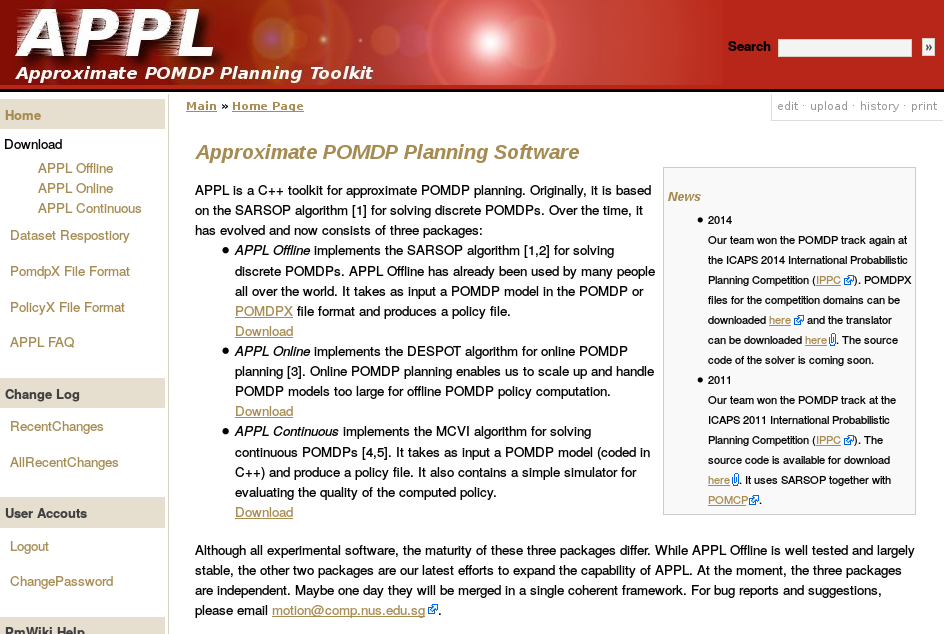
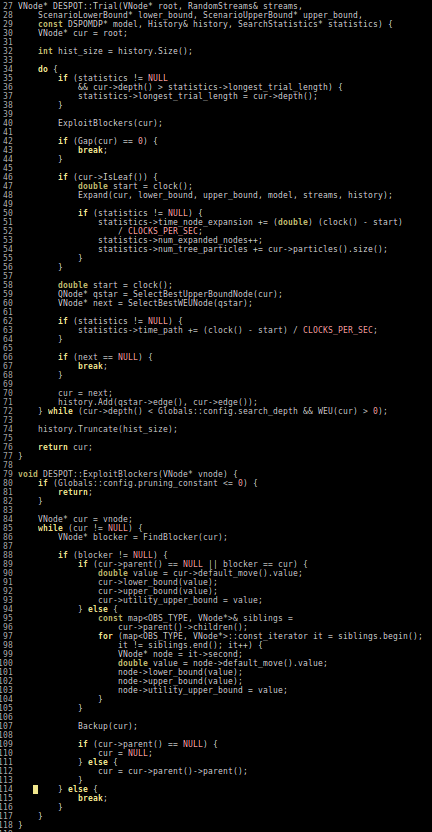
Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

Future Research

SAFE, EFFICIENT control for the

REAL WORLD

Two problems from Aerospace

Autorotation

Flight Tests

"Expert System" Autorotation Controller

Example Controller: Flare

 

\[\alpha \equiv \frac{KE_{\text{available}} - KE_{\text{flare exit}}}{KE_{\text{flare entry}} - KE_{\text{flare exit}}}\]

\[TTLE = TTLE_{max} \times \alpha\]

\[\ddot{h}_{des} = -\frac{2}{TTI_F^2}h - \frac{2}{TTI_F}\dot{h}\]

Bad because:

  • No optimality justification
  • Controller must be adjusted by hand to accommodate any changes
  • Difficult to communicate about
  • Parameters not intuitive

A better way: MPC Value Iteration

\(R\) quasi-convex (e.g. \(x_t \in \) safe landing)

Feasible sets convex

Energy Kites

  • Need safety guarantees
  • Every bit of efficiency is extra energy
  • Complex and partially observable dynamics
    • Aircraft dynamics
    • Tether state
    • Wind

Convex Optimization

Boyd, Stephen, and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.

Convexity <=> Exact Solution Tractable

all \(f\) convex

Indeed Talk

By Zachary Sunberg

Indeed Talk

  • 554

More from Zachary Sunberg