Safety and Efficiency for Autonomous Vehicles through Online Learning

Zachary Sunberg

Current: Postdoctoral Scholar, University of California

Future: Assistant Professor, University of Colorado

How do we deploy autonomy with confidence?

Safety and Efficiency through Online Learning

Waymo Image By Dllu - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=64517567

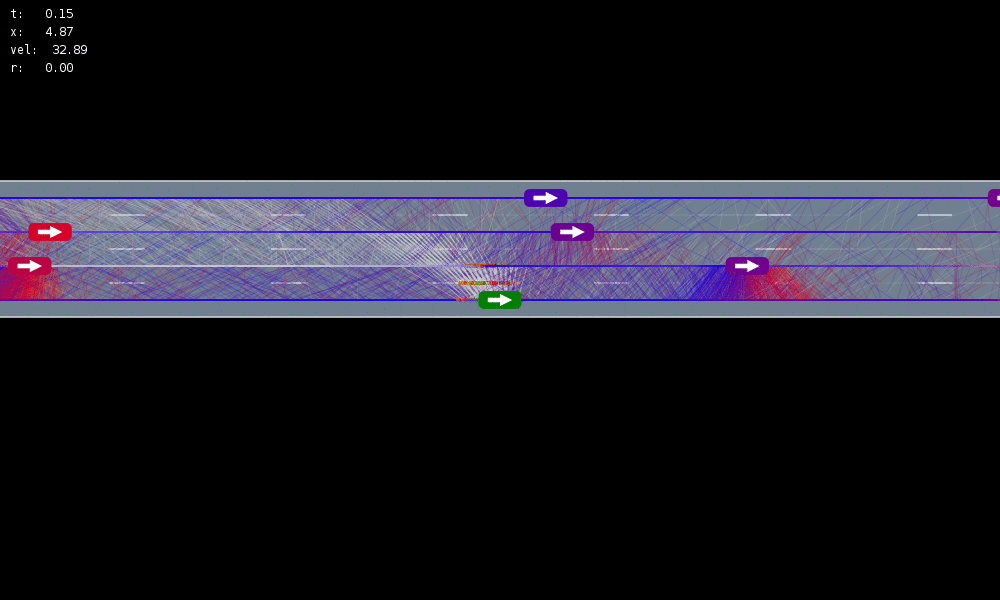
Driving

POMCPOW

POMDPs.jl

Future

POMDPs

Driving

POMCPOW

POMDPs.jl

Future

POMDPs

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

Two Objectives for Autonomy

EFFICIENCY

SAFETY

Minimize resource use

(especially time)

Minimize the risk of harm to oneself and others

Safety often opposes Efficiency

Pareto Optimization

Safety

Better Performance

Model $M_2$, Algorithm $A_2$

Model $M_1$, Algorithm $A_1$

Efficiency

$$\underset{\pi}{\mathop{\text{maximize}}} \, V^\pi = V^\pi_\text{E} + \lambda V^\pi_\text{S}$$

Safety

Weight

Efficiency

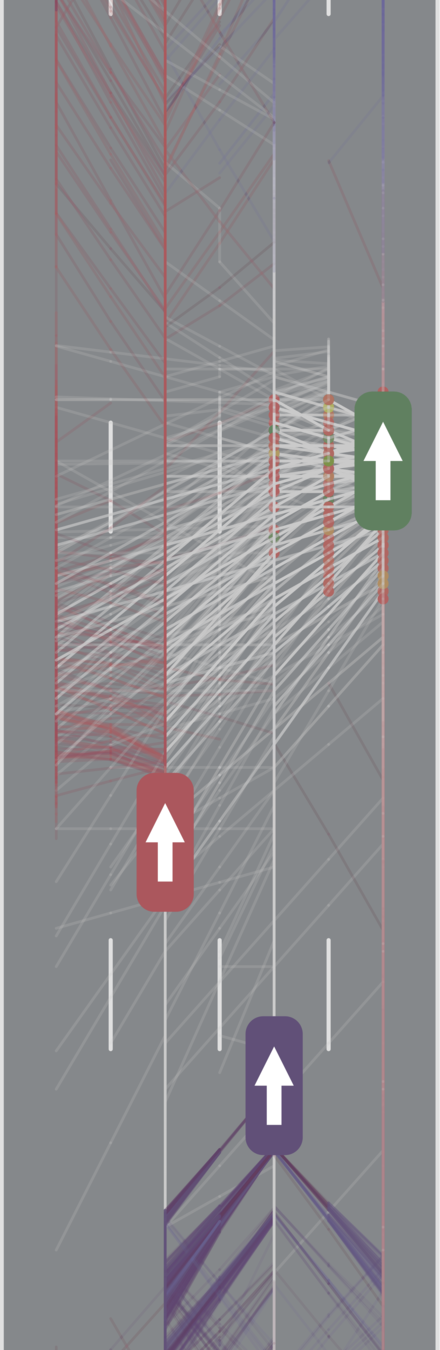
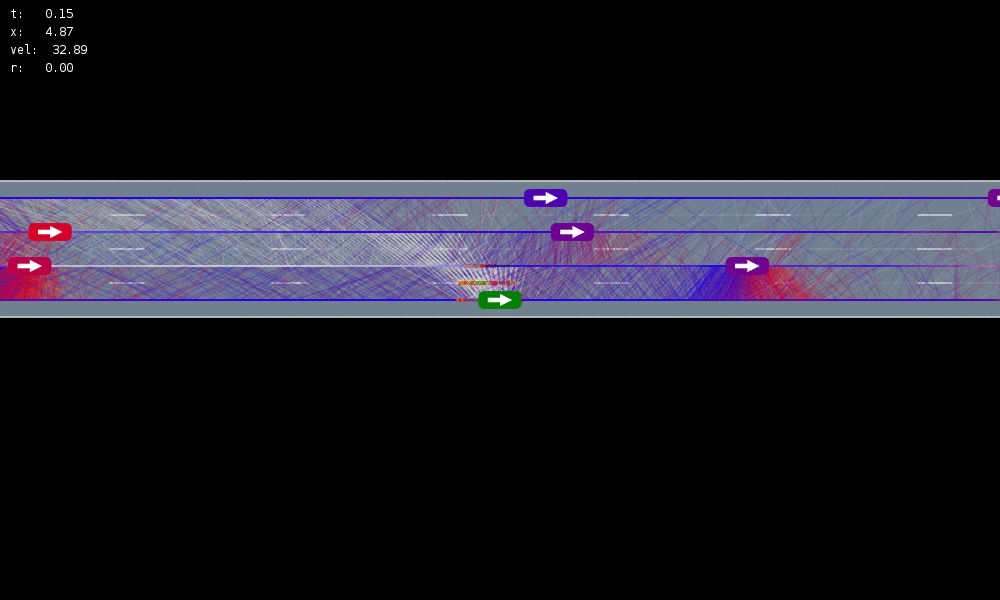
Intelligent Driver Model (IDM)

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]

g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

[Treiber, et al., 2000] [Kesting, et al., 2007] [Kesting, et al., 2009]

Internal States

All drivers normal

No learning (MDP)

Omniscient

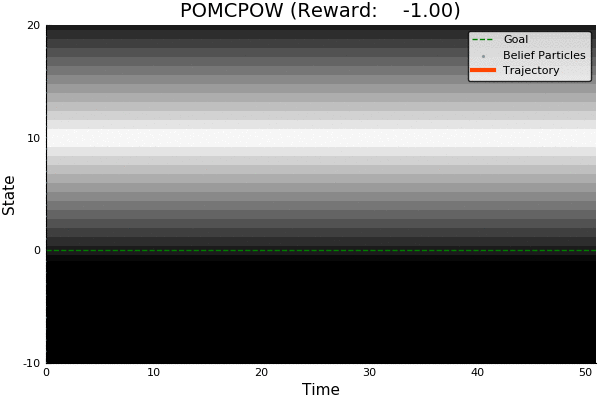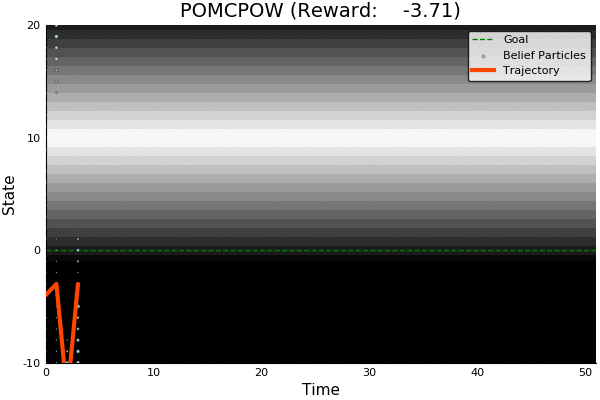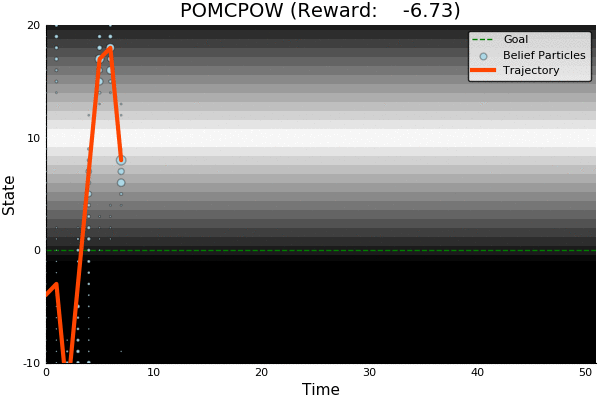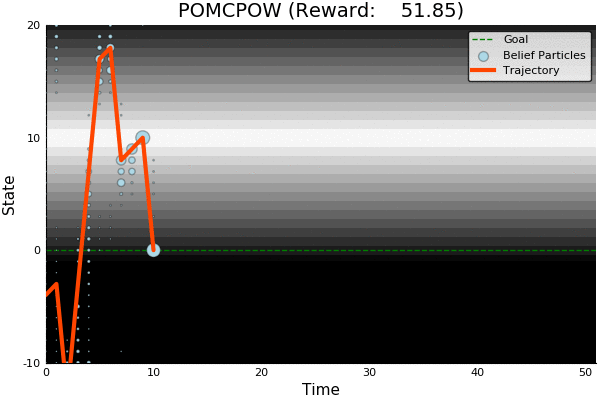
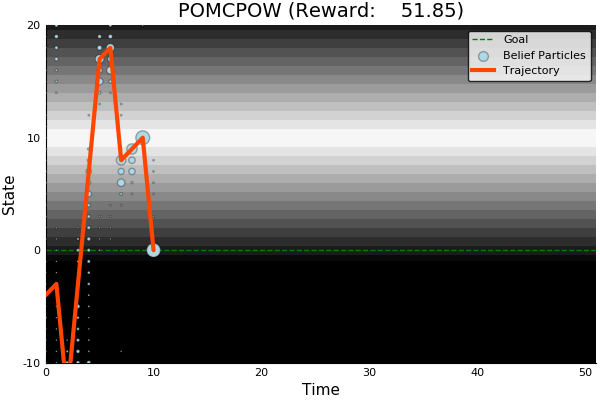
POMCPOW (Ours)

Simulation results

[Sunberg, 2017]

Marginal Distribution: Uniform

$\rho=0$

$\rho=1$

$\rho=0.75$

Internal parameter distributions

Conditional Distribution: Copula

Assume normal

No Learning (MDP)

Omniscient

Mean MPC

QMDP

POMCPOW (Ours)

[Sunberg, 2017]

Driving

POMCPOW

POMDPs.jl

Future

POMDPs

Types of Uncertainty

OUTCOME

MODEL

STATE

Markov Model

$\mathcal{S}$ - State space
$T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}$ - Transition probability distributions

Markov Decision Process (MDP)

$\mathcal{S}$ - State space
$T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Transition probability distribution
$\mathcal{A}$ - Action space
$R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}$ - Reward

Solving MDPs - The Value Function

$$V^*(s) = \underset{a\in\mathcal{A}}{\max} \left\{R(s, a) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=a\Big]\right\}$$

Involves all future time

Involves only $t$ and $t+1$

$$\underset{\pi:\, \mathcal{S}\to\mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, \pi(s_t)) \bigm| s_0 = s \right]$$

$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$

Value = expected sum of future rewards

Online Decision Process Tree Approaches

Time

Estimate $Q(s, a)$ based on children

$$Q(s,a) = R(s, a) + \gamma E\Big[V^* (s_{t+1}) \mid s_t = s, a_t=a\Big]$$

\[V(s) = \max_a Q(s,a)\]

Partially Observable Markov Decision Process (POMDP)

$\mathcal{S}$ - State space
$T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}$ - Transition probability distribution
$\mathcal{A}$ - Action space
$R:\mathcal{S}\times \mathcal{A} \to \mathbb{R}$ - Reward
$\mathcal{O}$ - Observation space
$Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}$ - Observation probability distribution

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

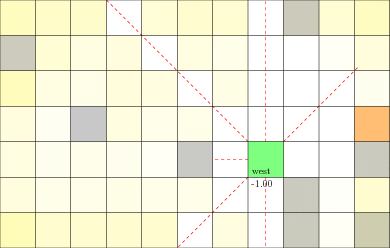
Goal: $a=0$ at $s=0$

Optimal Policy

Localize

$a=0$

POMDP Example: Light-Dark

POMDP Sense-Plan-Act Loop

Environment

Belief Updater

Policy

$b$

$a$

\[b_t(s) = P\left(s_t = s \mid a_1, o_1 \ldots a_{t-1}, o_{t-1}\right)\]

True State

$s = 7$

Observation $o = -0.21$

Environment

Belief Updater

Policy

$a$

$b = \mathcal{N}(\hat{s}, \Sigma)$

True State

$s \in \mathbb{R}^n$

Observation $o \sim \mathcal{N}(C s, V)$

LQG Problem (a simple POMDP)

$s_{t+1} \sim \mathcal{N}(A s_t + B a_t, W)$

$\pi(b) = K \hat{s}$

Kalman Filter

$R(s, a) = - s^T Q s - a^T R a$

Real World POMDPs

1) ACAS

2) Orbital Object Tracking

4) Medical

3) Dual Control

ACAS X

Trusted UAV

Collision Avoidance

[Sunberg, 2016]

[Kochenderfer, 2011]

Real World POMDPs

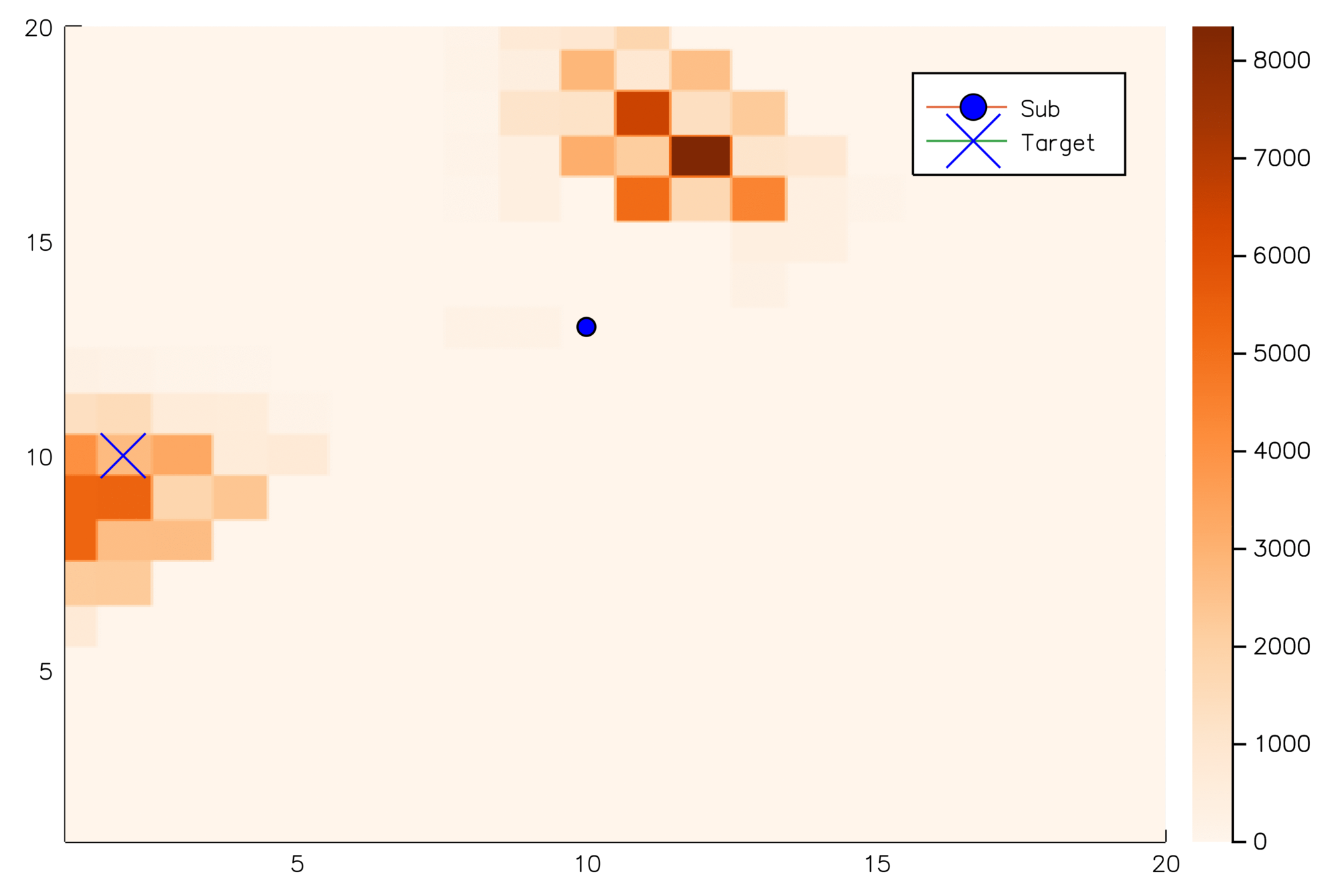
$\mathcal{S}$: Information space for all objects

$\mathcal{A}$: Which objects to measure

$R$: - Entropy

Approximately 20,000 objects >10cm in orbit

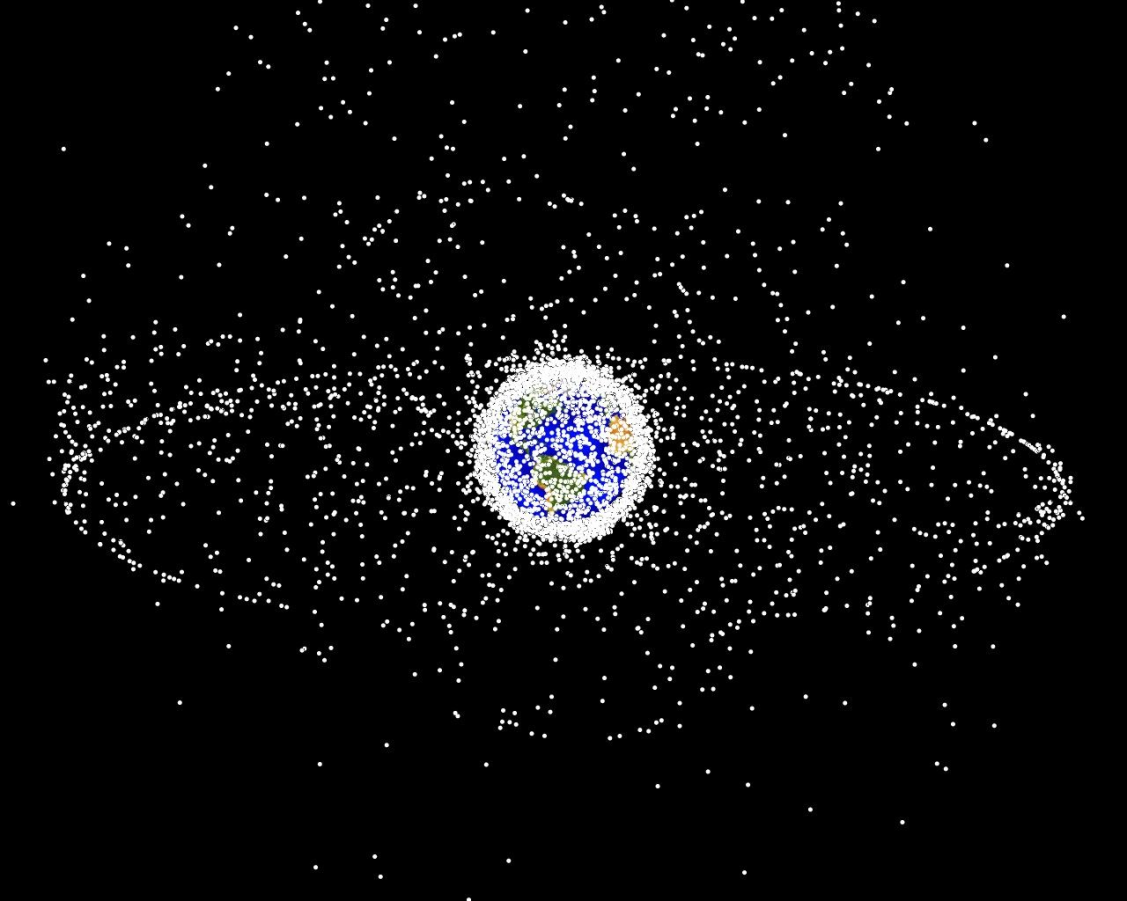
[Sunberg, 2016]

1) ACAS

2) Orbital Object Tracking

4) Medical

3) Dual Control

Real World POMDPs

State $x$ Parameters $\theta$

$s = (x, \theta)$ $o = x + v$

POMDP solution automatically balances exploration and exploitation

[Slade, Sunberg, et al. 2017]

1) ACAS

2) Orbital Object Tracking

4) Medical

3) Dual Control

Real World POMDPs

1) ACAS

2) Orbital Object Tracking

4) Medical

3) Dual Control

[Ayer 2012]

[Sun 2014]

Personalized Cancer Screening

Steerable Needle Guidance

Driving

POMCPOW

POMDPs.jl

Future

POMDPs

POMDP Sense-Plan-Act Loop

Environment

Belief Updater

Policy

$o$

$b$

$a$

A POMDP is an MDP on the Belief Space but belief updates are expensive
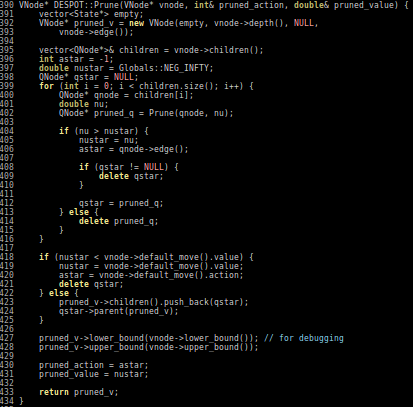
POMCP* uses simulations of histories instead of full belief updates
Each belief is implicitly represented by a collection of unweighted particles

[Ross, 2008] [Silver, 2010]

*(Partially Observable Monte Carlo Planning)

[ ] An infinite number of child nodes must be visited

[ ] Each node must be visited an infinite number of times

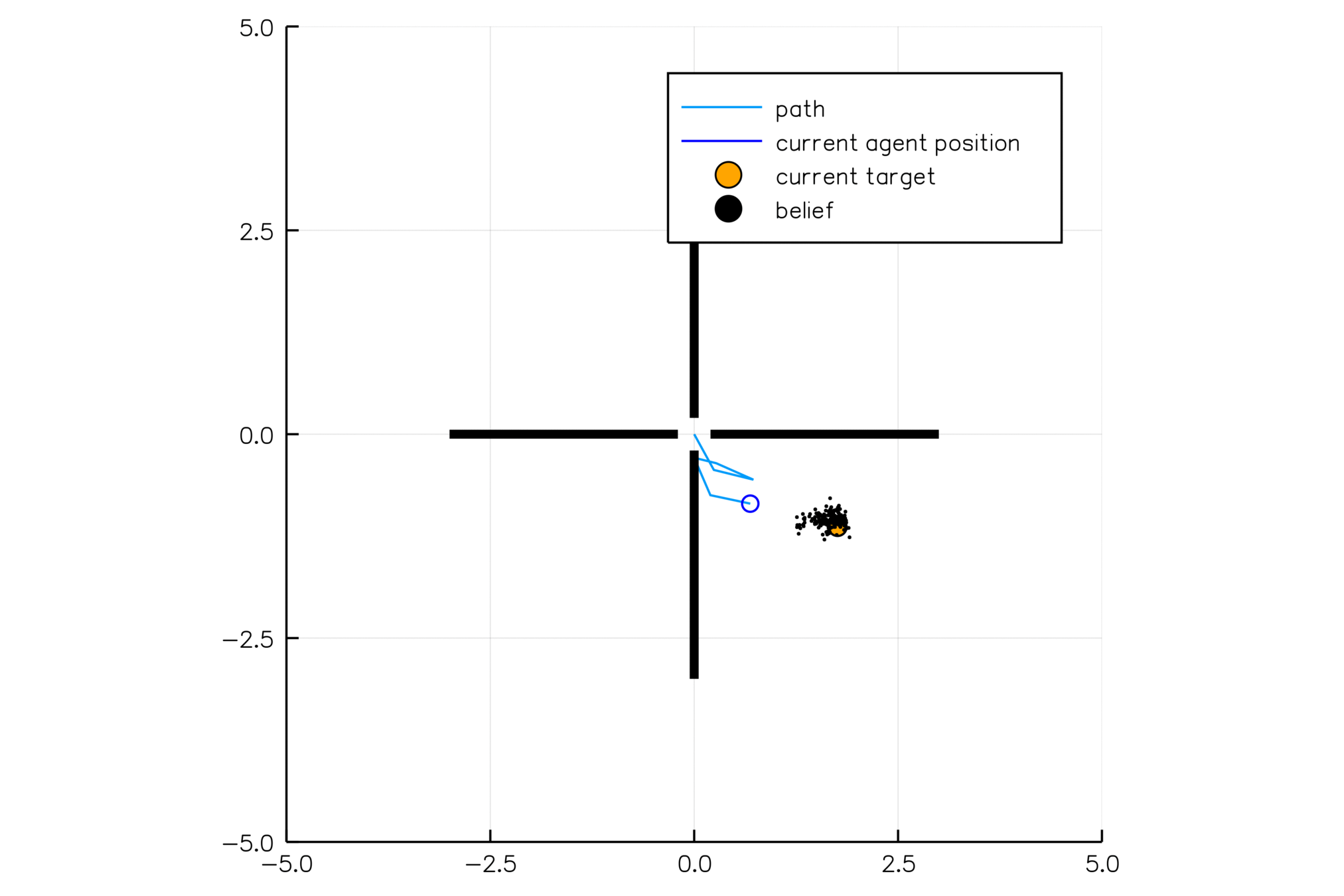
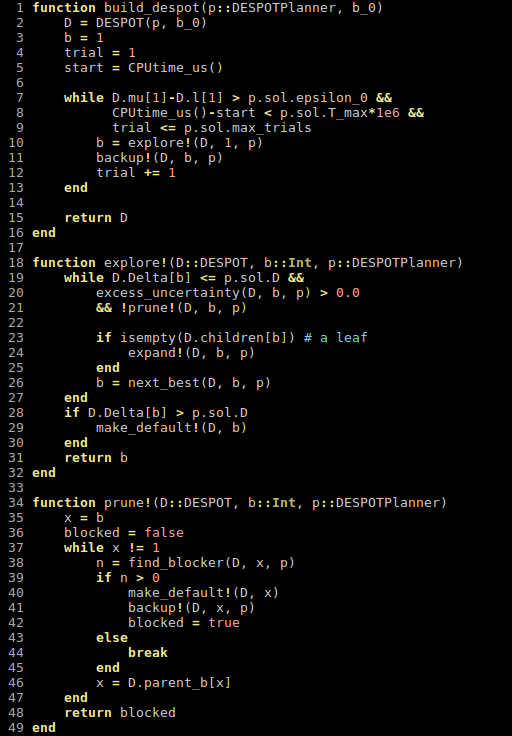
Solving continuous POMDPs - POMCP fails

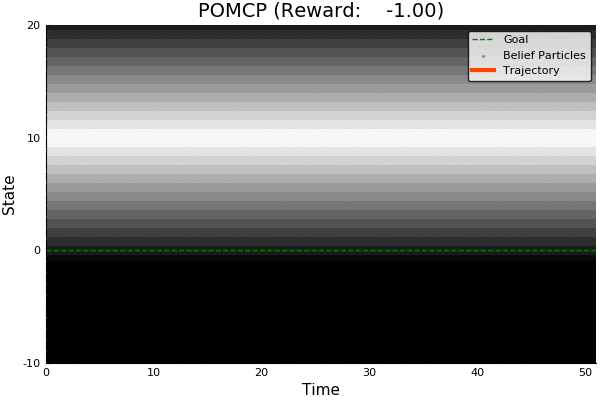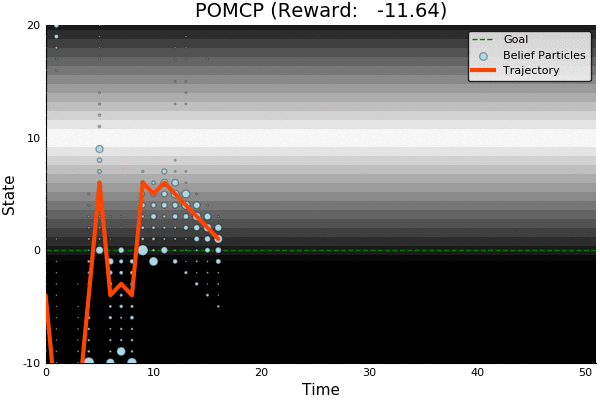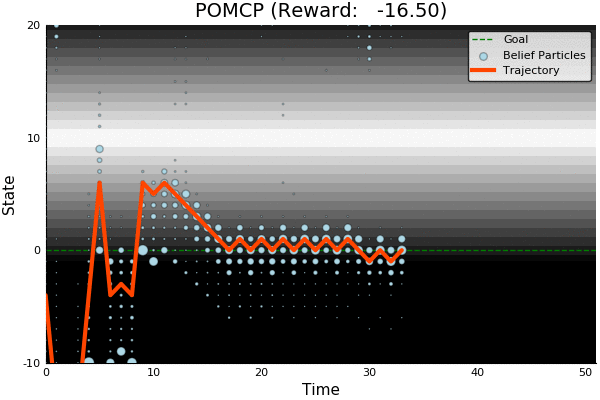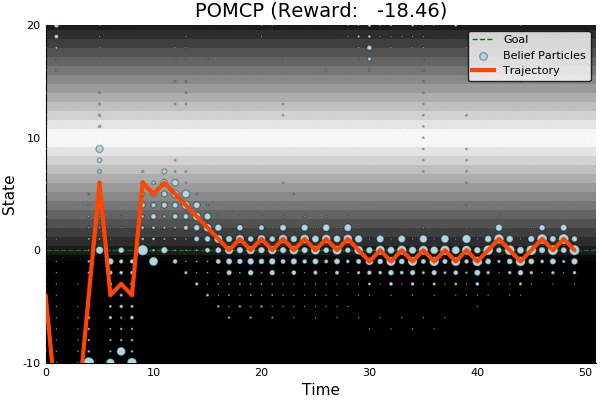
POMCP

✔

Double Progressive Widening (DPW): Gradually grow the tree by limiting the number of children to $k N^\alpha$

Necessary Conditions for Consistency

[Coutoux, 2011]

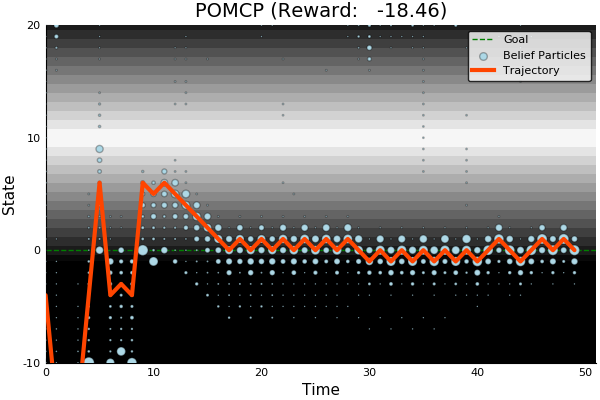
POMCP

POMCP-DPW

[Sunberg, 2018]

POMDP Solution

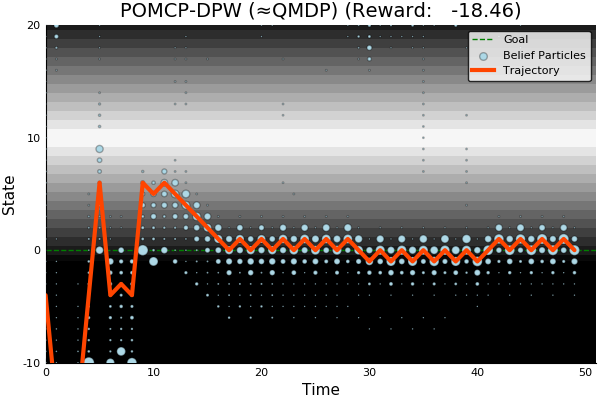
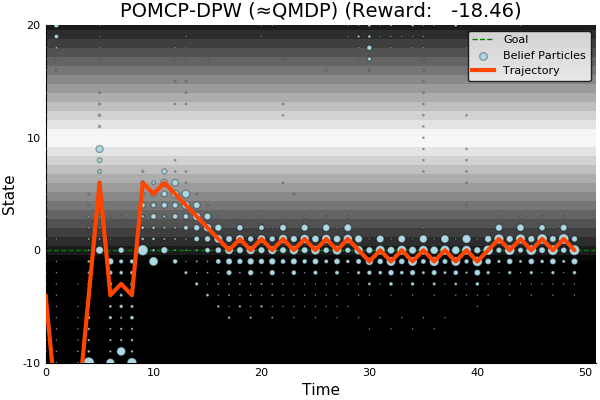
QMDP

\[\underset{\pi: \mathcal{B} \to \mathcal{A}}{\mathop{\text{maximize}}} \, V^\pi(b)\]

\[\underset{a \in \mathcal{A}}{\mathop{\text{maximize}}} \, \underset{s \sim{} b}{E}\Big[Q_{MDP}(s, a)\Big]\]

Same as full observability on the next step

POMCP-DPW converges to QMDP

Proof Outline:

Observation space is continuous with finite density → w.p. 1, no two trajectories have matching observations

(1) → One state particle in each belief, so each belief is merely an alias for that state

(2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state

Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP

[Sunberg, 2018]

POMCP-DPW

[ ] An infinite number of child nodes must be visited

[ ] Each node must be visited an infinite number of times

[ ] An infinite number of particles must be added to each belief node

✔

Necessary Conditions for Consistency

Use $Z$ to insert weighted particles

✔

[Sunberg, 2018]

POMCP

POMCP-DPW

POMCPOW

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Ye, 2017] [Sunberg, 2018]

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

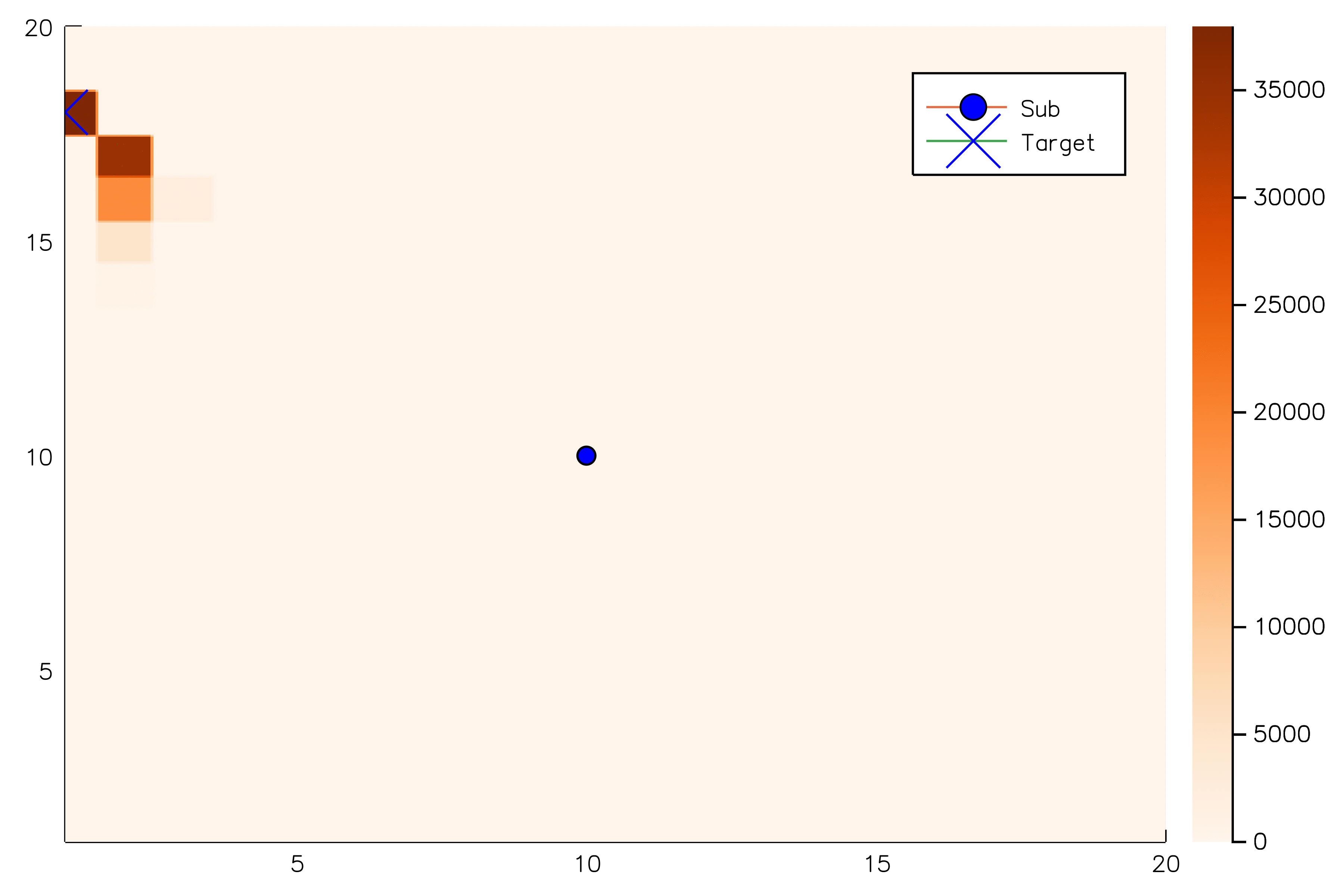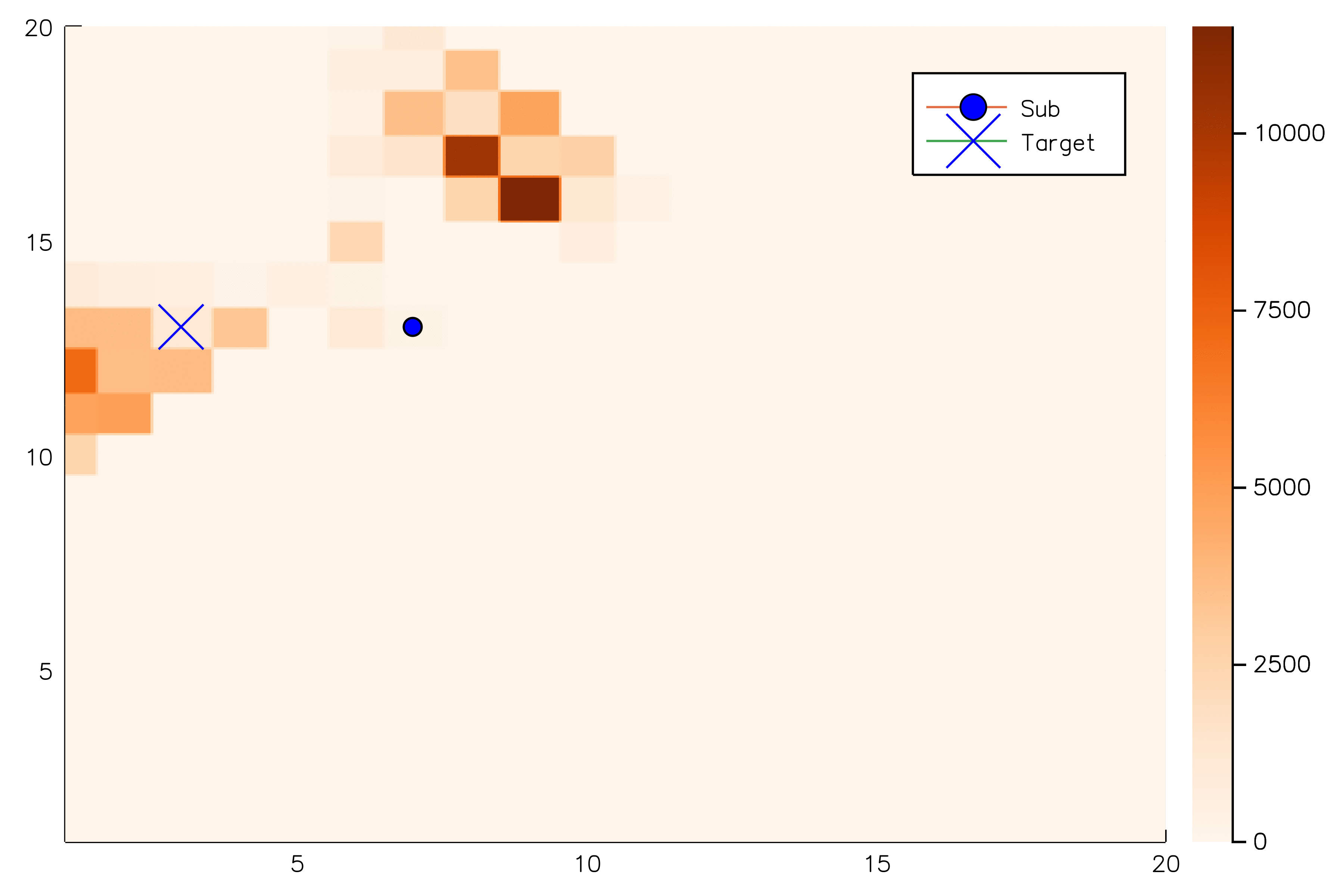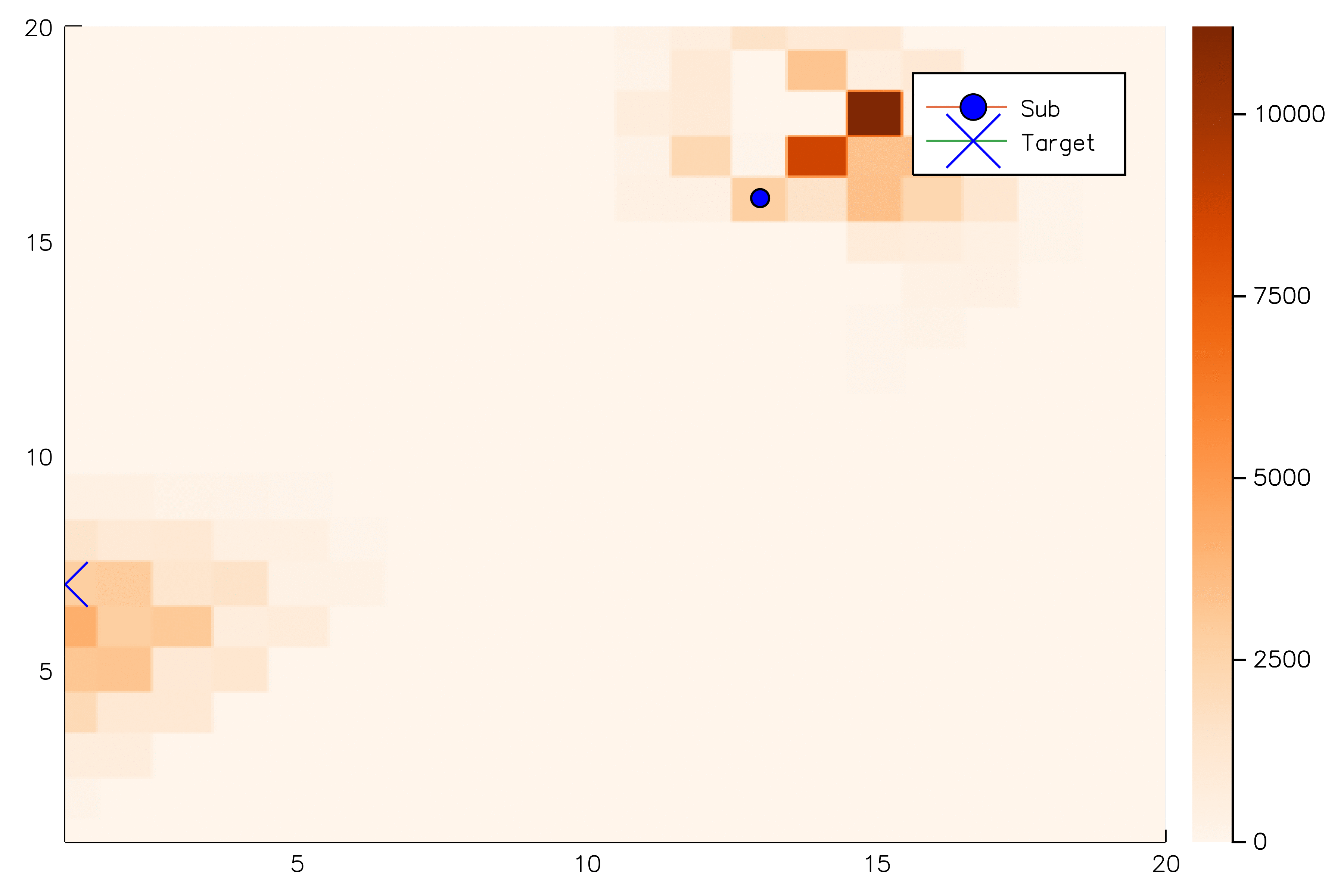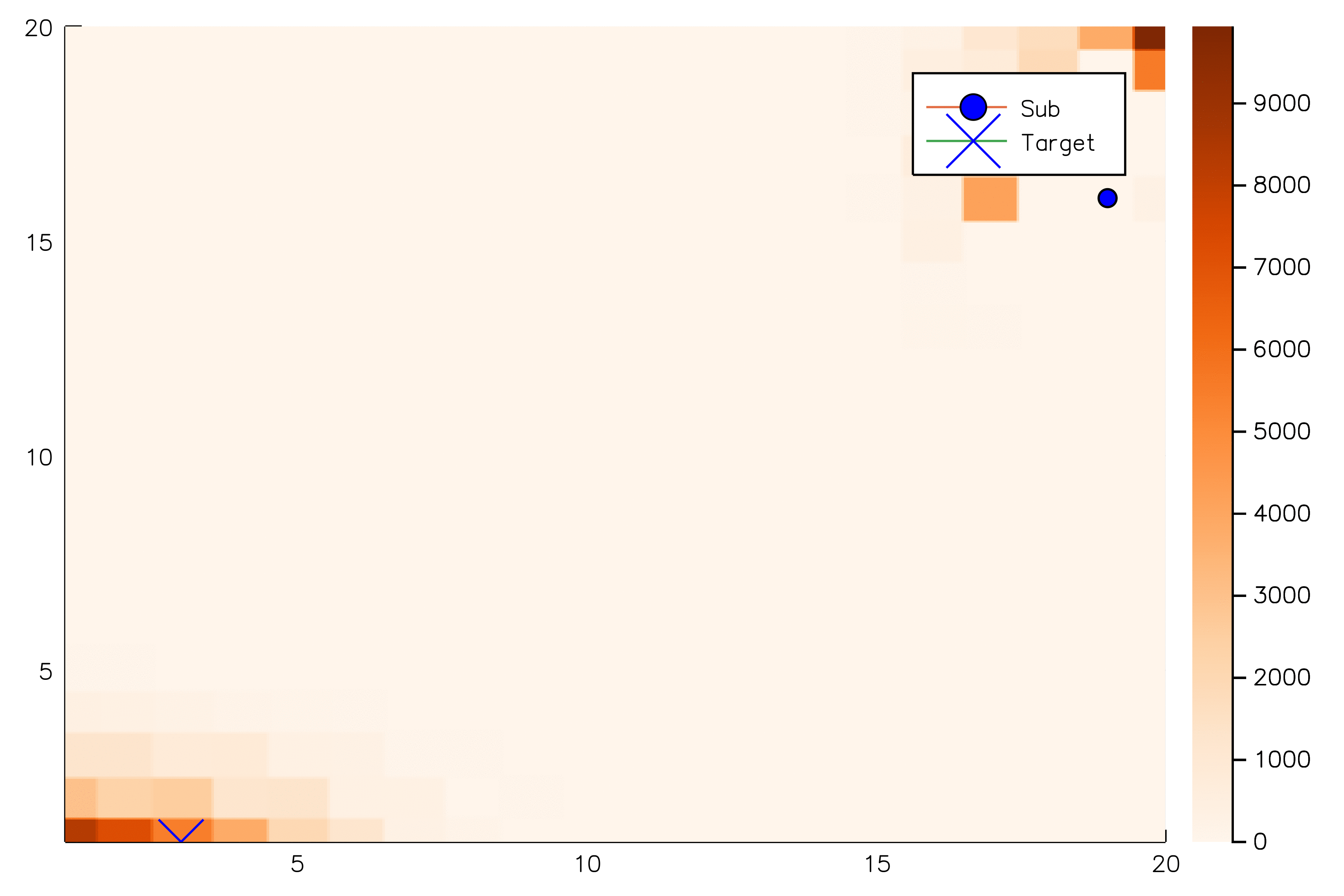
[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

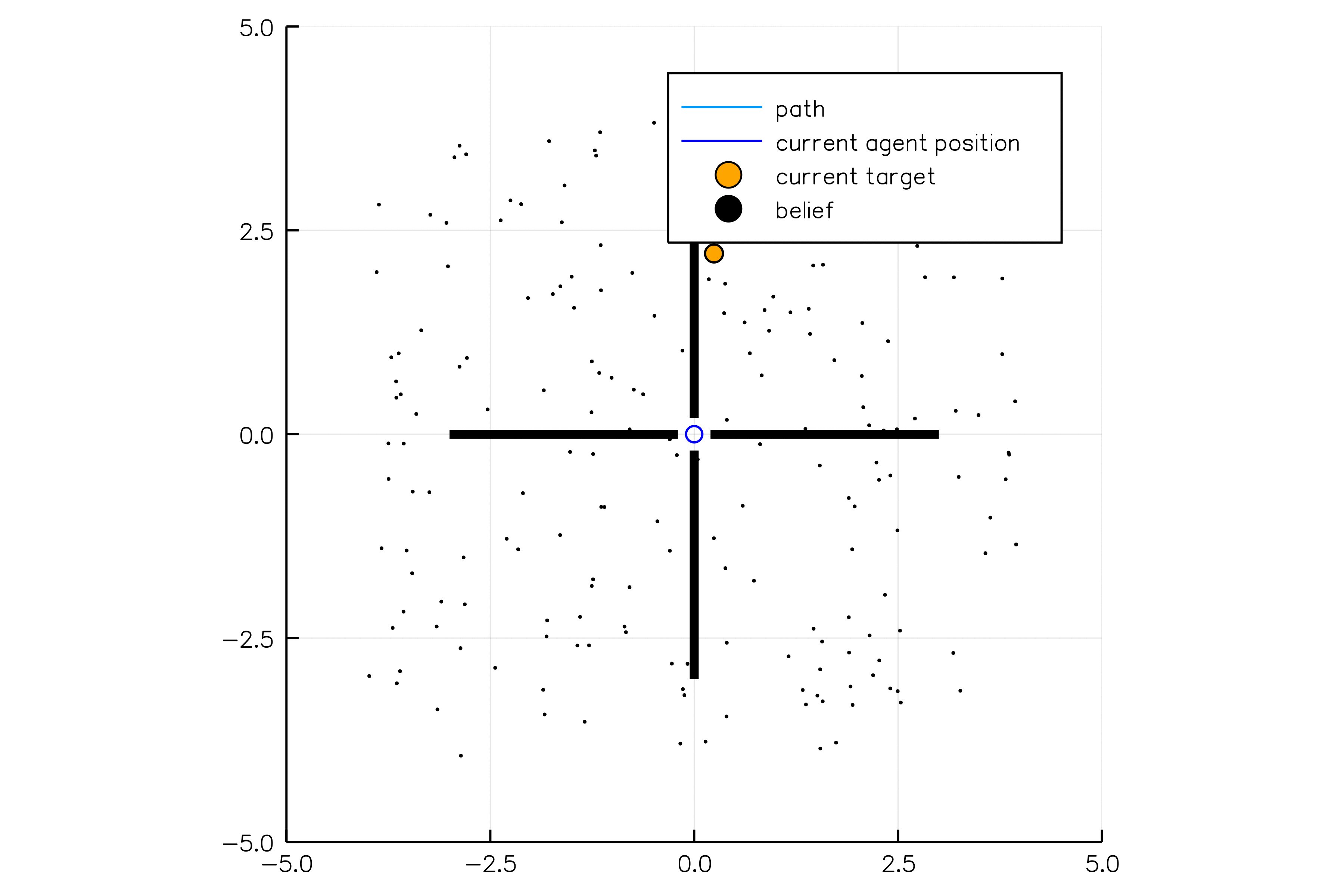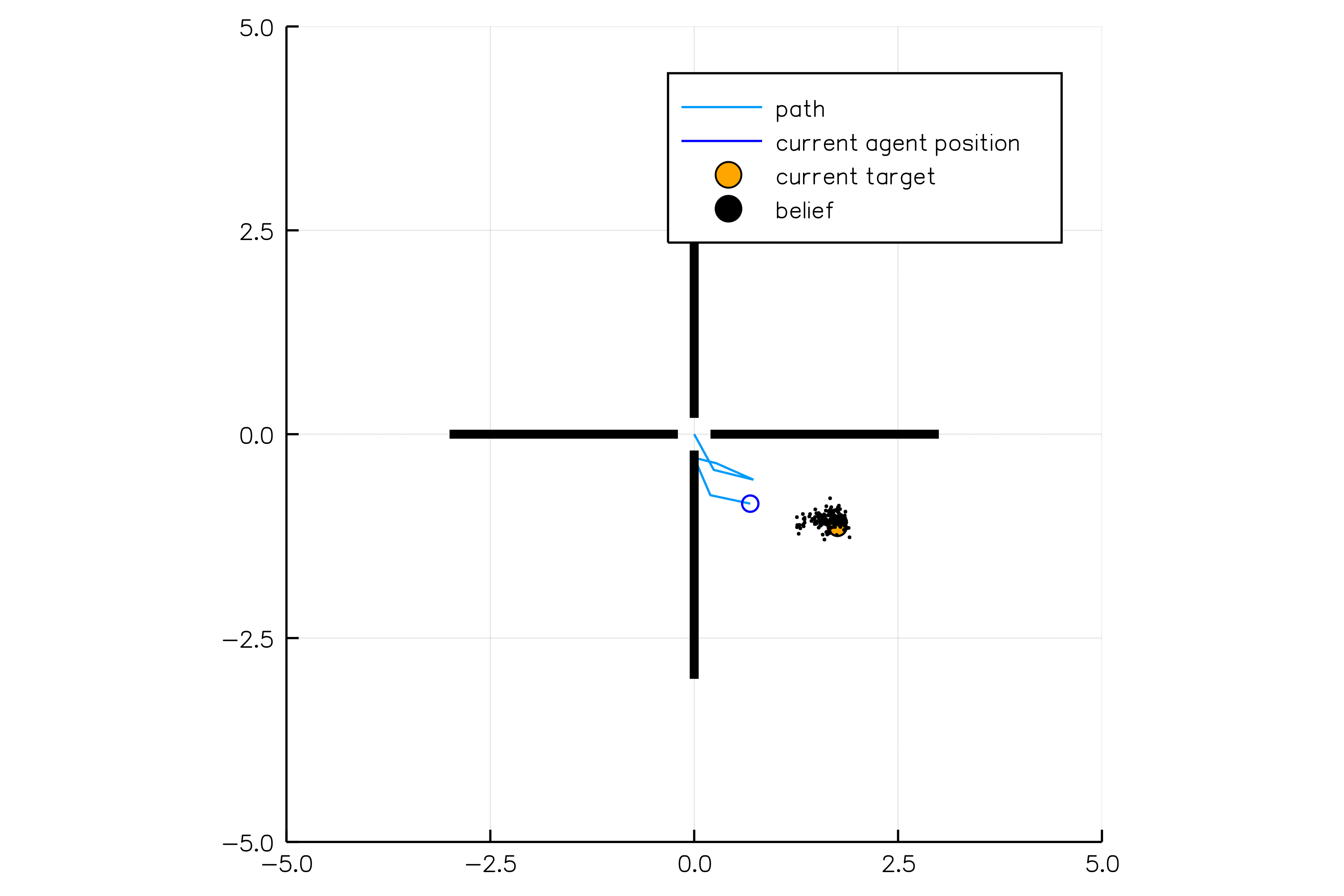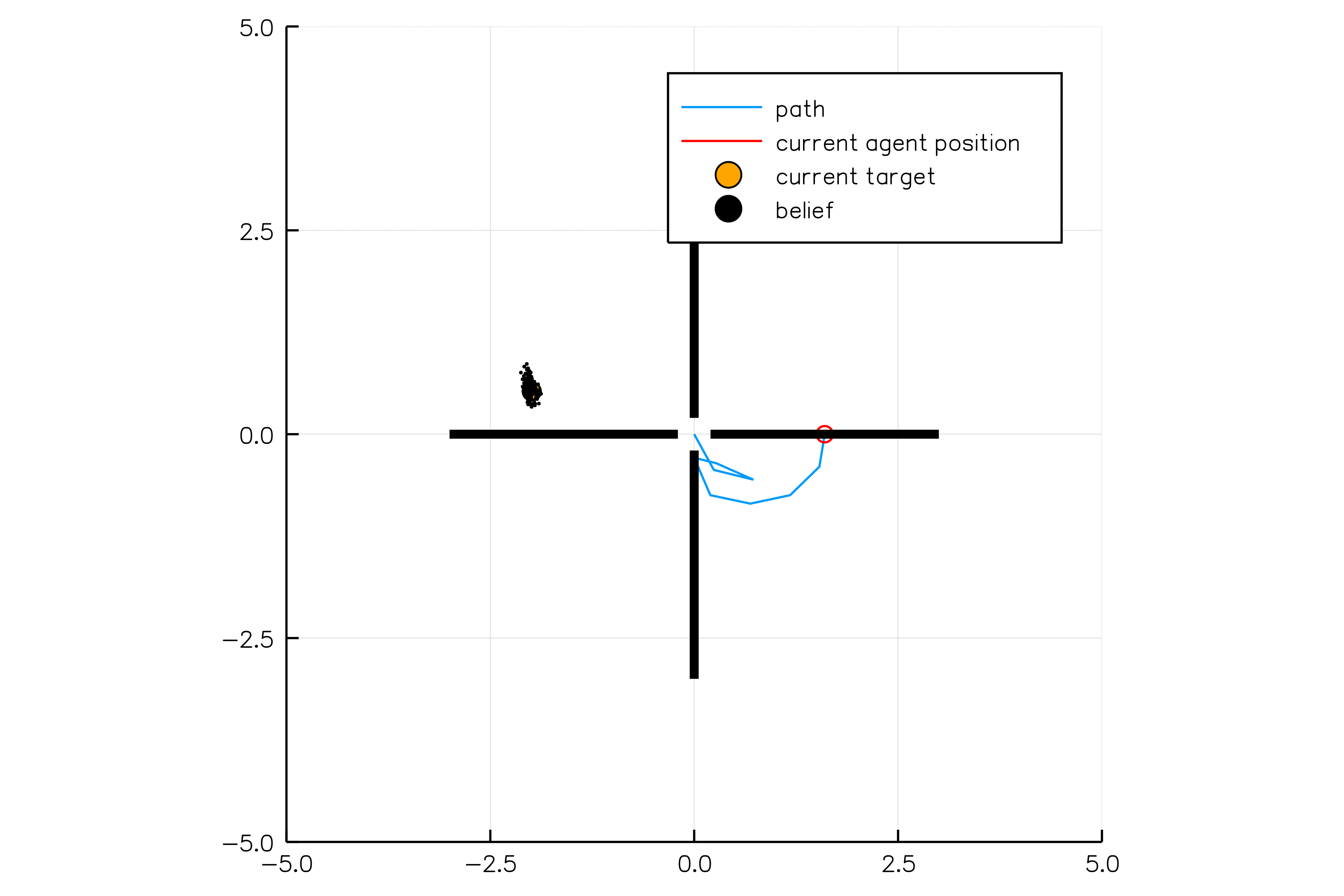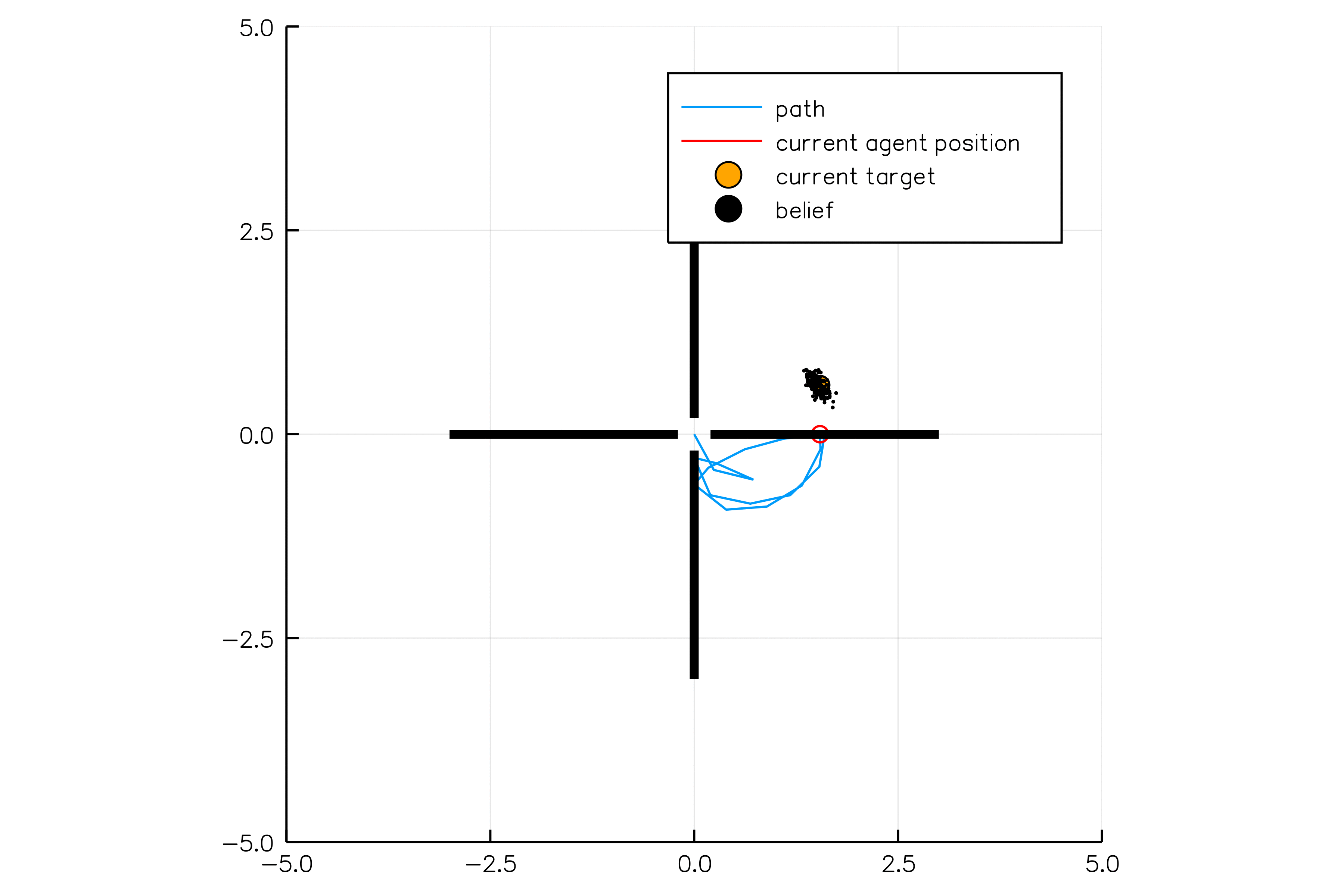
[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Ours

Suboptimal

State of the Art

Discretized

[Sunberg, 2018]

Next Step: Planning on Weighted Scenarios

Driving

POMCPOW

POMDPs.jl

Future

POMDPs

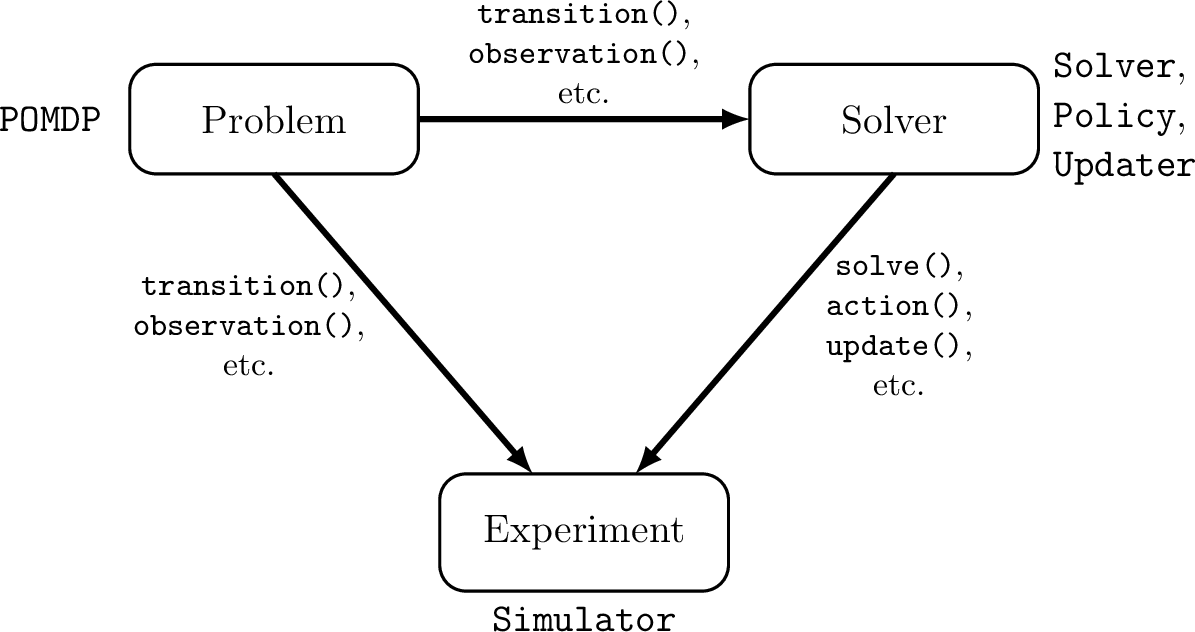
POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

[Egorov, Sunberg, et al., 2017]

Challenges for POMDP Software

POMDPs are computationally difficult.

Julia - Speed

Celeste Project

1.54 Petaflops

Challenges for POMDP Software

POMDPs are computationally difficult.
There is a huge variety of
- Problems
  - Continuous/Discrete
  - Fully/Partially Observable
  - Generative/Explicit
  - Simple/Complex
- Solvers
  - Online/Offline
  - Alpha Vector/Graph/Tree
  - Exact/Approximate
- Domain-specific heuristics

Explicit

Black Box

("Generative" in POMDP lit.)

$s,a$

$s', o, r$

Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

[Egorov, Sunberg, et al., 2017]

using POMDPs, QuickPOMDPs, POMDPSimulators, QMDP

S = [:left, :right]
A = [:left, :right, :listen]
O = [:left, :right]
γ = 0.95

function T(s, a, sp)
    if a == :listen
        return s == sp
    else # a door is opened
        return 0.5 #reset
    end
end

function Z(a, sp, o)
    if a == :listen
        if o == sp
            return 0.85
        else
            return 0.15
        end
    else
        return 0.5
    end
end

function R(s, a)
    if a == :listen  
        return -1.0
    elseif s == a # the tiger was found
        return -100.0
    else # the tiger was escaped
        return 10.0
    end
end

m = DiscreteExplicitPOMDP(S,A,O,T,Z,R,γ)

from julia.QuickPOMDPs import *
from julia.POMDPs import solve, pdf
from julia.QMDP import QMDPSolver
from julia.POMDPSimulators import stepthrough
from julia.POMDPPolicies import alphavectors

S = ['left', 'right']
A = ['left', 'right', 'listen']
O = ['left', 'right']
γ = 0.95

def T(s, a, sp):
    if a == 'listen':
        return s == sp
    else: # a door is opened
        return 0.5 #reset

def Z(a, sp, o):
    if a == 'listen':
        if o == sp:
            return 0.85
        else:
            return 0.15
    else:
        return 0.5

def R(s, a):
    if a == 'listen':
        return -1.0
    elif s == a: # the tiger was found
        return -100.0
    else: # the tiger was escaped
        return 10.0

m = DiscreteExplicitPOMDP(S,A,O,T,Z,R,γ)