Topiary and the Art of Origami
Exploring decision trees with recursion schemes
@_zainabali_
Zainab Ali
Predicting survival on the Titanic
- Shipwreck
- Over 60% died
- Not enough lifeboats
- Stochastic
- Can we predict survival?
The Journey
- basic predictions
- use decision trees
- matryoshka
- anamorphisms
- catamorphisms
- hylomorphisms
- cost complexity pruning
Input Example
Output Label
case class Example(
gender: Gender,
age: Age,
ticketClass: TicketClass,
familySize: FamilySize
)
sealed trait Label
case object Survived
extends Label
case object Died
extends Label
1000 examples
binary classification
Hypothesis
def predict(example: Example): Label
- train on a subset of examples
- test on the rest
Hypothesis: Everyone Dies
def predict(example: Example): Label = Died
Risk
def risk(predictions: Map[Int, Label],
actual: Map[Int, Label]): Double = {
predictions.map {
case (id, prediction) =>
if (prediction != actual(id)) 1.0 else 0.0
} / predictions.size
}
Fraction of incorrect predictions
Risk: Everyone Dies
39.5%
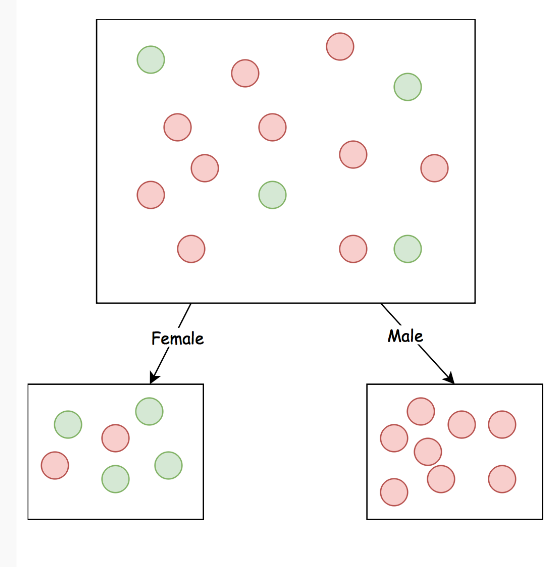
Females Survive
def predict(example: Example): Label =
example.gender match {
case Female => Survived
case Male => Died
}
Risk: Females Survive
24% (-15.5)
Entropy
Matryoshka
Recursion schemes

Decision tree
sealed trait Tree
case class Leaf(label: Label) extends Tree
case class Node(feature: Feature,
children: Map[Value, Tree]) extends Tree
sealed trait TreeF[A]
case class Leaf[A](label: Label) extends TreeF[A]
case class Node[A](feature: Feature,
children: Map[Value, A]) extends TreeF[A]
Fix
case class Fix[F[_]](unFix: F[Fix[F]])
val tree: Fix[TreeF] = Fix(Node(gender, Map(
"male" -> Fix(Leaf[Fix[TreeF]](Died)),
"female" -> Fix(Leaf[Fix[TreeF]](Survived))
)))
type Tree = Fix[TreeF]

It needs a Functor
implicit val treeFunctor: Functor[TreeF] =
new Functor[TreeF] {
def map[A, B](fa: TreeF[A])(f: A => B): TreeF[B] =
fa match {
case Leaf(l) => Leaf(l)
case Node(feature, children) =>
Node(feature, children.mapValues(f))
}
}
Anamorphism
type Coalgebra[F[_], A] = A => F[A]
def ana[F[_]: Functor, A](a: A)(
coalgebra: Coalgebra[F, A]): Fix[F]
Generalized unfold

Building the tree
type Input = (List[Example], Set[Feature])
val build: Coalgebra[TreeF, Input] = {
case (examples, features) =>
if(features.nonEmpty) {
val (feature, maxGain) = maxGain(examples, features)
val nextFeatures = features - feature
val nextExamples = groupByValue(examples, feature)
Node(feature, nextExamples.mapValues(xs =>
(xs, nextFeatures)))
} else {
Leaf(mostCommonLabel(examples))
}
}
val tree: Tree = (examples, features).ana(build)
Anamorphism
val tree: Tree = (examples, features).ana(build)
Prediction: exploring a path
def explore(example: Example):
Coalgebra[Label Either ?, Tree] =
_.unFix match {
case Leaf(label) => Left(label)
case Node(feature, children) =>
Right(children(value(feature, example)))
}Anamorphism with Either
Prediction: exploring a path
val lizWalton: Example = Example(Adult, Female, ...)
val path: Fix[Label Either ?] = tree.ana(explore(lizWalton))
//path = Fix(Right(Fix(Right(...(Fix(Left(Label.Survived))))
Catamorphism
type Algebra[F[_], A] = F[A] => A
def cata[F[_]: Functor, A](fix: Fix[F])(
algebra: Algebra[F, A]): A
Generalized fold

Prediction: collapsing the path
val collapse: Algebra[Label Either ?, Label] = _.merge
val prediction = path.cata(collapse)
//prediction = SurvivedHylomorphism
def hylo[F[_]: Functor, A, B](a: A)(
algebra: Algebra[F[_], B],
coalgebra: Coalgebra[F[_], A]): B
Generalized refold

Hylomorphism
def predict(tree: Tree)(example: Example): Label =
tree.hylo(collapse, explore(example))
Risk: Decision Tree (training)
15.1%
Risk: Decision Tree
(test)
24.0% (-0.0)
Overfitting
topiary time!
Cost Complexity Pruning
- Annotate T0 with label counts
- Annotate with cost
- Find minimum cost
- Snip off node with minimum cost to create T1
- Repeat 3 and 4 to get T2 ...
- Create a series of subtrees T0, T1, T2 ... Leaf
Cost
- current risk
- resubstitution risk of replacing node with leaf
- number of leaves removed
g(n) = (R(n) - R(T)) / (L - 1)
g(n)=(R(n)−R(T))/(L−1)
Tagging
case class AttrF[A, B](a: A, tree: TreeF[B])
implicit def attrFunctor[A]: Functor[AttrF[A, ?]] = ...
Tag with counts
type Counts = Map[Label, Int]
def buildCounts: Coalgebra[AttrF[Counts, ?], Input] = {
case (examples, features) =>
val counts = labelCounts(examples)
val tree = build((examples, features))
AttrF(counts, tree)
}
val tree = (examples, features).ana(buildCounts)
Tag with cost
case class CostInfo(
leafCount: Int,
risk: Int,
counts: Counts
)
val costInfo: Algebra[AttrF[Counts, ?], Attr[CostInfo]] = {
case AttrF(counts, t: Leaf(_)) =>
Fix(AttrF(leafCostInfo(counts, t), t))
case AttrF(_, t @ Node(_, children)) =>
Fix(AttrF(nodeCostInfo(children), t))
}
tree.cata(costInfo)
Another hylo!
val tree = (examples, features)
.ana(buildCounts)
.cata(costInfo)
val tree = (examples, features).hylo(buildCounts, costInfo)
Find min cost
val minCost: Algebra[AttrF[CostInfo, ?], Double] = {
case AttrF(_, Leaf(_)) => Double.PositiveInfinity
case AttrF(info, Node(_, children)) =>
(info.cost :: children.values).min
}
tree.cata(minCost)
Prune
def prune(minCost: Double):
Algebra[AttrF[CostInfo, ?], Attr[CostInfo]] = {
case AttrF(c, Leaf(l)) =>
Fix(AttrF(c, Leaf(l)))
case AttrF(info, n @ Node(_, children)) =>
if(info.cost == minCost) {
val leaf = makeLeaf(info)
Fix(AttrF(leafCostInfo(info.counts, leaf), leaf))
} else {
Fix(AttrF(nodeCostInfo(children), n))
}
}
tree.cata(prune(minCost))
Cost Complexity Pruning
val tree = (examples, features)
.hylo(buildCounts, costInfo)
val cost1 = tree.cata(minCost)
val subTree1 = tree.cata(prune(cost1))
val cost2 = subTree1.cata(minCost)
val subTree2 = subTree1.cata(prune(cost2))
...
Which subtree?
- Split data into training and validation
- Build trees on training data
- Validate on validation data
- Pick the subtree with the lowest risk
Risk: Pruned Tree
22.4% (-1.6)
Yay!
We've come a long way
- Anamorphisms
- Catamorphisms
- Hylomorphisms
Where to next?
- Dimensionality reduction
- Cross validation
- Ensemble methods
You may be interested in
- The code https://github.com/zainab-ali/titanic
- Matryoshka https://github.com/slamdata/matryoshka

We're hiring!