\mathit{\Pi}(s)
=
\displaystyle
\lim_{K \to \infty}
\frac {1 \cdot 2 \cdot 3 \cdots K}{(s+1)(s+2)(s+3) \cdots (s+K)}
(K+1)^s
Π(s)=K→∞lim(s+1)(s+2)(s+3)⋯(s+K)1⋅2⋅3⋯K(K+1)s
と定義し,
\mathit{\Pi}(s)
Π(s)
を
\displaystyle \frac{x}{e^x-1} = \sum_{k=0}^{\infty}\frac{B_k}{k!}x^k
ex−1x=k=0∑∞k!Bkxk
に対して,
k>1
k>1
B_k
Bk
を定め,
\overline{B}_k(x)
=
B_k(x-[x])
Bk(x)=Bk(x−[x])
として
\overline{B}_k(x)
Bk(x)
と定義する.
k
k
次のBernoulli多項式を, 次数
k
k
の多項式で
\displaystyle \int_x^{x+1}
B_k(t)dt
=
x^k
∫xx+1Bk(t)dt=xk
という性質を満たす唯一のものとして定義する. そして,
を
としたとき,
\log\mathit{\Pi}(s)
=
(s+\frac{1}{2})
\log(s+1)
+A
-1
-
\displaystyle \int_1^{\infty}
\frac{\overline{B}_1(x)}{s+x}dx - s
logΠ(s)=(s+21)log(s+1)+A−1−∫1∞s+xB1(x)dx−s
が成り立つことを確認せよ.
A
=
1
+
\displaystyle \int_1^{\infty}
\frac{\overline{B}_k(x)}{x}dx
A=1+∫1∞xBk(x)dx
ここで, 定数
A
A
を
d:
\mathbb{N}
\to
\mathbb{N}
d:N→N
を, 自然数の10進表記における桁を返す写像とする.
K=d(y).
K=d(y).
次の方程式は自然数解
(x, y, K)
(x,y,K)
(1).
(1).
を無数にもつことを示せ.
\displaystyle
x^2
+
y^2
=
x
\cdot
10^K
+
y
~,
x2+y2=x⋅10K+y ,
(2).
(2).
p
p
を素数とする.
\displaystyle
p=
x^2
+
y^2
=
x
\cdot
10^K
+
y
~,
p=x2+y2=x⋅10K+y ,
K=d(y)
K=d(y)
となるような
p
p
は
101
101
と
5882353
5882353
のみであることを示せ.
\displaystyle
\psi
(x)
=
\sum_{k=1}^{\infty}
\exp
(-k^2
\pi
x)
ψ(x)=k=1∑∞exp(−k2πx)
\displaystyle
\zeta(s)
=
\sum_{k=1}^{\infty}
\frac{1}{k^s}
ζ(s)=k=1∑∞ks1
\displaystyle
\mathit{\Pi}(s)
=
\displaystyle
\lim_{K \to \infty}
\frac {1 \cdot 2 \cdot 3 \cdots K}{(s+1)(s+2)(s+3) \cdots (s+K)}
(K+1)^s
Π(s)=K→∞lim(s+1)(s+2)(s+3)⋯(s+K)1⋅2⋅3⋯K(K+1)s
\displaystyle
\mathit{\xi}(s)
=
\mathit{\Pi}(\frac{s}{2})
(s-1)
\pi^{-\frac{s}{2}}
\zeta(s)
ξ(s)=Π(2s)(s−1)π−2sζ(s)
と関数
\displaystyle
\zeta(s)
ζ(s)
\displaystyle
\psi(s)
ψ(s)
,
,
\displaystyle
\mathit{\xi}(s)
ξ(s)
,
\displaystyle
\mathit{\Pi}(s)
Π(s)
を定義する.
\displaystyle
=
\frac{1}{2}
+
\psi(1)-
\psi'(1)
(-2-2)
+
\int_1^\infty
\frac{d}{dx}
(x^\frac{3}{2}
\psi'(x))
(-2x^\frac{(s-1)}{2}
-
2x^{-\frac{s}{2}})
dx
=21+ψ(1)−ψ′(1)(−2−2)+∫1∞dxd(x23ψ′(x))(−2x2(s−1)−2x−2s)dx
\displaystyle
\mathit{\xi}(s)
ξ(s)
が成り立つことを確認せよ.
\displaystyle
\int_{+\infty}^{+\infty}
\frac {(-x)^s}{e^x-1}
\frac{dx}{x}
=
(e^{i\pi s}-e^{-i\pi s})
\int_{0}^{\infty}
\frac{x^{s-1}dx}{e^x-1}
∫+∞+∞ex−1(−x)sxdx=(eiπs−e−iπs)∫0∞ex−1xs−1dx
の定義は
\displaystyle
(-x)^s
(−x)s
\displaystyle
(-x)^s
=
\exp(s \log(-x))
(−x)s=exp(slog(−x))
\displaystyle
\log (-x)
log(−x)
\displaystyle
\log z
logz
ここで
であり,
の通常の定義である.
の定義は
このとき,
が成り立つことを確認せよ. ただし
\displaystyle
\Re ~ s>1
ℜ s>1
.
\displaystyle
\int_{0}^{\infty i^{\frac{1}{2}}}
\biggl(
\frac{-1}{1-e^{-2\pi i \nu}}
\biggl)
\nu ^{-s}
d\nu
∫0∞i21(1−e−2πiν−1)ν−sdν
\displaystyle
\zeta(s)
=
\sum_{k=1}^{\infty}
\frac{1}{k^s}
ζ(s)=k=1∑∞ks1
\displaystyle
\mathit{\Pi}(s)
=
\displaystyle
\lim_{K \to \infty}
\frac {1 \cdot 2 \cdot 3 \cdots K}{(s+1)(s+2)(s+3) \cdots (s+K)}
(K+1)^s
Π(s)=K→∞lim(s+1)(s+2)(s+3)⋯(s+K)1⋅2⋅3⋯K(K+1)s
\displaystyle
=
\zeta (1-s)
i
e^{- \frac{i\pi s}{2}}
(2\pi)^{s-1}
1^{s-1}
\mathit{\Pi}(-s)
=ζ(1−s)ie−2iπs(2π)s−11s−1Π(−s)
と関数
\displaystyle
\zeta(s)
ζ(s)
,
\displaystyle
\mathit{\Pi}(s)
Π(s)
をそれぞれ定義する. このとき,
が成り立つことを示せ.
\displaystyle
\zeta
ζ
\displaystyle
\mathrm{Mellin}
Mellin
\displaystyle
\longleftrightarrow
⟷
\displaystyle
\Theta
Θ
\displaystyle
\smile
⌣
\displaystyle
\longleftarrow
⟵
\displaystyle
\mathrm{IUTeich}
IUTeich
\displaystyle
\mathbb{Z} \longleftrightarrow \mathbb{F}_{q} [\tau]
Z⟷Fq[τ]
\displaystyle
\longrightarrow
⟶
\displaystyle
\mathbb{Z} ~ \otimes ~ \mathbb{Z}
Z ⊗ Z
\displaystyle
\rightarrow
→
\displaystyle
\mathbb{Z} ~~~ \Delta
Z Δ
\displaystyle
\mathrm{IU ~ Fourier}
IU Fourier
\displaystyle
\mathbb{F}_{1}
F1
``
‘‘
"
"
\displaystyle
``\Delta . \Delta + \varepsilon \Gamma_{\mathrm{Fr}} "
‘‘Δ.Δ+εΓFr"
\displaystyle
= \Delta . \Delta + \varepsilon \Delta . \Gamma_{\mathrm{Fr}}
=Δ.Δ+εΔ.ΓFr
Main term
Error term
\displaystyle
\leadsto
⇝
??
\displaystyle
\mathrm{Mellin}
Mellin
\displaystyle
1 + \varepsilon \Delta . \Gamma_{\mathrm{Fr}} + \frac{1}{2} (\varepsilon \mathrm{Fr})^{2} + \cdots
1+εΔ.ΓFr+21(εFr)2+⋯
\displaystyle
\hookrightarrow
↪
\displaystyle
\mathrm{Fr}
Fr
\displaystyle
\Delta . \Gamma_{\mathrm{Fr}}
Δ.ΓFr
Riemann Hypothesis
\displaystyle
\longleftarrow
⟵
\displaystyle
\pi (x) = \sum_{p \leqq x} 1
π(x)=p≦x∑1
\displaystyle
\vartheta (x) = \sum_{p \leqq x} \log p
ϑ(x)=p≦x∑logp
\displaystyle
\psi (x) = \sum_{p^{m} \leqq x} \log p
ψ(x)=pm≦x∑logp
\displaystyle
\psi_{1} (x) = \int_{1}^{x} \psi (t) dt
ψ1(x)=∫1xψ(t)dt
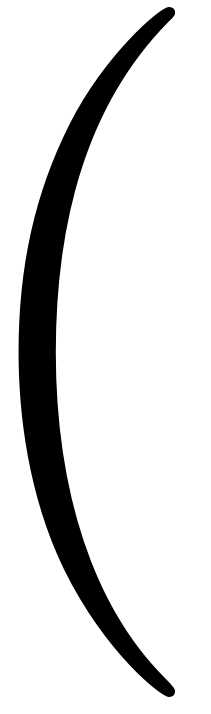
\displaystyle
\psi_{1} (x) \sim \frac{x^{2}}{2}
~~~
(x \to \infty)
ψ1(x)∼2x2 (x→∞)
\displaystyle
\psi (x) \sim x
~~~
(x \to \infty)
ψ(x)∼x (x→∞)
\displaystyle
\vartheta (x) \sim x
~~~
(x \to \infty)
ϑ(x)∼x (x→∞)
\displaystyle
\pi (x) \sim \frac{x}{\log x}
~~~
(x \to \infty)
π(x)∼logxx (x→∞)
\displaystyle
\Uparrow
⇑
\displaystyle
\Uparrow
⇑
\displaystyle
\Uparrow
⇑
←``重さ
\displaystyle
\log x
logx
倍されてる"
\displaystyle
p^{m} ~ (m \geqq 2)
pm (m≧2)
←
の項は小さい
←
easy
\displaystyle
\updownarrow
↕
\displaystyle
\zeta (s)
ζ(s)
Riemann zeta
relation
(i) より,
\displaystyle
\sigma > 1
σ>1
に対し
\displaystyle
\left (\sigma - 1) \zeta (\sigma)\right)^{3} \left|\frac{\zeta (\sigma + it)}{\sigma - 1}\right|^{4} \biggl|\zeta (\sigma + 2 it)\biggr| \geqq \frac{1}{\sigma - 1}
(σ−1)ζ(σ))3∣∣∣∣σ−1ζ(σ+it)∣∣∣∣4∣∣∣∣ζ(σ+2it)∣∣∣∣≧σ−11
\displaystyle
\longrightarrow
⟶
\displaystyle
\sigma \to 1 + 0
σ→1+0
\displaystyle
\longrightarrow
⟶
\displaystyle
\sigma \to 1 + 0
σ→1+0
\displaystyle
\longrightarrow
⟶
\displaystyle
\sigma \to 1 + 0
σ→1+0
\displaystyle
\longrightarrow
⟶
\displaystyle
\sigma \to 1 + 0
σ→1+0
\displaystyle
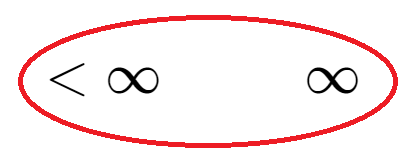
1
1
\displaystyle
\infty
∞
\displaystyle
\infty
∞
\displaystyle
< \infty
<∞
\displaystyle
\Longrightarrow
⟹
\displaystyle
\zeta (1 + it) \neq 0.
ζ(1+it)≠0.
\displaystyle
\longrightarrow
⟶
\displaystyle
\longleftarrow
⟵
\displaystyle
\bigcirc
◯